One of the most useful concepts for analysis that arise from topology and metric spaces is the concept of compactness; recall that a space is compact if every open cover of
has a finite subcover, or equivalently if any collection of closed sets with the finite intersection property (i.e. every finite subcollection of these sets has non-empty intersection) has non-empty intersection. In these notes, we explore how compactness interacts with other key topological concepts: the Hausdorff property, bases and sub-bases, product spaces, and equicontinuity, in particular establishing the useful Tychonoff and Arzelá-Ascoli theorems that give criteria for compactness (or precompactness).
Exercise 1 (Basic properties of compact sets)
- Show that any finite set is compact.
- Show that any finite union of compact subsets of a topological space is still compact.
- Show that any image of a compact space under a continuous map is still compact.
Show that these three statements continue to hold if “compact” is replaced by “sequentially compact”.
— 1. Compactness and the Hausdorff property —
Recall from Notes 8 that a topological space is Hausdorff if every distinct pair of points can be separated by two disjoint open neighbourhoods
of
respectively; every metric space is Hausdorff, but not every topological space is.
At first glance, the Hausdorff property bears no resemblance to the compactness property. However, they are in some sense “dual” to each other, as the following two exercises show:
Exercise 2 Let
be a compact topological space.
- Show that every closed subset in
is compact.
- Show that any weaker topology
on
also yields a compact topological space
.
- Show that the trivial topology on
is always compact.
Exercise 3 Let
be a Hausdorff topological space.
- Show that every compact subset of
is closed.
- Show that any stronger topology
on
also yields a Hausdorff topological space
.
- Show that the discrete topology on
is always Hausdorff.
The first exercise asserts that compact topologies tend to be weak, while the second exercise asserts that Hausdorff topologies tend to be strong. The next lemma asserts that the two concepts only barely overlap:
Lemma 1 Let
be a weak and strong topology respectively on a space
. If
is compact and
is Hausdorff, then
. (In other words, a compact topology cannot be strictly stronger than a Hausdorff one, and a Hausdorff topology cannot be strictly weaker than a compact one.)
Proof: Since , every set which is closed in
is closed in
, and every set which is compact in
is compact in
. But from Exercises 2, 3, every set which is closed in
is compact in
, and every set which is compact in
is closed in
. Putting all this together, we see that
and
have exactly the same closed sets, and thus have exactly the same open sets; in other words,
.
Corollary 2 Any continuous bijection
from a compact topological space
to a Hausdorff topological space
is a homeomorphism.
Proof: Consider the pullback of the topology on
by
; this is a topology on
. As
is continuous, this topology is weaker than
, and thus by Lemma 1 is equal to
. As
is a bijection, this implies that
is continuous, and the claim follows.
One may wish to compare this corollary with Corollary 2 from Notes 9.
Remark 1 Spaces which are both compact and Hausdorff (e.g. the unit interval
with the usual topology) have many nice properties and are moderately common, so much so that the two properties are often concatenated as CH. Spaces that are locally compact and Hausdorff (e.g. manifolds) are much more common and have nearly as many nice properties, and so these two properties are often concatenated as LCH. One should caution that (somewhat confusingly) in some older literature (particularly those in the French tradition), “compact” is used for “compact Hausdorff”.
(Optional) Another way to contrast compactness and the Hausdorff property is via the machinery of ultrafilters. Define an filter on a space to be a collection
of sets of
which is closed under finite intersection, is also monotone (i.e. if
and
, then
), and does not contain the empty set. Define an ultrafilter to be a filter with the additional property that for any
, exactly one of
and
lies in
. (See also this blog post of mine for more discussion of ultrafilters.)
Exercise 4 (Ultrafilter lemma) Show that every filter is contained in at least one ultrafilter. (Hint: use Zorn’s lemma, see Notes 7.)
Exercise 5 A collection of subsets of
has the finite intersection property if every finite intersection of sets in the collection has non-empty intersection. Show that every filter has the finite intersection property, and that every collection of sets with the finite intersection property is contained in a filter (and hence contained in an ultrafilter, by the ultrafilter lemma).
Given a point and an ultrafilter
on
, we say that
converges to
if every neighbourhood of
belongs to
.
Exercise 6 Show that a space
is Hausdorff if and only if every ultrafilter has at most one limit. (Hint: For the “if” part, observe that if
cannot be separated by disjoint neighbourhoods, then the neighbourhoods of
and
together enjoy the finite intersection property.)
Exercise 7 Show that a space
is compact if and only if every ultrafilter has at least one limit. (Hint: use the finite intersection property formulation of compactness and Exercise 5.)
— 2. Compactness and bases —
Compactness is the property that every open cover has a finite subcover. This property can be difficult to verify in practice, in part because the class of open sets is very large. However, in many cases one can replace the class of open sets with a much smaller class of sets. For instance, in metric spaces, a set is open if and only if it is the union of open balls (note that the union may be infinite or even uncountable). We can generalise this notion as follows:
Definition 3 (Base) Let
be a topological space. A base for this space is a collection
of open sets such that every open set in
can be expressed as the union of sets in the base. The elements of
are referred to as basic open sets.
Example 1 The collection of open balls
in a metric space forms a base for the topology of that space. As another (rather trivial) example of a base: any topology
is a base for itself.
This concept should be compared with that of a basis of a vector space: every vector in that space can be expressed as a linear combination of vectors in a basis. However, one difference between a base and a basis is that the representation of an open set as the union of basic open sets is almost certainly not unique.
Given a base , define a basic open neighbourhood of a point
to be a basic open set that contains
. Observe that a set
is open if and only if every point in
has a basic open neighbourhood contained in
.
Exercise 8 Let
be a collection of subsets of a set
. Show that
is a base for some topology
if and only if it it covers
and has the following additional property: given any
and any two basic open neighbourhoods
of
, there exists another basic open neighbourhood
of
that is contained in
. Furthermore, the topology
is uniquely determined by
.
To verify the compactness property, it suffices to do so for basic open covers (i.e. coverings of the whole space by basic open sets):
Exercise 9 Let
be a topological space with a base
. Then the following are equivalent:
- Every open cover has a finite subcover (i.e.
is compact);
- Every basic open cover has a finite subcover.
A useful fact about compact metric spaces is that they are in some sense “countably generated”.
Lemma 4 Let
be a compact metric space.
- (i)
is separable (i.e. it has an at most countably infinite dense subset).
- (ii)
is second-countable (i.e. it has an at most countably infinite base).
Proof: By Theorem 1 of Notes 8, is totally bounded. In particular, for every
, one can cover
by a finite number of balls
of radius
. The set of points
is then easily verified to be dense and at most countable, giving (i). Similarly, the set of balls
can be easily verified to be a base which is at most countable, giving (ii).
Remark 2 One can easily generalise compactness here to
-compactness; thus for instance finite-dimensional vector spaces
are separable and second-countable. The properties of separability and second-countability are much weaker than
-compactness in general, but can still serve to provide some constraint as to the “size” or “complexity” of a metric space or topological space in many situations.
We now weaken the notion of a base to that of a sub-base.
Definition 5 (Sub-base) Let
be a topological space. A sub-base for this space is a collection
of subsets of
such that
is the weakest topology that makes
open (i.e.
is generated by
). Elements of
are referred to as sub-basic open sets.
Observe for instance that every base is a sub-base. The converse is not true: for instance, the half-open intervals for
form a sub-base for the standard topology on
, but not a base. In contrast to bases, which need to obey the property in Exercise 8, no property is required on a collection
in order for it to be a sub-base; every collection of sets generates a unique topology with respect to which it is a sub-base.
The precise relationship between sub-bases and bases is given by the following exercise.
Exercise 10 Let
be a topological space, and let
be a collection of subsets of
. Then the following are equivalent:
is a sub-base for
.
- The space
of finite intersections of
(including the whole space
, which corresponds to the case
) is a base for
.
Thus a set is open iff it is the union of finite intersections of sub-basic open sets.
Many topological facts involving open sets can often be reduced to verifications on basic or sub-basic open sets, as the following exercise illustrates:
Exercise 11 Let
be a topological space, and
be a sub-base of
, and let
be a base of
.
- Show that a sequence
converges to a limit
if and only if every sub-basic open neighbourhood of
contains
for all sufficiently large
. (Optional: show that an analogous statement is also true for nets.)
- Show that a point
is adherent to a set
if and only if every basic open neighbourhood of
intersects
. Give an example to show that the claim fails for sub-basic open sets.
- Show that a point
is in the interior of a set
if and only if
contains a basic open neighbourhood of
. Give an example to show that the claim fails for sub-basic open sets.
- If
is another topological space, show that a map
is continuous if and only if the inverse image of every sub-basic open set is open.
There is a useful strengthening of Exercise 9 in the spirit of the above exercise, namely the Alexander sub-base theorem:
Theorem 6 (Alexander sub-base theorem) Let
be a topological space with a sub-base
. Then the following are equivalent:
- Every open cover has a finite subcover (i.e.
is compact);
- Every sub-basic open cover has a finite subcover.
Proof: Call an open cover bad if it had no finite subcover, and good otherwise. In view of Exercise 9, it suffices to show that if every sub-basic open cover is good, then every basic open cover is good also, where we use the basis coming from Exercise 10.
Suppose for contradiction that every sub-basic open cover was good, but at least one basic open cover was bad. If we order the bad basic open covers by set inclusion, observe that every chain of bad basic open covers has an upper bound that is also a bad basic open cover, namely the union of all the covers in the chain. Thus, by Zorn’s lemma, there exists a maximal bad basic open cover . Thus this cover has no finite subcover, but if one adds any new basic open set to this cover, then there must now be a finite subcover.
Pick a basic open set in this cover
. Then we can write
for some sub-basic open sets
. We claim that at least one of the
also lie in the cover
. To see this, suppose for contradiction that none of the
was in
. Then adding any of the
to
enlarges the basic open cover and thus creates a finite subcover; thus
together with finitely many sets from
cover
, or equivalently that one can cover
with finitely many sets from
. Thus one can also cover
with finitely many sets from
, and thus
itself can be covered by finitely many sets from
, a contradiction.
From the above discussion and the axiom of choice, we see that for each basic set in
there exists a sub-basic set
containing
that also lies in
. (Two different basic sets
could lead to the same sub-basic set
, but this will not concern us.) Since the
cover
, the
do also. By hypothesis, a finite number of
can cover
, and so
is good, which gives the desired a contradiction.
Exercise 12 (Optional) Use Exercise 7 to give another proof of the Alexander sub-base theorem.
Exercise 13 Use the Alexander sub-base theorem to show that the unit interval
(with the usual topology) is compact, without recourse to the Heine-Borel or Bolzano-Weierstrass theorems.
Exercise 14 Let
be a well-ordered set, endowed with the order topology (Exercise 9 of Notes 8); such a space is known as an ordinal space. Show that
is Hausdorff, and that
is compact if and only if
has a maximal element.
One of the major applications of the sub-base theorem is to prove Tychonoff’s theorem, which we turn to next.
— 3. Compactness and product spaces —
Given two topological spaces and
, we can form the product space
, using the cylinder sets
as a sub-base, or equivalently using the open boxes
as a base (cf. Example 15 from Notes 8). One easily verifies that the obvious projection maps
,
are continuous, and that these maps also provide homeomorphisms between
and
, or between
and
, for every
. Also observe that a sequence
(or net
) converges to a limit
in
if and only if
and
(or
and
) converge in
and
to
and
respectively.
This operation preserves a number of useful topological properties, for instance
Exercise 15 Prove that the product of two Hausdorff spaces is still Hausdorff.
Exercise 16 Prove that the product of two sequentially compact spaces is still sequentially compact.
Proposition 7 The product of two compact spaces is compact.
Proof: By Exercise 9 it suffices to show that any basic open cover of by boxes
has a finite subcover. For any
, this open cover covers
; by the compactness of
, we can thus cover
by a finite number of open boxes
. Intersecting the
together, we obtain a neighbourhood
of
such that
is covered by a finite number of these boxes. But by compactness of
, we can cover
by a finite number of
. Thus all of
can be covered by a finite number of boxes in the cover, and the claim follows.
Exercise 17 (Optional) Obtain an alternate proof of this proposition using Exercise 14 from Notes 8.
The above theory for products of two spaces extends without difficulty to products of finitely many spaces. Now we consider infinite products.
Definition 8 (Product spaces) Given a family
of topological spaces, let
be the Cartesian product, i.e. the space of tuples
with
for all
. For each
, we have the obvious projection map
that maps
to
.
- We define the product topology on
to be the topology generated by the cylinder sets
for
and
as a sub-base, or equivalently the weakest topology that makes all of the
continuous.
- We define the box topology on
to be the topology generated by all the boxes
, where
for all
.
Unless otherwise specified, we assume the product space to be endowed with the product topology rather than the box topology.
When is finite, the product topology and the box topology coincide. When
is infinite, the two topologies are usually different (as we shall see), but the box topology is always at least as strong as the product topology. Actually, in practice the box topology is too strong to be of much use – there are not enough convergent sequences in it. For instance, in the space
of real-valued sequences
, even sequences such as
do not converge to the zero sequence as
(why?), despite converging in just about every other sense.
Exercise 18 Show that the arbitrary product of Hausdorff spaces remains Hausdorff in either the product or the box topology.
Exercise 19 Let
be a sequence of metric spaces. Show that the the function
on the product space
defined by
is a metric on
which generates the product topology on
.
Exercise 20 Let
be a product space with the product topology. Show that a sequence
in that space converges to a limit
if and only if
converges in
to
for every
. (The same statement also holds for nets.) Thus convergence in the product topology is essentially the same concept as pointwise convergence (cf. Example 14 of Notes 8).
The box topology usually does not preserve compactness. For instance, one easily checks that the product of any number of discrete spaces is still discrete in the box topology. On the other hand, a discrete space is compact (or sequentially compact) if and only if it is finite. Thus the infinite product of any number of non-trivial (i.e. having at least two elements) compact discrete spaces will be non-compact, and similarly for sequential compactness.
The situation improves significantly with the product topology, however (which is weaker, and thus more likely to be compact). We begin with the situation for sequential compactness.
Proposition 9 (Sequential Tychonoff theorem) Any at most countable product of sequentially compact topological spaces is sequentially compact.
Proof: We will use the “Arzelá-Ascoli diagonalisation argument”. The finite case is already handled by Exercise 16 (and can in any event be easily deduced from the countable case), so suppose we have a countably infinite sequence of sequentially compact spaces, and consider the product space
with the product topology. Let
be a sequence in
, thus each
is itself a sequence
with
for all
. Our objective is to find a subsequence
which converges to some limit
in the product topology, which by Exercise 20 is the same as pointwise convergence (i.e.
as
for each
).
Consider the first coordinates of the sequence
. As
is sequentially compact, we can find a subsequence
in
such that
converges in
to some limit
.
Now, in this subsequence, consider the second coordinates . As
is sequentially compact, we can find a further subsequence
in
such that
converges in
to some limit
. Also, we inherit from the preceding subsequence that
converges in
to
.
We continue in this vein, creating nested subsequences for
whose first
components
converge to
respectively.
None of these subsequences, by themselves are sufficient to finish the problem. But now we use the diagonalisation trick: we consider the diagonal sequence . One easily verifies that
converges in
to
as
for every
, and so we have extracted a sequence that is convergent in the product topology.
Remark 3 In the converse direction, if a product of spaces is sequentially compact, then each of the factor spaces must also be sequentially compact, since they are continuous images of the product space and one can apply Exercise 1.
The sequential Tychonoff theorem breaks down for uncountable products. Consider for instance the product space of functions
. As
(with the discrete topology) is sequentially compact, this is an (uncountable) product of sequentially compact spaces. On the other hand, for each
we can define the evaluation function
by
. This is a sequence in
; we claim that it has no convergent subsequence. Indeed, given any
, we can find
such that
does not converge to a limit as
, and so
does not converge pointwise (i.e. does not converge in the product topology).
However, we can recover the result for uncountable products as long as we work with topological compactness rather than sequential compactness, leading to Tychonoff’s theorem:
Theorem 10 (Tychonoff theorem) Any product of compact topological spaces is compact.
Proof: Write for this product of compact topological spaces. By Theorem 6, it suffices to show that any open cover of
by sub-basic open sets
has a finite sub-cover, where
is some index set, and for each
,
and
is open in
.
For each , consider the sub-basic open sets
that are associated to those
with
. If the open sets
here cover
, then by compactness of
, a finite number of the
already suffice to cover
, and so a finite number of the
cover
, and we are done. So we may assume that the
do not cover
, thus there exists
that avoids all the
with
. One then sees that the point
in
avoids all of the
, a contradiction. The claim follows.
Remark 4 The axiom of choice was used in several places in the proof (in particular, via the Alexander sub-base theorem). This turns out to be necessary, because one can use Tychonoff’s theorem to establish the axiom of choice. This was first observed by Kelley, and can be sketched as follows. It suffices to show that the product
of non-empty sets is again non-empty. We can make each
compact (e.g. by using the trivial topology). We then adjoin an isolated element
to each
to obtain another compact space
, with
closed in
. By Tychonoff’s theorem, the product
is compact, and thus every collection of closed sets with finite intersection property has non-empty intersection. But observe that the sets
in
, where
is the obvious projection, are closed and has the finite intersection property; thus the intersection of all of these sets is non-empty, and the claim follows.
Remark 5 From the above discussion, we see that the space
is compact but not sequentially compact; thus compactness does not necessarily imply sequential compactness.
Exercise 21 Let us call a topological space
first-countable if, for every
, there exists a countable family
of open neighbourhoods of
such that every neighbourhood of
contains at least one of the
.
- Show that every metric space is first-countable.
- Show that every second-countable space is first-countable (see Lemma 4).
- Show that every separable metric space is second-countable.
- Show that every space which is second-countable, is separable.
- Show that any compact space which is first-countable, is also sequentially compact. (The converse is not true: Exercise 9 from Notes 8 provides a counterexample.)
(Optional) There is an alternate proof of the Tychonoff theorem that uses the machinery of universal nets. We sketch this approach in a series of exercises.
Definition 11 A net
in a set
is universal if for every function
, the net
converges to either
or
.
Exercise 22 Show that a universal net
in a compact topological space is necessarily convergent. (Hint: show that the collection of closed sets which contain
for sufficiently large
enjoys the finite intersection property.)
Exercise 23 (Kelley’s theorem) Every net
in a set
has a universal subnet
. (Hint: First use Exercise 5 to find an ultrafilter
on
that contains the upsets
for all
. Now let
be the space of all pairs
, where
, ordered by requiring
when
and
, and let
be the map
.)
Exercise 24 Use the previous two exercises, together with Exercise 20, to establish an alternate proof of Tychonoff’s theorem.
Exercise 25 Establish yet another proof of Tychonoff’s theorem using Exercise 7 directly (rather than proceeding via Exercise 12).
— 4. Compactness and equicontinuity —
We now pause to give an important application of the (sequential) Tychonoff theorem. We begin with some definitions. If is a topological space and
is a metric space, let
be the space of bounded continuous functions from
to
. (If
is compact, this is the same space as
, the space of continuous functions from
to
.) We can give this space the uniform metric
Exercise 26 If
is complete, show that
is a complete metric space. (Note that this implies Exercise 2 from Notes 6.)
Note that if is continuous if and only if, for every
and
, there exists a neighbourhood
of
such that
for all
. We now generalise this concept to families.
Definition 12 Let
be a topological space, let
be a metric space, and Let
be a family of functions
.
- We say that this family
is pointwise bounded if for every
, the set
is bounded in
.
- We say that this family
is pointwise precompact if for every
, the set
is precompact in
.
- We say that this family
is equicontinuous if for every
and
, there exists a neighbourhood
of
such that
for all
and
.
- If
is also a metric space, we say that the family
is uniformly equicontinuous if for every
there exists a
such that
for all
and
with
.
Remark 6 From the Heine-Borel theorem, the pointwise boundedness and pointwise precompactness properties are equivalent if
is a subset of
for some
. Any finite collection of continuous functions is automatically an equicontinuous family (why?), and any finite collection of uniformly continuous functions is automatically a uniformly equicontinuous family; the concept only acquires additional meaning once one considers infinite families of continuous functions.
Example 2 With
and
, the family of functions
for
are pointwise bounded (and thus pointwise precompact), but not equicontinuous. The family of functions
for
, on the other hand, are equicontinuous, but not pointwise bounded or pointwise precompact. The family of functions
for
are pointwise bounded (even uniformly bounded), but not equicontinuous.
Example 3 With
and
, the functions
are pointwise bounded (even uniformly bounded), are equicontinuous, and are each individually uniformly continuous, but are not uniformly equicontinuous.
Exercise 27 Show that the uniform boundedness principle (Theorem 2 from Notes 9) can be restated as the assertion that any family of bounded linear operators from the unit ball of a Banach space to a normed vector space is pointwise bounded if and only if it is equicontinuous.
Example 4 A function
between two metric spaces is said to be Lipschitz (or Lipschitz continuous) if there exists a constant
such that
for all
; the smallest constant
one can take here is known as the Lipschitz constant of
. Observe that Lipschitz functions are automatically continuous, hence the name. Also observe that a family
of Lipschitz functions with uniformly bounded Lipschitz constant is equicontinuous.
One nice consequence of equicontinuity is that it equates uniform convergence with pointwise convergence, or even pointwise convergence on a dense subset.
Exercise 28 Let
be a topological space, let
be a complete metric space, let
be an equicontinuous family of functions. Show that the following are equivalent:
- The sequence
is pointwise convergent.
- The sequence
is pointwise convergent on some dense subset of
.
If
is compact, show that the above two statements are also equivalent to
- The sequence
is uniformly convergent.
(Compare with Corollary 1 from Notes 9.) Show that no two of the three statements remain equivalent if the hypothesis of equicontinuity is dropped.
We can now use Proposition 9 to give a useful characterisation of precompactness in when
is compact, known as the Arzelá-Ascoli theorem:
Theorem 13 (Arzelá-Ascoli theorem) Let
be a metric space,
be a compact metric space, and let
be a family of functions
. Then the following are equivalent:
- (i)
is a precompact subset of
.
- (ii)
is pointwise precompact and equicontinuous.
- (iii)
is pointwise precompact and uniformly equicontinuous.
Proof: We first show that (i) implies (ii). For any , the evaluation map
is a continuous map from
to
, and thus maps precompact sets to precompact sets. As a consequence, any precompact family in
is pointwise precompact. To show equicontinuity, suppose for contradiction that equicontinuity failed at some point
, thus there exists
, a sequence
, and points
such that
for every
. One then verifies that no subsequence of
can converge uniformly to a continuous limit, contradicting precompactness. (Note that in the metric space
, precompactness is equivalent to sequential precompactness.)
Now we show that (ii) implies (iii). It suffices to show that equicontinuity implies uniform equicontinuity. This is a straightforward generalisation of the more familiar argument that continuity implies uniform continuity on a compact domain, and we repeat it here. Namely, fix . For every
, equicontinuity provides a
such that
whenever
and
. The balls
cover
, thus by compactness some finite subcollection
,
of these balls cover
. One then easily verifies that
whenever
with
.
Finally, we show that (iii) implies (i). It suffices to show that any sequence ,
, which is pointwise precompact and uniformly equicontinuous, has a convergent subsequence. By embedding
in its metric completion
, we may assume without loss of generality that
is complete. (Note that for every
, the set
is precompact in
, hence the closure in
is complete and thus closed in
also. Thus any pointwise limit of the
in
will take values in
.) By Lemma 4, we can find a countable dense subset
of
. For each
, we can use pointwise precompactness to find a compact set
such that the
take values in
. For each
, the tuple
can then be viewed as a point in the product space
. By Proposition 9, this product space is sequentially compact, hence we may find a subsequence
such that
is convergent in the product topology, or equivalently that
pointwise converges on the countable dense set
. The claim now follows from Exercise 28.
Remark 7 The above theorem characterises precompact subsets of
when
is a compact metric space. One can also characterise compact subsets by observing that a subset of a metric space is compact if and only if it is both precompact and closed.
There are many variants of the Arzelá-Ascoli theorem with stronger or weaker hypotheses or conclusions; for instance, we have
Corollary 14 (Arzelá-Ascoli theorem, special case) Let
be a sequence of functions from a compact metric space
to a finite-dimensional vector space
which are equicontinuous and pointwise bounded. Then there is a subsequence
of
which converges uniformly to a limit (which is necessarily bounded and continuous).
Thus, for instance, any sequence of uniformly bounded and uniformly Lipschitz functions will have a uniformly convergent subsequence. This claim fails without the uniform Lipschitz assumption (consider, for instance, the functions
). Thus one needs a “little bit extra” uniform regularity in addition to uniform boundedness in order to force the existence of uniformly convergent subsequences. This is a general phenomenon in infinite-dimensional function spaces: compactness in a strong topology tends to require some sort of uniform control on regularity or decay in addition to uniform bounds on the norm.
Exercise 29 Show that the equivalence of (i) and (ii) continues to hold if
is assumed to be just a compact Hausdorff space rather than a compact metric space (the statement (iii) no longer makes sense in this setting). Hint:
need not be separable any more, however one can still adapt the diagonalisation argument used to prove Proposition 9. The starting point is the observation that for every
and every
, one can find a neighbourhood
of
and some subsequence
which only oscillates by at most
(or maybe
) on
.
Exercise 30 (Locally compact Hausdorff version of Arzelá-Ascoli) Let
be a locally compact Hausdorff space which is also
-compact, and let
be an equicontinuous, pointwise bounded sequence of functions. Then there exists a subsequence
which converges uniformly on compact subsets of
to a limit
. (Hint: Express
as a countable union of compact sets
, each one contained in the interior of the next. Apply the compact Hausdorff Arzelá-Ascoli theorem on each compact set (Exercise 29). Then apply the Arzelá-Ascoli argument one last time.)
Remark 8 The Arzelá-Ascoli theorem (and other compactness theorems of this type) are often used in partial differential equations, to demonstrate existence of solutions to various equations or variational problems. For instance, one may wish to solve some equation
, for some function
. One way to do this is to first construct a sequence
of approximate solutions, so that
as
in some suitable sense. If one can also arrange these
to be equicontinuous and pointwise bounded, then the Arzelá-Ascoli theorem allows one to pass to a subsequence that converges to a limit
. Given enough continuity (or semi-continuity) properties on
, one can then show that
as required.
More generally, the use of compactness theorems to demonstrate existence of solutions in PDE is known as the compactness method. It is applicable in a remarkably broad range of PDE problems, but often has the drawback that it is difficult to establish uniqueness of the solutions created by this method (compactness guarantees existence of a limit point, but not uniqueness). Also, in many cases one can only hope for compactness in rather weak topologies, and as a consequence it is often difficult to establish regularity of the solutions obtained via compactness methods.
[Update, Feb 20: some corrections, new exercise added (note renumbering).]

61 comments
Comments feed for this article
22 January, 2023 at 6:44 am
Anonymous
Below Remark 3:
we can find
–>
we can find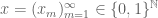
At the end of Definition 12:
and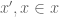 with
with  .
.
–>
and with
with  .
.
[Corrected, thanks – T.]
22 January, 2023 at 6:48 am
Anonymous
Regarding Definition 12, can one still define the notion of “uniform equicontinuity” when is merely a topological space?
is merely a topological space?
Does the following definition make sense?
We say that this family is “uniformly equicontinuous” (or “equi-uniformly-continuous”) if for every
is “uniformly equicontinuous” (or “equi-uniformly-continuous”) if for every  , there exists an open set
, there exists an open set  such that
such that  for all
for all  and
and  .
.
26 January, 2023 at 5:22 pm
Terence Tao
This is not an interesting notion (one could take to be the empty set, for instance). In order to have a good notion of uniform continuity (or equicontinuity), one needs the structure of a uniform space.
to be the empty set, for instance). In order to have a good notion of uniform continuity (or equicontinuity), one needs the structure of a uniform space.
22 January, 2023 at 12:11 pm
Anonymous
Some pedantic comments:
1. In the proof of “(iii) implies (i)” in Theorem 13,
For each
… is clearer
is clearer
2. Possible typos in
hence we may find a subsequence
which seems to be:
hence we may find a subsequence such that
such that 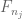 is convergent in the product topology, or equivalently that
is convergent in the product topology, or equivalently that  pointwise
pointwise
3.
The subscripts and
and  are used in the proof. While it is clear that a sequence “
are used in the proof. While it is clear that a sequence “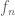 ” can be clearly understood as
” can be clearly understood as  , the following in the proof:
, the following in the proof:
… such that
means
… such that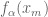 ,
, 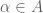 take values in
take values in  .
.
not
… such that ,
,  take values in
take values in  .
.
23 January, 2023 at 6:25 am
Anonymous
In the proof of “(iii) implies (i)” in Theorem 13:
Note that for every
1. I may miss something obvious. Why “any pointwise limit of the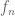 in
in  will take values in
will take values in 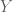 “? One only knows from the quoted argument that the closure in
“? One only knows from the quoted argument that the closure in 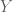 is closed in
is closed in  , which means the limit should take values in
, which means the limit should take values in  ?
?
2. “hence the closure in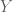 is complete and thus closed in
is complete and thus closed in  also” What is the use of completeness here? Is the closure in
also” What is the use of completeness here? Is the closure in 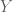 not automatically closed in
not automatically closed in  ?
?
26 January, 2023 at 6:08 pm
Terence Tao
1. Yes. If is a limit of the
is a limit of the  in
in  , then it will lie in the Y-closure of the
, then it will lie in the Y-closure of the  since this is already closed in
since this is already closed in  .
.
2. No. For instance,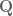 is closed in
is closed in 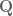 , but is not closed in
, but is not closed in 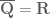 . However, any complete subset of
. However, any complete subset of 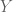 will be closed in
will be closed in  ; this is a good exercise for you to prove.
; this is a good exercise for you to prove.