Recently, I have been studying the concept of amenability on groups. This concept can be defined in a “combinatorial” or “finitary” fashion, using Følner sequences, and also in a more “functional-analytic” or “infinitary”‘ fashion, using invariant means. I wanted to get some practice passing back and forth between these two definitions, so I wrote down some notes on how to do this, and also how to take some facts about amenability that are usually proven in one setting, and prove them instead in the other. These notes are thus mostly for my own benefit, but I thought I might post them here also, in case anyone else is interested.
— 1. Equivalent definitions of amenability —
For simplicity I will restrict attention to countable groups . Given any
and
, I define the left-translation
by the formula
. Given
as well, I define the inner product
whenever the right-hand side is convergent.
All spaces are real-valued. The cardinality of a finite set
is denoted
. The symmetric difference of two sets
is denoted
.
A finite mean is a non-negative, finitely supported function such that
. A mean is a non-negative linear functional
such that
. Note that every finite mean
can be viewed as a mean
by the formula
.
The following equivalences were established by Følner:
Theorem 1 Let
be a countable group. Then the following are equivalent:
- (i) There exists a left-invariant mean
, i.e. mean such that
for all
and
.
- (ii) For every finite set
and every
, there exists a finite mean
such that
for all
.
- (iii) For every finite set
and every
, there exists a non-empty finite set
such that
for all
.
- (iv) There exists a sequence
of non-empty finite sets such that
as
for each
. (Such a sequence is called a Følner sequence.)
Proof: We shall use an argument of Namioka.
(i) implies (ii): Suppose for contradiction that (ii) failed, then there exists such that
for all means
. The set
is then a convex set of
that is bounded away from zero. Applying the Hahn-Banach separation theorem, there thus exists a linear functional
such that
for all means
. Since
, there thus exist
for
such that
for all means
, thus
. Specialising
to the Kronecker means
we see that
pointwise. Applying the mean
, we conclude that
. But this contradicts the left-invariance of
.
(ii) implies (iii): Fix (which we can take to be non-empty), and let
be a small quantity to be chosen later. By (ii) we can find a finite mean
such that
for all .
Using the layer-cake decomposition, we can write for some nested non-empty sets
and some positive constants
. As
is a mean, we have
. On the other hand, observe that
is at least
on
. We conclude that
for all , and thus
By the pigeonhole principle, there thus exists such that
and the claim follows.
(iii) implies (iv): Write the countable group as the increasing union of finite sets
and apply (iii) with
and
to create the set
.
(iv) implies (i): Use the Hahn-Banach theorem to select an infinite mean , and define
. (Alternatively, one can define
to be an ultralimit of the
.)
Any countable group obeying any (and hence all) of (i)-(iv) is called amenable.
Remark 1 The above equivalences are proven in a non-constructive manner, due to the use of the Hahn-Banach theorem (as well as the contradiction argument). Thus, for instance, it is not immediately obvious how to convert an invariant mean into a Følner sequence, despite the above equivalences.
— 2. Examples of amenable groups —
We give some model examples of amenable and non-amenable groups:
Proof: Trivial (either using invariant means or Følner sequences).
Proof: One can take the sets as the Følner sequence, or an ultralimit as an invariant mean.
Proposition 4 The free group
on two generators
is not amenable.
Proof: We first argue using invariant means. Suppose for contradiction that one had an invariant mean . Let
be the set of all words beginning with
,
,
respectively. Observe that
, thus
. By invariance we conclude that
; similarly for
,
,
. Since the identity element clearly must have mean zero, we conclude that the mean
is identically zero, which is absurd.
Now we argue using Følner sequences. If were amenable, then for any
we could find a finite non-empty set
such that
differs from
by at most
points for
. The set
is contained in
and in
, and so
and thus
Similarly for permutations. Summing up over all four permutations, we obtain
leading to a contradiction for small enough (any
will do).
Remark 2 The non-amenability of the free group is related to the Banach-Tarski paradox (see my earlier lecture notes on this).
Now we generate some more amenable groups.
Proposition 5 Let
be a short exact sequence of countable groups (thus
can be identified with a normal subgroup of
, and
can be identified with
). If
and
are amenable, then
is amenable also.
Proof: Using invariant means, there is a very short proof: given invariant means ,
for
, we can build an invariant mean
for
by the formula
for any , where
is the function defined as
for all cosets
(note that the left-invariance of
shows that the exact choice of coset representative
is irrelevant). (One can view
as sort of a “product measure” of the
and
.)
Now we argue using Følner sequences instead. Let ,
be Følner sequences for
respectively. Let
be a finite subset of
, and let
. We would like to find a finite non-empty subset
such that
for all
; this will demonstrate amenability. (Note that by taking
to be symmetric, we can replace
with
without difficulty.)
By taking large enough, we can find
such that
differs from
by at most
elements for all
, where
is the projection map. Now, let
be a preimage of
in
. Let
be the set of all group elements
such that
intersects
. Observe that
is finite. Thus, by taking
large enough, we can find
such that
differs from
by at most
points for all
.
Now set . Observe that the sets
for
lie in disjoint cosets of
and so
. Now take
, and consider an element of
. This element must take the form
for some
and
. The coset of
that
lies in is given by
. Suppose first that
lies outside of
. By construction, this occurs for at most
choices of
, leading to at most
elements in
.
Now suppose instead that lies in
. Then we have
for some
and
, by construction of
, and so
. But as
lies outside of
,
must lie outside of
. But by construction of
, there are at most
possible choices of
that do this for each fixed
, leading to at most
. We thus have
as required.
Proposition 6 Let
be a sequence of countable amenable groups. Then
is amenable.
Proof: We first use invariant means. An invariant mean on induces a mean on
which is invariant with respect to translations by
. Taking an ultralimit of these means, we obtain the claim.
Now we use Følner sequences. Given any finite set and
, we have
for some
. As
is amenable, we can find
such that
for all
, and the claim follows.
Proposition 7 Every countable virtually solvable group
is amenable.
Proof: Every virtually solvable group contains a solvable group of finite index, and thus contains a normal solvable subgroup of finite index. (Note that every subgroup of
of index
contains a normal subgroup of index at most
, namely the stabiliser of the
action on
.) By Proposition 5 and Proposition 2, we may thus reduce to the case when
is solvable. By inducting on the derived length of this solvable group using Proposition 5 again, it suffices to verify this when the group is abelian. By Proposition 6, it suffices to verify this when the group is abelian and finitely generated. By Proposition 5 again, it suffices to verify this when the group is cyclic. But this follows from Proposition 2 and Proposition 3.

33 comments
Comments feed for this article
15 April, 2009 at 3:46 pm
Anon
In Theorem 1.iii, should that K be a G? [Corrected, thanks – T.]
16 April, 2009 at 4:12 am
Spencer
Hello,
I’d never heard of amenability before coming across it on this blog and to the uninitiated it feels like a strange definition. Most of the theorems are of the form “If X holds then G is amenable” or “If H,K etc are amenable then G is amenable”. Are there results which *use* amenability in a positive way? – like a problem which was otherwise confusing but now we can say “Aha! This is trivial because G is clearly amenable” or suchlike.
This may be asking too much but I suppose what I’m really saying is: If one were trying to convince someone that amenability is a worthwhile concept and the ‘right’ definition of a more intuitive idea then what would one say?
Spencer
16 April, 2009 at 5:08 am
John Armstrong
Spencer: I’ve never really heard of amenability before either, but here are my thoughts off-the-cuff. There are two sides to this definition, as Dr. Tao is emphasizing.
First is the existence of an invariant structure on the group. I can see glimmers of why a mean in particular would be useful, but just the existence of invariant structures is nice. From my more geometric perspective, I’m drawn to the example of having a left-invariant measure on a Lie group.
Second is the combinatorial side, which I think can be summarized as follows. If you give me any finite collection of group elements to act on the group, then I can give you a finite collection of points such that your translations send most of them back into the collection. That is, no matter what bunch of movements you’re allowed to use, I can find a place in the group that’s more or less stable.
The really interesting part is, of course, that these two conditions are actually equivalent, despite how different they look on the surface. What Dr. Tao is trying to do is to push this equivalence deeper. Some applications of amenability suggest using the first property, while others suggest using the second. But since they’re both equivalent, it should be possible to use either property to prove either collection of applications.
16 April, 2009 at 6:52 am
Danny Calegari
One typical application is to dynamics. For example, it is a very useful fact that a homeomorphism of a compact topological space preserves an invariant probability measure. One way to construct such a measure is as follows. The homeomorphism f in question generates an action of the group Z of integers on the metric space (by taking powers, inverses of powers, etc.). Fix a point p in the space, and for every finite subset S of the integers, consider the probability measure mu_S which counts the points f^n(p) with n in S with equal weight. If S is the set of integers between -n and n for some big n, the probability measure mu_S is “almost invariant” under f. A weak limit of such measures associated to a Folner sequence in Z is actually invariant under the action of Z.
This fact generalizes to amenable groups in a straightforward way: if an amenable group G acts on a compact topological space, fix a point p in the space, and for every finite subset S of G, associate a probability measure mu_S on the space in more-or-less the same way. Again, a weak limit of measures associated to a Folner sequence is invariant.
You can then ask the question of why one cares about invariant measures, or indeed about dynamics . . .
16 April, 2009 at 7:20 am
Danny Calegari
Here’s another example, probably of no interest to anyone who is not already aware of it. In any group G, the commutator subgroup G’ is the subgroup generated by commutators (i.e. expressions of the form ghg^{-1}h^{-1} where g and h are in G). For every element g in G’, define the commutator length of g to be the smallest number of commutators in G whose product is equal to g. You can then define the stable commutator length of an element g in G’ to be the following limit: stable commutator length of g = lim_{n \to \infty} (commutator length of g^n) divided by n. A non-obvious fact is that if G is amenable, the stable commutator length of every element of G’ is zero. By constrast, in a free group, the stable commutator length of every (nontrivial) element is at least 1/2.
This is one of the algebraic tips of a big iceberg; a slightly more technical statement is that if G is an amenable group, the (real) bounded cohomology of G vanishes.
Since I brought it up, I might as well refer you to an expository note I wrote for the Notices at http://www.ams.org/notices/200809/tx080901100p.pdf
16 April, 2009 at 9:49 am
Terence Tao
The original motivation of amenability, I believe, came from trying to understand the Banach-Tarski paradox: how a ball in three dimensions can be cut up and reassembled to create, say, two balls of the same size as the original. This paradoxical decomposition is possible in three and higher dimensions but not in one or two dimensions; to oversimplify massively, this is because the group of rotations is basically amenable in one and two dimensions but not amenable in higher dimensions. I discuss this a bit in my post
As Danny says, one of the main benefits of amenability of a group G is that it allows one to take asymptotic averages over G, which brings the powerful tools of ergodic theory and dynamical systems into play to create all sorts of nice asymptotic invariants. More generally, I think that the representation theory of infinite groups is quite sensitive to whether the group is amenable or not, though I am not an expert in these matters.
16 April, 2009 at 11:16 am
Brian Forrest
The notion of amenability has a natural extension to locally compact groups. Here the interplay between the topology and the group structure is significant. For example there are compact Lie groups that are amenable as locally compact groups (all compact groups have this property), but are not amenable in the discrete topology because they contain a copy of the free group on two generators.
The heory of amenable groups (both locally compact and discrete) is massive. There are literally hundreds of properties that are implied by amenability, imply amanability or are equivalent to amenability. There are also numerous fundamental generalizations of concept to many other mathematical objects. Overall, the concept plays an important role in many diverse branches of mathematics.
A very good reference is A. Paterson’s book “Amenability”.
16 April, 2009 at 3:02 pm
Spencer
Thanks Danny, John, Terry and Brian. Very helpful comments.
20 April, 2009 at 12:26 pm
Jason Behrstock
The following gives a nice geometric/financial criterion for non-amenability of finitely generated groups. For a proof see chapter 6 of Gromov’s book on Metric Structures for Riemannian and Non-Riemannian Spaces.
Suppose that at each vertex of the Cayley graph of a finitely generated group G is a person holding a dollar. At a given time everybody is told to pass their dollar bill to a neighbor who lives within a uniformly fixed distance (this bound depends only on the group G and the choice of generating set). This can be done so that each person’s net worth increases if and only if the group G is non-amenable. Thus, one can think of non-amenable groups as those where Ponzi schemes can benefit everyone.
This criterion can be used, for instance, to give a simple proof of Proposition 4 above: the Cayley graph of the free group with respect to the natural choice of generators is an infinite 4-valent tree, if everyone passes their dollar towards the origin then everyone’s net worth increases. (Iterate to get rich!)
20 April, 2009 at 2:19 pm
Terence Tao
Dear Jason,
This is indeed an amusing interpretation of non-amenability. It seems related to another characterisation I know of, namely that a group is non-amenable if and only if its Cayley graph supports non-trivial bounded harmonic functions (i.e. if Liouville’s theorem fails for the group).
Very roughly speaking, it seems that amenable groups are the ones which can be “approximated by finite groups” (or by finite group-like objects), whereas non-amenable groups are those which are genuinely inapproximable by finitary objects. Thus the latter groups tend to exhibit all sorts of nasty behaviour that one doesn’t see in the finitary world (e.g. Ponzi schemes that actually work!)
21 April, 2009 at 12:26 am
Danny Calegari
Hi Terry – I’m confused by your last comment. I seem to remember that it’s a theorem of Kaimanovich and Vershik that for any amenable group G there is *some* symmetric nondegenerate (i.e. generating G as a semigroup) probability measure for which the Poisson boundary is trivial (i.e. there are no nontrivial bounded harmonic functions) – I think this was a conjecture of Furstenburg. But I think there are examples (some due to Kaimanovich-Vershik?, some to Erschler? and others??) of amenable groups for which other symmetric nondegenerate measures – even measures of finite support – do have nontrivial Poisson boundary. In fact, didn’t Erschler construct a compact Riemannian manifold with amenable fundamental group whose universal cover admits lots of bounded harmonic functions?
21 April, 2009 at 8:23 am
Anders Karlsson
Danny is right. Many finitely generated amenable groups (especially those of exponential growth) do have nontrivial bounded harmonic functions w.r.t certain probability measures, even symmetric and finitely supported ones. Perhaps the simplest examples to see this are solvable so-called wreath products or Lamplighter groups, for more details see for example Kaimanovich-Vershik
http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.aop/1176993497
page 480.
Think of the lattice Z^d with lamps at each vertex.
The group G can be thought of Z^d (the position of the lamplighter) and finite sets of vertices of Z^d (=lamps switched on). (The group operation is the natural one; the lamps are Z/2Z). Consider the simple symmetric random walk of a “lamplighter” on Z^d. If d is at least 3 this random walk is transient. He may switch on/off the lamp where he stands. For d at least 3 this means that the lamp configuration eventually stabilize in each finite region. So the function assigning to a starting postition of the lamplighter and finite lamp configuration, the probability that the lamp at (for example) the origin of Z^d eventually remains switched on, is a nontrivial bounded harmonic function on G. For d=1 or 2 the same can be achieved with asymmetric measure. (BTW, it is known that when d=1 the corresponding standard Cayley graph is the simplest Diestel-Leader graph.)
Note that this is in a sense a discrete phenomenon: it is known that for symmetric probability measures absolutely continuous w.r.t Haar on an amenable Lie group, every bounded harmonic function is constant. For more information I recommend Erschler http://www.springerlink.com/content/qxmjna69xe8v67un/
21 April, 2009 at 9:55 am
Terence Tao
Dear Danny and Anders, thanks for the correction! I didn’t realise the subtlety involving the choice of symmetric measure. (As mentioned in the main post, I’m still in the process of understanding amenability!) So to summarise:
For non-amenable groups, one has non-constant bounded harmonic functions for any choice of symmetric measure;
For amenable groups, there are symmetric measures for which all bounded harmonic functions are constant, but (at least in the discrete case) there can exist symmetric measures with respect to which non-constant bounded harmonic functions exist.
24 April, 2009 at 10:02 pm
Orr
Hi,
In Theorem 1, ii implies iii, I think an epsilon is missing from the last two equations.
[Corrected, thanks – T.]
25 April, 2009 at 9:17 am
A Problem on Planar Percolation « Combinatorics and more
[…] proof by Itai, Russ, Yuval, and Oded of the “dying percolation property” for nonamenable groups was outlined. And the Burton-Keane beautiful result on unique infinite connected […]
23 May, 2009 at 12:22 am
adebayo emmanuel
I am really interested in the article and even the topic at large.
20 July, 2009 at 2:18 pm
Gábor Pete
I think it’s worth adding to the discussion on non-constant bounded harmonic functions that for many amenable groups (e.g., the lamplighter group over Z^3), the only known symmetric measures with no such functions have UNBOUNDED support. In fact, it is a well-known question whether the Liouville property of a group is independent of the finite generating set taken. On the other hand, it is known to be NOT a quasi-isometry invariant property of graphs and Riemannian manifolds (T. Lyons 1987 and I. Benjamini 1991).
The failure of Liouville property is interesting for many reasons, e.g., it is equivalent to having positive speed and positive entropy for the random walk with steps given by that measure.
From the point of view of random walks, it is quite counterintuitive at first glance that a symmetric measure with unbounded jumps can be slower than any (or at least, any natural) walk with symmetric bounded jumps on the same group. But in the usual construction, those unbounded jumps are supported on large Folner sets, so it’s not really that surprising.
22 August, 2009 at 9:06 pm
excuses, excuses « Since it is not …
[…] sometimes it allows quicker/slicker proofs of certain results (for instance, see Prop. 5 in these expository notes by Terence Tao). So, I thought it might be worth a post looking at amenability from the function-space […]
23 January, 2010 at 12:15 am
Some notes on group extensions « What’s new
[…] results in group theory in a succinct form using this notation. For instance, one of the results in my earlier blog post on amenability now states that amenable-by-amenable groups are amenable. Another example that I have been looking […]
19 March, 2010 at 9:54 pm
A computational perspective on set theory « What’s new
[…] low and high dimensional cases is that the free group is not amenable, whereas is amenable. See these previous blog posts for further discussion.) Possibly related posts: (automatically generated)The “no […]
2 January, 2012 at 3:29 am
Robert Treger
Consider a projective manifold X with large, residually finite, and a non-amenable fundamental group. Let U denote its universal covering. It is known that U has infinitely many bounded harmonic functions. Do those functions separate points on U provided U is Stein?
13 July, 2012 at 10:22 am
dasziggy
In Theorem 1, (i) ==> (ii), shouldn’t the negation of (ii) be:
“There exists {S, \epsilon} s.t. for all means {\nu} there \textbf{exists} {x \in S} such that {\| \nu – \tau_x \nu\|_{\ell^1(G)} > \epsilon} .”
[Corrected, thanks – T.]
23 January, 2013 at 2:49 am
First Bourbaki seminar of 2013 « Disquisitiones Mathematicae
[…] For more details on these properties (in the case of countable groups), the reader might want to consult Terence Tao’s notes on this subject. […]
9 March, 2013 at 12:19 am
Mustafa Said
There is a good set of notes on “Amenability for von Neumann Algebras, Hyperfiniteness” by Remi Boutonnet
23 September, 2016 at 2:15 am
S.
Nice. I have a question about the conditions (iii) and (iv) in Theorem 1:, is there a possibility to prove the equivalence of both conditions without using that is countable?
is countable?
11 May, 2017 at 3:25 pm
Generalisations of the limit functional | What's new
[…] can be viewed as a demonstration of the amenability of the natural numbers (or integers); see this previous blog post for further […]
17 January, 2021 at 1:16 pm
DHan
I think in theorem 1, the part from (ii) to (iii), the first inequality is not very clear from the observation. I prefer Namioka’s proof for this. But anyway, many thanks for this post!
18 September, 2023 at 3:42 am
Anonymous
in prop5, if H is uncountable ,why preimage of F_{n} is finite?
18 September, 2023 at 8:19 am
Terence Tao
We select one preimage of each element of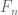 to create
to create  , so
, so  will have the same cardinality as
will have the same cardinality as 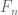 . (We do not use the *entire* preimage, which could indeed be infinite.)
. (We do not use the *entire* preimage, which could indeed be infinite.)
18 September, 2023 at 6:35 pm
Anonymous
thanks a lot
21 February, 2024 at 11:00 am
Sundara Narasimhan
Is the invariant mean not necessarily a continuous linear functional of ?
?
I’m trying to see an invariant mean on , one candidate should exist because
, one candidate should exist because  is amenable. If it was a continuous positive linear functional with total mass 1, it should be in of the form
is amenable. If it was a continuous positive linear functional with total mass 1, it should be in of the form  and such that
and such that  . It is also
. It is also 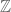 invariant, so it would force all
invariant, so it would force all  to be equal. However, such a choice of
to be equal. However, such a choice of  does not exist.
does not exist.
So what is a good candidate for the invariant mean? Am I missing some easy non-continous candidate?
24 February, 2024 at 1:13 pm
Terence Tao
One needs the axiom of choice (or some slightly weaker version thereof, such as the ultrafilter lemma) in order to construct an invariant mean. I discuss these means further at https://terrytao.wordpress.com/2017/05/11/generalisations-of-the-limit-functional/
Note that the Riesz representation theorem concerns continuous linear functionals on , rather than
, rather than  , so does not preclude the possibility of continuous linear functionals on
, so does not preclude the possibility of continuous linear functionals on  that don’t arise from finite measures on
that don’t arise from finite measures on  (and indeed the Hahn-Banach theorem provides such functionals).
(and indeed the Hahn-Banach theorem provides such functionals).
10 May, 2024 at 5:54 am
Anonymous
In the proof of Proposition4, is
supposed to be with E_1 rather than E_{-1}, and adding a union with {e} as well?
e_1cdot(Acap({e}cup E_1cup E_2cup E_{-2}))
As written now I don’t think it is contained in E_1 (if e_{-1}in A, for example), neither is it the set e_1cdot(Asetminus E_{-1}), which appears in its place in the next inequality.
[Corrected, thanks – T.]