In mathematics, one frequently starts with some space and wishes to extend it to a larger space
. Generally speaking, there are two ways in which one can extend a space
:
- By embedding
into a space
that has
(or at least an isomorphic copy of
) as a subspace.
- By covering
by a space
that has
(or an isomorphic copy thereof) as a quotient.
For many important categories of interest (such as abelian categories), the former type of extension can be represented by the exact sequence,
and the latter type of extension be represented by the exact sequence
In some cases, can be both embedded in, and covered by,
, in a consistent fashion; in such cases we sometimes say that the above exact sequences split.
An analogy would be to that of digital images. When a computer represents an image, it is limited both by the scope of the image (what it is picturing), and by the resolution of an image (how much physical space is represented by a given pixel). To make the image “larger”, one could either embed the image in an image of larger scope but equal resolution (e.g. embedding a picture of a pixel image of person’s face into a
pixel image that covers a region of space that is four times larger in both dimensions, e.g. the person’s upper body) or cover the image with an image of higher resolution but of equal scope (e.g. enhancing a
pixel picture of a face to a
pixel of the same face). In the former case, the original image is a sub-image (or cropped image) of the extension, but in the latter case the original image is a quotient (or a pixelation) of the extension. In the former case, each pixel in the original image can be identified with a pixel in the extension, but not every pixel in the extension is covered. In the latter case, every pixel in the original image is covered by several pixels in the extension, but the pixel in the original image is not canonically identified with any particular pixel in the extension that covers it; it “loses its identity” by dispersing into higher resolution pixels.
(Note that “zooming in” the visual representation of an image by making each pixel occupy a larger region of the screen neither increases the scope or the resolution; in this language, a zoomed-in version of an image is merely an isomorphic copy of the original image; it carries the same amount of information as the original image, but has been represented in a new coordinate system which may make it easier to view, especially to the visually impaired.)
In the study of a given category of spaces (e.g. topological spaces, manifolds, groups, fields, etc.), embedding and coverings are both important; this is particularly true in the more topological areas of mathematics, such as manifold theory. But typically, the term extension is reserved for just one of these two operations. For instance, in the category of fields, coverings are quite trivial; if one covers a field by a field
, the kernel of the covering map
is necessarily trivial and so
are in fact isomorphic. So in field theory, a field extension refers to an embedding of a field, rather than a covering of a field. Similarly, in the theory of metric spaces, there are no non-trivial isometric coverings of a metric space, and so the only useful notion of an extension of a metric space is the one given by embedding the original space in the extension.
On the other hand, in group theory (and in group-like theories, such as the theory of dynamical systems, which studies group actions), the term “extension” is reserved for coverings, rather than for embeddings. I think one of the main reasons for this is that coverings of groups automatically generate a special type of embedding (a normal embedding), whereas most embeddings don’t generate coverings. More precisely, given a group extension of a base group
,
one can form the kernel of the covering map
, which is a normal subgroup of
, and we thus can extend the above sequence canonically to a short exact sequence
On the other hand, an embedding of into
,
does not similarly extend to a short exact sequence unless the the embedding is normal.
Another reason for the notion of extension varying between embeddings and coverings from subject to subject is that there are various natural duality operations (and more generally, contravariant functors) which turn embeddings into coverings and vice versa. For instance, an embedding of one vector space into another
induces a covering of the dual space
by the dual space
, and conversely; similarly, an embedding of a locally compact abelian group
in another
induces a covering of the Pontryagin dual
by the Pontryagin dual
. In the language of images, embedding an image in an image of larger scope is largely equivalent to covering the Fourier transform of that image by a transform of higher resolution, and conversely; this is ultimately a manifestation of the basic fact that frequency is inversely proportional to wavelength.
Similarly, a common duality operation arises in many areas of mathematics by starting with a space and then considering a space
of functions on that space (e.g. continuous real-valued functions, if
was a topological space, or in more algebraic settings one could consider homomorphisms from
to some fixed space). Embedding
into
then induces a covering of
by
, and conversely, a covering of
by
induces an embedding of
into
. Returning again to the analogy with images, if one looks at the collection of all images of a fixed scope and resolution, rather than just a single image, then increasing the available resolution causes an embedding of the space of low-resolution images into the space of high-resolution images (since of course every low-resolution image is an example of a high-resolution image), whereas increasing the available scope causes a covering of the space of narrow-scope images by the space of wide-scope images (since every wide-scope image can be cropped into a narrow-scope image). Note in the case of images, that these extensions can be split: not only can a low-resolution image be viewed as a special case of a high-resolution image, but any high-resolution image can be pixelated into a low-resolution one. Similarly, not only can any wide-scope image be cropped into a narrow-scope one, a narrow-scope image can be extended to a wide-scope one simply by filling in all the new areas of scope with black (or by using more advanced image processing tools to create a more visually pleasing extension). (In the category of sets, the statement that every covering can be split is precisely the axiom of choice.)
I’ve recently found myself having to deal quite a bit with group extensions in my research, so I have decided to make some notes on the basic theory of such extensions here. This is utterly elementary material for a group theorist, but I found this task useful for organising my own thoughts on this topic, and also in pinning down some of the jargon in this field.
Definition 1 (Group extension) An extension of a group
is a group
, together with a surjective projection map (or covering map)
. If the kernel of
can be identified with (i.e. is isomorphic to) a group
, we say that
is an extension of
by
, and we have the short exact sequence
If the group
has some property
, we say that
is a
extension of
. Thus for instance, if
is abelian,
is an abelian extension of
; if
is central (in
),
is a central extension of
; and so forth. (Note that all extensions are automatically normal extensions, so we will almost never use the latter term.) We refer to
as the base of the extension, and
as the fibre, and refer to
and
collectively as factors of
.
If
has some property
, and
has some property
, then we say that
is
-by-
. (I have no idea why the order is traditionally arranged in this way; I would have thought that extending a
group by a
group would give a
-by-
group, rather than the other way around; perhaps at one point the idea of a normal embedding was considered more important than a group extension. Nevertheless, the notation seems to be entrenched by now.) Thus, for instance,
is abelian-by-finite if
is abelian and
is finite, but finite-by-abelian if
is finite and
is abelian.
One can think of a -by-
group as a group that looks like
“at large scales” and like
“at small scales”; one can also view this group as a principal
-bundle over
.
There are several ways to generate a group extension . Firstly, given any homomorphism
from one group
to another, the homomorphism theorem tells us that
is an extension of the image
, with kernel
:
Of course, every group extension arises in this manner.
A group extension splits if there is a homomorphism
such that
for all
. In this case,
acts on the kernel
by conjugation (after identifying
with
); denoting this action by
(thus
), we can then canonically identify
with the semi-direct product
, defined as the set of pairs
with
,
, with the group law
, by identifying
with
. Conversely, every semi-direct product
is a group extension of
by
which splits. If the conjugation action
is trivial, then the semi-direct product simplifies to the direct product
. In particular, any semi-direct product which is a central extension is of this form.
Note that, in general, an extension of by
is a different concept from an extension of
by
, because one can have
as a normal subgroup but not as a quotient, or vice versa. For instance,
has
as a normal subgroup, but not as a quotient;
is an extension of
by
, but not vice versa. To put it another way, the operator “-by-” is not commutative:
-by-
is a different concept from
-by-
.
A subgroup of an -by-
group is automatically an
-by-
group for some subgroups
of
respectively; this is essentially Goursat’s lemma. Furthermore, the index of the subgroup is the product of the index of
in
, and the index of
in
.
Some standard notions in group theory can be defined using group extensions.
- A metabelian group is the same thing as an abelian-by-abelian group, i.e. an abelian extension of an abelian group.
- A metacyclic group is the same thing as an cyclic-by-cyclic group, i.e. a cyclic extension of a cyclic group.
- A polycyclic group is defined recursively by declaring the trivial group to be polycyclic of length
, and defining a polycyclic group of length
to be an extension of a cyclic group by a polycyclic group of length
. Thus polycyclic groups are polycyclic-by-cyclic, where the polycyclic factor has a shorter length.
- A supersolvable group is defined recursively by declaring the trivial group to be supersolvable of length
, and defining a supersolvable group of length
to be a cyclic extension supersolvable group of length
. Thus supersolvable groups are cyclic-by-supersolvable, where the supersolvable factor has a shorter length. In other words, supersolvable groups are towers of cyclic extensions.
- A solvable group is defined recursively by declaring the trivial group to be solvable of length
, and defining a solvable group of length
to be an extension of an abelian group by a solvable group of length
. Thus solvable groups are solvable-by-abelian, where the solvable factor has a shorter length. One can equivalently define solvable groups as abelian-by-solvable, where the solvable factor again has a shorter length (because the final term in the derived series is abelian and normal). In other words, a solvable group is a tower of abelian extensions.
- A nilpotent group is defined recursively by declaring the trivial group to be nilpotent of step
, and defining a nilpotent group of step
to be a central extension of a nilpotent group of step
, thus nilpotent groups are central-by-nilpotent. In other words, a nilpotent group is a tower of central extensions.
(The inclusions here are: cyclic implies abelian implies metabelian implies solvable, cyclic implies metacyclic implies supersolvable implies polycyclic implies solvable, metacyclic implies metabelian, and abelian implies nilpotent implies solvable.)
The trivial group is the identity for the “-by-” operator: trivial-by- or
-by-trivial is the same thing as
.
Now we comment on the associativity of the “-by-” operator. If are groups, observe that an
-by-(
-by-
) group (i.e. an extension of an
-by-
group by
) is automatically an (
-by-
)-by-
group (i.e. an extension of
by an
-by-
group), since if we denote
by the
-by-(
-by-
) group, and
the quotient map from
to the
-by-
group, then
is a
-by-
normal subgroup of
whose quotient is
. Thus, for instance, every cyclic-by-metacyclic group is metacyclic-by-cyclic, and more generally every supersolvable group is polycyclic.
On the other hand, the converse is not true: not every (-by-
)-by-
group is an
-by-(
-by-
) group. The problem is that
is normal in the
-by-
group, but need not be normal in the (
-by-
)-by-
group. For instance, the semi-direct product
is (
-by-
)-by-
but not
-by-(
-by-
). So the “-by-” operation is not associative in general (for instance, there are polycyclic groups that are not supersolvable). However, if
is not just normal in the
-by-
group, but is characteristic in that group, then it is automatically normal in the larger (
-by-
)-by-
group, and then one can interpret the (
-by-
)-by-
group as an
-by-(
-by-
) group. So one recovers associativity when the first factor is characteristic. This explains why solvable groups can be recursively expressed both as abelian-by-solvable, and equivalently as solvable-by-abelian; this is ultimately because the commutator subgroup
is a characteristic subgroup of
. An easy but useful related observation is that solvable-by-solvable groups are again solvable (with the length of the product being bounded by the sum of the length of the factors).
Given a group property , a group
is said to be virtually
if it has a finite index subgroup with the property
; thus for instance a virtually abelian group is one with a finite index abelian subgroup, and so forth. (With this convention, “finite” is the same as “virtually trivial”.) This concept is not directly expressible in terms of group extensions for arbitrary properties
; however, if the group property
is hereditary in the sense that subgroups of a
group are also
, then a virtually
group is the same concept as a
-by-finite group. This is because every finite index subgroup
of a group
automatically contains a finite index normal subgroup of
. (Proof:
acts on the finite quotient space
by left multiplication, hence the stabiliser of
has finite index in
. But this stabliser is also normal in
and contained in
.)
One also observes that if ,
are hereditary properties, then the property of
-by-
is hereditary also; if
is a
-by-
group, and
is a subgroup of
, then the short exact sequence
where is a projection map, demonstrates that
is also a
-by-
group. Thus for instance the properties of being metabelian, metacyclic, polycyclic, supersolvable, solvable, or nilpotent, are hereditary. As a consequence, virtually nilpotent is the same as nilpotent-by-finite, etc.
We saw for hereditary properties that “
-by-finite” was the same concept as “virtually
“. It is natural to ask whether the same is true for “finite-by-
“. The answer is no; for instance, one can extend the an infinite vector space
over a finite field
by
(using some non-degenerate bilinear anti-symmetric form
, and defining
for
and
) to create a nilpotent group which is finite-by-abelian, but not virtually abelian. Conversely, the semi-direct product
(where
acts on
by reflection) is virtually abelian, but not finite-by-abelian. On the other hand, for hereditary
, a finite-by-
group is virtually (central finite)-by-
. This is because if
is an extension of a
group
by a finite group
, then
acts by conjugation on the finite group
; the stabiliser
of this action is then a finite index subgroup, whose intersection of
is then central in
. The projection of
onto
is also a
group by the hereditary nature of
, and the claim follows.
Remark 1 There is a variant of the above result which is also useful. Suppose one has an
-by-
group
in which the action of
on
is virtually trivial (i.e. there are only a finite number of distinct automorphisms of
induces by
. Then
is virtually a central
-by-
group for some finite index subgroups
of
.
One can phrase various results in group theory in a succinct form using this notation. For instance, one of the results in my earlier blog post on amenability now states that amenable-by-amenable groups are amenable. Another example that I have been looking at recently is this paper of Larsen and Pink, the main result of which is a classification of finite linear groups over a field of characteristic , namely that such groups are virtually (
-group by abelian) by (semisimple of Lie type), where one has bounds on the index of the “virtually” and on the type of the semisimple group.

21 comments
Comments feed for this article
23 January, 2010 at 2:38 am
Sam
Thanks for this review, but I’m slightly puzzled with the order of the factors in the -by- operator.
In definition 1, you say that if G is an extension of a group H with property Q by a group K with property P, it is a Q-by-P group. This sounds logical to me. But what is strange is that you seem to call G a K-by-H group (just below definition 1). Four paragraphs further, you speak about H-by-K groups. There is either a typo or a confusing change of convention. In the next paragraphs, you seem to be calling an extension of H by K a K-by-H group.
Finally in the paragraph about hereditary properties, G is an extension of Q by P, which you say is a (calligraphic) P-by-Q group. To be consistent with the definition 1, this means that P should have property Q and vice versae…
23 January, 2010 at 8:40 am
Terence Tao
Oops, I had the definition the wrong way around; an extension of H by K is (confusingly) a K-by-H group rather than an H-by-K group. I don’t know why these conventions are the way they are, but I guess it comes from reading the exact sequence 0 -> K -> G -> H -> 0 from left to right.
23 January, 2010 at 6:22 am
Prashant V
Dear Terry,
Are there any analogues of the Isomorphism Extension Theorem for groups? Can one always extend a group isomorphism?
23 January, 2010 at 8:46 am
Terence Tao
Well, group extensions are defined by covering rather than by embedding, so the question does not really make sense for group extensions (if G extends H, and H’ is isomorphic to H, then G automatically extends H’ also). But for embeddings (if H is embedded in G, and H is isomorphic to H’, then the isomorphism can be extended to one between G and G’ for some G’ containing H’), it seems to me that the same Zorn’s lemma argument would work here.
23 January, 2010 at 1:34 pm
John Armstrong
We can embed by
by 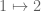 .
.
We can embed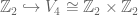 by including into one of the factors.
by including into one of the factors.
But clearly .
.
23 January, 2010 at 2:28 pm
Terence Tao
Well, yes, but in that case I don’t pick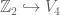 as my embedding of H’ in a larger group G’. I would pick
as my embedding of H’ in a larger group G’. I would pick  .
.
It does mean, though, that as currently phrased in my comment, the proposed group isomorphism extension theorem is a triviality; if H and H’ are isomorphic, and H can be embedded in G, then clearly H’ can be embedded in G also.
A slightly more interesting result is that if H is embedded in G, and H’ is isomorphic to H and embedded in G’, then one can simultaneously embed H, H’, G, G’ into a single object, the amalgamated free product of G and G’ over H, in such a way that H, H’ become identified. I guess the existence of the amalgamated free product is the closest analogue to the field isomorphism extension theorem in group theory.
23 January, 2010 at 2:49 pm
John Armstrong
Oh yes, if you’re free to choose the target then it’s trivial.
I was thinking Prashant was asking for something like a rigidity theorem, where under certain circumstances the behavior of the whole structure is essentially determined by a certain substructure. Then if two structures’ particular substructures are isomorphic, then the entire structures are isomorphic.
23 January, 2010 at 10:12 am
Anonymous
Perhaps this post deserves an expository tag.
[Fair enough – T.]
23 January, 2010 at 11:45 pm
Nate
in definition 1 paragraph 2, there is a typo (if i understand the conventions correctly): it reads “if K is central in G, K is a central extension of H” but i think it should read “if K is central in G, G is a central extension of H”
[Corrected, thanks – T.]
29 January, 2010 at 12:13 am
Anonymous
Just to clarify that there are at least two meanings of “embedding”. One is that of an injective morphism (as in the wikipedia article); another is when X is isomorphic to the image under the embedding. The two are not equivalent, although for the groups example, the two are indeed the same. For example, the identity map takes the normed sequence space l^1 into l^infty, so l^1 is “embedded” in l^infty in the first sense but not in the second. This example also illustrates that an embedding/extension (in the first sense) can also be thought of as a pixelation: the norm on l^1 is “finer” than the “hazier” one on l^infty.
30 May, 2011 at 4:39 pm
van Dantzig’s theorem « What’s new
[…] semidirect products as examples, but can be more general than these situations, as discussed in this previous blog post). In principle, the problem of understanding the structure of then splits into three simpler […]
8 October, 2011 at 12:57 pm
254A, Notes 5: The structure of locally compact groups, and Hilbert’s fifth problem « What’s new
[…] the combined group , due to the possible presence of non-trivial group cohomology. See for instance this previous blog post for more […]
27 April, 2013 at 9:25 pm
Notes on the classification of complex Lie algebras | What's new
[…] associative: every Lie algebra of the form is also of the form , but the converse is not true (see this previous blog post for some related discussion). As we are working in the infinitesimal world of Lie algebras (which […]
19 November, 2013 at 3:37 am
Srinivas Rau
Does the fundamental group of a compact Riemann surface have a universal central extension 0—>Z—->G—>pi(X)—>0 as claimed by Atiyah -Bott (1982)?
21 March, 2018 at 5:47 am
Mudheher Al-Bayati
How we can define a extending dynamical system depending on group extension concept ?
1 July, 2018 at 11:00 pm
Matthis
Dear Terence,
at the moment I am working on my bachelor thesis with the topic group extensions. Your overview is great and an interesting result is that a subgroup of an K-by-H extension is an K’-by-H’ extension with K’ and H’ subgroups of K and H. You say the proof is essentially Goursat’s Lemma but I just can’t figure out how this should work. Perhaps it’s just missing experience and know-how in group theory…
Maybe you can start me off?
Thanks a lot!
2 July, 2018 at 7:08 am
Terence Tao
What have you tried so far, and what did you get?
If you are more comfortable with linear algebra than with group theory, one can work with the analogous problem involving vector spaces over a fixed field (e.g. real vector spaces). If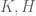 are vector spaces, a
are vector spaces, a  -by-
-by- vector space is a space
vector space is a space  which has a linear map onto
which has a linear map onto  with kernel
with kernel  . The assertion for groups has an exact analogue in this category (replacing “subgroup” by “subspace” of course), and you may find it easier to prove from your linear algebra intuition.
. The assertion for groups has an exact analogue in this category (replacing “subgroup” by “subspace” of course), and you may find it easier to prove from your linear algebra intuition.
Another category where the analogous result is true is that of sets, although here the claim is somewhat degenerate and perhaps too easy to prove. If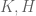 are disjoint sets, a
are disjoint sets, a  -by-
-by- set would be a set
set would be a set  that contains a subset
that contains a subset  such that the set-theoretic difference
such that the set-theoretic difference  is equal to
is equal to  . (This notion is rather degenerate since there is precisely one such extension, namely
. (This notion is rather degenerate since there is precisely one such extension, namely  .) The corresponding claim is then rather trivial, but it may still give you a bit of intuition, in particular with regards to how
.) The corresponding claim is then rather trivial, but it may still give you a bit of intuition, in particular with regards to how 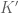 and
and 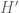 are actually related to
are actually related to 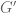 ,
,  , and
, and  .
.
3 July, 2018 at 12:10 am
Matthis
Thank you for your response!
I was desperate trying to someway connect the group extension problem with Goursat’s lemma without assuming my extension was a direct product, I did not came that far.
Thinking about the analogous problem with vector spaces helped!
For a K-by-H extension G I get a homomorphism f from G with Im(f)=H and Ker(f)=K. So for a subgroup G’ from G I call the intersection of K and G’ K’ and this is the kernel of f restricted to G’. For H’ I take the image of G’ under f.
I wrote it down and thought it through and it seems to work, assuming I did not make an embarrassing mistake.
But is it that simple? What does that have to do with Goursat’s lemma?
4 July, 2018 at 8:19 am
Terence Tao
This result does not directly invoke Goursat’s lemma (which derives a stronger conclusion assuming stronger hypotheses) but the two results are in the same spirit and use similar tools in the proof.
27 March, 2019 at 2:35 pm
Kit
Dear Terence,
I am in my final year of my bachelors and I am doing my dissertation on subgroup lattices. While working through some proofs I have become stuck on results that use group extensions. In particular the book I am using often justifies a subgroup being abelian because it is “a cyclic extension of a central subgroup”.
I don’t really understand what this means (this post has been a big help!) or why it would lead to the subgroup being abelian.
Any help would be greatly appreciated, thank you for your time!
27 March, 2019 at 3:41 pm
Terence Tao
If a group is formed by an extension of a central subgroup
is formed by an extension of a central subgroup  by a cyclic group
by a cyclic group  generated by some generator
generated by some generator  (so the short exact sequence
(so the short exact sequence  splits, with
splits, with  now being a subgroup of
now being a subgroup of  as well as a quotient), then
as well as a quotient), then  and
and  both commute with
both commute with  (as
(as  is central), and
is central), and  of course commutes with itself. Since
of course commutes with itself. Since  and
and  together generate the group
together generate the group  , the entire group
, the entire group  is then abelian.
is then abelian.