A fundamental characteristic of many mathematical spaces (e.g. vector spaces, metric spaces, topological spaces, etc.) is their dimension, which measures the “complexity” or “degrees of freedom” inherent in the space. There is no single notion of dimension; instead, there are a variety of different versions of this concept, with different versions being suitable for different classes of mathematical spaces. Typically, a single mathematical object may have several subtly different notions of dimension that one can place on it, which will be related to each other, and which will often agree with each other in “non-pathological” cases, but can also deviate from each other in many other situations. For instance:
- One can define the dimension of a space
by seeing how it compares to some standard reference spaces, such as
or
; one may view a space as having dimension
if it can be (locally or globally) identified with a standard
-dimensional space. The dimension of a vector space or a manifold can be defined in this fashion.
- Another way to define dimension of a space
is as the largest number of “independent” objects one can place inside that space; this can be used to give an alternate notion of dimension for a vector space, or of an algebraic variety, as well as the closely related notion of the transcendence degree of a field. The concept of VC dimension in machine learning also broadly falls into this category.
- One can also try to define dimension inductively, for instance declaring a space
to be
-dimensional if it can be “separated” somehow by an
-dimensional object; thus an
-dimensional object will tend to have “maximal chains” of sub-objects of length
(or
, depending on how one initialises the chain and how one defines length). This can give a notion of dimension for a topological space or a commutative ring.
The notions of dimension as defined above tend to necessarily take values in the natural numbers (or the cardinal numbers); there is no such space as , for instance, nor can one talk about a basis consisting of
linearly independent elements, or a chain of maximal ideals of length
. There is however a somewhat different approach to the concept of dimension which makes no distinction between integer and non-integer dimensions, and is suitable for studying “rough” sets such as fractals. The starting point is to observe that in the
-dimensional space
, the volume
of a ball of radius
grows like
, thus giving the following heuristic relationship
between volume, scale, and dimension. Formalising this heuristic leads to a number of useful notions of dimension for subsets of (or more generally, for metric spaces), including (upper and lower) Minkowski dimension (also known as box-packing dimension or Minkowski-Bougliand dimension), and Hausdorff dimension.
[In -theory, it is also convenient to work with “virtual” vector spaces or vector bundles, such as formal differences of such spaces, and which may therefore have a negative dimension; but as far as I am aware there is no connection between this notion of dimension and the metric ones given here.]
Minkowski dimension can either be defined externally (relating the external volume of -neighbourhoods of a set
to the scale
) or internally (relating the internal
-entropy of
to the scale). Hausdorff dimension is defined internally by first introducing the
-dimensional Hausdorff measure of a set
for any parameter
, which generalises the familiar notions of length, area, and volume to non-integer dimensions, or to rough sets, and is of interest in its own right. Hausdorff dimension has a lengthier definition than its Minkowski counterpart, but is more robust with respect to operations such as countable unions, and is generally accepted as the “standard” notion of dimension in metric spaces. We will compare these concepts against each other later in these notes.
One use of the notion of dimension is to create finer distinctions between various types of “small” subsets of spaces such as , beyond what can be achieved by the usual Lebesgue measure (or Baire category). For instance, a point, line, and plane in
all have zero measure with respect to three-dimensional Lebesgue measure (and are nowhere dense), but of course have different dimensions (
,
, and
respectively). (The Kakeya set conjecture, discussed recently on this blog, offers another good example.) This can be used to clarify the nature of various singularities, such as that arising from non-smooth solutions to PDE; a function which is non-smooth on a set of large Hausdorff dimension can be considered less smooth than one which is non-smooth on a set of small Hausdorff dimension, even if both are smooth almost everywhere. While many properties of the singular set of such a function are worth studying (e.g. their rectifiability), understanding their dimension is often an important starting point. The interplay between these types of concepts is the subject of geometric measure theory.
— 1. Minkowski dimension —
Before we study the more standard notion of Hausdorff dimension, we begin with the more elementary concept of the (upper and lower) Minkowski dimension of a subset of a Euclidean space
.
There are several equivalent ways to approach Minkowski dimension. We begin with an “external” approach, based on a study of the -neighbourhoods
of
, where
and we use the Euclidean metric on
. These are open sets in
and therefore have a
-dimensional volume (or Lebesgue measure)
. To avoid divergences, let us assume for now that
is bounded, so that the
have finite volume.
Let . Suppose
is a bounded portion of a
-dimensional subspace, e.g.
, where
is the unit ball in
and we identify
with
in the usual manner. Then we see from the triangle inequality that
for all , which implies that
for some constants depending only on
. In particular, we have
(compare with (1)). This motivates our first definition of Minkowski dimension:
Definition 1 Let
be a bounded subset of
. The upper Minkowski dimension
is defined as
and the lower Minkowski dimension
is defined as
If the upper and lower Minkowski dimensions match, we refer to
as the Minkowski dimension of
. In particular, the empty set has a Minkowski dimension of
.
Unwrapping all the definitions, we have the following equivalent formulation, where is a bounded subset of
and
:
- We have
iff for every
, one has
for all sufficiently small
and some
.
- We have
iff for every
, one has
for arbitrarily small
and some
.
- We have
iff for every
, one has
for arbitrarily small
and some
.
- We have
iff for every
, one has
for all sufficiently small
and some
.
- (i) Let
be the Cantor set consisting of all base
strings
, where each
takes values in
. Show that
has Minkowski dimension
. (Hint: approximate any small
by a negative power of
.)
- (ii) Let
be the Cantor set consisting of all base
strings
, where each
takes values in
when
for some integer
, and
is arbitrary for the other values of
. Show that
has a lower Minkowski dimension of
and an upper Minkowski dimension of
.
Exercise 3 Suppose that
is a compact set with the property that there exist
and an integer
such that
is equal to the union of
disjoint translates of
. (This is a special case of a self-similar fractal; the Cantor set is a typical example.) Show that
has Minkowski dimension
.
If thetranslates of
are allowed to overlap, establish the upper bound
.
It is clear that we have the inequalities
for non-empty bounded , and the monotonicity properties
whenever are bounded sets. It is thus natural to extend the definitions of lower and upper Minkowski dimension to unbounded sets
by defining
In particular, we easily verify that -dimensional subspaces of
have Minkowski dimension
.
Exercise 4 Show that any subset of
with lower Minkowski dimension less than
has Lebesgue measure zero. In particular, any subset
of positive Lebesgue measure must have full Minkowski dimension
.
Now we turn to other formulations of Minkowski dimension. Given a bounded set and
, we make the following definitions:
(the external
-covering number of
) is the fewest number of open balls of radius
with centres in
needed to cover
.
(the internal
-covering number of
) is the fewest number of open balls of radius
with centres in
needed to cover
.
(the
-metric entropy) is the cardinality of the largest
-net in
, i.e. the largest set
in
such that
for every
.
(the
-packing number of
) is the largest number of disjoint open balls one can find of radius
with centres in
.
These three quantities are closely related to each other, and to the volumes :
Exercise 5 For any bounded set
and any
, show that
and
As a consequence of this exercise, we see that
where is any of
.
One can now take the formulae (4), (5) as the definition of Minkowski dimension for bounded sets (and then use (2), (3) to extend to unbounded sets). The formulations (4), (5) for have the advantage of being intrinsic – they only involve
, rather than the ambient space
. For metric spaces, one still has a partial analogue of Exercise 5, namely
As such, these formulations of Minkowski dimension extend without any difficulty to arbitrary bounded metric spaces (at least when the spaces are locally compact), and then to unbounded metric spaces by (2), (3).
Exercise 6 If
is a Lipschitz map between metric spaces, show that
and
for all
. Conclude in particular that the graph
of any Lipschitz function
has Minkowski dimension
, and the graph of any measurable function
has Minkowski dimension at least
.
Note however that the dimension of graphs can become larger than that of the base in the non-Lipschitz case:
Exercise 8 Let
be a bounded metric space. For each
, let
be a maximal
-net of
(thus the cardinality of
is
). Show that for any continuous function
, one has the inequality
(Hint: For any
, define
to be the nearest point in
to
, and use a telescoping series.) This inequality (and variants thereof), which replaces a continuous supremum of a function
by a sum of discrete suprema of differences
of that function, is the basis of the generic chaining technique in probability, used to estimate the supremum of a continuous family of random processes. It is particularly effective when combined with bounds on the metric entropy
, which of course is closely related to the Minkowski dimension of
, and with large deviation bounds on the differences
. A good reference for generic chaining is the text by Talagrand.
Exercise 9 If
and
are bounded sets, show that
and
Give a counterexample that shows that either of the inequalities here can be strict. (Hint: There are many possible constructions; one of them is a modification of Exercise 2(ii).)
It is easy to see that Minkowski dimension reacts well to finite unions, and more precisely that
and
for any . However, it does not respect countable unions. For instance, the rationals
have Minkowski dimension
, despite being the countable union of points, which of course have Minkowski dimension
. More generally, it is not difficult to see that any set
has the same upper or lower Minkowski dimension as its topological closure
, since both sets have the same
-neighbourhoods. Thus we see that the notion of Minkowski dimension misses some of the fine structure of a set
, in particular the presence of “holes” within the set. We now turn to the notion of Hausdorff dimension, which rectifies some of these defects.
— 2. Hausdorff measure —
The Hausdorff approach to dimension begins by noting that -dimensional objects in
tend to have a meaningful
-dimensional measure to assign to them. For instance, the
-dimensional boundary of a polygon has a perimeter, the
-dimensional vertices of that polygon have a cardinality, and the polygon itself has an area. So to define the notion of a
-Hausdorff dimensional set, we will first define the notion of the
-dimensional Hausdorff measure
of a set
.
To do this, let us quickly review one of the (many) constructions of -dimensional Lebesgue measure, which we are denoting here by
. One way to build this measure is to work with half-open boxes
in
, which we assign a volume of
. Given this notion of volume for boxes, we can then define the outer Lebesgue measure
of any set
by the formula
where the infimum ranges over all at most countable collections of boxes that cover
. One easily verifies that
is indeed an outer measure (i.e. it is monotone, countably subadditive, and assigns zero to the empty set). We then define a set
to be
-measurable if one has the additivity property
for all . By Carathéodory’s theorem, the space of
-measurable sets is a
-algebra, and outer Lebesgue measure is a countably additive measure on this
-algebra, which we denote
. Furthermore, one easily verifies that every box
is
-measurable, which soon implies that every Borel set is also; thus Lebesgue measure is a Borel measure (though it can of course measure some non-Borel sets also).
Finally, one needs to verify that the Lebesgue measure of a box is equal to its classical volume
; the above construction trivially gives
but the converse is not as obvious. This is in fact a rather delicate matter, relying in particular on the completeness of the reals; if one replaced
by the rationals
, for instance, then all the above constructions go through but now boxes have Lebesgue measure zero (why?). See Chapter 1 of Folland’s book, for instance, for details.
Anyway, we can use this construction of Lebesgue measure as a model for building -dimensional Hausdorff measure. Instead of using half-open boxes as the building blocks, we will instead work with the open balls
. For
-dimensional measure, we will assign each ball
a measure
(cf. (1)). We can then define the unlimited Hausdorff content
of a set
by the formula
where the infimum ranges over all at most countable families of balls that cover . (Note that if
is compact, then it would suffice to use finite coverings, since every open cover of
has a finite subcover. But in general, for non-compact
we must allow the use of infinitely many balls.)
As with Lebesgue measure, is easily seen to be an outer measure, and one could define the notion of a
-measurable set on which Carathéodory’s theorem applies to build a countably additive measre. Unfortunately, a key problem arises: once
is less than
, most sets cease to be
-measurable! We illustrate this in the one-dimensional case with
and
, and consider the problem of computing the unlimited Hausdorff content
. On the one hand, this content is at most
, since one can cover
by the ball of radius
centred at
for any
. On the other hand, the content is also at least
. To see this, suppose we cover
by a finite or countable family of balls
(one can reduce to the finite case by compactness, though it isn’t necessary to do so here). The total one-dimensional Lebesgue measure
of these balls must equal or exceed the Lebesgue measure of the entire interval
, thus
From the inequality (which is obvious after expanding the RHS and discarding cross-terms) we see that
and the claim follows.
We now see some serious breakdown of additivity: for instance, the unlimited -dimensional content of
is
, despite being the disjoint union of
and
, which each have an unlimited content of
. In particular, this shows that
(for instance) is not measurable with respect to the unlimited content. The basic problem here is that the most efficient cover of a union such as
for the purposes of unlimited
-dimensional content is not coming from covers of the separate components
and
of that union, but is instead coming from one giant ball that covers
directly.
To fix this, we will limit the Hausdorff content by working only with small balls. More precisely, for any , we define the Hausdorff content
of a set
by the formula
where the balls are now restricted to be less than or equal to
in radius. This quantity is decreasing in
, and we then define the Hausdorff outer measure
by the formula
(This is analogous to the Riemann integral approach to volume of sets, covering them by balls, boxes, or rectangles of increasingly small size; this latter approach is also closely connected to the Minkowski dimension concept studied earlier. The key difference between the Lebesgue/Hausdorff approach and the Riemann/Minkowski approach is that in the former approach one allows the balls or boxes to be countable in number, and to be variable in size, whereas in the latter approach the cover is finite and uniform in size.)
Exercise 10 Show that if
, then
for all
. Thus
-dimensional Hausdorff measure is only a non-trivial concept for subsets of
in the regime
.
Since each of the are outer measures,
is also. But the key advantage of moving to the Hausdorff measure rather than Hausdorff content is that we obtain a lot more additivity. For instance:
Exercise 11 Let
be subsets of
which have a non-zero separation, i.e. the quantity
is strictly positive. Show that
. (Hint: one inequality is easy. For the other, observe that any small ball can intersect
or intersect
, but not both.)
One consequence of this is that there is a large class of measurable sets:
Proposition 12 Let
. Then every Borel subset of
is
-measurable.
Proof: Since the collection of -measurable sets is a
-algebra, it suffices to show the claim for closed sets
. (It will be slightly more convenient technically to work with closed sets rather than open ones here.) Thus, we take an arbitrary set
and seek to show that
We may assume that and
are both finite, since the claim is obvious otherwise from monotonicity.
From Exercise 11 and the fact that is an outer measure, we already have
where is the
-neighbourhood of
. So it suffices to show that
For any , we have the telescoping sum
, where
, and thus by countable subadditivity and monotonicity
so it suffices to show that the sum is absolutely convergent.
Consider the even-indexed sets . These sets are separated from each other, so by many applications of Exercise 11 followed by monotonicity we have
for all , and thus
is absolutely convergent. Similarly for
, and the claim follows.
On the -measurable sets
, we write
for
, thus
is a Borel measure on
. We now study what this measure looks like for various values of
. The case
is easy:
Exercise 13 Show that every subset of
is
-measurable, and that
is counting measure.
Now we look at the opposite case . It is easy to see that any Lebesgue-null set of
has
-dimensional Hausdorff measure zero (since it may be covered by balls of arbitrarily small total content). Thus
-dimensional Hausdorff measure is absolutely continuous with respect to Lebesgue measure, and we thus have
for some locally integrable function
. As Hausdorff measure and Lebesgue measure are clearly translation-invariant,
must also be translation-invariant and thus constant. We therefore have
for some constant .
We now compute what this constant is. If denotes the volume of the unit ball
, then we have
for any at most countable collection of balls . Taking infima, we conclude that
and so .
In the opposite direction, observe from Exercise 5 that given any , one can cover the unit cube
by at most
balls of radius
, where
depends only on
; thus
and so ; in particular,
is finite.
We can in fact compute explicitly (although knowing that
is finite and non-zero already suffices for many applications):
Lemma 14 We have
, or in other words
. (In particular, a ball
has
-dimensional Hausdorff measure
.)
Proof: Let us consider the Hausdorff measure of the unit cube. By definition, for any
one can find an
such that
Observe (using Exercise 5) that we can find at least disjoint balls
of radius
inside the unit cube. We then observe that
On the other hand,
putting all this together, we obtain
which rearranges as
Since is bounded below by
, we can then send
and conclude that
; since we already showed
, the claim follows.
Thus -dimensional Hausdorff measure is an explicit constant multiple of
-dimensional Lebesgue measure. The same argument shows that for integers
, the restriction of
-dimensional Hausdorff measure to any
-dimensional linear subspace (or affine subspace)
is equal to the constant
times
-dimensional Lebesgue measure on
. (This shows, by the way, that
is not a
-finite measure on
in general, since one can partition
into uncountably many
-dimensional affine subspaces. In particular, it is not a Radon measure in general).
One can then compute -dimensional Hausdorff measure for other sets than subsets of
-dimensional affine subspaces by changes of variable. For instance:
Exercise 15 Let
be an integer, let
be an open subset of
, and let
be a smooth injective map which is non-degenerate in the sense that the Hessian
(which is a
matrix) has full rank at every point of
. For any compact subset
of
, establish the formula
where the Jacobian
is the square root of the sum of squares of all the determinants of the
minors of the
matrix
. (Hint: By working locally, one can assume that
is the graph of some map from
to
, and so can be inverted by the projection function; by working even more locally, one can assume that the Jacobian is within an epsilon of being constant. The image of a small ball in
then resembles a small ellipsoid in
, and conversely the projection of a small ball in
is a small ellipsoid in
. Use some linear algebra and several variable calculus to relate the content of these ellipsoids to the radius of the ball.) It is possible to extend this formula to Lipschitz maps
that are not necessarily injective, leading to the area formula
for such maps, but we will not prove this formula here.
From this exercise we see that -dimensional Hausdorff measure does coincide to a large extent with the
-dimensional notion of surface area; for instance, for a simple smooth curve
with everywhere non-vanishing derivative, the
measure of
is equal to its classical length
. One can also handle a certain amount of singularity (e.g. piecewise smooth non-degenerate curves rather than everywhere smooth non-degenerate curves) by exploiting the countable additivity of
measure, or by using the area formula alluded to earlier.
Now we see how the Hausdorff dimension varies in .
Exercise 16 Let
, and let
be a Borel set. Show that if
is finite, then
is zero; equivalently, if
is positive, then
is infinite.
Example 17 Let
be integers. The unit ball
has a
-dimensional Hausdorff measure of
(by Lemma 14), and so it has zero
-dimensional Hausdorff dimensional measure for
and infinite
-dimensional measure for
.
On the other hand, we know from Exercise 13 that is positive for any non-empty set
, and that
for every
. We conclude (from the least upper bound property of the reals) that for any Borel set
, there exists a unique number in
, called the Hausdorff dimension
of
, such that
for all
and
for all
. Note that at the critical dimension
itself, we allow
to be zero, finite, or infinite, and we shall shortly see in fact that all three possibilities can occur. By convention, we give the empty set a Hausdorff dimension of
. One can also assign Hausdorff dimension to non-Borel sets, but we shall not do so to avoid some (very minor) technicalities.
Example 18 The unit ball
has Hausdorff dimension
, as does
itself. Note that the former set has finite
-dimensional Hausdorff measure, while the latter has an infinite measure. More generally, any
-dimensional smooth manifold in
has Hausdorff dimension
.
Exercise 19 Show that the graph
has Hausdorff dimension
; compare this with Exercise 7.
It is clear that Hausdorff dimension is monotone: if are Borel sets, then
. Since Hausdorff measure is countably additive, it is also not hard to see that Hausdorff dimension interacts well with countable unions:
Thus for instance the rationals, being a countable union of -dimensional points, have Hausdorff dimension
, in contrast to their Minkowski dimension of
. On the other hand, we at least have an inequality between Hausdorff and Minkowski dimension:
Exercise 20 For any Borel set
, show that
. (Hint: use (5). Which of the choices of
is most convenient to use here?)
It is instructive to compare Hausdorff dimension and Minkowski dimension as follows.
Exercise 21 Let
be a bounded Borel subset of
, and let
.
- Show that
if and only if, for every
and arbitrarily small
, one can cover
by finitely many balls
of radii
equal to
such that
.
- Show that
if and only if, for every
and all sufficiently small
, one can cover
by finitely many balls
of radii
equal to
such that
.
- Show that
if and only if, for every
and
, one can cover
by countably many balls
of radii
at most
such that
.
The previous two exercises give ways to upper-bound the Hausdorff dimension; for instance, we see from Exercise 3 that self-similar fractals of the type in that exercise (i.e.
is
translates of
) have Hausdorff dimension at most
. To lower bound the Hausdorff dimension of a set
, one convenient way to do so is to find a measure with a certain “dimension” property (analogous to (1)) that assigns a positive mass to
:
Exercise 22 Let
. A Borel measure
on
is said to be a Frostman measure of dimension at least
if it is compactly supported there exists a constant
such that
for all balls
of radius
. Show that if
has dimension at least
, then any Borel set
with
has positive
-dimensional Hausdorff content; in particular,
.
Note that this gives an alternate way to justify the fact that smooth -dimensional manifolds have Hausdorff dimension
, since on the one hand they have Minkowski dimension
, and on the other hand they support a non-trivial
-dimensional measure, namely Lebesgue measure.
Exercise 23 Show that the Cantor set in Exercise 2(i) has Hausdorff dimension
. More generally, establish the analogue of the first part of Exercise 3 for Hausdorff measure.
Exercise 24 Construct a subset of
of Hausdorff dimension
that has zero Lebesgue measure. (Hint: A modified Cantor set, vaguely reminiscent of Exercise 2(ii), can work here.)
A useful fact is that Exercise 22 can be reversed:
Lemma 25 (Frostman’s lemma) Let
, and let
be a compact set with
. Then there exists a non-trivial Frostman measure of dimension at least
supported on
(thus
and
).
Proof: Without loss of generality we may place the compact set in the half-open unit cube
. It is convenient to work dyadically. For each integer
, we subdivide
into
half-open cubes
of sidelength
in the usual manner, and refer to such cubes as dyadic cubes. For each
and any
, we can define the dyadic Hausdorff content
to be the quantity
where the range over all at most countable families of dyadic cubes of sidelength at most
that cover
. By covering cubes by balls and vice versa, it is not hard to see that
for some absolute constants depending only on
. Thus, if we define the dyadic Hausdorff measure
then we see that the dyadic and non-dyadic Huausdorff measures are comparable:
In particular, the quantity is strictly positive.
Given any dyadic cube of length
, define the upper Frostman content
to be the quantity
Then . By covering
by
, we also have the bound
Finally, by the subadditivity property of Hausdorff content, if we decompose into
cubes
of sidelength
, we have
The quantity behaves like a measure, but is subadditive rather than additive. Nevertheless, one can easily find another quantity
to assign to each dyadic cube such that
and
for all dyadic cubes, and such that
whenever a dyadic cube is decomposed into sub-cubes of half the sidelength. Indeed, such a
can be constructed by a greedy algorithms starting at the largest cube
and working downward; we omit the details. One can then use this “measure”
to integrate any continuous compactly supported function on
(by approximating such a function by one which is constant on dyadic cubes of a certain scale), and so by the Riesz representation theorem, it extends to a Radon measure
supported on
. (One could also have used the Caratheódory extension theorem at this point.) Since
,
is non-trivial; since
for all dyadic cubes
, it is not hard to see that
is a Frostman measure of dimension at least
, as desired.
The study of Hausdorff dimension is then intimately tied to the study of the dimensional properties of various measures. We give some examples in the next few exercises.
Exercise 26 Let
, and let
be a compact set. Show that
if and only if, for every
, there exists a probability Borel measure
supported on
with
Show that this condition is also equivalent to
lying in the Sobolev space
. Thus we see a link here between Hausdorff dimension and Sobolev norms: the lower the dimension of a set, the rougher the measures that it can support, where the Sobolev scale is used to measure roughness.
Exercise 27 Let
be a compact subset of
, and let
be a Borel probability measure supported on
. Let
.
- Suppose that for every
, every
, and every subset
of
with
, one could establish the bound
for
equal to any of
(the exact choice of
is irrelevant thanks to Exercise 5). Show that
has Hausdorff dimension at least
. (Hint: cover
by small balls, then round the radius of each ball to the nearest power of
. Now use countable additivity and the observation that sum
is small when
ranges over sufficiently small powers of
.)
- Show that one can replace
with
in the previous statement. (Hint: instead of rounding the radius to the nearest power of
, round instead to radii of the form
for integers
.) This trick of using a hyper-dyadic range of scales rather than a dyadic range of scales is due to Bourgain. The exponent
in the double logarithm can be replaced by any other exponent strictly greater than
.
This should be compared with the task of lower bounding the lower Minkowski dimension, which only requires control on the entropy of
itself, rather than of large subsets
of
. The results of this exercise are exploited to establish lower bounds on the Hausdorff dimension of Kakeya sets (and in particular, to conclude such bounds from the Kakeya maximal function conjecture, as discussed in this previous post).
Exercise 28 Let
be a Borel set, and let
be a locally Lipschitz map. Show that
, and that if
has zero
-dimensional Hausdorff measure then so does
.
Exercise 29 Let
be a smooth function, and let
be a test function such that
on the support of
. Establish the co-area formula
(Hint: Subdivide the support of
to be small, and then apply a change of variables to make
linear, e.g.
.) This formula is in fact valid for all absolutely integrable
and Lipschitz
, but is difficult to prove for this level of generality, requiring a version of Sard’s theorem.
The coarea formula (6) can be used to link geometric inequalities to analytic ones. For instance, the sharp isoperimetric inequality
valid for bounded open sets in
, can be combined with the coarea formula (with
) to give the sharp Sobolev inequality
for any test function , the main point being that
is the boundary of
(one also needs to do some manipulations relating the volume of those level sets to
). We omit the details.
Further discussion of Hausdorff dimension can be found in the books of Falconer, of Mattila and of Wolff, as well as in many other places.

61 comments
Comments feed for this article
20 May, 2009 at 3:52 am
Frank Morgan
On infinite dimensional spaces, such as function spaces, there are many notions of small sets, such as category and measure 0, but the strongest is probably that of “positive codimension”; see B. White’s “Generic regularity of unoriented two-dimensional area minimizing surfaces,” MR MR794375.
20 May, 2009 at 3:59 am
Allen Knutson
[In {K}-theory, it is also convenient to work with “virtual” vector spaces or vector bundles, such as formal differences of such spaces, and which may therefore have a negative dimension; but as far as I am aware there is no connection between this notion of dimension and the metric ones given here.]
Interesting question. One way that those formal differences show up as honest dimensions is the following. If M is a topological space carrying a vector bundle V, and sigma is a generic section of V, then the dimension of sigma^{-1}(0) is dim M – dim V (where the second is the fiber dimension).
But for many purposes one may not want to take an actual section, e.g. because one doesn’t want to prejudice one over the other, or one may not have generic enough sections available because one’s working in a holomorphic context, or just because dim M – dim V would be negative (and so sigma^{-1}(0) would be empty). In such cases, rather than taking sigma^{-1}(0) as the object of interest, one should just keep around M and V, and declare the fibers to be odd vector bundles (in the supermanifold sense).
This point of view shows up (without mention of supermanifolds) in Fulton-MacPherson intersection theory, where the naive intersection M of two subvarieties is too big, and the correct intersection is represented by a vector bundle V over M, which may or may not have generic enough sections.
I don’t see any reason M can’t be a fractal. For these oddness purposes, I’m pretty sure V should be an actual vector bundle, not a bundle with fractal fibers.
Maybe you’d like this question. Let M,N be fractals, with dim M > dim N. Do “most” maps sigma from M -> N have the property that “most” fibers are fractals with dim = dim M – dim N? Add on whatever assumptions, e.g. compactness, you like.
20 May, 2009 at 8:37 am
Terence Tao
Maybe you’d like this question. Let M,N be fractals, with dim M > dim N. Do “most” maps sigma from M -> N have the property that “most” fibers are fractals with dim = dim M – dim N? Add on whatever assumptions, e.g. compactness, you like.
There are indeed results of this general flavour, though one often does have to assume various non-pathological assumptions, e.g. that various notions of dimension for M or N coincide. Here is a typical result (due to Marstrand, and later refined by Peres and Schlag, and stated somewhat informally): if is compact and has dimension d for some
is compact and has dimension d for some  , then the image of E under "most" orthogonal projections
, then the image of E under "most" orthogonal projections  has full dimension (and even positive measure). In fact the set of directions for which this statement fails has dimension at most
has full dimension (and even positive measure). In fact the set of directions for which this statement fails has dimension at most  . This isn't quite the type of thing you asked, but is in a similar spirit.
. This isn't quite the type of thing you asked, but is in a similar spirit.
Incidentally, if one defines the complex Hausdorff dimension of a set to be half the real dimension, then there are some "algebraic" examples of fractals in complex geometry: the real m-dimensional manifolds become m/2-dimensional in this sense. In particular the real line is now a 1/2-dimensional complex fractal. I suppose one could try building a half-integer K-theory of real sections of complex vector bundles (maybe restricting to real algebraic varieties to avoid some pathologies); it would probably be a good model for any putative "fractal K-theory".
21 May, 2009 at 12:08 am
gowers
Wow, I’d never thought about this general idea of trying to unify fractal dimension and topological ideas in this sort of way, but once one starts thinking along these lines then there seem to be lots of possibilities. For instance, could one develop a notion of cohomology in which one could prove statements like that if and
and  are suitable subsets of a
are suitable subsets of a  -dimensional set, then as you deform them in some suitable way the cohomology class of
-dimensional set, then as you deform them in some suitable way the cohomology class of 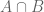 in the group
in the group  , where
, where  , does not change? And could one develop an infinitesimal boundary map (that is, one that reduces the dimension infinitesimally)? And in K-theory, could one have a continuous Bott periodicity theorem? Etc. etc. Do people think about this kind of question? And if so, is it generalization for the fun of it or is it conceivable that fractal algebraic topology could have applications?
, does not change? And could one develop an infinitesimal boundary map (that is, one that reduces the dimension infinitesimally)? And in K-theory, could one have a continuous Bott periodicity theorem? Etc. etc. Do people think about this kind of question? And if so, is it generalization for the fun of it or is it conceivable that fractal algebraic topology could have applications?
21 May, 2009 at 12:20 am
Vicky
On a rather less profound note, I think that n and d in the sentence including equation (1) should perhaps be the same. [Corrected, thanks – T.]
21 May, 2009 at 3:27 am
Frank Morgan
A simple remark on Terry’s question: in general the Hausdorff dimension of a product is greater than the sum of the Hausdorff dimensions of the factors (see http://en.wikipedia.org/wiki/Hausdorff_dimension).
21 May, 2009 at 9:09 am
Terence Tao
Dear Frank: Yes, to get a good theory (at least initially), one would have to exclude “pathological” sets (perhaps in analogy to how algebraic geometry works better when one only considers smooth varieties and transverse intersections; one can “fix” all these problems by passing to schemes, but I wouldn’t want to try to conjecture what a fractal scheme would look like yet). For instance, if one restricts attention to sets whose Hausdorff and Minkowski dimenion match, then one does recover the expected identity . Note that many standard examples of fractals, particularly self-similar fractals, do indeed have matching Hausdorff and Minkowski dimension. (It is also likely to help if one also assumes that the Hausdorff dimension matches some other useful notions of dimension as well, e.g. Fourier dimension.)
. Note that many standard examples of fractals, particularly self-similar fractals, do indeed have matching Hausdorff and Minkowski dimension. (It is also likely to help if one also assumes that the Hausdorff dimension matches some other useful notions of dimension as well, e.g. Fourier dimension.)
As I said before, perhaps an initial toy case would be that of trying to work out the cohomology or K-theory of smooth real manifolds or algebraic varieties inside complex manifolds (or complex vector bundles), as such “half-integer-dimensional complex fractals” are highly non-pathological in the analytic sense, even if they totally fail to have any complex structure. [Imagine for instance an alien race living in some complexified spacetime whose mathematicians had somehow managed to discover the complex numbers without ever learning about the real numbers, until they stumble upon some strange “fractal” objects in which we would recognise as real submanifolds, but which they are having a lot of difficulty understanding the geometry of with their purely complex methods. How would they begin to set up, say, the intersection theory of these objects?] But even here one has to be careful; intersection numbers of real manifolds, for instance, aren’t nearly as stable with respect to deformations as their complex counterparts (imagine perturbing two tangent circles, for instance). But presumably the real algebraic geometers have figured out all sorts of ways to deal with these sorts of issues, and perhaps some of those may extend to other well-behaved fractal settings. (For instance, one could start orienting these real manifolds to get signed intersections, but I have no idea how one would orient a more general fractal.)
which we would recognise as real submanifolds, but which they are having a lot of difficulty understanding the geometry of with their purely complex methods. How would they begin to set up, say, the intersection theory of these objects?] But even here one has to be careful; intersection numbers of real manifolds, for instance, aren’t nearly as stable with respect to deformations as their complex counterparts (imagine perturbing two tangent circles, for instance). But presumably the real algebraic geometers have figured out all sorts of ways to deal with these sorts of issues, and perhaps some of those may extend to other well-behaved fractal settings. (For instance, one could start orienting these real manifolds to get signed intersections, but I have no idea how one would orient a more general fractal.)
In response to one of Tim’s questions, though, I would say that this would be a “generalization for the fun of it”, at least until something non-trivial gets discovered…
21 May, 2009 at 2:04 pm
student
Dear Prof Tao,
is it possible to post your lectures in class to the web in the video lecture form?
some universities have opencourseware and they put some of their classes.
I think it would be perfect for the math community all over the world to watch your lectures online.
thanks
27 May, 2009 at 4:16 pm
Anonymous
Dear Prof. Tao,
It seems straightforward to generalize Hausdorff measure to non-Euclidean settings, say the p-adics, but are any such generalizations important?
More generally, I guess, what are some good applications of the study of Hausdorff dimension/measure to questions which do not seem at first to involve it? The Sobolev inequality you mentioned is a good example, but are there others? Maybe something connected in some way to Ratner’s theorems or dynamics/ergodic theory?
Thanks
29 May, 2009 at 7:47 am
Terence Tao
Dear anonymous,
I know that Hausdorff dimension plays a role in complex dynamics (indeed, many iconic examples of fractals, such as the Mandelbrot set, come from this field of mathematics), and also in random processes (Brownian motion, SLE, percolation, etc.), and have also made an appearance in other aspects of dynamical systems (e.g. Diophantine approximation), but I am not too familiar with these things. There is also a Hausdorff dimension-like notion for von Neumann algebras due to Voicolescu (though perhaps it is closer in some ways to Minkowski dimension) based on a non-commutative version of the metric entropy, but again I don’t know the details too well. As for the p-adics, I would imagine that metric methods such as Hausdorff dimension could theoretically be of use here, but the number-theoretic structure is much more powerful here than in the Euclidean setting and so the metric theory is likely to be overshadowed by the arithmetic one.
2 July, 2009 at 8:03 am
Confused
Sorry to ask but once in a while I happen to bump into both Hausdorff dimension and Hausdorff exponent in some papers on fractal and chaos. Is it the same thing?
Also curious, is the relations between Haudorff exponent and the power law exponent of the power spectrum is often confused with Hurst exponent… Does the Hausdorff exponent and the Hurst exponent define the same thing and meant the same thing?
21 July, 2010 at 4:30 am
Wolfgang M.
There appear to be four typo’s between definition 1 and exercise 1: some d’s should be alpha’s. Thanks for the post!
[Corrected, thanks – T.]
21 July, 2010 at 7:38 am
Wolfgang M.
Thanks for making the changes; but now there are too many alpha’s in there! =) [Oops, wasn’t paying enough attention. Fixed now – T.]
22 September, 2010 at 9:07 am
Snegud
Dear prof. Tao, ,
,  and
and  , then
, then  ,
,  and
and  (we take ball with centre at
(we take ball with centre at  )
)
There seems to be something wrong with second inequality in Exercise 4. If we take
[Corrected, thanks – T.]
18 May, 2011 at 10:44 am
Raina
Dear Prof. Tao,
I have just started reading about Hausdorff dimensions.
Let S in n-dimensional Euclidean Plane be a compact set of Hausdorff dimension t where 0<t<n is a non-integer. Let S-epsilon be the union of epsilon neighborhoods of all points in S. I could imagine a relation between the Lebesgue measure of S-epsilon and Hausdorff measure of S. But I could not think clearly. Is there any relation?
Could you suggest me books for reference (to read in detail about relation between Hausdorff measures and other(Borel,probability,Lebesgue) measures)?
18 May, 2011 at 12:00 pm
Terence Tao
Yes. See Exercises 15 and 16 of the above post.
As for references, I can recommend the books of Falconer and of Mattila.
18 May, 2011 at 11:56 pm
Raina
Thanks sir..
3 February, 2012 at 12:33 am
Rex
Typo: “…the dyadic and non-dyadic Huausdorff measures are comparable”
[Corrected, thanks-T.]
15 March, 2012 at 3:21 am
Raina
Is there any Co-area formula involving non integer Hausdorff dimension?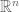 with Hausdorff dimension s
with Hausdorff dimension s  and
and  .
.
Moreover is it sensible to write the following:
Let S be a subset in
22 July, 2012 at 10:19 am
hamsi kafalı temel
prof tao I love you so much your real analysis notes are like a water in mohab desert
11 August, 2012 at 1:07 am
Anonymous
Small typo in the passage: “Let {0 \leq d \leq n}. Suppose {E} is a bounded portion of a {k}-dimensional subspace, e.g. {E = B^d(0,1) \times \{0\}^{n-d}}, where {B^d(0,1) \subset {\bf R}^d} is the unit ball in {{\bf R}^d} and we identify {{\bf R}^n} with {{\bf R}^d \times {\bf R}^{n-d}} in the usual manner.”
I believe the {k} here should be a {d}.
[Corrected, thanks – T.]
11 August, 2012 at 1:08 am
Rex
Whoops. My login seems to have failed…
18 August, 2012 at 9:05 am
Lucas Braune
You meant to write ‘prime’ instead of ‘maximal’ in the phrase “a chain of maximal ideals”.
[Corrected, thanks – T.]
20 August, 2012 at 5:50 am
Quora
What are the basic differences between physical and mathematical dimensions? And what are some uses, applications or examples of mathematical dimensions in the physical world?…
Terence Tao has a wonderful overview of the dimension concept [1]. Basically, there are several definitions of ‘dimension’ which we tend to use interchangeably because they give the same number in most cases. For instance determining the dimension by…
20 August, 2012 at 5:50 am
Dimensions: What are the basic differences between physical and mathematical dimensions? And what are some uses, applications or examples of mathematical dimensions in the physical world? - Quora
[…] of fractals. The sierpinski triangle for instance, has dimension 1.58. [1] https://terrytao.wordpress.com/20…"},"cls:a.app.view.components:BlurredAnswer:MgVYc2IwuP1/dH",{}), […]
12 April, 2013 at 4:37 pm
John Pearson
I believe that there are a couple of typos at the end of the proof of Lemma 3. At the end of the proof, I believe you should have
This allows you to conclude that which is what you want since you had shown
which is what you want since you had shown  in the lead-up to the lemma. (The inequalities were swapped in the version above.)
in the lead-up to the lemma. (The inequalities were swapped in the version above.)
[Corrected, thanks – T.]
20 May, 2014 at 4:27 pm
Sean Eberhard
Dear Terry,
I’ve noticed that many sources define Hausdorff measure somewhat differently in that they allow coverings by arbitrary sets U and then take the sum of the contributions (diam U)^s. Is this an important difference? I think it makes showing n-dim Hausdorff measure = Lebesgue measure more difficult. Is there any effect on applications?
Actually, is there much in the way of applications at all, or is Hausdorff dimension more of an end than a means? A hypothetical application would be, say, an existence proof which proceeds by showing that the set of desired objects has positive dimension.
20 May, 2014 at 7:29 pm
Terence Tao
The two definitions of Hausdorff dimension are equivalent, because any set U can be covered by a ball of diameter comparable to that of U. I suppose one could use the other definition of Hausdorff dimension if one wished to downplay the role of metric balls.
As for applications, Hausdorff dimension is often equal to other notions of dimension for “non-pathological” sets; for instance, for real algebraic varieties, the real algebraic dimension is equal to the Hausdorff dimension. So one can often use results about Hausdorff dimension to say something about other notions of dimension.
One can also use Hausdorff dimension to extract some topological information. For instance, suppose one removes a closed set from
from  . If all one knows about
. If all one knows about  is that it has measure zero, then this can disconnect
is that it has measure zero, then this can disconnect  ; consider for instance removing a hyperplane from
; consider for instance removing a hyperplane from  . But if one knows that
. But if one knows that  has Hausdorff dimension strictly less than
has Hausdorff dimension strictly less than 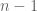 , one can show that the complement remains topologically path-connected (proof: given any two points
, one can show that the complement remains topologically path-connected (proof: given any two points  in the complement, connect them by line segments to a randomly selected third point
in the complement, connect them by line segments to a randomly selected third point  , and show that this almost surely avoids
, and show that this almost surely avoids  ). If
). If  has dimension strictly less than
has dimension strictly less than  , then the complement is also simply connected, and so forth. Several years ago, I used these facts with Gang Tian to show some singularity removal theorems for Yang-Mills fields, by first bounding the Hausdorff dimension of the singular set, and then exploiting the topological triviality of the complement as a consequence.
, then the complement is also simply connected, and so forth. Several years ago, I used these facts with Gang Tian to show some singularity removal theorems for Yang-Mills fields, by first bounding the Hausdorff dimension of the singular set, and then exploiting the topological triviality of the complement as a consequence.
11 June, 2014 at 6:49 am
Itay
Dear Prof. Tao,
I seem to be missing something. In the reformulation of upper and lower Minkowski dimension, it is not clear how does alpha play a role in the new formulation, and also maybe the volume should be the n-dimensional volume?
[Typos in post corrected, thanks – T.]
4 February, 2015 at 5:27 am
priya jain
Is there proof of exercise question????
21 March, 2015 at 5:08 pm
The Kakeya problem | Anurag's Math Blog
[…] Kakeya sets in have Hausdorff dimension equal to […]
24 April, 2015 at 5:51 am
Cyril
Dear Terry;
I’ve been try to answer this question for a very long time:
What can on say about Hausdorff dimension of a subfield of $\mathbb{R}$ ?
I have already built a proper uncountable subfield of $\mathbb{R}$ with null Hausdorff dimension but I don’t know there exists such subfields with not null Haussdorff dimension. Have you got any idea ?
Thanks a lot for the quality of your blog and the time you spend to answer questions of such beginners as I am.
24 April, 2015 at 10:54 am
Terence Tao
In the case of Borel-measurable subfields, the Hausdorff dimension must be either 0 or 1, a result of Edgar and Miller (answering a question of Erdos and Volkmann): http://www.ams.org/mathscinet-getitem?mr=1948103 . There is a more technical quantitative version of this, due to Bourgain, which has a number of important applications such as in the theory of expander graphs (and most recently, in the Kakeya problem): http://www.ams.org/mathscinet-getitem?mr=1982147
I don’t know what happens if the hypothesis of Borel measurability is dropped; the question may be sensitive to the axioms of set theory in the ambient mathematical universe.
24 April, 2015 at 5:47 pm
Mark Lewko
Hi Terry,
I’m curious what the “most recent” application of Bourgain’s ring theorem to the Kakeya problem is. I know in some non-rigorous / heuristic sense Bourgain’s theorem should imply the KLT $5/2+\epsilon$ result (based on, say, the BKT finite field argument) but I am not familiar with any literature on this.
24 April, 2015 at 6:17 pm
Terence Tao
This is extremely recent work of Katz and Zahl, which should appear on the arXiv in a few weeks. As you guessed, it gives a Hausdorff dimension bound of for Kakeya sets via a Euclidean version of the BKT argument.
for Kakeya sets via a Euclidean version of the BKT argument.
31 May, 2015 at 5:39 pm
Alan Chang
I think there is a typo in the second paragraph of section 1 (“Minkowski dimension”), in particular, in this sentence:
“These are open sets in {{\bf R}^n} and therefore have a {d}-dimensional volume (or Lebesgue measure) {\hbox{vol}^d(E_\delta)}.”
Should the two {d}’s be {n}’s?
[Corrected, thanks -T.]
15 April, 2016 at 2:06 am
245C, Notes 5: Hausdorff dimension (optional) | Alabair's Weblog
[…] Source : 245C, Notes 5: Hausdorff dimension (optional) […]
11 May, 2016 at 7:46 pm
Anonymous2
Does anybody happen to know where Minkowski gave his original work on “Minkowski dimension”?
12 May, 2016 at 5:47 pm
Anonymous
In Exercise 13, I think you mean ?
?
[Corrected, thanks – T.]
29 May, 2016 at 1:27 pm
Anonymous
By Lemma 3, one can find the -dimension Hausdorff measure of an
-dimension Hausdorff measure of an  -dimensional ball
-dimensional ball  . Do you have a hint how to find the (n-1)-dimension Hausdorff measure of the boundary
. Do you have a hint how to find the (n-1)-dimension Hausdorff measure of the boundary  ?
?
[Use Exercise 12 – T.]
17 June, 2016 at 4:20 pm
Anonymous
Hi Terry,
I think in equations both (4) and (5), there should be “log” in the numerator as well.
[Corrected, thanks – T.]
27 September, 2016 at 10:52 am
246A, Notes 2: complex integration | What's new
[…] is clarified once one develops the theory of Hausdorff dimension, as is done for instance in this previous post: any curve of Hausdorff dimension strictly greater than one will be […]
19 April, 2017 at 11:05 pm
Dominik
There is a typo in Lemma 4 (Frostman’s lemma). It should say “of dimension at most d” instead of “at least d”.
[Corrected, thanks – T.]
21 April, 2017 at 1:02 am
Dominik
Now its wrong in both Lemma 4 and Exercise 17. It should say “at most d”.
22 April, 2017 at 4:05 am
Dominik
Ok, now I see that it really should say “at least d”, because that’s what the condition in the definition of a Frostman measure means. So, it’s right now in Lemma 4 and Exercise 17, but still in the last line of the proof of Frostman’s lemma it says “at most d”.
[Corrected, thanks – T.]
12 October, 2017 at 1:00 pm
Anonymous
I think there are a few typos below definition 1
(e.g. the upper minkowski statement should have + \epsilon in it rather than a – \epsilon)
15 March, 2018 at 4:18 pm
The co-area formula exercise from Terry Tao’s blog | zulfahmed
[…] is an exercise from Terry’s blog on Hausdorff […]
9 November, 2018 at 1:38 am
Fedor Petrov
How do we get the sigma-additivity of the measure obtained in the proof of Frostman’s lemma (on the semiring of dyadic cubes)? Does it require some additional care on the greedy procedure?
21 November, 2018 at 12:08 pm
Terence Tao
The measure provided by the Riesz representation theorem is automatically sigma-additive. (Alternatively one could also argue using the Kolmogorov extension theorem.)
13 January, 2019 at 7:30 am
Anonymous
For exercise 9, if , then
, then

 then
then  ; this is weaker than the statement in Exercise 9. And it seems that the argument above does not exploit the special number
; this is weaker than the statement in Exercise 9. And it seems that the argument above does not exploit the special number  yet. Can you give a hint?
yet. Can you give a hint?
This shows that if
13 January, 2019 at 5:20 pm
Terence Tao
First show that any bounded subset of has finite
has finite  -dimensional Hausdorff outer measure.
-dimensional Hausdorff outer measure.
13 January, 2019 at 8:40 pm
Anonymous
Looks like Trick 6 in
One can show this by covering the bounded subset of with balls of a smaller radius. It then follows by the observation in the previous comment that
with balls of a smaller radius. It then follows by the observation in the previous comment that

for all bounded subsets. How to “patch things together”?
Without countably subadditive, how can one pass it to the unbounded case? (Stein-Shakarchi established subadditivity; one could look it up in the book. Can one do it alternatively?) Or does one have to establish some “continuity” of (which I don’t find a way to show) so that one can look at the Hausdorff outer measure of sets
(which I don’t find a way to show) so that one can look at the Hausdorff outer measure of sets  ?
?
(It’s interesting to look at different proofs. In Wolff’s notes that mentioned in the last sentence of this post, the author gave a mysterious one-sentence proof: “when , one can cover
, one can cover  by discs
by discs  with
with  arbitrarily small.”, which I have no ideas what he means.)
arbitrarily small.”, which I have no ideas what he means.)
14 January, 2019 at 8:41 am
Terence Tao
Use Trick 11 (combined with Trick 2).
13 January, 2019 at 4:58 pm
Arash
Hi, “this quantity is increasing in $r$”. Should not it be decreasing with $r$?
[Corrected, thanks – T.]
19 February, 2019 at 6:36 pm
Anonymous
Dear Prof. Tao,
In Exercise 20, the statement asserted to be equivalent to seems independent to the set
seems independent to the set  . It may be better to correct this statement.
. It may be better to correct this statement.
[Corrected, thanks – T.]
25 February, 2019 at 11:43 pm
Anonymous
Dear Prof. Tao,
I’m struggling with Exercise 21.(i). I don’t see how being small is used. I see directly that the lower Minkowski dimension of any set with positive
being small is used. I see directly that the lower Minkowski dimension of any set with positive  measure is greater or equal to
measure is greater or equal to  , but I guess the problem is treating covering by balls of varying radius.
, but I guess the problem is treating covering by balls of varying radius.
27 February, 2019 at 7:47 am
Terence Tao
The point is that if is a sequence of nonnegative numbers such that
is a sequence of nonnegative numbers such that  is large, then one must have
is large, then one must have  for some
for some  (pigeonhole principle). In this question, the numbers
(pigeonhole principle). In this question, the numbers  are basically the Frostman measure of the union of balls of radius equal (after rounding) to
are basically the Frostman measure of the union of balls of radius equal (after rounding) to  in a suitable covering of the set by balls of variable radius.
in a suitable covering of the set by balls of variable radius.
17 April, 2019 at 9:38 am
Anonymous
Dear prof. Tao.
I am having problem with exercise 5, especifically for the unbounded generalization of the definion of Minkowski dimension. Any hint? Thank you very much.
28 December, 2020 at 7:15 pm
yi
Dear prof. Tao : there seems to have a typo in here “We have {\overline{\hbox{dim}}_M(E) 0}, one has {\hbox{vol}^n(E_\delta) \leq C \delta^{n-\alpha-\epsilon}} for all sufficiently small {\delta > 0} and some {C > 0}”
[Corrected, thanks – T.]
16 May, 2023 at 7:13 am
Anonymous
Dear Professor Tao:
I have a question on the statement of Exercise 8, you said that for any $x_0\in X$, the inequality holds. However, in the inequality, the 1st term of right hand side is $\sup_{x_0\in E_0}f(x_0)$, so in fact, the $x_0$ in the statement is not used in the inequality(because you already take a supremum). Why do you say that for any $x_0\in X$?
[This was a typo, now corrected – T.]
2 February, 2024 at 12:54 am
Anonymous
I really liked that interpretation of the Hausdorff dimension of a set in terms of “its roughness”, because it is also what the Sobolev dimension of measures tells us. Do you also interpret the energies of the Fourier dimension spectrum as quantifying how smooth the measure is in terms of its fractional derivatives?
The energy I talk about is defined as:
I believe the integrals in Exercise 26 should be on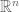 instead of
instead of 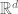 ?
?
[Erratum added, thanks. These energies can also be viewed as measures of regularity; this can be clarified by looking at Littlewood-Paley components of the measure. -T]