Previous set of notes: Notes 1. Next set of notes: Notes 3.
Having discussed differentiation of complex mappings in the preceding notes, we now turn to the integration of complex maps. We first briefly review the situation of integration of (suitably regular) real functions of one variable. Actually there are three closely related concepts of integration that arise in this setting:
- (i) The signed definite integral
, which is usually interpreted as the Riemann integral (or equivalently, the Darboux integral), which can be defined as the limit (if it exists) of the Riemann sums
whereis some partition of
,
is an element of the interval
, and the limit is taken as the maximum mesh size
goes to zero (this can be formalised using the concept of a net). It is convenient to adopt the convention that
for
; alternatively one can interpret
as the limit of the Riemann sums (1), where now the (reversed) partition
goes leftwards from
to
, rather than rightwards from
to
.
- (ii) The unsigned definite integral
, usually interpreted as the Lebesgue integral. The precise definition of this integral is a little complicated (see e.g. this previous post), but roughly speaking the idea is to approximate
by simple functions
for some coefficients
and sets
, and then approximate the integral
by the quantities
, where
is the Lebesgue measure of
. In contrast to the signed definite integral, no orientation is imposed or used on the underlying domain of integration, which is viewed as an “undirected” set
.
- (iii) The indefinite integral or antiderivative
, defined as any function
whose derivative
exists and is equal to
on
. Famously, the antiderivative is only defined up to the addition of an arbitrary constant
, thus for instance
.
There are some other variants of the above integrals (e.g. the Henstock-Kurzweil integral, discussed for instance in this previous post), which can handle slightly different classes of functions and have slightly different properties than the standard integrals listed here, but we will not need to discuss such alternative integrals in this course (with the exception of some improper and principal value integrals, which we will encounter in later notes).
The above three notions of integration are closely related to each other. For instance, if is a Riemann integrable function, then the signed definite integral and unsigned definite integral coincide (when the former is oriented correctly), thus
and
If is continuous, then by the fundamental theorem of calculus, it possesses an antiderivative
, which is well defined up to an additive constant
, and
for any , thus for instance
and
.
All three of the above integration concepts have analogues in complex analysis. By far the most important notion will be the complex analogue of the signed definite integral, namely the contour integral , in which the directed line segment from one real number
to another
is now replaced by a type of curve in the complex plane known as a contour. The contour integral can be viewed as the special case of the more general line integral
, that is of particular relevance in complex analysis. There are also analogues of the Lebesgue integral, namely the arclength measure integrals
and the area integrals
, but these play only an auxiliary role in the subject. Finally, we still have the notion of an antiderivative
(also known as a primitive) of a complex function
.
As it turns out, the fundamental theorem of calculus continues to hold in the complex plane: under suitable regularity assumptions on a complex function and a primitive
of that function, one has
whenever is a contour from
to
that lies in the domain of
. In particular, functions
that possess a primitive must be conservative in the sense that
for any closed contour. This property of being conservative is not typical, in that “most” functions
will not be conservative. However, there is a remarkable and far-reaching theorem, the Cauchy integral theorem (also known as the Cauchy-Goursat theorem), which asserts that any holomorphic function is conservative, so long as the domain is simply connected (or if one restricts attention to contractible closed contours). We will explore this theorem and several of its consequences in the next set of notes.
— 1. Integration along a contour —
The notion of a curve is a very intuitive one. However, the precise mathematical definition of what a curve actually is depends a little bit on what type of mathematics one wishes to do. If one is mostly interested in topology, then a good notion is that of a continuous (parameterised) curve. If one wants to do analysis in somewhat irregular domains, it is convenient to restrict the notion of curve somewhat, to the rectifiable curves. If one is doing analysis in “nice” domains (such as the complex plane , a half-plane, a punctured plane, a disk, or an annulus), then it is convenient to restrict the notion further, to the piecewise smooth curves, also known as contours. If one wished to get to the main theorems of complex analysis as quickly as possible, then one would restrict attention only to contours and skip much of this section; however we shall take a more leisurely approach here, discussing curves and rectifiable curves as well, as these concepts are also useful outside of complex analysis. In fact, we will structure our notes so that most of our theorems in fact apply to rectifiable curves (and several will in fact be applicable to arbitrary continuous curves).
We begin by defining the notion of a continuous curve.
Definition 1 (Continuous curves) A continuous parameterised curve, or curve for short, is a continuous map
from a compact interval
to the complex plane
. We call the curve trivial if
, and non-trivial otherwise. We refer to the complex numbers
as the initial point and terminal point (or final point) of the curve respectively, and refer to these two points collectively as the endpoints of the curve. We say that the curve is closed if
. We say that the curve is simple if one has
for any distinct
, with the possible exception of the endpoint cases
or
(thus we allow closed curves to be simple). We refer to the subset
of the complex plane as the image of the curve.
We caution that the term “closed” here does not refer to the topological notion of closure: for any curve (closed or otherwise), the image
of the curve, being the continuous image of a compact set, is necessarily a compact subset of
and is thus always topologically closed.
A basic example of a curve is the directed line segment from one complex point
to another
, defined by
for . (Thus, contrary to the informal English meaning of the terms, we consider line segments to be examples of curves, despite having zero curvature; in general, it is convenient in mathematics to admit such “degenerate” objects into one’s definitions, in order to obtain good closure properties for these objects, and to maximise the generality of the definition.) If
, this is a simple curve, while for
it is (a rather degenerate, but still non-trivial) closed curve. Another important example of a curve is the anti-clockwise circle
of some radius
around a complex centre
, defined by
This is a simple closed non-trivial curve. If we extended the domain here from to (say)
, the curve would remain closed, but would no longer be simple (every point in the image is now traversed twice by the curve).
Note that it is technically possible for two distinct curves to have the same image. For instance, the anti-clockwise circle of some radius
around a complex centre
defined by
traverses the same image as the previous curve (2), but is considered a distinct curve from . Nevertheless the two curves are closely related to each other, and we formalise this as follows. We say that one curve
is a continuous reparameterisation of another
, if there is a homeomorphism
(that is to say, a continuous invertible map whose inverse
is also continuous) which is endpoint preserving (i.e.,
and
) such that
for all
(that is to say,
, or equivalently
), in which case we write
. Thus for instance
. The relation of being a continuous reparameterisation is an equivalence relation, so one can talk about the notion of a curve “up to continuous reparameterisation”, by which we mean an equivalence class of a curve under this relation. Thus for instance the image of a curve, as well as its initial point and end point, are well defined up to continuous reparameterisation, since if
then
and
have the same image, the same initial point, and the same terminal point. It is common to depict an equivalence class of a curve
graphically, by drawing its image together with an arrow depicting the direction of motion from the initial point to its endpoint. (In the case of a non-simple curve, one may need multiple arrows in order to clarify the direction of motion, and also the possible multiplicity of the curve.)
Exercise 2 Let
be a continuous invertible map.
- (i) Show that
is continuous, so that
is a homeomorphism. (Hint: use the fact that a continuous image of a compact set is compact, and that a subset of an interval is topologically closed if and only if it is compact.)
- (ii) If
, show that
and that
is monotone increasing. (Hint: use the intermediate value theorem.)
- (iii) Conversely, if
is a continuous monotone increasing map with
and
, show that
is a homeomorphism.
It will be important for us that we do not allow reparameterisations to reverse the endpoints. For instance, if are distinct points in the complex plane, the directed line segment
is not a reparameterisation of the directed line segment
since they do not have the same initial point (or same terminal point); the map
is a homeomorphism from
to
but it does not preserve the initial point or the terminal point. In general, given a curve
, we define its reversal
to be the curve
, thus for instance
is (up to reparameterisation) the reversal of
, thus
Another basic operation on curves is that of concatenation. Suppose we have two curves and
with the property that the terminal point
of
equals the initial point
of
. We can reparameterise
by translation to
, defined by
. We then define the concatenation or sum
by setting
for and
for (note that these two definitions agree on their common domain point
by the hypothesis
. It is easy to see that this concatenation
is still a continuous curve. The reader at this point is encouraged to draw a picture to understand what the concatenation operation is doing; it is much simpler to grasp it visually than the above lengthy definition may suggest. If the terminal point of
does not equal the initial point of
, we leave the sum
undefined. (One can define more general spaces than the space of curves in which such an addition can make sense, such as the space of
-currents if one assumes some rectifiability on the curves, or the space of
-chains, but we will not need such general spaces here.)
Concatenation is well behaved with respect to equivalence and reversal:
Exercise 3 Let
be continuous curves. Suppose that the terminal point of
equals the initial point of
, and the terminal point of
equals the initial point of
.
- (i) (Concatenation and reversal well defined up to equivalence) If
and
, show that
and
.
- (ii) (Concatenation associative) Show that
. In particular, we certainly have

- (iii) (Concatenation and reversal) Show that
.
- (iv) (Non-commutativity) Give an example in which
and
are both well-defined, but not equivalent to each other.
- (v) (Identity) If
and
denote the initial and terminal points of
respectively, and
is the trivial curve
defined for any
, show that
and
.
- (vi) (Non-invertibility) Give an example in which
is not equivalent to a trivial curve. (It will however be homologous to a trivial curve, as we will discuss in later notes.)
Remark 4 The above exercise allows one to view the space of curves up to equivalence as a category, with the points in the complex plane being the objects of the category, and each equivalence class of curves being a single morphism from the initial point to the terminal point (and with the equivalence class of trivial curves being the identity morphisms). This point of view can be useful in topology, particularly when relating to concepts such as the fundamental group (and fundamental groupoid), monodromy, and holonomy. However, we will not need to use any advanced category-theoretic concepts in this course.
Exercise 5 Let
and
. For any integer
, let
denote the curve
(thus for instance
).
- (i) Show that for any integer
, we have
.
- (ii) Show that for any non-negative integers
, we have
. What happens for other values of
?
- (ii) If
are distinct integers, show that
.
Given a sequence of complex numbers , we define the polygonal path
traversing these numbers in order to be the curve
This is well-defined thanks to Exercise 3(ii) (actually all we really need in applications is being well-defined up to equivalence). Thus for instance would traverse a closed triangular path connecting
,
, and
(this path may end up being non-simple if the points
are collinear).
In order to do analysis, we need to restrict our attention to those curves which are rectifiable:
Definition 6 Let
be a curve. The arc length
of the curve is defined to be the supremum of the quantities
where
ranges over the natural numbers and
ranges over the partitions of
. We say that the curve
is rectifiable if its arc length is finite.
The concept is best understood visually: a curve is rectifiable if there is some finite bound on the length of polygonal paths one can form while traversing the curve in order. From Exercise 2 we see that equivalent curves have the same arclength, so the concepts of arclength and rectifiability are well defined for curves that are only given up to continuous reparameterisation.
Exercise 7 Let
be curves, with the terminal point of
equal to the initial point of
. Show that
In particular,
is rectifiable if and only if
are both individually rectifiable.
It is not immediately obvious that any reasonable curve (e.g. the line segments or the circles
) are rectifiable. To verify this, we need two preliminary results.
Lemma 8 (Triangle inequality) Let
be a continuous function. Then
Here we interpret
as the Riemann integral (or equivalently,
).
Proof: We first attempt to prove this inequality by considering the real and imaginary parts separately. From the real-valued triangle inequality (and basic properties of the Riemann integral) we have
and similarly
but these two bounds only yield the weaker estimate
To eliminate this loss we can amplify the above argument by exploiting phase rotation. For any real
, we can repeat the above arguments (using the complex linearity of the Riemann integral, which is easily verified) to give
But we have for any complex number
, so taking the supremum of both sides in
we obtain the claim.
Exercise 9 Let
be real numbers. Show that the interval
is topologically connected, that is to say the only two subsets of
that are both open and closed relative to
are the empty set and all of
. (Hint: if
is a non-empty set that is both open and closed in
and contains
, consider the supremum of all
such that
.)
Next, we say that a non-trivial curve is continuously differentiable if the derivative
exists and is continuous for all (note that we are only taking right-derivatives at
and left-derivatives at
).
Proposition 10 (Arclength formula) If
is a continuously differentiable curve, then it is rectifiable, and
Proof: We first prove the upper bound
which in particular implies the rectifiability of since the right-hand side of (3) is finite. Let
be any partition of
. By the fundamental theorem of calculus (applied to the real and imaginary parts of
) we have
for any , and hence by Lemma 8 we have
Summing in we obtain
and taking suprema over all partitions we obtain (3).
Now we need to show the matching lower bound. Let be a small quantity, and for any
, let
denote the restriction of
to
. We will show the bound
for all ; specialising to
and then sending
will give the claim.
It remains to prove (4) for a given choice of . We will use a continuous version of induction known as the continuity method, which exploits Exercise 9.
Let denote the set of
such that (4) holds for all
. It is clear (using Exercise 7, which implies that
is an increasing function of
) that this set
is topologically closed, and also contains the left endpoint
of
. If
and
, then from the differentiability of
at
, we have some interval
such that
for all . Rearranging this using the triangle inequality, we have
Also, from the continuity of we have
for all , if
is small enough. We conclude that
and hence
where is the restriction of
to
. Adding this to the
case of (4) using Exercie 7 we conclude that (4) also holds for all
. From this we see that
is (relatively) open in
; from the connectedness of
we conclude that
, and we are done.
It is now easy to verify that the line segment is rectifiable with arclength
, and that the circle
is rectifiable with arclength
, exactly as one would expect from elementary geometry. Finally, from Exercise 7, a polygonal path
will be rectifiable with arclength
, again exactly as one would expect.
Exercise 11 Show that the curve
defined by setting
for
and
is continuous but not rectifiable. (Hint: it is not necessary to compute the arclength precisely; a lower bound that goes to infinity will suffice. Graph the curve to discover some convenient partitions with which to generate such lower bounds. Alternatively, one can apply the arclength formula to some subcurves of
.)
Exercise 12 (This exercise presumes familiarity with Lebesgue measure.) Show that the image of a rectifiable curve is necessarily of measure zero in the complex plane. (In particular, space-filling curves such as the Peano curve or the Hilbert curve cannot be rectifiable.)
Remark 13 As the above exercise suggests, many fractal curves will fail to be rectifiable; for instance the Koch snowflake is a famous example of an unrectifiable curve. (The situation is clarified once one develops the theory of Hausdorff dimension, as is done for instance in this previous post: any curve of Hausdorff dimension strictly greater than one will be unrectifiable.)
Exercise 14 (Arclength parameterisation) Let
be a rectifiable curve.
- (i) Show that the arclength of the restriction of
to
for
varies continuously in
. (Hint: you may find it convenient to first establish the preliminary bound
for any
and
, and similarly
for any
.)
- (ii) Assume furthermore that
is not constant on any time interval of positive length. Show that there exists a unique reparameterisation
with the property that for each
, the restriction of
to
has arclength exactly
.
Much as continuous functions on an interval may be integrated by taking limits of Riemann sums, we may also integrate continuous functions
on the image of a rectifiable curve
:
Proposition 15 (Integration in rectifiable curves) Let
be a rectifiable curve, and let
be a continuous function on the image
of
. Then the “Riemann sums”
where
ranges over the partitions of
, and for each
,
is an element of
, converge as the maximum mesh size
goes to zero to some complex limit, which we will denote as
. In other words, for every
there exists a
such that
whenever
.
Proof: In real analysis courses, one often uses the order properties of the real line to replace the rather complicated looking Riemann sums with the simpler Darboux sums, en route to proving the real-variable analogue of the above proposition. However, in our complex setting the ordering of the real line is not available, so we will tackle the Riemann sums directly rather than try to compare them with Darboux sums.
It suffices to prove that the “Riemann sums” (5) are a Cauchy sequence (or more precisely a Cauchy net), in the sense that the difference
between two sums of the form (5) is smaller than any specified if the maximum mesh sizes of the two partitions
and
are both small enough. From the triangle inequality, and from the fact that any two partitions have a common refinement, it suffices to prove this under the additional assumption that the second partition
is a refinement of
. This means that there is an increasing sequence
of natural numbers such that
for
. In that case, the above difference may be rearranged as
where
By telescoping series, we may rearrange further as
As is continuous and
is compact,
is uniformly continuous. In particular, if the maximum mesh sizes are small enough, we have
for all and
. From the triangle inequality we conclude that
and hence on summing in and using the triangle inequality, we can bound
Since is finite, and
can be made arbitrarily small, we obtain the required Cauchy net property.
One cannot simply omit the rectifiability hypothesis from the above proposition:
Exercise 16 Give an example of a curve
such that the Riemann sums
fail to converge to a limit as the maximum mesh size goes to zero, so the integral
does not exist in the sense of convergent Riemann sums even though the integrand
is extremely smooth. (Of course, such a curve
cannot be rectifiable, thanks to Proposition 15.) Hint: the non-rectifiable curve in Example 11 is a good place to start, but it turns out that this curve does not oscillate wildly enough to make the Riemann sums here diverge, because of the decay of the function
near the origin. Come up with a variant of this curve which oscillates more. Nevertheless, it is still possible to assign a meaning to integrals such as
, as we shall see in the next set of notes once Cauchy’s theorem is established.
By abuse of notation, we will refer to the quantity as the contour integral of
along
, even though
is not necessarily a contour (we will define this concept shortly). We have some easy properties of this integral:
Exercise 17 Let
be a rectifiable curve, and
be a continuous function.
- (i) (Independence of parameterisation) If
is another curve equivalent to
, show that
.
- (ii) (Reversal) Show that
.
- (iii) (Concatenation) If
for some curves
, show that
- (iv) (Change of variables) If
is continuously differentiable, show that
- (v) (Upper bound) If there is a pointwise bound of the form
for all
and some
, show that
- (vi) (Linearity) If
is a complex number and
is a continuous function, show that
and
- (vii) (Integrating a constant) If
has initial point
and terminal point
, show that
- (viii) (Uniform convergence) If
,
is a sequence of continuous functions converging uniformly to
as
, show that
converges to
as
. (The requirement of uniform convergence can be relaxed substantially, thanks to tools such as the dominated convergence theorem, but this weaker convergence theorem will suffice for most of our applications.)
- (ix) (Change of variables, II) Let
be an open neighbourhood of
, let
be a holomorphic function, and let
be a continuous function. Show that
is rectifiable, and
(For this question, you may assume without proof that holomorphic functions are continuously differentiable; this fact will be proven (without reliance on this part of the exercise) in the next set of notes.)
Exercise 18 (This exercise assumes familiarity with the Riemann-Stieltjes integral.) Let
be a rectifiable curve. Let
denote the monotone non-decreasing function
for
, where
is the restriction of
to
. For any continuous function
, define the arclength measure integral
by the formula
where the right-hand side is a Riemann-Stieltjes integral. Establish the triangle inequality
for any continuous
. Also establish the identity
and obtain an alternate proof of Exercise 17(v).
The change of variables formula (iv) lets one compute many contour integrals using the familiar Riemann integral. For instance, if are real numbers and
is continuous, then the contour integral along
coincides with the Riemann integral,
and on reversal we also have
Similarly, if is continuous on the circle
, we have
Remark 19 We caution that if
is real-valued, we cannot conclude that
is also real valued, unless the contour
lies in the real line. This is because the complex line element
may introduce some non-trivial imaginary part, as is the case for instance in (6). For similar reasons, we have
and
in general. If one wishes to mix line integrals with real and imaginary parts, it is recommended to replace the contour integrals above with the line integrals
which are defined as in Proposition 15 but where the expression
appearing in (5) is replaced by
The contour integral corresponds to the special case
(or more informally,
). Line integrals are in turn special cases of the more general concept of integration of differential forms, discussed for instance in this article of mine, and which are used extensively in differential geometry and geometric topology. However we will not use these more general line integrals or differential form integrals much in this course.
In later notes it will be convenient to restrict to a more regular class of curves than the rectifiable curves. We thus give the definitions here:
Definition 20 (Smooth curves and contours) A smooth curve is a curve
that is continuously differentiable, and such that
for all
. A contour is a curve that is equivalent to the concatenation of finitely many smooth curves (that is to say, a piecewise smooth curve).
Example 21 The line segments
and circles
are smooth curves and hence contours. Polygonal paths are usually not smooth, but they are contours. Any sum of finitely many contours is again a contour, and the reversal of a contour is also a contour.
Note here that the term “smooth” differs somewhat here from the real-variable notion of smoothness, which is defined to be “infinitely differentiable”. Smooth curves are still only assumed to just be continuously differentiable; we do not assume that the second derivative of exists. (In particular, smooth curves may have infinite curvature at some points.) In practice, this distinction tends to be minor, though, as the smooth curves that one actually uses in complex analysis do tend to be infinitely differentiable. On the other hand, for most applications one does not need to control any derivative of a contour beyond the first.
The following examples and exercises may help explain why the non-vanishing condition imbues curves with a certain degree of “smoothness”.
Example 22 (Cuspidal curve) Consider the curve
defined by
. Clearly
is continously differentiable (and even infinitely differentiable), but we do not view this curve as smooth, because
vanishes at the origin. Indeed, the image of the curve is
, which looks visibly non-smooth at the origin if one plots it, due to the presence of a cusp.
Example 23 (Absolute value function) Consider the curve
defined by
. This curve is certainly continuously differentiable, and in fact is four times continuously differentiable, but is not smooth because
vanishes at the origin. The image of this curve is
, which looks visibly non-smooth at the origin (in particular, there is no unique tangent line to this curve here).
Example 24 (Spiral) Consider the curve
defined by
for
, and
. One can check (exercise!) that
is continuously differentiable, even at the origin
; but it is not a smooth curve because
vanishes. The image of
has some rather complicated behaviour at the origin, for instance it intersects itself multiple times (try to sketch it!).
Exercise 25 (Local behaviour of smooth curves) Let
be a simple smooth curve, and let
be an interior point of
. Let
be a phase of
, thus
for some
. Show that for all sufficiently small
, the portion
of the image of
near
looks like a rotated graph, in the sense that
for some interval
containing the origin, and some continuously differentiable function
with
. Furthermore, show that
as
(or equivalently, that
as
). (Hint: you may find it easier to first work with the model case where
and
. The real-variable inverse function theorem will also be helpful.)
Exercise 26 Show that a curve
is a contour if and only if it is equivalent to the concatenation of finitely many simple smooth curves.
Exercise 27 Show that the cuspidal curve and absolute value curves in Examples 22, 23 are contours, but the curve in Exercise 24 is not.
— 2. The fundamental theorem of calculus —
Now we establish the complex analogues of the fundamental theorem of calculus. As in the real-variable case, there are two useful formulations of this theorem. Here is the first:
Theorem 28 (First fundamental theorem of calculus) Let
be an open subset of
, let
be a continuous function, and suppose that
has an antiderivative
, that is to say a holomorphic function with
for all
. Let
be a rectifiable curve in
with initial point
and terminal point
. Then
Proof: If were continuously differentiable, or at least piecewise continuously differentiable (the concatenation of finitely many continuously differentiable curves), we could establish this theorem by using Exercise 17 to rewrite everything in terms of real-variable Riemann integrals, at which point one can use the real-variable fundamental theorem of calculus (and the chain rule). But actually we can just give a direct proof that does not need any differentiability hypothesis whatsoever.
We again use the continuity method. Let , and for each
, let
be the restriction of
to
. It will suffice to show that
for all , as the claim then follows by setting
and sending
to zero.
Let denote the set of all
such that (7) holds for all
. As before,
is clearly closed and contains
; as
is connected, the only remaining task is to show that
is open in
. Let
be such that
. As
is differentiable at
with derivative
, and
is continuous, there exists
with
such that
for any . On the other hand, if
is small enough, we have that
for all , and hence by Exercise 17(v) we have
where is the restriction of
to
. Applying Exercise 17(vi), (vii) we thus have
Combining this with (8) and the triangle inequality, we conclude that
and on adding this to the case of (7) and again using the triangle inequality, we conclude that (7) holds for all
. This ensures that
is open, as desired.
One can use this theorem to quickly evaluate many integrals by using an antiderivative for the integrand as in the real-variable case. For instance, for any rectifiable curve with initial point
and terminal point
, we have
and so forth. If the curve avoids the origin, we also have
since is an antiderivative of
on
. If
is a power series with radius of convergence
, and
is a rectifiable curve in
with initial point
and terminal point
, we similarly have
For the second fundamental theorem of calculus, we need a topological preliminary result.
Exercise 29 Let
be a non-empty open subset of
. Show that the following statements are equivalent:
- (i)
is topologically connected (that is to say, the only two subsets of
that are both open and closed relative to
are the empty set and
itself).
- (ii)
is path connected (that is to say, for any
there exists a curve
with image in
whose initial point is
and terminal point is
).
- (iii)
is polygonally path connected (the same as (ii), except that
is now required to also be a polygonal path).
(Hint: to show that (i) implies (iii), pick a base point
in
and consider the set of all
in
that can be reached from
by a polygonal path.)
We remark that the relationship between path connectedness and connectedness is more delicate when one does not assume that the space is open; every path-connected space is still connected, but the converse need not be true.
Remark 30 There is some debate as to whether to view the empty set
as connected, disconnected, or neither. I view this as analogous to the debate as to whether the natural number
should be viewed as prime, composite, or neither. In both cases I personally prefer the convention of “neither” (and like to use the term “unconnected” to describe the empty set, and “unit” to describe
), but to avoid any confusion I will restrict the discussion of connectedness to non-empty sets in this course (which is all we will need in applications).
In real analysis, the second fundamental theorem of calculus asserts that if a function is continuous, then the function
is an antiderivative of
. In the complex case, there is an analogous result, but one needs the additional requirement that the function is conservative:
Theorem 31 (Second fundamental theorem of calculus) Let
be a non-empty open connected subset of the complex numbers. Let
be a continuous function which is conservative in the sense that
whenever
is a closed polygonal path in
. Fix a base point
, and define the function
by the formula
for all
, where
is any polygonal path from
to
in
(the existence of such a path follows from Exercise 29 and the hypothesis that
is connected, and the independence of the choice of path for the purposes of defining
follows from Exercise 17 and the conservative hypothesis (9)). Then
is holomorphic on
and is an antiderivative of
, thus
for all
.
Proof: We mimic the proof of the real-variable second fundamental theorem of calculus. Let be any point in
. As
is open, it contains some disk
centred at
. In particular, if
lies in this disk, then the line segment
will have image in
. If
is any polygonal path from
to
, then we have
and
and hence by Exercise 17
(The reader is strongly advised to draw a picture depicting the situation here.) Let , then for
sufficiently close to
, we have
for all
in the image of
. Thus by Exercise 17(v) we have
for sufficiently close to
, which implies that
for any , and thus
is an antiderivative of
as required.
The notion of a non-empty open connected subset of the complex plane comes up so frequently in complex analysis that many texts assign a special term to this notion; for instance, Stein-Shakarchi refers to such sets as regions, and in other texts they may be called domains. We will stick to just “non-empty open connected subset of
” in this course.
The requirement that be conservative is necessary, as the following exercise shows. Actually it is also necessary in the real-variable case, but it is redundant in that case due to the topological triviality of closed polygonal paths in one dimension: see Exercise 34 below.
Exercise 32 Let
be a non-empty connected open subset of
, and let
be continuous. Show that the following are equivalent:
- (i)
possesses at least one antiderivative
.
- (ii)
is conservative in the sense that (9) holds for all closed polygonal paths in
.
- (iii)
is conservative in the sense that (9) holds for all simple closed polygonal paths in
.
- (iv)
is conservative in the sense that (9) holds for all closed contours in
.
- (v)
is conservative in the sense that (9) holds for all closed rectifiable curves in
.
(Hint: to show that (iii) implies (ii), induct on the number of edges in the closed polygonal path, and find a way to decompose non-simple closed polygonal paths into paths with fewer edges. One should avoid non-rigorous “hand-waving” arguments, and make sure that one actually has covered all possible cases, e.g. paths that include some backtracking.) Furthermore, show that if
has two antiderivatives
, then there exists a constant
such that
.
Exercise 33 Show that the function
does not have an antiderivative on
. (Hint: integrate
on
.) In later notes we will see that
nevertheless does have antiderivatives on many subsets of
, formed by various branches of the complex logarithm.
Exercise 34 If
is a continuous function on an interval, show that
is conservative in the sense that (9) holds for any closed polygonal path in
. What happens for closed rectifiable paths?
Exercise 35 Let
be an open subset of
(not necessarily connected).
- (i) Show that there is a unique collection
of non-empty subsets of
that are open, connected, disjoint, and partition
:
. (The elements of
are known as the connected components of
.)
- (ii) Show that the number of connected components of
is at most countable. (Hint: show that each connected component contains at least one complex number with rational real and imaginary parts.)
- (iii) If
is a continuous conservative function on
, show that
has at least one antiderivative
.
- (iv) If
has more than one connected component, show that it is possible for a function
to have two antiderivatives
which do not differ by a constant (i.e. there is no complex number
such that
).
Exercise 36 (Integration by parts) Let
be holomorphic functions on an open set
, and let
be a rectifiable curve in
with initial point
and terminal point
. Prove that
Note: the exercise below will be moved to a more logical location after the conclusion of the course.
Exercise 37 Let
be a curve. Show that the arclength
is the limit (in the extended real line) of the path lengths
, where
is a partition of
and the mesh size
goes to zero. In other words, if
is finite, show that for every
there exists
such that
whenever
, and when
is infinite, show that for every
there exists
such that
whenever
.

103 comments
Comments feed for this article
21 October, 2020 at 1:30 pm
Anonymous
1.
One can identify what is going on here by rewriting the RHS:
2.
By the definition of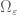 , (4) follows. Recall that in order to prove the proposition, we want to prove (3) and (4).
, (4) follows. Recall that in order to prove the proposition, we want to prove (3) and (4).
25 October, 2020 at 8:02 am
Anonymous
Can a simple curve be equivalent to a non-simple curve up to continuous reparameterisation?
On the one hand, it seems yes by considering (2) with the domains![[0,2\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5Cpi%5D&bg=ffffff&fg=545454&s=0&c=20201002) and
and ![[0,4\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C4%5Cpi%5D&bg=ffffff&fg=545454&s=0&c=20201002) , and the homomorphism
, and the homomorphism 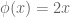 between these two closed intervals. On the other hand, we don’t want (do we?) these two curves to be equivalent since they have different winding numbers. Am I missing something?
between these two closed intervals. On the other hand, we don’t want (do we?) these two curves to be equivalent since they have different winding numbers. Am I missing something?
25 October, 2020 at 4:23 pm
Terence Tao
The reparameterisation of (2) using the change of variables is
is 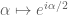 ,
,  , which continues to wind around the origin exactly once.
, which continues to wind around the origin exactly once.
25 October, 2020 at 4:38 pm
Anonymous
(Sorry for messing up the LaTeX code.)
I meant to ask that if the curve
![\displaystyle \gamma_1(\theta)=re^{i\theta},\quad \theta\in[0,2\pi]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cgamma_1%28%5Ctheta%29%3Dre%5E%7Bi%5Ctheta%7D%2C%5Cquad+%5Ctheta%5Cin%5B0%2C2%5Cpi%5D++&bg=ffffff&fg=545454&s=0&c=20201002)
![\displaystyle \gamma_2(\theta)=re^{i\theta},\quad \theta\in[0,4\pi]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cgamma_2%28%5Ctheta%29%3Dre%5E%7Bi%5Ctheta%7D%2C%5Cquad+%5Ctheta%5Cin%5B0%2C4%5Cpi%5D++&bg=ffffff&fg=545454&s=0&c=20201002)
and the curve
are equivalent up to continuous reparameterisation or not.
So the second one wind around the origin twice.
Is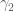 a reparameterisation of
a reparameterisation of  ?
?
[No. For instance, the arclengths are different. – T.]
25 October, 2020 at 5:25 pm
Anonymous
Ah, thanks. I confused myself with the definition. The homomorphism![\phi:[0,2\pi]\to[0,4\pi]](https://s0.wp.com/latex.php?latex=%5Cphi%3A%5B0%2C2%5Cpi%5D%5Cto%5B0%2C4%5Cpi%5D&bg=ffffff&fg=545454&s=0&c=20201002) with
with  would not work since
would not work since  .
.
25 October, 2020 at 2:12 pm
Anonymous
In the proof of Proposition 10,
… Adding this to the
I think “(7)” should be “Exercise 7”. Typo?
[Corrected, thanks – T.]
27 October, 2020 at 9:17 am
Wan-Teh Chang
Hi Prof. Tao,
I’d like to report some typos and suggest some minor edits in Notes 2.
In the sentence “We will explore this theorem and several of its consequences the next set of notes”, I suggest adding the word “in” before “the next set of notes”.
In Exercise 3 (i), “Concatenation well defined up to equivalence”, I suggest adding “and reversal” after “Concatenation”.
In Exercise 5 (i), “Show that for any integer “, remove “,
“, remove “,  “.
“.
In Definition 6, the subscripts in the summand are off by one. The subscripts in the summand should be and
and  , not
, not  and
and  .
.
At the end of the proof of Lemma 8 (Triangle inequality), “so taking the supremum of both sides in “, it suffices to take the supremum of the left-hand side because the right-hand side (a constant) is an upper bound of the left-hand side, and the supremum is
“, it suffices to take the supremum of the left-hand side because the right-hand side (a constant) is an upper bound of the left-hand side, and the supremum is  any upper bound. Note: It also suffices to pick a particular value of
any upper bound. Note: It also suffices to pick a particular value of  to make the left-hand side a nonnegative real number.
to make the left-hand side a nonnegative real number.
In the proof of Proposition 10 (Arclength formula), “for any “, change
“, change  to
to  .
.
In the proof of Proposition 10 (Arclength formula), in the inequality after “Summing in we obtain”, the indexes in the summand on the left-hand side should be
we obtain”, the indexes in the summand on the left-hand side should be  and
and  , not
, not  and
and  .
.
In Proposition 14 (Integration in rectifiable curves), the last sentence “In other words, for every there exists a
there exists a  such that”, I suggest adding “
such that”, I suggest adding “ ” after “
” after “ .
.
In Exercise 26, “but the curve in Exercise 23 is not”, change “Exercise” to “Example”.
Optional: In the proof of Theorem 27 (First fundamental theorem of calculus), the variable is generally used to denote a number in the closed interval
is generally used to denote a number in the closed interval ![[T_{*}, T_{*} + \delta]](https://s0.wp.com/latex.php?latex=%5BT_%7B%2A%7D%2C+T_%7B%2A%7D+%2B+%5Cdelta%5D&bg=ffffff&fg=545454&s=0&c=20201002) . However, in the sentence “On the other hand, if
. However, in the sentence “On the other hand, if  is small enough, we have that …”, the variable
is small enough, we have that …”, the variable  is used instead (two occurrences). It would be good to use the variable
is used instead (two occurrences). It would be good to use the variable  consistently.
consistently.
In the second-to-last sentence before Exercise 28, “…, and is a curve in
is a curve in  with initial point
with initial point 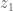 and terminal point
and terminal point 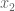 “, should we add “rectifiable” before “curve”?
“, should we add “rectifiable” before “curve”?
In the hypothesis of Exercise 31, “Let be a non-empty connected subset of
be a non-empty connected subset of  “, does
“, does  ” need to be open?
” need to be open?
In Exercise 34 (i), there is an uncommon symbol that looks like the set union operator with a sign inside. Is that a typo?
sign inside. Is that a typo?
Thank you!
[Thanks for the corrections. I use in the proof of Theorem 27 to distinguish it from
in the proof of Theorem 27 to distinguish it from  in the next line which will refer to a distinct time variable.
in the next line which will refer to a distinct time variable.  is the symbol for disjoint union. -T]
is the symbol for disjoint union. -T]
23 November, 2020 at 2:47 pm
Anonymous
I recall that you called the “continuity method” some sort of induction.
One version of the continuous induction says the following:
If and
and
(1)
 then there exists
then there exists 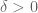 such that
such that 
 then
then  .
.
(2) if
(3) if
Then .
.
Is the “continuity method” linked in this note the same as the notion of “continuous induction”?
26 November, 2020 at 11:33 am
Terence Tao
This is one instance of the continuity method (using the fact that the half-line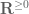 is connected with respect to the right half-open topology). More generally, the continuity method can be applied to arbitrary connected topological spaces (not just the half-line); in particular in this course we frequently apply it to open connected subsets of the complex plane.
is connected with respect to the right half-open topology). More generally, the continuity method can be applied to arbitrary connected topological spaces (not just the half-line); in particular in this course we frequently apply it to open connected subsets of the complex plane.
12 December, 2020 at 8:26 am
Anonymous
Is the continuity method related to (and can it be phrased as) transfinite induction?
12 December, 2020 at 11:22 am
Terence Tao
When one applies the continuity method to a totally ordered connected domain such as an interval, one can usually use transfinite induction (or Zorn’s lemma) as a substitute for the method. However the continuity method can also be applied to other connected domains (e.g., open connected subsets of the complex plane), for which it is less evident how to apply transfinite induction (though in many cases one could take advantage of path connectedness and apply transfinite induction along each path separately).
28 November, 2020 at 3:33 pm
Anonymous
If one considers continuous curves but only differentiable reparametrisations, would one loose anything?
28 November, 2020 at 4:38 pm
Anonymous
If![\gamma_1:[a_1,b_1]\to{\bf C}](https://s0.wp.com/latex.php?latex=%5Cgamma_1%3A%5Ba_1%2Cb_1%5D%5Cto%7B%5Cbf+C%7D&bg=ffffff&fg=545454&s=0&c=20201002) is equivalent to
is equivalent to ![\gamma_2:[a_2,b_2]\to{\bf C}](https://s0.wp.com/latex.php?latex=%5Cgamma_2%3A%5Ba_2%2Cb_2%5D%5Cto%7B%5Cbf+C%7D&bg=ffffff&fg=545454&s=0&c=20201002) up to continuous reparametrisation, i.e.,
up to continuous reparametrisation, i.e.,  for some endpoint preserving
for some endpoint preserving 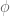 , is such
, is such 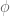 unique? If not, can one always find a
unique? If not, can one always find a 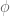 that is differentiable?
that is differentiable?
29 November, 2020 at 1:54 pm
Anonymous
It is not unique. One can always find one that is differentiable.
30 November, 2020 at 1:55 pm
Anonymous
Would it be circular somewhere if one uses Theorem 27 to prove Exercise 16(vii)?
[Probably, and in any event Theorem 27 is only applicable to holomorphic functions whereas Exercise 16 only requires continuity of the integrand. -T]
27 September, 2021 at 9:00 am
246A, Notes 1: complex differentiation | What's new
[…] Previous set of notes: Notes 0. Next set of notes: Notes 2. […]
8 April, 2022 at 7:44 am
J
… The contour integral can be viewed as the special case of the more general *line integral*
The linked Wikipedia article to “line integral” seems a bit confusing. In that article, “complex line integral” refers to the notion of “contour integrals” in this set of notes. On the other hand, they only define the line integral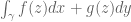 when
when  and
and  are both real-valued; that’s what they call the line integral for (real) vector fields. Any other references?
are both real-valued; that’s what they call the line integral for (real) vector fields. Any other references?
According to your PCM article on differential forms linked in this note, the Euclidean structure (dot product) is not needed in the integrals of differential forms, particularly the line integrals. Since the contour integral can be viewed as a special line integral, is it also “independent” of the metric structure of paths in the complex plane? But this would seem to contradict the discussion of rectifiable curves where a metric is needed.
10 April, 2022 at 8:53 pm
Terence Tao
One can define line integrals for complex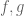 simply by computing the real and imaginary parts of the integral separately, much as one can compute the Riemann integral of a complex function in terms of the Riemann integral of the real and imaginary parts.
simply by computing the real and imaginary parts of the integral separately, much as one can compute the Riemann integral of a complex function in terms of the Riemann integral of the real and imaginary parts.
Rectificability only needs the metric structure up to Lipschitz equivalence; the Euclidean metric can be replaced by any other Lipschitz equivalent metric and one still has the same notion of rectifiability. Because all norms on a finite dimensional vector space are equivalent, the notion of rectifiability thus does not require any specific metric structure on this space.
9 April, 2022 at 8:16 pm
Anonymous
[Corrected, thanks – T.]
24 April, 2022 at 5:01 am
N is a number
Professor Tao, you have mentioned the terms “signed definite integral” and “unsigned integral” quite a few times in different contexts, and here too you started by stating these while reviewing the notions of integration one has for a real-valued function![f: [ a,b] \to \mathbf{R}](https://s0.wp.com/latex.php?latex=f%3A+%5B+a%2Cb%5D+%5Cto+%5Cmathbf%7BR%7D&bg=ffffff&fg=545454&s=0&c=20201002) of one real variable.
of one real variable.
Could you please motivate these terms? What does it mean to call one of them as signed and the other as unsigned?
24 April, 2022 at 7:04 am
N is a number
OK, I realize that the terms are adopted to distinguish between the cases of assigning or not assigning an orientation to the region or domain of integration.
Is this the only reason?
25 April, 2022 at 11:46 am
Terence Tao
The unsigned integral![\int_{[a,b]} f(x)\ dx](https://s0.wp.com/latex.php?latex=%5Cint_%7B%5Ba%2Cb%5D%7D+f%28x%29%5C+dx&bg=ffffff&fg=545454&s=0&c=20201002) of an unsigned function
of an unsigned function  is still unsigned, but the signed integral
is still unsigned, but the signed integral 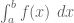 of an unsigned function can be negative if
of an unsigned function can be negative if  .
.
29 May, 2022 at 12:32 am
Aditya Guha Roy
Exercise 12 can be solved by noticing that finite arc length implies inite 1-dimensional Hausdorff measure, which yields zero 2-dimensional Hausdorff measure.
Is there a more elementary proof without considering Hausdorff measures?
29 May, 2022 at 3:52 am
Aditya Guha Roy
(Minor correction) In Line number 10 in the proof of Proposition 10 (Arc-length formula) there is a mismatch of and
and  when you write
when you write 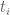 while indexing the summands by
while indexing the summands by  .
.
[Corrected, thanks – T.]
29 May, 2022 at 4:09 am
Aditya Guha Roy
Also none of the tricki links are in working condition anymore. It says that the “site is offline”.
7 June, 2022 at 4:28 am
Cheng Yui To
For exercise 14, the reparametrization will not be continuous if the curve is constant on some interval right?
[Oops, this hypothesis needs to be added, thanks – T.]