[This post should have appeared several months ago, but I didn’t have a link to the newsletter at the time, and I subsequently forgot about it until now. -T.]
Last year, Emmanuel Candés and I were two of the recipients of the 2008 IEEE Information Theory Society Paper Award, for our paper “Near-optimal signal recovery from random projections: universal encoding strategies?” published in IEEE Inf. Thy.. (The other recipient is David Donoho, for the closely related paper “Compressed sensing” in the same journal.) These papers helped initiate the modern subject of compressed sensing, which I have talked about earlier on this blog, although of course they also built upon a number of important precursor results in signal recovery, high-dimensional geometry, Fourier analysis, linear programming, and probability. As part of our response to this award, Emmanuel and I wrote a short piece commenting on these developments, entitled “Reflections on compressed sensing“, which appears in the Dec 2008 issue of the IEEE Information Theory newsletter. In it we place our results in the context of these precursor results, and also mention some of the many active directions (theoretical, numerical, and applied) that compressed sensing is now developing in.
What's new 
11 comments
Comments feed for this article
28 May, 2009 at 7:58 am
Igor Carron
Dear Terry,
Thanks to you and Emmanuel for the plug about the blog in the newsletter!
Igor.
http://nuit-blanche.blogspot.com
29 July, 2009 at 2:56 pm
weiyu
just one simple question from the paper “Near Optimal Signal Recovery from Random Projections:Universal Encoding Strategies?”
For the Fourier ensemble, in order for the R.I.P conditions to hold, can we get the sparsity level, namely the cardinality of the signal support, be linearly growing with the problem dimension N, if we allow the number of freuqnecy sample grow linearly with the problem dimension N? In the paper, we can have N/log(N) growth, can we get rid of this constraint?
Many thanks for the reply.
3 August, 2009 at 5:44 am
Terence Tao
In the Gaussian case, this can be achieved; see for instance my joint paper with Candes, Rudelson, and Vershynin at http://www.math.ucla.edu/~tao/preprints/FOCS05.pdf (though the observation probably predates the explicit introduction of the RIP concept).
11 July, 2011 at 1:05 pm
Anonymous
In reading the proof of the UUP for the Fourier matrix from the “Universal Encoding Strategy paper”, http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4016283
two questions:
1. In the definition of the set {J_0,…,J_1} (right above Eq. (7.48) in the IEEE version), should the N^2 in the definition be N^{-2}?
2. In the telescoping expansion below Eq. (7.48). Is the expansion written in the right way. In this expansion, f_{J_{0}} was subtracted twice. Was there a typo there?
Thank you very much for your reply, which will greatly help understanding of this paper.
14 July, 2011 at 9:11 am
Terence Tao
Yes, there should be a minus sign in both cases (N^2 should be N^{-2}, and the telescoping series should have its sign reversed.)
22 November, 2011 at 6:47 pm
Richard
Dear Terry,
In your paper “Decoding by Linear Programming” you wish to recover an input vector
from corrupted measurements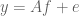 
. Can one change 
to be a square matrix? In other words, could you also ask given corrupted measurements can you recover an input matrix?
26 September, 2012 at 4:41 pm
Anonymous
Recently, I published a paper on the super robustness at:
http://arxiv.org/abs/1208.1810
Is there any insight on the relation between our approach and GGD used in compressive sensing? The main goal of our approach was to do pattern matching.
Any suggestions to extend the results to more general transformation than translation estimation?
27 September, 2012 at 7:28 pm
Anonymous
Sorry for the typo: “GGD used in compressive sensing” should read “GGD=based approaches used in compressive sensing”.
29 September, 2012 at 7:37 am
Anonymous
Mathematically, compressive sensing and super robustness of location estimation studied in http://arxiv.org/abs/1208.1810 are all related to a linear system A=BC. The difference is that in compressive sensing, A and B are all reliable but there are not enough equations to solve C, thus a “good guess” is generated using linear programming based on some kind of mathematics assumption; in the super robustness of location estimation, A and B contains a lot of noise or majority of the data in A and B are not reliable, the paper presents an approach how to generate a reliable C from the very noisy data.
6 September, 2013 at 11:05 am
Anonymous
The newsletter is missing from the website. Could Professor Tao help upload a direct link to the newsletter article here? Thanks.
26 September, 2013 at 3:47 pm
Igor Carron
Anonymous,
It is here: http://www-stat.stanford.edu/~candes/papers/itNL1208.pdf
Igor.