In the theory of discrete random matrices (e.g. matrices whose entries are random signs ), one often encounters the problem of understanding the distribution of the random variable
, where
is an
-dimensional random sign vector (so
is uniformly distributed in the discrete cube
), and
is some
-dimensional subspace of
for some
.
It is not hard to compute the second moment of this random variable. Indeed, if denotes the orthogonal projection matrix from
to the orthogonal complement
of
, then one observes that
and so upon taking expectations we see that
since is a rank
orthogonal projection. So we expect
to be about
on the average.
In fact, one has sharp concentration around this value, in the sense that with high probability. More precisely, we have
Proposition 1 (Large deviation inequality) For any
, one has
for some absolute constants
.
In fact the constants are very civilised; for large
one can basically take
and
, for instance. This type of concentration, particularly for subspaces
of moderately large codimension
, is fundamental to much of my work on random matrices with Van Vu, starting with our first paper (in which this proposition first appears). (For subspaces of small codimension (such as hyperplanes) one has to use other tools to get good results, such as inverse Littlewood-Offord theory or the Berry-Esséen central limit theorem, but that is another story.)
Proposition 1 is an easy consequence of the second moment computation and Talagrand’s inequality, which among other things provides a sharp concentration result for convex Lipschitz functions on the cube ; since
is indeed a convex Lipschitz function, this inequality can be applied immediately. The proof of Talagrand’s inequality is short and can be found in several textbooks (e.g. Alon and Spencer), but I thought I would reproduce the argument here (specialised to the convex case), mostly to force myself to learn the proof properly. Note the concentration of
obtained by Talagrand’s inequality is much stronger than what one would get from more elementary tools such as Azuma’s inequality or McDiarmid’s inequality, which would only give concentration of about
or so (which is in fact trivial, since the cube
has diameter
); the point is that Talagrand’s inequality is very effective at exploiting the convexity of the problem, as well as the Lipschitz nature of the function in all directions, whereas Azuma’s inequality can only easily take advantage of the Lipschitz nature of the function in coordinate directions. On the other hand, Azuma’s inequality works just as well if the
metric is replaced with the larger
metric, and one can conclude that the
distance between
and
concentrates around its median to a width
, which is a more non-trivial fact than the
concentration bound given by that inequality. (The computation of the median of the
distance is more complicated than for the
distance, though, and depends on the orientation of
.)
Remark 1 If one makes the coordinates of
iid Gaussian variables
rather than random signs, then Proposition 1 is much easier to prove; the probability distribution of a Gaussian vector is rotation-invariant, so one can rotate
to be, say,
, at which point
is clearly the sum of
independent squares of Gaussians (i.e. a chi-square distribution), and the claim follows from direct computation (or one can use the Chernoff inequality). The gaussian counterpart of Talagrand’s inequality is more classical, being essentially due to Lévy, and will also be discussed later in this post.
— 1. Concentration on the cube —
Proposition 1 follows easily from the following statement, that asserts that if a convex set occupies a non-trivial fraction of the cube
, then the neighbourhood
will occupy almost all of the cube for
:
Proposition 2 (Talagrand’s concentration inequality) Let
be a convex set in
. Then
for all
and some absolute constant
, where
is chosen uniformly from
.
Remark 2 It is crucial that
is convex here. If instead
is, say, the set of all points in
with fewer than

‘s, then
is comparable to
, but
only starts decaying once
, rather than
. Indeed, it is not hard to show that Proposition 2 implies the variant
for non-convex
(by restricting
to
and then passing from
to the convex hull, noting that distances to
on
may be contracted by a factor of
by this latter process); this inequality can also be easily deduced from Azuma’s inequality.
To apply this proposition to the situation at hand, observe that if is the cylindrical region
for some
, then
is convex and
is contained in
. Thus
Applying this with or
, where
is the median value of
, one soon obtains concentration around the median:
This is only compatible with (1) if , and the claim follows.
To prove Proposition 2, we use the exponential moment method. Indeed, it suffices by Markov’s inequality to show that
for a sufficiently small absolute constant (in fact one can take
).
We prove (2) by an induction on the dimension . The claim is trivial for
, so suppose
and the claim has already been proven for
.
Let us write for
. For each
, we introduce the slice
, then
is convex. We now try to bound the left-hand side of (2) in terms of
rather than
. Clearly
By symmetry we may assume that , thus we may write
where and
.
Now we look at . For
, let
be the closest point of (the closure of)
to
, thus
Let be chosen later; then the point
lies in
by convexity, and so
Squaring this and using Pythagoras, one obtains
As we will shortly be exponentiating the left-hand side, we need to linearise the right-hand side. Accordingly, we will exploit the convexity of the function to bound
and thus by (4)
We exponentiate this and take expectations in (holding
fixed for now) to get
Meanwhile, from the induction hypothesis and (3) we have
and similarly for . By Hölder’s inequality, we conclude
For , the optimal choice of
here is
, obtaining
for , the optimal choice of
is to be determined. Averaging, we obtain
so to establish (2), it suffices to pick such that
If is bounded away from zero, then by choosing
we would obtain the claim if
is small enough, so we may take
to be small. But then a Taylor expansion allows us to conclude if we take
to be a constant multiple of
, and again pick
to be small enough. The point is that
already almost works up to errors of
, and increasing
from zero to a small non-zero quantity will decrease the LHS by about
. [By optimising everything using first-year calculus, one eventually gets the constant
claimed earlier.]
Remark 3 Talagrand’s inequality is in fact far more general than this; it applies to arbitrary products of probability spaces, rather than just to
, and to non-convex
, but the notion of distance needed to define
becomes more complicated; the proof of the inequality, though, is essentially the same. Besides its applicability to convex Lipschitz functions, Talagrand’s inequality is also very useful for controlling combinatorial Lipschitz functions
which are “locally certifiable” in the sense that whenever
is larger than some threshold
, then there exist some bounded number
of coefficients of
which “certify” this fact (in the sense that
for any other
which agrees with
on these coefficients). See e.g. the text of Alon and Spencer for a more precise statement and some applications.
— 2. Gaussian concentration —
As mentioned earlier, there are analogous results when the uniform distribution on the cube are replaced by other distributions, such as the
-dimensional Gaussian distribution. In fact, in this case convexity is not needed:
Proposition 3 (Gaussian concentration inequality) Let
be a measurable set in
. Then
for all
and some absolute constant
, where
is a random Gaussian vector.
This inequality can be deduced from Lévy’s classical concentration of measure inequality for the sphere (with the optimal constant), but we will give an alternate proof due to Maurey and Pisier. It suffices to prove the following variant of Proposition 3:
Proposition 4 (Gaussian concentration inequality for Lipschitz functions) Let
be a function which is Lipschitz with constant
(i.e.
for all
. Then for any
we have
for all
and some absolute constant
, where
is a random variable. [Informally, Lipschitz functions of Gaussian variables concentrate as if they were Gaussian themselves; for comparison, Talagrand’s inequality implies that convex Lipschitz functions of Bernoulli variables concentrate as if they were Gaussian.]
Indeed, if one sets , and splits into the cases whether
or
, one obtains either
(in the former case) or
, and so
in either case. Also, since , we have
. Putting the two bounds together gives the claim.
Now we prove Proposition 4. By the epsilon regularisation argument we may take to be smooth, and so by the Lipschitz property we have
for all . By subtracting off the mean we may assume
. By replacing
with
if necessary it suffices to control the upper tail probability
for
.
We again use the exponential moment method. It suffices to show that
for some absolute constant .
Now we use a variant of the square and rearrange trick. Let be an independent copy of
. Since
, we see from Jensen’s inequality that
, and so
With an eye to exploiting (5), one might seek to use the fundamental theorem of calculus to write
But actually it turns out to be smarter to use a circular arc of integration, rather than a line segment:
The reason for this is that is another gaussian random variable equivalent to
, as is its derivative
; furthermore, and crucially, these two random variables are independent.
To exploit this, we first use Jensen’s inequality to bound
Applying the chain rule and taking expectations, we have
Let us condition to be fixed, then
; applying (5), we conclude that
is normally distributed with standard deviation at most
. As such we have
for some absolute constant ; integrating out the conditioning on
we obtain the claim.

41 comments
Comments feed for this article
9 June, 2009 at 8:39 pm
student
Dear Prof Tao,
How do you pass from line segment integral to circular arc integral?
by change of variable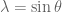 ?
?
thanks
9 June, 2009 at 9:28 pm
Terence Tao
Dear student,
The circular arc identity is established directly from the fundamental theorem of calculus , rather than from applying a change of variables from the line segment identity (which doesn’t work). The point is that in higher dimensions, there are many inequivalent ways to apply the fundamental theorem of calculus to expand f(Y)-f(X) – one for each path from X to Y, and the key is to select the right one.
, rather than from applying a change of variables from the line segment identity (which doesn’t work). The point is that in higher dimensions, there are many inequivalent ways to apply the fundamental theorem of calculus to expand f(Y)-f(X) – one for each path from X to Y, and the key is to select the right one.
15 June, 2009 at 10:35 pm
student
Dear Prof. Tao,
I remember once you wrote that you will teach random matrix theory next semester. my request is that
Would you please start to post little by little some notes related to prerequisite material for that course? if we start to study during summer and get enough background it would be perfect for us.
thank you very much
16 June, 2009 at 7:10 am
Terence Tao
Actually, the class will be starting in the winter quarter (next January). I have not yet decided exactly what the topics will be, but apart from a basic graduate education in analysis, probability, linear algebra, and combinatorics it should be fairly self-contained.
16 June, 2009 at 11:59 am
Oded
One minor comment: the statement in Remark 2 seems almost vacuous. After all, the distance between *any* two points in {-1,+1}^n is at most 2\sqrt{n}. Maybe the correct behavior should be n^{1/4}?
16 June, 2009 at 12:25 pm
Terence Tao
Hmm, good point. On the other hand, the Azuma/McDiarmid argument also works if the metric is replaced by the much larger
metric is replaced by the much larger 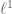 metric (although the mean or median of
metric (although the mean or median of  is somewhat harder to compute in that case). I’ll adjust the text to reflect this. (One could make the case that Talagrand’s inequality is to
is somewhat harder to compute in that case). I’ll adjust the text to reflect this. (One could make the case that Talagrand’s inequality is to  as Azuma’s inequality or McDiarmid’s inequality is to
as Azuma’s inequality or McDiarmid’s inequality is to 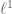 ; note the crucial use of Pythagoras’ theorem in the middle of the proof of Talagrand’s inequality.)
; note the crucial use of Pythagoras’ theorem in the middle of the proof of Talagrand’s inequality.)
16 June, 2009 at 8:58 pm
vedadi
Dear Prof. Tao,
just after ” square and rearrange trick”, you say that you use Jensen’s inequality.
I guess your convex function is for
for 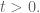
in that case why do not we have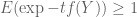 ?
?
Jensen’s ineq is , right?
, right?
thanks
16 June, 2009 at 9:16 pm
Terence Tao
Dear vedadi,
Yes, that was a typo, the expectation should be at least 1, rather than at most 1. (The subsequent inequalities did not have the typo, though.)
17 June, 2009 at 9:11 pm
student
Dear Prof Tao,
When we say ”let Y be an independent copy of X….” How do we guarantee the existence of that copy? Don’t we have some philosophical questions here too?
thanks
18 June, 2009 at 8:59 am
Terence Tao
Dear student,
Independent copies of a random variable can always be generated by the product measure construction,
http://en.wikipedia.org/wiki/Product_measure
This requires extending the underlying probability space to a finer one, but probability theory is designed in such a way that one can always do this without affecting any probabilistically meaningful quantities, such as probabilities of events or expectations, moments, correlations, and distributions of random variables. (As such, one of the guiding philosophies of probability theory is to not work with the underlying probability space if at all possible. The situation is somewhat analogous to differential geometry, which is designed to be invariant under changes of coordinates, and so the philosophy is often to avoid explicit manipulation of such coordinates whenever possible.)
Kallenberg’s “Foundations of modern probability” is a good reference for these sorts of foundational issues. However, it should be said that while such issues are of course important, especially from a philosophical or logical point of view, they rarely affect day-to-day usage of probability, much as the construction of the real numbers does not play a prominent role in real arithmetic, or as the construction of the Lebesgue integral does not play a prominent role in computation and estimation of integrals.
18 June, 2009 at 11:39 am
Anonymous
Dear Prof. Tao,
Could you please write a blog post on ”Large Deviation Principles” this summer by explaining the theory by examples and from your point of view?
thanks
2 July, 2009 at 6:05 am
ebrima saye
You are inspirational!!
2 July, 2009 at 7:57 pm
student
Dear Prof. Tao,
I could not find in which part I am doing a mistake in the following argument :
we know that if two random variables have the same distribution then their mean is the same. now
Let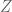 be a standard normal rv. and
be a standard normal rv. and 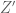 be an independent copy of it. then
be an independent copy of it. then  and
and  have the same distribution (?) but
have the same distribution (?) but ![E[Z \cdot Z]=1](https://s0.wp.com/latex.php?latex=E%5BZ+%5Ccdot+Z%5D%3D1&bg=ffffff&fg=545454&s=0&c=20201002) and
and ![E[Z \cdot Z^{\prime}]=E[Z]E[Z^{\prime}]=0](https://s0.wp.com/latex.php?latex=E%5BZ+%5Ccdot+Z%5E%7B%5Cprime%7D%5D%3DE%5BZ%5DE%5BZ%5E%7B%5Cprime%7D%5D%3D0&bg=ffffff&fg=545454&s=0&c=20201002)
what is going on here?
thanks
3 July, 2009 at 7:58 am
Terence Tao
Dear student:
The same issue crops up if Z is a Bernoulli distribution (equal to +1 with probability 1/2, and -1 with probability -1/2). This example is elementary enough that you can work out everything from first principles; if you do so, you should see the error.
Dear Ben: X decomposes into two orthogonal components, PX and X-PX. X-PX is the orthogonal projection of X to V, so the distance from X to V is the length of PX. Since P is an orthogonal projection,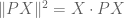 .
.
Alternatively, one can pick a coordinate system so that V is a coordinate plane, in which case all calculations can be done explicitly.
3 July, 2009 at 4:56 am
ben
Dear Prof Tao
could you explain why
thanks
5 July, 2009 at 3:33 pm
Anonymous
Dear Prof. Tao,
I did not see at which step you are using the independence of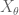 and
and 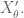
and in the last paragraf, when you say ” let’s condition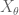 to be fixed….” do you mean you that you are using the following fact:
to be fixed….” do you mean you that you are using the following fact:
thanks
6 July, 2009 at 12:57 pm
Terence Tao
Yes, this is what is happening when one is conditioning on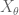 . The independence of
. The independence of 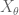 and
and 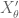 is used precisely at this step, to ensure that
is used precisely at this step, to ensure that 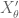 retains its normal distribution even after conditioning on a fixed value of
retains its normal distribution even after conditioning on a fixed value of 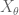 .
.
6 July, 2009 at 11:19 pm
lutfu
Dear Prof. Tao,
Let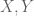 be two independent standart normal r.vs. then
be two independent standart normal r.vs. then
since![E[\exp(X \cdot Y) | Y=t]=\exp(t^2/2)](https://s0.wp.com/latex.php?latex=E%5B%5Cexp%28X+%5Ccdot+Y%29+%7C+Y%3Dt%5D%3D%5Cexp%28t%5E2%2F2%29&bg=ffffff&fg=545454&s=0&c=20201002) we have
we have
is this argument true?
in which step we are using independence of and
and 
thanks
7 July, 2009 at 6:33 am
Terence Tao
Yes, this is correct. The independence is needed to establish the identity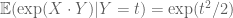 (because one needs X to remain normally distributed after conditioning on the event Y=t).
(because one needs X to remain normally distributed after conditioning on the event Y=t).
8 July, 2009 at 4:07 pm
lutfu
Dear Prof Tao,
Let be a seq of i.i.d. rvs. with mean zero.
be a seq of i.i.d. rvs. with mean zero.
as we know from as
as  the distribution of
the distribution of
Under the existence of second moment we know the limiting distribution of
my question is that do we know the distribution of
 for
for  under the suitable conditions? to which measure do they concentrate?
under the suitable conditions? to which measure do they concentrate?
thanks
8 July, 2009 at 7:57 pm
Anonymous
Dear Prof. Tao,
Could you please give a proof for the Azuma-Hoeffding inequality?
thanks
3 January, 2010 at 10:22 pm
254A, Notes 1: Concentration of measure « What’s new
[…] by induction on dimension . In the case when are Bernoulli variables, this can be done; see this previous blog post. In the general case, it turns out that in order to close the induction properly, one must […]
5 January, 2010 at 4:20 pm
254A, Notes 0: A review of probability theory « What’s new
[…] by induction on dimension . In the case when are Bernoulli variables, this can be done; see this previous blog post. In the general case, it turns out that in order to close the induction properly, one must […]
13 June, 2010 at 1:23 pm
Laurent Jacques
Dear Terence,
Thank you for this verrry interesting post. I’d like to share with you some elements.
From what I know, Sub-Gaussian Random Variable (SGRV), such as Bernoulli RV, centered Uniform RV, Gaussian RV, … are defined as follows:
X is a SGRV if there exists one c>0 such that for all real value s,
E[ \exp (s X) ] <= exp (c^2 s^2/2)
See for instance V. V. Buldygin publications, e.g. "Sub-Gaussian random variables", doi:10.1007/BF01087176
If I'm not wrong, one interesting property of SBRV is that any linear combination of SGRV is SGRV with known characteristics. In particular, the "Gaussian standard", defined as the minimal "c" such that the definition above holds, behaves as the standard deviation of Gaussian RV with respect to linear combination of SGRV.
This implies also that if you rotate a sub-Gaussian random vector with iid SGRV components, you get also a sub-Gaussian random vector. The components of this latter are perhaps not iid anymore but at least they have all the same "Gaussian standard".
My question is thus the following:
**Do you think that Theorem 4 above could be easily generalized to sub-Gaussian random vectors of components with unit gaussian standard?**
It seems indeed that in many places in you proof, you use already key ingredients for this generalization:
* the sub-gaussian inequality definition;
* linear combinations (rotation) of Gaussian RVs which are themselves Gaussian.
Or perhaps this generalization is already known in the community (I didn't see it anyway in Talagrand/Ledoux's books)?
Best,
Laurent
18 August, 2010 at 12:43 am
Anonymous
Dear Prof. Tao
I have two questions about the proof for Proposition 4.
Firstly, It seems that there is a typo when you bound
exp(t(F(X)-F(Y))) by using Jensen Inequality, please check it if possible.
Secondly, the aim is
Eexp(tF(X))<=exp(Ct^2),
but the proof only tells us
Eexp(tF(X))<=exp(Ct),
Please give some explaination if possible.
Thanks.
[Corrected, thanks – T.]
20 August, 2010 at 2:50 am
Anonymous
Dear Prof. Tao
Have you checked the bound of exp(t(F(X)-F(Y))) in the proof of Proposition 4? There is still a typo in my opinion.
[Corrected, thanks – T.]
21 August, 2010 at 2:16 am
Anonymous
Dear Prof. Tao ? Some hints will be OK.
? Some hints will be OK.
Can you tell me how to get
21 August, 2010 at 7:30 am
Terence Tao
If X is a Gaussian with mean zero and variance , then the moment generating function is
, then the moment generating function is  , as can be seen by completing the square.
, as can be seen by completing the square.
22 August, 2010 at 4:41 am
Anonymous
Dear Prof. Tao
I get it. Thanks for your reply. So far I have got a lot of interesting and useful mathemetical knowledge from your blog. Your earnest attitude and diligence impressed me. Thanks again.
16 November, 2010 at 10:04 pm
The Determinant of Random Bernoulli Matrices « Tsourolampis Blog
[…] [6] Talagrand’s inequality https://terrytao.wordpress.com/2009/06/09/talagrands-concentration-inequality/ […]
25 April, 2011 at 2:44 pm
Anonymous
Dear Prof. Tao,
is Talagrand concentration inequality still valid if we have independent but not identically distributed normally distributed component of ?
?
Thanks
8 May, 2012 at 1:15 am
Anonymous
Hi Professor Tao,
Does dist(X,V) = euclidean distance(X,V)?
Thanks.
[Yes – T.]
12 May, 2012 at 5:32 pm
sabyasachi chatterjee
Hello Professor Tao,
I have had to investigate the concentration of the log determinant of a matrix. Specifically, suppose M1,..Mk are random matrices p by p, iid from a given distribution(can assume that the entries of the matrix are bounded a.s or other regularity conds if needed) whose expected value is the identity matrix I. Now if I consider the matrix mean..(M1+…Mk)/k and look at its log determinant..will it concentrate around its mean? Will the mean go to zero as k go to infinity? Hence will it concentrate around 0? Is there any known result on this? Thanks
9 July, 2012 at 10:53 pm
mathepsilon
Does that mean, the small constant c in the gaussian concentration inequaltiy for lipschitz function is (pi^2)/8? Thank you! I really can not find this constant elsewhere.
10 July, 2012 at 9:08 am
Terence Tao
Well, the arguments given in the above post are not necessarily optimal; there may be other arguments that give a better value of c. (Note also that the value of c in Proposition 3 and Proposition 4 may differ, for instance the above arguments give a loss of a factor of 4 when passing from the latter to the former.)
I would try Ledoux’s book, as it has a number of proofs of this inequality and may discuss the question of optimal constants somewhere. (For instance, log-Sobolev methods tend to be quite sharp in general, and should yield good results in this case.)
17 December, 2013 at 2:11 pm
Anonymous
Dear Terry Tao,
can you get limit behavior of dist(X,V) (using Talagrand inequality or otherwise)?
Proposition 1 suggests that perhaps (after properly normalizing), the distribution of dist(X,V) converges to the normal distribution. Is it true?
I think it would nicely illustrate the strength of the presented method — similarly to the comparison of Chernoff bound and Central limit theorem.
Thanks,
Robert Samal
17 December, 2013 at 4:42 pm
Terence Tao
When X is a gaussian vector, then dist(X,V)^2 is a chi-squared distribution (with the number of degrees of freedom equal to the codimension of V), and so the central limit theorem shows that dist(X,V)^2 (and thus also dist(X,V)) is approximately gaussian when the codimension is large. For small codimension, one gets a chi distribution instead.
In the non-gaussian case, one can presumably get similar results either through a Lindeberg exchange argument, or through a central limit theorem for quadratic forms, although I don’t know if this has been done explicitly in the literature.
28 August, 2014 at 11:39 pm
Anonymous
Is proposition 4 valid for idd rvs with exponential moments?
12 September, 2015 at 2:46 pm
Anonymous
Small typo in props 3 and 4: n should be d (or vice versa)
[Corrected, thanks – T.]
15 December, 2018 at 4:53 pm
Ray
Dear Prof. Tao,
I am confused about some detail of the proof to proposition 2. How is defined when
defined when  is an open set? And how is (4) defined if
is an open set? And how is (4) defined if  are empty sets?
are empty sets?
Thanks!
15 December, 2018 at 8:41 pm
Ray
never mind, I realized that these details can be worked out and does not affect the proof.