I’ve just uploaded to the arXiv the paper A remark on partial sums involving the Möbius function, submitted to Bull. Aust. Math. Soc..
The Möbius function is defined to equal
when
is the product of
distinct primes, and equal to zero otherwise; it is closely connected to the distribution of the primes. In 1906, Landau observed that one could show using purely elementary means that the prime number theorem
(where denotes a quantity that goes to zero as
) was logically equivalent to the partial sum estimates
we give a sketch of the proof of these equivalences below the fold.
On the other hand, these three inequalities are all easy to prove if the terms are replaced by their
counterparts. For instance, by observing that the binomial coefficient
is bounded by
on the one hand (by Pascal’s triangle or the binomial theorem), and is divisible by every prime between
and
on the other hand, we conclude that
from which it is not difficult to show that
Also, since , we clearly have
Finally, one can also show that
Indeed, assuming without loss of generality that is a positive integer, and summing the inversion formula
over all
one sees that
and the claim follows by bounding by
.
In this paper I extend these observations to more general multiplicative subsemigroups of the natural numbers. More precisely, if is any set of primes (finite or infinite), I show that
where is the multiplicative semigroup generated by
, i.e. the set of natural numbers whose prime factors lie in
.
Actually the methods are completely elementary (the paper is just six pages long), and I can give the proof of (7) in full here. Again we may take to be a positive integer. Clearly we may assume that
as the claim is trivial otherwise.
If denotes the primes that are not in
, then Möbius inversion gives us
Summing this for gives
We can bound and so
The claim now follows from (9), since and
overlap only at
.
As special cases of (7) we see that
and
for all . Since
, we also have
One might hope that these inequalities (which gain a factor of over the trivial bound) might be useful when performing effective sieve theory, or effective estimates on various sums involving the primes or arithmetic functions.
This inequality (7) is so simple to state and prove that I must think that it was known to, say, Landau or Chebyshev, but I can’t find any reference to it in the literature. [Update, Sep 4: I have learned that similar results have been obtained in a paper by Granville and Soundararajan, and have updated the paper appropriately.] The proof of (8) is a simple variant of that used to prove (7) but I will not detail it here.
Curiously, this is one place in number theory where the elementary methods seem superior to the analytic ones; there is a zeta function associated to this problem, but it need not have a meromorphic continuation beyond the region
, and it turns out to be remarkably difficult to use this function to establish the above results. (I do have a proof of this form, which I in fact found before I stumbled on the elementary proof, but it is far longer and messier.)
— 1. Equivalences —
We now show the equivalences between (1), (2), and (3). The arguments here are drawn from this article of Diamond; I will skip some of the details in order to focus on the main ideas.
It is convenient to introduce the von Mangoldt function , defined as
when
is a prime
(or a power of that prime), and zero otherwise. It is not difficult to see that the prime number theorem (1) is equivalent to the asymptotic
Now we show that (10) implies (2). The starting point is the identity
connecting and
, which is the coefficient form of the identity
involving the Riemann zeta function . Summing this identity for
, one obtains the formula
Using the Chebyshev bound (4), one can bound by
; using (10), one can refine this to
for any
when
is large enough. Using these bounds together with (5), one can show that the right-hand side of (11) is
. It is not too difficult to get to (2) from here (e.g. by summation by parts).
To get from (2) to (3), we use (6). A summation by parts argument using (2) shows that
for any fixed (basically because the function
has bounded variation). Letting
go to infinity and using (6) we obtain (3). Conversely, a summation by parts argument easily deduces (2) from (3).
Finally, to get back from (2) and (3) to (10), we use the identities
where is the divisor function; these identities are the coefficient forms of the identities
and
Expanding out using these formulae, we see that to prove (10) it suffices to show that
From the Dirichlet hyperbola method one can show that
for some absolute constant (in fact
, where
is Euler’s constant), and from Stirling’s formula one has
and so
From this, (2), (3), and summation by parts one soon obtains (14).
Remark 1 These equivalences are elementary, but somewhat ad hoc in nature. A less elementary, but more “natural”, approach would be to rewrite everything in terms of the Riemann zeta function, and in particular to show that (10), (2), (3) are all equivalent to the assertion that the zeta function has a simple pole at
and no other poles or zeroes on the line
. This approach can of course be found in any introductory analytic number theory text.

29 comments
Comments feed for this article
30 August, 2009 at 9:21 pm
Anonymous
Terry:
Should this be tagged as ‘paper’ instead of ‘expository’? [Corrected, thanks. -T]
31 August, 2009 at 8:46 am
Anonymous
Dear Prof. Tao,
The spelling of Hans von Mangoldt’s name seems to be incorrect, in the second paragraph of section 1. (Feel free to delete this nitpicky post, also!) [Corrected, thanks – T.]
31 August, 2009 at 9:24 am
Anonymous
Dear Terry,
The arxiv link to the paper doesn’t seem to be the right one. [Oops, the paper hasn’t appeared on the arXiv yet. It should within a day or so. -T]
31 August, 2009 at 11:03 am
Anonymous
I don’t see how you get the number 1 on the far left of equation (6). Should that be x instead? (in which case you would get 2, not 1, as the desired bound).
31 August, 2009 at 12:43 pm
Terence Tao
The sum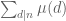 equals 1 for n=1 and zero otherwise, so
equals 1 for n=1 and zero otherwise, so 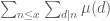 is equal to 1 for
is equal to 1 for 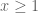 . This sum can then be rearranged as
. This sum can then be rearranged as 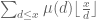 .
.
31 August, 2009 at 9:28 pm
Anonymous
Thanks!
1 September, 2009 at 1:06 am
Andrew V. Sutherland
Below is a simple example that I believe proves your conjecture that the sum
S(G,x) = sum_{n \ in G : n <= x} mu(n)/n
diverges for certain mutliplicative subsemigroups G of the natural numbers.
Let P be the set of positive integers n=pq that are the product of two primes, and let G=. For an element n of G, we have mu(n)=1 when n is square-free and mu(n) = 0 otherwise. In particular, mu(n) >= 0 for all n \in G, hence if S(G,x) converges, it does so absolutely.
But note that S(G,x) is bounded below by 1/2 sum_{2<p<=x} 1/p, which diverges, by Mertens' second theorem (sum_{p<=x} 1/p ~ loglog(x)).
1 September, 2009 at 1:09 am
Andrew V. Sutherland
Here G = \langle P \rangle is the semigroup generated by P.
1 September, 2009 at 1:32 am
Terence Tao
Ah, yes, that seems to work, thanks!
2 September, 2009 at 11:23 am
Kevin O'Bryant
If you search for “Beurling numbers” on Google (or Math SciNet, I suppose, although I don’t have access at the moment), you’ll find many related articles. Harold Diamond at the University of Illinois is an expert.
If I recall correctly, Beurling numbers are defined in the following manner. Let {p_1<p_2 < …} be an increasing sequence of real numbers, all larger than 1. These are our "Beurling primes". The "Beurling numbers" are the semigroup generated by the p_i, counting mulitiplicity. The general idea is that if the Beurling numbers are enough like the positive integers, then the Beurling primes are very similar to the primes. For example, there's a theorem along the lines of "If the number of Beurling numbers less than x is asymptotically cx (for any positive constant c, with a nice error term), then the number of Beurling primes less than x is asymptotically x/log(x)." In other words, the prime number theorem isn't really about the integers, it's just talking about semigroups of reals with linear growth.
Interestingly, the PNT error term can provably not be improved in this setting. It seems that any progress on the error term, the Riemann Hypothesis included, *must* utilize some properties of the integers aside from their multiplicative structure.
I learned about this line from a grad student at Illinois (Italian, but I don't recall his name) whose thesis was showing that for almost all (in some sense) choices of p_i, the Riemann Hypothesis does hold for the consequent zeta function.
I just found http://www.math.kth.se/~rikardo/beurling.pdf, which seems relevant.
2 September, 2009 at 12:39 pm
Anonymous
O’Bryant post is very interesting. However, in your next to last paragraph, do you mean “the Riemann Hypothesis doesn’t hold”? I would very much want to see the paper if you really mean otherwise.
6 September, 2009 at 8:40 pm
Kevin O'Bryant
Unfortunately, I don’t have any references. What I’ve heard has been in casual conversation and at seminars. The Italian student I referred to above is Eugene Balanzario, but I didn’t find any telling links with his name.
My impression is that the Riemann Hypothesis tends to hold (if the counting function for the Beurling numbers is ‘enough’ linear) in some rigorous sense, but that there are Beurling numbers with very linear growth where it fails. But, this is now third-hand info, that may not have been refereed to begin with. Harold Diamond is the one who should weigh in with the truth of things, what’s known true and known false.
15 September, 2009 at 1:34 pm
Eugenio P. Balanzario
Kevin, my second given name is Pacelli, which is certainly Italian, but I am not. You can easily produce examples of Beurling numbers for which the Riemann Hypothesis is either true or false. In my PhD thesis, written under the direction of Prof. Diamond, I considered the Mobius function of a particular set of Beurling numbers. This example is interesting because it shows that the prime number theorem is not equivalent (in the general setting of Beurling) to the statement M(x)=o(x) where M(x) is the sum of the Moubius function.
24 September, 2009 at 3:17 pm
The prime number theorem in arithmetic progressions, and dueling conspiracies « What’s new
[…] noted in this previous post, we […]
23 July, 2011 at 7:41 pm
Erdos’ divisor bound « What’s new
[…] This type of argument is also known as the Dirichlet hyperbola method. A variant of this argument can also deduce the prime number theorem from (3), (4) (and with some additional effort, one can even drop the use of (4)); this is discussed at this previous blog post. […]
14 October, 2012 at 5:43 pm
The Chowla conjecture and the Sarnak conjecture « What’s new
[…] already equivalent to the prime number theorem, as observed by Landau (see e.g. this previous blog post for a proof), while the much stronger (and still open) […]
27 July, 2014 at 8:33 am
089l8
I do not know whether there is such a hypothesis or theorem
 .
.
 .
.
I suppose it would be
27 July, 2014 at 11:39 am
089l8
Drew attention to the Dirichlet series is possible using them can be proved
17 August, 2016 at 1:21 am
Anonymous
Is it possible to estimate the number of negative values of sums of type (7) on some interval? Thanks.
17 August, 2016 at 3:14 am
Anonymous
Is it possible to extend the above results by requiring that the elements of the set (instead of being primes) are needed only to be “pseudo primes” in the sense of being in
(instead of being primes) are needed only to be “pseudo primes” in the sense of being in 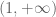 , having no accumulation points, and their logarithms independent over the rationals ?
, having no accumulation points, and their logarithms independent over the rationals ?
20 October, 2017 at 10:44 am
The logarithmically averaged and non-logarithmically averaged Chowla conjectures | What's new
[…] , this conjecture is equivalent to the prime number theorem (as discussed in this previous blog post), but the conjecture remains open for any […]
25 October, 2017 at 4:34 am
PLG
I am working on the combinatorics of walks on graphs, which is actually nothing more than a semi-commutative extension of number theory. Whist the tools provided by this approach are crude from the point of view of number theory (because they must function without knowledge of which primes do or do not commute), they seem to suggest that the average orders relation:
holds for all prime. While I cannot see how this is consistent with the result of Granville and Soundararajan, I am interested in understanding the relation between their result and the above, especially since the above, if indeed correct, can be obtained from essentially outside of number theory, in fact in a way that would work even in the absence or partial absence of commutativity between the primes. In the general case, the above result can be given a determinantal form valid on all graphs, and where the primes are the self-avoiding walks and polygons of the graph. Would anybody have an idea of the relation between this average order and the relaiton by Granville and Soundararajan?
prime. While I cannot see how this is consistent with the result of Granville and Soundararajan, I am interested in understanding the relation between their result and the above, especially since the above, if indeed correct, can be obtained from essentially outside of number theory, in fact in a way that would work even in the absence or partial absence of commutativity between the primes. In the general case, the above result can be given a determinantal form valid on all graphs, and where the primes are the self-avoiding walks and polygons of the graph. Would anybody have an idea of the relation between this average order and the relaiton by Granville and Soundararajan?
26 October, 2017 at 7:59 pm
Terence Tao
I don’t see any reason to expect this asymptotic; Perron’s formula suggests that the left-hand side should contain terms proportional to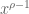 for every zero of the zeta function; one would only obtain a term of the form
for every zero of the zeta function; one would only obtain a term of the form  if
if 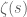 had a zero at
had a zero at 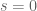 , which is not the case, and in any event it would be swamped by the zeroes in the critical strip (in particular, the LHS should only decay like
, which is not the case, and in any event it would be swamped by the zeroes in the critical strip (in particular, the LHS should only decay like 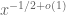 assuming standard conjectures such as RH). Some quick and dirty numerics (see https://terrytao.files.wordpress.com/2017/10/plot.png ) of the ratio of the LHS and RHS for
assuming standard conjectures such as RH). Some quick and dirty numerics (see https://terrytao.files.wordpress.com/2017/10/plot.png ) of the ratio of the LHS and RHS for 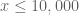 do not seem to indicate to me that the asymptotic holds. Perhaps there is a typo in the proposed asymptotic?
do not seem to indicate to me that the asymptotic holds. Perhaps there is a typo in the proposed asymptotic?
27 October, 2017 at 12:27 am
PLG
The result is supposed to be a statement on average orders, with clear fluctuations expected around. I did numerics as well up to 1000000 with various primes and the result holds pretty well. That said, I forgot a factor of 2 in the equation I wrote, which should read , where the
, where the  indicates only truth for the average order.
indicates only truth for the average order.
27 October, 2017 at 12:36 am
PLG
We are not plotting the same thing at all it seems, holds very well for various primes up to x>100000.
holds very well for various primes up to x>100000.
27 October, 2017 at 7:20 am
Terence Tao
Ah, I see what is going on now. The Dirichlet series of is
is  , which has a pole at every zero
, which has a pole at every zero 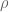 of
of  , but additionally has a further zero at
, but additionally has a further zero at 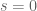 . Perron’s formula and the residue theorem indicates that each zero should contribute a term of the form
. Perron’s formula and the residue theorem indicates that each zero should contribute a term of the form  if I have calculated correctly, whereas the
if I have calculated correctly, whereas the 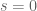 term should contribute
term should contribute 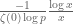 which is indeed
which is indeed  . This term is lower order than the contribution of the zeroes within the strip so one would not expect to see it in a pointwise sense even on RH, but one could in principle detect it if one averaged in a smooth enough fashion to damp out the effect of the zeroes. (Incidentally my plot previously was for
. This term is lower order than the contribution of the zeroes within the strip so one would not expect to see it in a pointwise sense even on RH, but one could in principle detect it if one averaged in a smooth enough fashion to damp out the effect of the zeroes. (Incidentally my plot previously was for 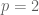 , and I suppose one could say that it was broadly consistent with the ratio eventually oscillating around 2.)
, and I suppose one could say that it was broadly consistent with the ratio eventually oscillating around 2.)
The results in Granville and Soundararajan contain error terms such as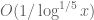 that are far larger than any of the orders of magnitude considered here, so there is no conflict between these claims and those in GS.
that are far larger than any of the orders of magnitude considered here, so there is no conflict between these claims and those in GS.
28 October, 2017 at 3:40 am
PLG
While the result itself is not so interesting, the fact that it holds is actually significant because it was derived from outside of number theory in a fashion that is valid and applicable on all graphs and furthermore because we have an infinite series of correction terms all of which we know perfectly well. I did a calculation to check the first correction term, and found the average order of Granville and Soundararajan second term (the one with 1- in front) etc. The third term is still unknown to number theory but accessible easy from graphs (I used the formalism layed out in our article on algebraic combinatorics in trace monoids), where this third term involves the second derivtive of a determinant, which will give rise to averages of functions of the type
in front) etc. The third term is still unknown to number theory but accessible easy from graphs (I used the formalism layed out in our article on algebraic combinatorics in trace monoids), where this third term involves the second derivtive of a determinant, which will give rise to averages of functions of the type  etc. There is an antire reservoir of advanced results here to be translated in number theory.
etc. There is an antire reservoir of advanced results here to be translated in number theory.
18 February, 2021 at 9:08 am
Daniel Seco
Thanks for this article! Is there any subsequence of the natural numbers for which we know the value or at least the sign of the l.h.s. of (3)?
14 March, 2021 at 12:50 pm
Bound on a scaled sum of the Liouville function ~ MathOverflow ~ mathubs.com
[…] Tao has shown see his blog post […]