This is yet another post in a series on basic ingredients in the structural theory of locally compact groups, which is closely related to Hilbert’s fifth problem.
In order to understand the structure of a topological group , a basic strategy is to try to split
into two smaller factor groups
by exhibiting a short exact sequence
If one has such a sequence, then is an extension of
by
(which includes direct products
and semidirect products
as examples, but can be more general than these situations, as discussed in this previous blog post). In principle, the problem of understanding the structure of
then splits into three simpler problems:
- (Horizontal structure) Understanding the structure of the “horizontal” group
.
- (Vertical structure) Understanding the structure of the “vertical” group
.
- (Cohomology) Understanding the ways in which one can extend
by
.
The “cohomological” aspect to this program can be nontrivial. However, in principle at least, this strategy reduces the study of the large group to the study of the smaller groups
. (This type of splitting strategy is not restricted to topological groups, but can also be adapted to many other categories, particularly those of groups or group-like objects.) Typically, splitting alone does not fully kill off a structural classification problem, but it can reduce matters to studying those objects which are somehow “simple” or “irreducible”. For instance, this strategy can often be used to reduce questions about arbitrary finite groups to finite simple groups.
A simple example of splitting is as follows. Given any topological group , one can form the connected component
of the identity – the maximal connected set containing the identity. It is not difficult to show that
is a closed (and thus also locally compact) normal subgroup of
, whose quotient
is another locally compact group. Furthermore, due to the maximal connected nature of
,
is totally disconnected – the only connected sets are the singletons. In particular,
is Hausdorff (the identity element is closed). Thus we have obtained a splitting
of an arbitrary locally compact group into a connected locally compact group , and a totally disconnected locally compact group
. In principle at least, the study of locally compact groups thus splits into the study of connected locally compact groups, and the study of totally disconnected locally compact groups (though the cohomological issues are not always trivial).
In the structural theory of totally disconnected locally compact groups, the first basic theorem in the subject is van Dantzig’s theorem (which we prove below the fold):
Theorem 1 (Van Danztig’s theorem) Every totally disconnected locally compact group
contains a compact open subgroup
(which will of course still be totally disconnected).
Example 1 Let
be a prime. Then the
-adic field
(with the usual
-adic valuation) is totally disconnected locally compact, and the
-adic integers
are a compact open subgroup.
Of course, this situation is the polar opposite of what occurs in the connected case, in which the only open subgroup is the whole group.
In view of van Dantzig’s theorem, we see that the “local” behaviour of totally disconnected locally compact groups can be modeled by the compact totally disconnected groups, which are better understood (for instance, one can start analysing them using the Peter-Weyl theorem, as discussed in this previous post). The global behaviour however remains more complicated, in part because the compact open subgroup given by van Dantzig’s theorem need not be normal, and so does not necessarily induce a splitting of into compact and discrete factors.
Example 2 Let
be a prime, and let
be the semi-direct product
, where the integers
act on
by the map
, and we give
the product of the discrete topology of
and the
-adic topology on
. One easily verifies that
is a totally disconnected locally compact group. It certainly has compact open subgroups, such as
. However, it is easy to show that
has no non-trivial compact normal subgroups (the problem is that the conjugation action of
on
has all non-trivial orbits unbounded).
Returning to more general locally compact groups, we obtain an immediate corollary:
Corollary 2 Every locally compact group
contains an open subgroup
which is “compact-by-connected” in the sense that
is compact.
Indeed, one applies van Dantzig’s theorem to the totally disconnected group , and then pulls back the resulting compact open subgroup.
Now we mention another application of van Dantzig’s theorem, of more direct relevance to Hilbert’s fifth problem. Define a generalised Lie group to be a topological group with the property that given any open neighbourhood
of the identity, there exists an open subgroup
of
and a compact normal subgroup
of
in
such that
is isomorphic to a Lie group. It is easy to see that such groups are locally compact. The deep Gleason-Yamabe theorem, which among other things establishes a satisfactory solution to Hilbert’s fifth problem (and which we will not prove here), asserts the converse:
Theorem 3 (Gleason-Yamabe theorem) Every locally compact group is a generalised Lie group.
Example 3 We consider the locally compact group
from Example 2. This is of course not a Lie group. However, any open neighbourhood
of the identity in
will contain the compact subgroup
for some integer
. The open subgroup
then has
isomorphic to the discrete finite group
, which is certainly a Lie group. Thus
is a generalised Lie group.
One important example of generalised Lie groups are those locally compact groups which are an inverse limit (or projective limit) of Lie groups. Indeed, suppose we have a family of Lie groups
indexed by partially ordered set
which is directed in the sense that every finite subset of
has an upper bound, together with continuous homomorphisms
for all
which form a category in the sense that
for all
. Then we can form the inverse limit
which is the subgroup of consisting of all tuples
which are compatible with the
in the sense that
for all
. If we endow
with the product topology, then
is a closed subgroup of
, and thus has the structure of a topological group, with continuous homomorphisms
which are compatible with the
in the sense that
for all
. Such an inverse limit need not be locally compact; for instance, the inverse limit
of Euclidean spaces with the usual coordinate projection maps is isomorphic to the infinite product space with the product topology, which is not locally compact. However, if an inverse limit
of Lie groups is locally compact, it can be easily seen to be a generalised Lie group. Indeed, by local compactness, any open neighbourhood of the identity will contain an open precompact neighbourhood of the identity; by construction of the product topology (and the directed nature of
), this smaller neighbourhood will in turn will contain the kernel of one of the
, which will be compact since the preceding neighbourhood was precompact. Quotienting out by this
we obtain a locally compact subgroup of the Lie group
, which is necessarily again a Lie group by Cartan’s theorem, and the claim follows.
In the converse direction, it is possible to use Corollary 2 to obtain the following observation of Gleason:
Theorem 4 Every Hausdorff generalised Lie group contains an open subgroup that is an inverse limit of Lie groups.
We show Theorem 4 below the fold. Combining this with the (substantially more difficult) Gleason-Yamabe theorem, we obtain quite a satisfactory description of the local structure of locally compact groups. (The situation is particularly simple for connected groups, which have no non-trivial open subgroups; we then conclude that every connected locally compact Hausdorff group is the inverse limit of Lie groups.)
Example 4 The locally compact group
is not an inverse limit of Lie groups because (as noted earlier) it has no non-trivial compact normal subgroups, which would contradict the preceding analysis that showed that all locally compact inverse limits of Lie groups were generalised Lie groups. On the other hand,
contains the open subgroup
, which is the inverse limit of the discrete (and thus Lie) groups
for
(where we give
the usual ordering, and use the obvious projection maps).
— 1. van Dantzig’s theorem —
To prove van Dantzig’s theorem, we first need a lemma from point set topology, which shows that totally disconnected spaces contain enough clopen sets to separate points:
Lemma 5 Let
be a totally disconnected compact Hausdorff space, and let
be distinct points in
. Then there exists a clopen set that contains
but not
.
Proof: Let be the intersection of all the clopen sets that contain
(note that
is obviously clopen). Clearly
is closed and contains
. Our objective is to show that
consists solely of
. As
is totally disconnected, it will suffice to show that
is connected.
Suppose this is not the case, then we can split where
are disjoint non-empty closed sets; without loss of generality, we may assume that
lies in
. As all compact Hausdorff spaces are normal, we can thus enclose
in disjoint open subsets
of
. In particular, the topological boundary
is compact and lies outside of
. By definition of
, we thus see that for every
, we can find a clopen neighbourhood of
that avoids
; by compactness of
(and the fact that finite intersections of clopen sets are clopen), we can thus find a clopen neighbourhood
of
that is disjoint from
. One then verifies that
is a clopen neighbourhood of
that is disjoint from
, contradicting the definition of
, and the claim follows.
Now we can prove van Dantzig’s theorem. We will use an argument from the book of Hewitt and Ross. Let be totally disconnected locally compact (and thus Hausdorff). Then we can find a compact neighbourhood
of the identity. By Lemma 5, for every
, we can find a clopen neighbourhood of the identity that avoids
; by compactness of
, we may thus find a clopen neighbourhood of the identity that avoids
. By intersecting this neighbourhood with
, we may thus find a compact clopen neighbourhood
of the identity. As
is both compact and open, we may then the continuity of the group operations find a symmetric neighbourhood
of the identity such that
. In particular, if we let
be the group generated by
, then
is an open subgroup of
contained in
and is thus compact as required.
Remark 1 The same argument shows that totally disconnected locally compact group contains arbitrarily small compact open subgroups, or in other words the compact open subgroups form a neighbourhood base for the identity.
— 2. Inverse limits —
Now we prove Theorem 4. Let be a Hausdorff generalised Lie group. By Corollary 2, we may find an open subgroup
such that
is compact. An easy application of Cartan’s theorem shows that
remains a Hausdorff generalised Lie group; we will show that it is in fact an inverse limit of Lie groups. The key fact is
Lemma 6 Let
be any open neighbourhood of the identity in
. Then there exists a compact normal subgroup
of
in
such that
is isomorphic to a Lie group.
Proof: Since is a generalised Lie group, we can find an open subgroup
of
and a compact normal subgroup
of
in
such that
is isomorphic to a Lie group.
As is an open group, it must be clopen, and in particular contains
. We conclude that
is an open subgroup of the compact group
, and is therefore finite index. In particular,
has only finitely many conjugates in
; intersecting them together, we obtain an open normal subgroup of
inside
, which pulls back to an open finite index normal subgroup
of
of inside
.
Let , then
is a compact normal subgroup of
.
is a locally compact subgroup of
; since
is isomorphic to a Lie group,
is also, by Cartan’s theorem. On the other hand, as
is an open normal subgroup,
is a discrete group. Using the short exact sequence
and noting that all outer automorphisms on a Lie group are smooth (as remarked on in the previous post), we conclude that is also isomorphic to a Lie group. The claim follows.
We can now let be the partially ordered set of compact normal subgroups of
, with the ordering of reverse inclusion (
if
); this is clearly a directed set. This gives a family of Lie groups
with the obvious projection maps
. By Lemma 6 and the Hausdorff property, the compact normal subgroups of
have trivial intersection, which shows that as a group,
is identifiable with the inverse limit
From Lemma 6 again we see that this identification is also a homeomorphism, and the claim follows.

11 comments
Comments feed for this article
30 May, 2011 at 10:05 pm
Anonymous
Missing expository tag. [Added, thanks – T.]
3 June, 2011 at 12:02 am
Florian
A couple of typos:
N should be normal (def. of generalised Lie group).
The link to “directed” is broken.
“Indeed, local compactness, any” is missing “by” probably?
[Corrected, thanks -T.]
12 June, 2011 at 9:25 am
Seventh Linkfest
[…] The Cotlar-Stein Lemma, Locally compact groups with faithful finite-dimensional representations, van Dantzig’s Theorem, The Furstenberg multiple recurrence theorem and finite […]
13 June, 2011 at 12:07 pm
Brouwer’s fixed point and invariance of domain theorems, and Hilbert’s fifth problem « What’s new
[…] There are results closely related to Theorem 4, such as the Gleason-Yamabe theorem mentioned in a recent post, which do not use the notion of being locally Euclidean, and do not require algebraic topological […]
13 June, 2011 at 6:31 pm
Laplace算子与表示论 « Fight with Infinity
[…] Tao van Dantzig’s theorem […]
30 June, 2011 at 11:38 pm
parça kontor
The global behaviour however remains more complicated
20 July, 2011 at 12:06 pm
Jesse Peterson
In Lemma 5 you say that all totally disconnected spaces are Hausdorff, but I don’t think this is quite correct. [Ah, right, they’re only T1 in general, though they are Hausdorff in the group case. In any case, I’ve corrected the article, thanks, -T.]
13 August, 2011 at 7:52 pm
The Hilbert-Smith conjecture « What’s new
[…] structural theory of locally compact groups (specifically, the Gleason-Yamabe theorem discussed in previous posts) and some results of Newman that sharply restrict the ability of periodic actions on a […]
29 November, 2012 at 3:14 pm
benbrawn
Example 3: ” G/N isomorphic to the discrete finite group …”
I think this should be G’/N based on the definition of generalised Lie group given above the example.
Great Blog BTW!
[Corrected, thanks – T.]
19 October, 2017 at 7:52 am
MahbubAlam231
In the proof of van Dantzig theorem, the clopen set that is disjoint from the {\partial K}, isn’t that clopen in {K} (I mean if you use Lemma 5)? How to make that clopen in {G}?
20 October, 2017 at 10:54 am
Terence Tao
A set which is closed in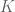 is automatically also closed in
is automatically also closed in  ; and a set which is open in
; and a set which is open in 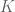 and avoids the boundary of
and avoids the boundary of 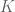 is automatically open in
is automatically open in  .
.