Our study of random matrices, to date, has focused on somewhat general ensembles, such as iid random matrices or Wigner random matrices, in which the distribution of the individual entries of the matrices was essentially arbitrary (as long as certain moments, such as the mean and variance, were normalised). In these notes, we now focus on two much more special, and much more symmetric, ensembles:
- The Gaussian Unitary Ensemble (GUE), which is an ensemble of random
Hermitian matrices
in which the upper-triangular entries are iid with distribution
, and the diagonal entries are iid with distribution
, and independent of the upper-triangular ones; and
- The Gaussian random matrix ensemble, which is an ensemble of random
(non-Hermitian) matrices
whose entries are iid with distribution
.
The symmetric nature of these ensembles will allow us to compute the spectral distribution by exact algebraic means, revealing a surprising connection with orthogonal polynomials and with determinantal processes. This will, for instance, recover the semi-circular law for GUE, but will also reveal fine spacing information, such as the distribution of the gap between adjacent eigenvalues, which is largely out of reach of tools such as the Stieltjes transform method and the moment method (although the moment method, with some effort, is able to control the extreme edges of the spectrum).
Similarly, we will see for the first time the circular law for eigenvalues of non-Hermitian matrices.
There are a number of other highly symmetric ensembles which can also be treated by the same methods, most notably the Gaussian Orthogonal Ensemble (GOE) and the Gaussian Symplectic Ensemble (GSE). However, for simplicity we shall focus just on the above two ensembles. For a systematic treatment of these ensembles, see the text by Deift.
— 1. The spectrum of GUE —
We have already shown using Dyson Brownian motion in Notes 3b that we have the Ginibre formula
for the density function of the eigenvalues of a GUE matrix
, where
is the Vandermonde determinant. We now give an alternate proof of this result (omitting the exact value of the normalising constant ) that exploits unitary invariance and the change of variables formula (the latter of which we shall do from first principles). The one thing to be careful about is that one has to somehow quotient out by the invariances of the problem before being able to apply the change of variables formula.
One approach here would be to artificially “fix a gauge” and work on some slice of the parameter space which is “transverse” to all the symmetries. With such an approach, one can use the classical change of variables formula. While this can certainly be done, we shall adopt a more “gauge-invariant” approach and carry the various invariances with us throughout the computation. (For a comparison of the two approaches, see this previous blog post.)
We turn to the details. Let be the space of Hermitian
matrices, then the distribution
of a GUE matrix
is a absolutely continuous probability measure on
, which can be written using the definition of GUE as
where is Lebesgue measure on
,
are the coordinates of
, and
is a normalisation constant (the exact value of which depends on how one normalises Lebesgue measure on
). We can express this more compactly as
Expressed this way, it is clear that the GUE ensemble is invariant under conjugations by any unitary matrix.
Let be the diagonal matrix whose entries
are the eigenvalues of
in descending order. Then we have
for some unitary matrix
. The matirx
is not uniquely determined; if
is diagonal unitary matrix, then
commutes with
, and so one can freely replace
with
. On the other hand, if the eigenvalues of
are simple, then the diagonal matrices are the only matrices that commute with
, and so this freedom to right-multiply
by diagonal unitaries is the only failure of uniqueness here. And in any case, from the unitary invariance of GUE, we see that even after conditioning on
, we may assume without loss of generality that
is drawn from the invariant Haar measure on
. In particular,
and
can be taken to be independent.
Fix a diagonal matrix for some
, let
be extremely small, and let us compute the probability
that lies within
of
in the Frobenius norm. On the one hand, the probability density of
is proportional to
near (where we write
) and the volume of a ball of radius
in the
-dimensional space
is proportional to
, so (2) is equal to
for some constant depending only on
, where
goes to zero as
(keeping
and
fixed). On the other hand, if
, then by the Weyl inequality (or Hoffman-Weilandt inequality) we have
(we allow implied constants here to depend on
and on
). This implies
, thus
. As a consequence we see that the off-diagonal elements of
are of size
. We can thus use the inverse function theorem in this local region of parameter space and make the ansatz
where is a bounded diagonal matrix,
is a diagonal unitary matrix, and
is a bounded skew-adjoint matrix with zero diagonal. (Note here the emergence of the freedom to right-multiply
by diagonal unitaries.) Note that the map
has a non-degenerate Jacobian, so the inverse function theorem applies to uniquely specify
(and thus
) from
in this local region of parameter space.
Conversely, if take the above form, then we can Taylor expand and conclude that
and so
We can thus bound (2) from above and below by expressions of the form
As is distributed using Haar measure on
,
is (locally) distributed using
times a constant multiple of Lebesgue measure on the space
of skew-adjoint matrices with zero diagonal, which has dimension
. Meanwhile,
is distributed using
times Lebesgue measure on the space of diagonal elements. Thus we can rewrite (4) as
where and
denote Lebesgue measure and
depends only on
.
Observe that the map dilates the (complex-valued)
entry of
by
, and so the Jacobian of this map is
. Applying the change of variables, we can express the above as
The integral here is of the form for some other constant
. Comparing this formula with (3) we see that
for yet another constant . Sending
we recover an exact formula
when is simple. Since almost all Hermitian matrices have simple spectrum (see Exercise 10 of Notes 3a), this gives the full spectral distribution of GUE, except for the issue of the unspecified constant.
Remark 1 In principle, this method should also recover the explicit normalising constant
in (1), but to do this it appears one needs to understand the volume of the fundamental domain of
with respect to the logarithm map, or equivalently to understand the volume of the unit ball of Hermitian matrices in the operator norm. I do not know of a simple way to compute this quantity (though it can be inferred from (1) and the above analysis). One can also recover the normalising constant through the machinery of determinantal processes, see below.
Remark 2 The above computation can be generalised to other
-conjugation-invariant ensembles
whose probability distribution is of the form
for some potential function
(where we use the spectral theorem to define
), yielding a density function for the spectrum of the form
Given suitable regularity conditions on
, one can then generalise many of the arguments in these notes to such ensembles. See this book by Deift for details.
— 2. The spectrum of gaussian matrices —
The above method also works for gaussian matrices , as was first observed by Dyson (though the final formula was first obtained by Ginibre, using a different method). Here, the density function is given by
where is a constant and
is Lebesgue measure on the space
of all complex
matrices. This is invariant under both left and right multiplication by unitary matrices, so in particular is invariant under unitary conjugations as before.
This matrix has
complex (generalised) eigenvalues
, which are usually distinct:
Exercise 3 Let
. Show that the space of matrices in
with a repeated eigenvalue has codimension
.
Unlike the Hermitian situation, though, there is no natural way to order these complex eigenvalues. We will thus consider all
possible permutations at once, and define the spectral density function
of
by duality and the formula
for all test functions . By the Riesz representation theorem, this uniquely defines
(as a distribution, at least), although the total mass of
is
rather than
due to the ambiguity in the spectrum.
Now we compute (up to constants). In the Hermitian case, the key was to use the factorisation
. This particular factorisation is of course unavailable in the non-Hermitian case. However, if the non-Hermitian matrix
has simple spectrum, it can always be factored instead as
, where
is unitary and
is upper triangular. Indeed, if one applies the Gram-Schmidt process to the eigenvectors of
and uses the resulting orthonormal basis to form
, one easily verifies the desired factorisation. Note that the eigenvalues of
are the same as those of
, which in turn are just the diagonal entries of
.
Exercise 4 Show that this factorisation is also available when there are repeated eigenvalues. (Hint: use the Jordan normal form.)
To use this factorisation, we first have to understand how unique it is, at least in the generic case when there are no repeated eigenvalues. As noted above, if , then the diagonal entries of
form the same set as the eigenvalues of
.
Now suppose we fix the diagonal of
, which amounts to picking an ordering of the
eigenvalues of
. The eigenvalues of
are
, and furthermore for each
, the eigenvector of
associated to
lies in the span of the last
basis vectors
of
, with a non-zero
coefficient (as can be seen by Gaussian elimination or Cramer’s rule). As
with
unitary, we conclude that for each
, the
column of
lies in the span of the eigenvectors associated to
. As these columns are orthonormal, they must thus arise from applying the Gram-Schmidt process to these eigenvectors (as discussed earlier). This argument also shows that once the diagonal entries
of
are fixed, each column of
is determined up to rotation by a unit phase. In other words, the only remaining freedom is to replace
by
for some unit diagonal matrix
, and then to replace
by
to counterbalance this change of
.
To summarise, the factorisation is unique up to specifying an enumeration
of the eigenvalues of
and right-multiplying
by diagonal unitary matrices, and then conjugating
by the same matrix. Given a matrix
, we may apply these symmetries randomly, ending up with a random enumeration
of the eigenvalues of
(whose distribution invariant with respect to permutations) together with a random factorisation
such that
has diagonal entries
in that order, and the distribution of
is invariant under conjugation by diagonal unitary matrices. Also, since
is itself invariant under unitary conjugations, we may also assume that
is distributed uniformly according to the Haar measure of
, and independently of
.
To summarise, the gaussian matrix ensemble , together with a randomly chosen enumeration
of the eigenvalues, can almost surely be factorised as
, where
is an upper-triangular matrix with diagonal entries
, distributed according to some distribution
which is invariant with respect to conjugating by diagonal unitary matrices, and
is uniformly distributed according to the Haar measure of
, independently of
.
Now let be an upper triangular matrix with complex entries whose entries
are distinct. As in the previous section, we consider the probability
On the one hand, since the space of complex
matrices has
real dimensions, we see from (9) that this expression is equal to
for some constant .
Now we compute (6) using the factorisation . Suppose that
, so
As the eigenvalues of
are
, which are assumed to be distinct, we see (from the inverse function theorem) that for
small enough,
has eigenvalues
. With probability
, the diagonal entries of
are thus
(in that order). We now restrict to this event (the
factor will eventually be absorbed into one of the unspecified constants).
Let be eigenvector of
associated to
, then the Gram-Schmidt process applied to
(starting at
and working backwards to
) gives the standard basis
(in reverse order). By the inverse function theorem, we thus see that we have eigenvectors
of
, which when the Gram-Schmidt process is applied, gives a perturbation
in reverse order. This gives a factorisation
in which
, and hence
. This is however not the most general factorisation available, even after fixing the diagonal entries of
, due to the freedom to right-multiply
by diagonal unitary matrices
. We thus see that the correct ansatz here is to have
for some diagonal unitary matrix .
In analogy with the GUE case, we can use the inverse function theorem and make the more precise ansatz
where is skew-Hermitian with zero diagonal and size
,
is diagonal unitary, and
is an upper triangular matrix of size
. From the invariance
we see that
is distributed uniformly across all diagonal unitaries. Meanwhile, from the unitary conjugation invariance,
is distributed according to a constant multiple of
times Lebesgue measure
on the
-dimensional space of skew Hermitian matrices with zero diagonal; and from the definition of
,
is distributed according to a constant multiple of the measure
where is Lebesgue measure on the
-dimensional space of upper-triangular matrices. Furthermore, the invariances ensure that the random variables
are distributed independently. Finally, we have
Thus we may rewrite (6) as
for some (the
integration being absorbable into this constant
). We can Taylor expand
and so we can bound (8) above and below by expressions of the form
The Lebesgue measure is invariant under translations by upper triangular matrices, so we may rewrite the above expression as
where is the strictly lower triangular component of
.
The next step is to make the (linear) change of variables . We check dimensions:
ranges in the space
of skew-adjoint Hermitian matrices with zero diagonal, which has dimension
, as does the space of strictly lower-triangular matrices, which is where
ranges. So we can in principle make this change of variables, but we first have to compute the Jacobian of the transformation (and check that it is non-zero). For this, we switch to coordinates. Write
and
. In coordinates, the equation
becomes
or equivalently
Thus for instance
etc. We then observe that the transformation matrix from to
is triangular, with diagonal entries given by
for
. The Jacobian of the (complex-linear) map
is thus given by
which is non-zero by the hypothesis that the are distinct. We may thus rewrite (9) as
where is Lebesgue measure on strictly lower-triangular matrices. The integral here is equal to
for some constant
. Comparing this with (6), cancelling the factor of
, and sending
, we obtain the formula
for some constant . We can expand
If we integrate out the off-diagonal variables for
, we see that the density function for the diagonal entries
of
is proportional to
Since these entries are a random permutation of the eigenvalues of , we conclude the Ginibre formula
for the joint density of the eigenvalues of a gaussian random matrix, where is a constant.
Remark 5 Given that (1) can be derived using Dyson Brownian motion, it is natural to ask whether (10) can be derived by a similar method. It seems that in order to do this, one needs to consider a Dyson-like process not just on the eigenvalues
, but on the entire triangular matrix
(or more precisely, on the moduli space formed by quotienting out the action of conjugation by unitary diagonal matrices). Unfortunately the computations seem to get somewhat complicated, and we do not present them here.
— 3. Mean field approximation —
We can use the formula (1) for the joint distribution to heuristically derive the semicircular law, as follows.
It is intuitively plausible that the spectrum should concentrate in regions in which
is as large as possible. So it is now natural to ask how to optimise this function. Note that the expression in (1) is non-negative, and vanishes whenever two of the
collide, or when one or more of the
go off to infinity, so a maximum should exist away from these degenerate situations.
We may take logarithms and write
where is a constant whose exact value is not of importance to us. From a mathematical physics perspective, one can interpret (11) as a Hamiltonian for
particles at positions
, subject to a confining harmonic potential (these are the
terms) and a repulsive logarithmic potential between particles (these are the
terms).
Our objective is now to find a distribution of that minimises this expression.
We know from previous notes that the should have magnitude
. Let us then heuristically make a mean field approximation, in that we approximate the discrete spectral measure
by a continuous probability measure
. (Secretly, we know from the semi-circular law that we should be able to take
, but pretend that we do not know this fact yet.) Then we can heuristically approximate (11) as
and so we expect the distribution to minimise the functional
One can compute the Euler-Lagrange equations of this functional:
Exercise 6 Working formally, and assuming that
is a probability measure that minimises (12), argue that
for some constant
and all
in the support of
. For all
outside of the support, establish the inequality
There are various ways we can solve this equation for ; we sketch here a complex-analytic method. Differentiating in
, we formally obtain
on the support of . But recall that if we let
be the Stieltjes transform of the probability measure , then we have
and
We conclude that
for all , which we rearrange as
This makes the function entire (it is analytic in the upper half-plane, obeys the symmetry
, and has no jump across the real line). On the other hand, as
as
,
goes to
at infinity. Applying Liouville’s theorem, we conclude that
is constant, thus we have the familiar equation
which can then be solved to obtain the semi-circular law as in previous notes.
Remark 7 Recall from Notes 3b that Dyson Brownian motion can be used to derive the formula (1). One can then interpret the Dyson Brownian motion proof of the semi-circular law for GUE in Notes 4 as a rigorous formalisation of the above mean field approximation heuristic argument.
One can perform a similar heuristic analysis for the spectral measure of a random gaussian matrix, giving a description of the limiting density:
Exercise 8 Using heuristic arguments similar to those above, argue that
should be close to a continuous probability distribution
obeying the equation
on the support of
, for some constant
, with the inequality
outside of this support. Using the Newton potential
for the fundamental solution of the two-dimensional Laplacian
, conclude (non-rigorously) that
is equal to
on its support.
Also argue thatshould be rotationally symmetric. Use (13) and Green’s formula to argue why the support of
should be simply connected, and then conclude (again non-rigorously) the circular law
We will see more rigorous derivations of the circular law later in these notes, and also in subsequent notes.
— 4. Determinantal form of the GUE spectral distribution —
In a previous section, we showed (up to constants) that the density function for the eigenvalues
of GUE was given by the formula (1).
As is well known, the Vandermonde determinant that appears in (1) can be expressed up to sign as a determinant of an
matrix, namely the matrix
. Indeed, this determinant is clearly a polynomial of degree
in
which vanishes whenever two of the
agree, and the claim then follows from the factor theorem (and inspecting a single coefficient of the Vandermonde determinant, e.g. the
coefficient, to get the sign).
We can square the above fact (or more precisely, multiply the above matrix matrix by its adjoint) and conclude that is the determinant of the matrix
More generally, if are any sequence of polynomials, in which
has degree
, then we see from row operations that the determinant of
is a non-zero constant multiple of (with the constant depending on the leading coefficients of the
), and so the determinant of
is a non-zero constant multiple of . Comparing this with (1), we obtain the formula
for some non-zero constant .
This formula is valid for any choice of polynomials of degree
. But the formula is particularly useful when we set
equal to the (normalised) Hermite polynomials, defined by applying the Gram-Schmidt process in
to the polynomials
for
to yield
. (Equivalently, the
are the orthogonal polynomials associated to the measure
.) In that case, the expression
becomes the integral kernel of the orthogonal projection operator in
to the span of the
, thus
for all , and so
is now a constant multiple of
The reason for working with orthogonal polynomials is that we have the trace identity
which reflects the identity . These two formulae have an important consequence:
Lemma 9 (Determinantal integration formula) Let
be any symmetric rapidly decreasing function obeying (16), (17). Then for any
, one has
Remark 10 This remarkable identity is part of the beautiful algebraic theory of determinantal processes, which I discuss further in this blog post.
Proof: We induct on . When
this is just (16). Now assume that
and that the claim has already been proven for
. We apply cofactor expansion to the bottom row of the determinant
. This gives a principal term
plus a sum of additional terms, the
term of which is of the form
Using (16), the principal term (19) gives a contribution of to (18). For each nonprincipal term (20), we use the multilinearity of the determinant to absorb the
term into the
column of the matrix. Using (17), we thus see that the contribution of (20) to (18) can be simplified as
which after row exchange, simplifies to . The claim follows.
In particular, if we iterate the above lemma using the Fubini-Tonelli theorem, we see that
On the other hand, if we extend the probability density function symmetrically from the Weyl chamber
to all of
, its integral is also
. Since
is clearly symmetric in the
, we can thus compare constants and conclude the Gaudin-Mehta formula
More generally, if we define to be the function
then the above formula shows that is the
-point correlation function for the spectrum, in the sense that
for any test function supported in the region
.
In particular, if we set , we obtain the explicit formula
for the expected empirical spectral measure of . Equivalently after renormalising by
, we have
It is thus of interest to understand the kernel better.
To do this, we begin by recalling that the functions were obtained from
by the Gram-Schmidt process. In particular, each
is orthogonal to the
for all
. This implies that
is orthogonal to
for
. On the other hand,
is a polynomial of degree
, so
must lie in the span of
for
. Combining the two facts, we see that
must be a linear combination of
, with the
coefficient being non-trivial. We rewrite this fact in the form
for some real numbers (with
). Taking inner products with
and
we see that
and
(with the convention ).
We will continue the computation of later. For now, we we pick two distinct real numbers
and consider the Wronskian-type expression
Using (24), (26), we can write this as
or in other words
We telescope this and obtain the Christoffel-Darboux formula for the kernel (15):
Sending using L’Hopital’s rule, we obtain in particular that
Inserting this into (23), we see that if we want to understand the expected spectral measure of GUE, we should understand the asymptotic behaviour of and the associated constants
. For this, we need to exploit the specific properties of the gaussian weight
. In particular, we have the identity
so upon integrating (25) by parts, we have
As has degree at most
, the first term vanishes by the orthonormal nature of the
, thus
To compute this, let us denote the leading coefficient of as
. Then
is equal to
plus lower-order terms, and so we have
On the other hand, by inspecting the coefficient of (24) we have
Combining the two formulae (and making the sign convention that the are always positive), we see that
and
Meanwhile, a direct computation shows that , and thus by induction
A similar method lets us compute the . Indeed, taking inner products of (24) with
and using orthonormality we have
which upon integrating by parts using (29) gives
As is of degree strictly less than
, the integral vanishes by orthonormality, thus
. The identity (24) thus becomes Hermite recurrence relation
Another recurrence relation arises by considering the integral
On the one hand, as has degree at most
, this integral vanishes if
by orthonormality. On the other hand, integrating by parts using (29), we can write the integral as
If , then
has degree less than
, so the integral again vanishes. Thus the integral is non-vanishing only when
. Using (30), we conclude that
We can combine (32) with (31) to obtain the formula
which together with the initial condition gives the explicit representation
for the Hermite polynomials. Thus, for instance, at one sees from Taylor expansion that
when is odd.
In principle, the formula (33), together with (28), gives us an explicit description of the kernel (and thus of
, by (23)). However, to understand the asymptotic behaviour as
, we would have to understand the asymptotic behaviour of
as
, which is not immediately discernable by inspection. However, one can obtain such asymptotics by a variety of means. We give two such methods here: a method based on ODE analysis, and a complex-analytic method, based on the method of steepest descent.
We begin with the ODE method. Combining (31) with (32) we see that each polynomial obeys the Hermite differential equation
If we look instead at the Hermite functions , we obtain the differential equation
where is the harmonic oscillator operator
Note that the self-adjointness of here is consistent with the orthogonal nature of the
.
Exercise 11 Use (15), (28), (33), (31), (32) to establish the identities
and thus by (23)
It is thus natural to look at the rescaled functions
which are orthonormal in and solve the equation
where is the semiclassical harmonic oscillator operator
thus
The projection is then the spectral projection operator of
to
. According to semi-classical analysis, with
being interpreted as analogous to Planck’s constant, the operator
has symbol
, where
is the momentum operator, so the projection
is a projection to the region
of phase space, or equivalently to the region
. In the semi-classical limit
, we thus expect the diagonal
of the normalised projection
to be proportional to the projection of this region to the
variable, i.e. proportional to
. We are thus led to the semi-circular law via semi-classical analysis.
It is possible to make the above argument rigorous, but this would require developing the theory of microlocal analysis, which would be overkill given that we are just dealing with an ODE rather than a PDE here (and an extremely classical ODE at that). We instead use a more basic semiclassical approximation, the WKB approximation, which we will make rigorous using the classical method of variation of parameters (one could also proceed using the closely related Prüfer transformation, which we will not detail here). We study the eigenfunction equation
where we think of as being small, and
as being close to
. We rewrite this as
where , where we will only work in the “classical” region
(so
) for now.
Recall that the general solution to the constant coefficient ODE is given by
. Inspired by this, we make the ansatz
where is the antiderivative of
. Differentiating this, we have
Because we are representing a single function by two functions
, we have the freedom to place an additional constraint on
. Following the usual variation of parameters strategy, we will use this freedom to eliminate the last two terms in the expansion of
, thus
We can now differentiate again and obtain
Comparing this with (37) we see that
Combining this with (38), we obtain equations of motion for and
:
We can simplify this using the integrating factor substitution
The point of doing all these transformations is that the role of the parameter no longer manifests itself through amplitude factors, and instead only is present in a phase factor. In particular, we have
on any compact interval in the interior of the classical region
(where we allow implied constants to depend on
), which by Gronwall’s inequality gives the bounds
on this interval . We can then insert these bounds into (39), (40) again and integrate by parts (taking advantage of the non-stationary nature of
) to obtain the improved bounds
on this interval. (More precise asymptotic expansions can be obtained by iterating this procedure, but we will not need them here.) This is already enough to get the asymptotics that we need:
Exercise 12 Use (36) to Show that on any compact interval
in
, the density of
is given by
where
are as above with
and
. Combining this with (41), (34), (35), and Stirling’s formula, conclude that
converges in the vague topology to the semicircular law
. (Note that once one gets convergence inside
, the convergence outside of
can be obtained for free since
and
are both probability measures.
We now sketch out the approach using the method of steepest descent. The starting point is the Fourier inversion formula
which upon repeated differentiation gives
and thus by (33)
and thus
where
where we use a suitable branch of the complex logarithm to handle the case of negative .
The idea of the principle of steepest descent is to shift the contour of integration to where the real part of is as small as possible. For this, it turns out that the stationary points of
play a crucial role. A brief calculation using the quadratic formula shows that there are two such stationary points, at
When ,
is purely imaginary at these stationary points, while for
the real part of
is negative at both points. One then draws a contour through these two stationary points in such a way that near each such point, the imaginary part of
is kept fixed, which keeps oscillation to a minimum and allows the real part to decay as steeply as possible (which explains the name of the method). After a certain tedious amount of computation, one obtains the same type of asymptotics for
that were obtained by the ODE method when
(and exponentially decaying estimates for
).
Exercise 13 Let
,
be functions which are analytic near a complex number
, with
and
. Let
be a small number, and let
be the line segment
, where
is a complex phase such that
is a negative real. Show that for
sufficiently small, one has
as
. This is the basic estimate behind the method of steepest descent; readers who are also familiar with the method of stationary phase may see a close parallel.
Remark 14 The method of steepest descent requires an explicit representation of the orthogonal polynomials as contour integrals, and as such is largely restricted to the classical orthogonal polynomials (such as the Hermite polynomials). However, there is a non-linear generalisation of the method of steepest descent developed by Deift and Zhou, in which one solves a matrix Riemann-Hilbert problem rather than a contour integral; see this book by Deift for details. Using these sorts of tools, one can generalise much of the above theory to the spectral distribution of
-conjugation-invariant discussed in Remark 2, with the theory of Hermite polynomials being replaced by the more general theory of orthogonal polynomials; this is discussed in the above book of Deift, as well as the more recent book of Deift and Gioev.
The computations performed above for the diagonal kernel can be summarised by the asymptotic
whenever is fixed and
, and
is the semi-circular law distribution. It is reasonably straightforward to generalise these asymptotics to the off-diagonal case as well, obtaining the more general result
for fixed and
, where
is the Dyson sine kernel
In the language of semi-classical analysis, what is going on here is that the rescaling in the left-hand side of (42) is transforming the phase space region to the region
in the limit
, and the projection to the latter region is given by the Dyson sine kernel. A formal proof of (42) can be given by using either the ODE method or the steepest descent method to obtain asymptotics for Hermite polynomials, and thence (via the Christoffel-Darboux formula) to asymptotics for
; we do not give the details here, but see for instance the recent book of Anderson, Guionnet, and Zeitouni.
From (42) and (21), (22) we obtain the asymptotic formula
for the local statistics of eigenvalues. By means of further algebraic manipulations (using the general theory of determinantal processes), this allows one to control such quantities as the distribution of eigenvalue gaps near , normalised at the scale
, which is the average size of these gaps as predicted by the semicircular law. For instance, for any
, one can show (basically by the above formulae combined with the inclusion-exclusion principle) that the proportion of eigenvalues
with normalised gap
less than
converges as
to
, where
is defined by the formula
, and
is the integral operator with kernel
(this operator can be verified to be trace class, so the determinant can be defined in a Fredholm sense). See for instance this book of Mehta (and my blog post on determinantal processes describe a finitary version of the inclusion-exclusion argument used to obtain such a result).
Remark 15 One can also analyse the distribution of the eigenvalues at the edge of the spectrum, i.e. close to
. This ultimately hinges on understanding the behaviour of the projection
near the corners
of the phase space region
, or of the Hermite polynomials
for
close to
. For instance, by using steepest descent methods, one can show that
as
for any fixed
, where
is the Airy function
This asymptotic and the Christoffel-Darboux formula then gives the asymptotic
for any fixed
, where
is the Airy kernel
(Aside: Semiclassical heuristics suggest that the rescaled kernel (43) should correspond to projection to the parabolic region of phase space
, but I do not know of a connection between this region and the Airy kernel; I am not sure whether semiclassical heuristics are in fact valid at this scaling regime. On the other hand, these heuristics do explain the emergence of the length scale
that emerges in (43), as this is the smallest scale at the edge which occupies a region in
consistent with the Heisenberg uncertainty principle.) This then gives an asymptotic description of the largest eigenvalues of a GUE matrix, which cluster in the region
. For instance, one can use the above asymptotics to show that the largest eigenvalue
of a GUE matrix obeys the Tracy-Widom law
for any fixed
, where
is the integral operator with kernel
. See for instance the recent book of Anderson, Guionnet, and Zeitouni.
— 5. Determinantal form of the gaussian matrix distribution —
One can perform an analogous analysis of the joint distribution function (10) of gaussian random matrices. Indeed, given any family of polynomials, with each
of degree
, much the same arguments as before show that (10) is equal to a constant multiple of
One can then select to be orthonormal in
. Actually in this case, the polynomials are very simple, being given explicitly by the formula
Exercise 16 Verify that the
are indeed orthonormal, and then conclude that (10) is equal to
, where
Conclude further that the
-point correlation functions
are given as
Exercise 17 Show that as
, one has
and deduce that the expected spectral measure
converges vaguely to the circular measure
; this is a special case of the circular law.
Exercise 18 For any
and
, show that
as
. This formula (in principle, at least) describes the asymptotic local
-point correlation functions of the spectrum of gaussian matrices.
Remark 19 One can use the above formulae as the starting point for many other computations on the spectrum of random gaussian matrices; to give just one example, one can show that expected number of eigenvalues which are real is of the order of
(see this paper of Edelman for more precise results of this nature). It remains a challenge to extend these results to more general ensembles than the gaussian ensemble.

24 comments
Comments feed for this article
24 February, 2010 at 11:48 am
Anonymous
There’s a minor typo (“frac” should be “\frac”) in the statement of Exercise 9.
[Corrected, thanks – T.]
26 February, 2010 at 6:49 pm
Anonymous
Dear Prof. Tao,
Thank you for the great post.
Which course are you going to teach next semester? If you give a hint, we can start to read related materials. your lecture notes are terrific but requires strong background.
Thanks
5 March, 2010 at 1:47 pm
254A, Notes 7: The least singular value « What’s new
[…] of a gaussian random matrix can be computed explicitly by techniques similar to those employed in Notes 6. In particular, if is a real gaussian matrix (with all entries iid with distribution ), it was […]
9 August, 2010 at 10:31 am
Anonymous
In deriving the pdf for GUE, “We can thus use the inverse function theorem in this local region of parameter space and make the ansatz ….”
How is this true? Is there any reference to detailing this step?
9 August, 2010 at 12:46 pm
Terence Tao
As stated immediately after that quote, one computes the Jacobian of at
at 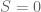 (and
(and  equal to a diagonal unitary) and verifies that it is non-zero. This already gives the desired parameterisation in the
equal to a diagonal unitary) and verifies that it is non-zero. This already gives the desired parameterisation in the 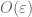 neighbourhood of any diagonal unitary
neighbourhood of any diagonal unitary  , from the inverse function theorem (it may be convenient here to scale out the
, from the inverse function theorem (it may be convenient here to scale out the  and look at the map
and look at the map  instead). Since we already know
instead). Since we already know  lies within
lies within 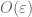 of a diagonal unitary, the claim follows.
of a diagonal unitary, the claim follows.
23 October, 2010 at 12:57 pm
The Dyson and Airy kernels of GUE via semiclassical analysis « What’s new
[…] standard computation (given for instance in these lecture notes of mine) gives the Ginebre […]
4 December, 2010 at 10:44 pm
Anonymous
Dear Prof. Tao,
I don’t quite understand the argument after equation (20). You said you want to absorb K_n(x_l,x_{k+1}) into the l-th column. But isn’t the l-th column omitted in the matrix that follows? Maybe you meant the k+1th column? But I couldn’t figure out how to make it work.
[Corrected, thanks. The strategy is to get to the point where one can use the identity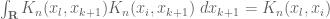 .]
.]
5 December, 2010 at 11:32 am
Anonymous
Ah I see. You are integrating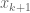 partially first. Thanks!
partially first. Thanks!
2 November, 2011 at 1:30 pm
Smolin (2011) | Research Notebook
[…] is a real valued random matrix from the GOE ensemble whose eigenvalues for subscribe to Dyson Brownian […]
15 June, 2012 at 5:31 am
vishwajeet singh
Dear Dr Tao,
I have just started my venture into Random matrix. What puzzles me is that all the Gaussian ensembles assume zero mean entries. How does the entire formulation change when the entries do not have zero mean? i.e the entries are Normal(\mu,\sigma). How does the distribution of the eigenvalues change ??
Thanks.
12 November, 2012 at 7:59 am
A direct proof of the stationarity of the Dyson sine process under Dyson Brownian motion « What’s new
[…] where are the (normalised) Hermite polynomials; see this previous blog post for details. […]
17 March, 2013 at 8:26 pm
Ilya Razenshteyn
My feeling that is (43) the normalization is wrong. There should be .
.
[Corrected, thanks – T.]
5 January, 2014 at 3:09 am
Anonymous
In Section 2, doesn’t conjugation by a permutation matrix make T lose its upper diagonal structure?
5 January, 2014 at 10:16 am
Terence Tao
Gah, you’re right. Fortunately, the permutation symmetry for T is not actually needed in the argument, provided that one augments the given data (i.e. the matrix G to be factorised) by also attaching a (randomly chosen) enumeration of the eigenvalues of G, and demanding that T has the diagonal entries
of the eigenvalues of G, and demanding that T has the diagonal entries  in that order. While T indeed does not have permutation symmetry, the data (the pair consisting of
in that order. While T indeed does not have permutation symmetry, the data (the pair consisting of  and the enumeration
and the enumeration  ) retains the permutation symmetry, which is what is actually used in the argument. I’ve rewritten the text to reflect this.
) retains the permutation symmetry, which is what is actually used in the argument. I’ve rewritten the text to reflect this.
2 March, 2015 at 1:59 pm
Chansoo Lee
Dear Professor Tao,
Does the fact that you used a heuristic mean field approximation imply that in general, you can’t find the actual eigenvalues that maximize the pdf for n > 4?
Thanks
2 March, 2015 at 8:36 pm
Terence Tao
The points that maximise the pdf are known as Fekete points; asymptotics for these points are known (by using a more rigorous version of the mean field approximation), but I doubt that there is any closed form for them.
29 June, 2016 at 3:10 pm
Jhon Manugal
I know it’s a cheap trick, but you should definitely use raising and lowering operators since you are dealing with Hermite polynomials. And there’s probably an representation or
representation or  in there but don’t take my word for it. I appreciate you doing WKB approximation in a rigorous way but I had trouble recognizing it compared to what the physicists actually write. So Ratner theorem, WKB approximation and everything else is the same.
in there but don’t take my word for it. I appreciate you doing WKB approximation in a rigorous way but I had trouble recognizing it compared to what the physicists actually write. So Ratner theorem, WKB approximation and everything else is the same.
5 January, 2017 at 11:27 am
Ramis Movassagh
Hi Terry, A minor typo perhaps.
On the 5th line, in the paragraph above Eq. 2 starting with ” Let D be…”, M should probably be M_n.
[Corrected, thanks -T.]
8 January, 2017 at 9:54 am
Ramis Movassagh
Hi Terry,
I very much like this post as always.
Minor typos perhaps:
The first paragraph below Eq. 11 the I think instead of 1/|\lambda_i – \lambda_j|, it should say \log 1/|\lambda_i – \lambda_j|.
Also three lines below “\lambda_i should be have…” to “\lambda_i should have…”
[Corrected, thanks – T.]
8 April, 2019 at 8:07 am
Anonymous
Dear professor Tao
Right after making the ansatz {U=\exp(\epsilon S)R} you say
As {U} is distributed using Haar measure on {U(n)}, {S} is (locally) distributed using {\epsilon^{n^2-n}} times a constant multiple of Lebesgue measure on the space {W} of skew-adjoint matrices with zero diagonal, which has dimension {n^2-n}.
Is there any refference to this step in details? Do i need to use the Baker–Campbell–Hausdorff formula?
8 April, 2019 at 11:10 am
Terence Tao
Oops, there was a factor of missing in front of
missing in front of 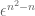 . One can indeed proceed using BCH: the fact that Haar measure is invariant under rotations of the form
. One can indeed proceed using BCH: the fact that Haar measure is invariant under rotations of the form  for some skew-adjoint
for some skew-adjoint  with zero diagonal means that the distribution of S is invariant under a transformation which looks like translation by
with zero diagonal means that the distribution of S is invariant under a transformation which looks like translation by  plus errors of size
plus errors of size  (and whose derivatives also have size o(1)), so after taking Jacobians we see that the density of this distribution is constant up to factors of
(and whose derivatives also have size o(1)), so after taking Jacobians we see that the density of this distribution is constant up to factors of  .
.
10 May, 2019 at 8:37 am
The alternative hypothesis for unitary matrices | What's new
[…] the the Vandermonde determinant; see for instance this previous blog post for the derivation of a very similar formula for the GUE distribution, which can be adapted to CUE […]
3 January, 2021 at 12:50 am
tpfly
Dear Professor Tao,
In Exercise 4 should there be a factor of 2 before the logarithmic potential? Otherwise taking the Laplacian we would get $\rho(z)=2/\pi$ on its support.
[Corrected, thanks – T.]
18 January, 2021 at 1:56 am
tpfly
Dear Professor Tao,
The HTML code has been broken since last modification, and some latex formula do not parse.
I think there are still some more mistakes in this post and in the corresponding chapter of “topics in RMT”:
1): Using (34), I found (35) should be
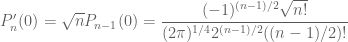
when n is odd. Comparing with (35), the sign is different (the power of -1 should be (n-1)/2).
2) The rescaled functions should be defined as
should be defined as  which are orthonormal. The scale
which are orthonormal. The scale 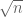 outside of the functions do not make them orthonormal.
outside of the functions do not make them orthonormal. should be
should be  instead of
instead of  .
. should be
should be 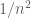 .
. (in the sketch of steepest descent), the factor
(in the sketch of steepest descent), the factor  is missing.
is missing.
Then the following 3), 4), 5) are related to this.
3) In the book, the harmonic oscillator operator on
4) In eq.(36), the coefficient of
5) In the integral formula of
6) In Exercise 12, the density of should be
should be
[Corrected, thanks – T.]