One of the most fundamental concepts in Euclidean geometry is that of the measure of a solid body
in one or more dimensions. In one, two, and three dimensions, we refer to this measure as the length, area, or volume of
respectively. In the classical approach to geometry, the measure of a body was often computed by partitioning that body into finitely many components, moving around each component by a rigid motion (e.g. a translation or rotation), and then reassembling those components to form a simpler body which presumably has the same area. One could also obtain lower and upper bounds on the measure of a body by computing the measure of some inscribed or circumscribed body; this ancient idea goes all the way back to the work of Archimedes at least. Such arguments can be justified by an appeal to geometric intuition, or simply by postulating the existence of a measure
that can be assigned to all solid bodies
, and which obeys a collection of geometrically reasonable axioms. One can also justify the concept of measure on “physical” or “reductionistic” grounds, viewing the measure of a macroscopic body as the sum of the measures of its microscopic components.
With the advent of analytic geometry, however, Euclidean geometry became reinterpreted as the study of Cartesian products of the real line
. Using this analytic foundation rather than the classical geometrical one, it was no longer intuitively obvious how to define the measure
of a general subset
of
; we will refer to this (somewhat vaguely defined) problem of writing down the “correct” definition of measure as the problem of measure. (One can also pose the problem of measure on other domains than Euclidean space, such as a Riemannian manifold, but we will focus on the Euclidean case here for simplicity.)
To see why this problem exists at all, let us try to formalise some of the intuition for measure discussed earlier. The physical intuition of defining the measure of a body to be the sum of the measure of its component “atoms” runs into an immediate problem: a typical solid body would consist of an infinite (and uncountable) number of points, each of which has a measure of zero; and the product
is indeterminate. To make matters worse, two bodies that have exactly the same number of points, need not have the same measure. For instance, in one dimension, the intervals
and
are in one-to-one correspondence (using the bijection
from
to
), but of course
is twice as long as
. So one can disassemble
into an uncountable number of points and reassemble them to form a set of twice the length.
Of course, one can point to the infinite (and uncountable) number of components in this disassembly as being the cause of this breakdown of intuition, and restrict attention to just finite partitions. But one still runs into trouble here for a number of reasons, the most striking of which is the Banach-Tarski paradox, which shows that the unit ball in three dimensions can be disassembled into a finite number of pieces (in fact, just five pieces suffice), which can then be reassembled (after translating and rotating each of the pieces) to form two disjoint copies of the ball
. (The paradox only works in three dimensions and higher, for reasons having to do with the property of amenability; see this blog post for further discussion of this interesting topic, which is unfortunately too much of a digression from the current subject.)
Here, the problem is that the pieces used in this decomposition are highly pathological in nature; among other things, their construction requires use of the axiom of choice. (This is in fact necessary; there are models of set theory without the axiom of choice in which the Banach-Tarski paradox does not occur, thanks to a famous theorem of Solovay.) Such pathological sets almost never come up in practical applications of mathematics. Because of this, the standard solution to the problem of measure has been to abandon the goal of measuring every subset of
, and instead to settle for only measuring a certain subclass of “non-pathological” subsets of
, which are then referred to as the measurable sets. The problem of measure then divides into several subproblems:
- What does it mean for a subset
of
to be measurable?
- If a set
is measurable, how does one define its measure?
- What nice properties or axioms does measure (or the concept of measurability) obey?
- Are “ordinary” sets such as cubes, balls, polyhedra, etc. measurable?
- Does the measure of an “ordinary” set equal the “naive geometric measure” of such sets? (e.g. is the measure of an
rectangle equal to
?)
These questions are somewhat open-ended in formulation, and there is no unique answer to them; in particular, one can expand the class of measurable sets at the expense of losing one or more nice properties of measure in the process (e.g. finite or countable additivity, translation invariance, or rotation invariance). However, there are two basic answers which, between them, suffice for most applications. The first is the concept of Jordan measure of a Jordan measurable set, which is a concept closely related to that of the Riemann integral (or Darboux integral). This concept is elementary enough to be systematically studied in an undergraduate analysis course, and suffices for measuring most of the “ordinary” sets (e.g. the area under the graph of a continuous function) in many branches of mathematics. However, when one turns to the type of sets that arise in analysis, and in particular those sets that arise as limits (in various senses) of other sets, it turns out that the Jordan concept of measurability is not quite adequate, and must be extended to the more general notion of Lebesgue measurability, with the corresponding notion of Lebesgue measure that extends Jordan measure. With the Lebesgue theory (which can be viewed as a completion of the Jordan-Darboux-Riemann theory), one keeps almost all of the desirable properties of Jordan measure, but with the crucial additional property that many features of the Lebesgue theory are preserved under limits (as exemplified in the fundamental convergence theorems of the Lebesgue theory, such as the monotone convergence theorem and the dominated convergence theorem, which do not hold in the Jordan-Darboux-Riemann setting). As such, they are particularly well suited for applications in analysis, where limits of functions or sets arise all the time. (There are other ways to extend Jordan measure and the Riemann integral, but the Lebesgue approach handles limits better than the other alternatives, and so has become the standard approach in analysis.)
In the rest of the course, we will formally define Lebesgue measure and the Lebesgue integral, as well as the more general concept of an abstract measure space and the associated integration operation. In the rest of this post, we will discuss the more elementary concepts of Jordan measure and the Riemann integral. This material will eventually be superceded by the more powerful theory to be treated in the main body of the course; but it will serve as motivation for that later material, as well as providing some continuity with the treatment of measure and integration in undergraduate analysis courses.
— 1. Elementary measure —
Before we discuss Jordan measure, we discuss the even simpler notion of elementary measure, which allows one to measure a very simple class of sets, namely the elementary sets (finite unions of boxes).
Definition 1 (Intervals, boxes, elementary sets) An interval is a subset of
of the form
,
,
, or
, where
are real numbers. We define the length
of an interval
to be
. (Note we allow degenerate intervals of zero length.) A box in
is a Cartesian product
of
intervals
(not necessarily of the same length), thus for instance an interval is a one-dimensional box. The volume
of such a box
is defined as
. An elementary set is any subset of
which is the union of a finite number of boxes.
Exercise 1 (Boolean closure) Show that if
are elementary sets, then the union
, the intersection
, and the set theoretic difference
, and the symmetric difference
are also elementary. If
, show that the translate
is also an elementary set.
We now give each elementary set a measure.
Lemma 2 (Measure of an elementary set) Let
be an elementary set.
can be expressed as the finite union of disjoint boxes.
- If
is partitioned as the finite union
of disjoint boxes, then the quantity
is independent of the partition. In other words, given any other partition
of
, one has
.
We refer to
as the elementary measure of
. (We occasionally write
as
to emphasise the
-dimensional nature of the measure.) Thus, for example, the elementary measure of
is
.
Proof: We first prove (1.) in the one-dimensional case . Given any finite collection of intervals
, one can place the
endpoints of these intervals in increasing order (discarding repetitions). Looking at the open intervals between these endpoints, together with the endpoints themselves (viewed as intervals of length zero), we see that there exists a finite collection of disjoint intervals
such that each of the
are a union of some subcollection of the
. This already gives (1.) when
. To prove the higher dimensional case, we express
as the union
of boxes
. For each
, we use the one-dimensional argument to express
as the union of subcollections of a collection
of disjoint intervals. Taking Cartesian products, we can express the
as finite unions of boxes
, where
for all
. Such boxes are all disjoint, and the claim follows.
To prove (2.) we use a discretisation argument. Observe (exercise!) that for any interval , the length of
can be recovered by the limiting formula
where and
denotes the cardinality of a finite set
. Taking Cartesian products, we see that
for any box , and in particular that
Denoting the right-hand side as , we obtain the claim (2.).
Exercise 2 Give an alternate proof of part (2.) of the above lemma by showing that any two partitions of
into boxes admit a mutual refinement into boxes that arise from taking Cartesian products of elements from finite collections of disjoint intervals.
Remark 1 One might be tempted to now define the measure
of an arbitrary set
by the formula
since this worked well for elementary sets. However, this definition is not particularly satisfactory for a number of reasons. Firstly, one can concoct examples in which the limit does not exist (Exercise!). Even when the limit does exist, this concept does not obey reasonable properties such as translation invariance. For instance, if
and
, then this definition would give
a measure of
, but would give the translate
a measure of zero. Nevertheless, the formula (1) will be valid for all Jordan measurable sets (see Exercise 13). It also makes precise an important intuition, namely that the continuous concept of measure can be viewed as a limit of the discrete concept of (normalised) cardinality. (Another way to obtain continuous measure as the limit of discrete measure is via Monte Carlo integration, although in order to rigorously introduce the probability theory needed to set up Monte Carlo integration properly, one already needs to develop a large part of measure theory, so this perspective, while intuitive, is not suitable for foundational purposes.)
From the definitions, it is clear that is a non-negative real number for every elementary set
, and that
whenever and
are disjoint elementary sets. We refer to the latter property as finite additivity; by induction it also implies that
whenever are disjoint elementary sets. We also have the obvious degenerate case
Finally, elementary measure clearly extends the notion of volume, in the sense that
for all boxes .
From non-negativity and finite additivity (and Exercise 1) we conclude the monotonicity property
whenever are nested elementary sets. From this and finite additivity (and Exercise 1) we easily obtain the finite subadditivity property
whenever are elementary sets (not necessarily disjoint); by induction one then has
whenever are elementary sets (not necessarily disjoint).
It is also clear from the definition that we have the translation invariance
for all elementary sets and
.
These properties in fact define elementary measure up to normalisation:
Exercise 3 (Uniqueness of elementary measure) Let
. Let
be a map from the collection
of elementary subsets of
to the nonnegative reals that obeys the non-negativity, finite additivity, and translation invariance properties. Show that there exists a constant
such that
for all elementary sets
. In particular, if we impose the additional normalisation
, then
. (Hint: Set
, and then compute
for any positive integer
.)
Exercise 4 Let
, and let
,
be elementary sets. Show that
is elementary, and
.
— 2. Jordan measure —
We now have a satisfactory notion of measure for elementary sets. But of course, the elementary sets are a very restrictive class of sets, far too small for most applications. For instance, a solid triangle or disk in the plane will not be elementary, or even a rotated box. On the other hand, as essentially observed long ago by Archimedes, such sets can be approximated from within and without by elementary sets
, and the inscribing elementary set
and the circumscribing elementary set
can be used to give lower and upper bounds on the putative measure of
. As one makes the approximating sets
increasingly fine, one can hope that these two bounds eventually match. This gives rise to the following definitions.
Definition 3 (Jordan measure) Let
be a bounded set.
- The inner Jordan measure
of
is defined as
- The outer Jordan measure
of
is defined as
- If
, then we say that
is Jordan measurable, and call
the Jordan measure of
. As before, we write
as
when we wish to emphasise the dimension
.
By convention, we do not consider unbounded sets to be Jordan measurable (they will be deemed to have infinite outer Jordan measure).
Jordan measurable sets are those sets which are “almost elementary” with respect to outer Jordan measure. More precisely, we have
Exercise 5 (Characterisation of Jordan measurability) Let
be bounded. Show that the following are equivalent:
is Jordan measurable.
- For every
, there exist elementary sets
such that
.
- For every
, there exists an elementary set
such that
.
As one corollary of this exercise, we see that every elementary set is Jordan measurable, and that Jordan measure and elementary measure coincide for such sets; this justifies the use of
to denote both. In particular, we still have
.
Jordan measurability also inherits many of the properties of elementary measure:
Exercise 6 Let
be Jordan measurable sets.
- (Boolean closure) Show that
,
,
, and
are Jordan measurable.
- (Non-negativity)
.
- (Finite additivity) If
are disjoint, then
.
- (Monotonicity) If
, then
.
- (Finite subadditivity)
.
- (Translation invariance) For any
,
is Jordan measurable, and
.
Now we give some examples of Jordan measurable sets:
Exercise 7 (Regions under graphs are Jordan measurable) Let
be a closed box in
, and let
be a continuous function.
- Show that the graph
is Jordan measurable in
with Jordan measure zero. (Hint: on a compact metric space, continuous functions are uniformly continuous.)
- Show that the set
is Jordan measurable.
Exercise 8 Let
be three points in
.
- Show that the solid triangle with vertices
is Jordan measurable.
- Show that the Jordan measure of the solid triangle is equal to
, where
.
(Hint: It may help to first do the case when one of the edges, say
, is horizontal.)
Exercise 9 Show that every compact convex polytope in
is Jordan measurable.
Exercise 10
- Show that all open and closed Euclidean balls
,
in
are Jordan measurable, with Jordan measure
for some constant
depending only on
.
- Establish the crude bounds
(An exact formula for
is
, where
is the volume of the unit sphere
and
is the Gamma function, but we will not derive this formula here.)
Exercise 11 Let
be a linear transformation.
- Show that there exists a non-negative real number
such that
for every elementary set
(note from previous exercises that
is Jordan measurable). Hint: apply Exercise 3 to the map
.
- Show that if
is Jordan measurable, then
is also, and
.
- Show that
. (Hint: Work first with the case when
is an elementary transformation, using Gaussian elimination. Alternatively, work with the cases when
is a diagonal transformation or an orthogonal transformation, using the unit ball in the latter case, and use the polar decomposition.)
Exercise 12 Define a Jordan null set to be a Jordan measurable set of Jordan measure zero. Show that any subset of a Jordan null set is a Jordan null set.
Exercise 13 Show that (1) holds for all Jordan measurable
.
Exercise 14 (Metric entropy formulation of Jordan measurability) Define a dyadic cube to be a half-open box of the form
for some integers
. Let
be a bounded set. For each integer
, let
denote the number of dyadic cubes of sidelength
that are contained in
, and let
be the number of dyadic cubes of sidelength
that intersect
. Show that
is Jordan measurable if and only if
in which case one has
Exercise 15 (Uniqueness of Jordan measure) Let
. Let
be a map from the collection
of Jordan-measurable subsets of
to the nonnegative reals that obeys the non-negativity, finite additivity, and translation invariance properties. Show that there exists a constant
such that
for all Jordan measurable sets
. In particular, if we impose the additional normalisation
, then
.
Exercise 16 Let
, and let
,
be Jordan measurable sets. Show that
is Jordan measurable, and
.
Exercise 17 Let
be two polytopes in
. Suppose that
can be partitioned into finitely many sub-polytopes which, after being rotated and translated, form a cover of
, with any two of the sub-polytopes in
intersecting only at their boundaries. Conclude that
and
have the same Jordan measure. The converse statement is true in one and two dimensions
(this is the Bolyai-Gerwien theorem), but false in higher dimensions (this was Dehn’s negative answer to Hilbert’s third problem).
The above exercises give a fairly large class of Jordan measurable sets. However, not every subset of is Jordan measurable. First of all, the unbounded sets are not Jordan measurable, by construction. But there are also bounded sets that are not Jordan measurable:
Exercise 18 Let
be a bounded set.
- Show that
and the closure
of
have the same outer Jordan measure.
- Show that
and the interior
of
have the same inner Jordan measure.
- Show that
is Jordan measurable if and only if the topological boundary
of
has outer Jordan measure zero.
- Show that the bullet-riddled square
, and set of bullets
, both have inner Jordan measure zero and outer Jordan measure one. In particular, both sets are not Jordan measurable.
Informally, any set with a lot of “holes”, or a very “fractal” boundary, is unlikely to be Jordan measurable. In order to measure such sets we will need to develop Lebesgue measure, which is done in the next set of notes.
Exercise 19 (Carathéodory type property) Let
be a bounded set, and
be an elementary set. Show that
.
— 3. Connection with the Riemann integral —
To conclude these notes we briefly discuss the relationship between Jordan measure and the Riemann integral (or the equivalent Darboux integral). For simplicity we will only discuss the classical one-dimensional Riemann integral on an interval , though one can extend the Riemann theory without much difficulty to higher-dimensional integrals on Jordan measurable sets. (In later notes, this Riemann integral will be superceded by the Lebesgue integral.)
Definition 4 (Riemann integrability) Let
be an interval of positive length, and
be a function. A tagged partition
of
is a finite sequence of real numbers
, together with additional numbers
for each
. We abbreviate
as
. The quantity
will be called the norm of the tagged partition. The Riemann sum
of
with respect to the tagged partition
is defined as
We say that
is Riemann integrable on
if there exists a real number, denoted
and referred to as the Riemann integral of
on
, for which we have
by which we mean that for every
there exists
such that
for every tagged partition
with
.
If
is an interval of zero length, we adopt the convention that every function
is Riemann integrable, with a Riemann integral of zero.
Note that unbounded functions cannot be Riemann integrable (why?).
The above definition, while geometrically natural, can be awkward to use in practice. A more convenient formulation of the Riemann integral can be formulated using some additional machinery.
Exercise 20 (Piecewise constant functions) Let
be an interval. A piecewise constant function
is a function for which there exists a partition of
into finitely many intervals
, such that
is equal to a constant
on each of the intervals
. If
is piecewise constant, show that the expression
is independent of the choice of partition used to demonstrate the piecewise constant nature of
. We will denote this quantity by
, and refer to it as the piecewise constant integral of
on
.
Exercise 21 (Basic properties of the piecewise constant integral) Let
be an interval, and let
be piecewise constant functions. Establish the following statements:
- (Linearity) For any real number
,
and
are piecewise constant, with
and
.
- (Monotonicity) If
pointwise (i.e.
for all
) then
.
- (Indicator) If
is an elementary subset of
, then the indicator function
(defined by setting
when
and
otherwise) is piecewise constant, and
.
Definition 5 (Darboux integral) Let
be an interval, and
be a bounded function. The lower Darboux integral
of
on
is defined as
where
ranges over all piecewise constant functions that are pointwise bounded above by
. (The hypothesis that
is bounded ensures that the supremum is over a non-empty set.) Similarly, we define the upper Darboux integral
of
on
by the formula
Clearly
. If these two quantities are equal, we say that
is Darboux integrable, and refer to this quantity as the Darboux integral of
on
.
Note that the upper and lower Darboux integrals are related by the reflection identity
Exercise 22 Let
be an interval, and
be a bounded function. Show that
is Riemann integrable if and only if it is Darboux integrable, in which case the Riemann integral and Darboux integrals are equal.
Exercise 23 Show that any continuous function
is Riemann integrable. More generally, show that any bounded, piecewise continuous function
is Riemann integrable.
Now we connect the Riemann integral to Jordan measure in two ways. First, we connect the Riemann integral to one-dimensional Jordan measure:
Exercise 24 (Basic properties of the Riemann integral) Let
be an interval, and let
be Riemann integrable. Establish the following statements:
- (Linearity) For any real number
,
and
are Riemann integrable, with
and
.
- (Monotonicity) If
pointwise (i.e.
for all
) then
.
- (Indicator) If
is a Jordan measurable subset of
, then the indicator function
(defined by setting
when
and
otherwise) is Riemann integrable, and
.
Finally, show that these properties uniquely define the Riemann integral, in the sense that the functional
is the only map from the space of Riemann integrable functions on
to
which obeys all three of the above properties.
Next, we connect the integral to two-dimensional Jordan measure:
Exercise 25 (Area interpretation of the Riemann integral) Let
be an interval, and let
be a bounded function. Show that
is Riemann integrable if and only if the sets
and
are both Jordan measurable in
, in which case one has
where
denotes two-dimensional Jordan measure. (Hint: First establish this in the case when
is non-negative.)
Exercise 26 Extend the definition of the Riemann and Darboux integrals to higher dimensions, in such a way that analogues of all the previous results hold.

83 comments
Comments feed for this article
3 February, 2022 at 9:13 pm
sin
Dear Professor Tao:
For (2) of exercise 8, can one simply match the definition of upper and lower Riemman integeral with those of jordan outer and inner measure respectively and conclude that the measure does coincide with the area ?
[Yes, this will work – T.]
9 February, 2022 at 9:07 pm
sin
Dear professor Tao:
For (3) of exercise 11, I’m struggling to show that if L is a shear, then the measure of the image of the unit box is 1. Since L does not map boxes to boxes as the other two types of elementary transformations do, how should one proceeds from here ?
[Upper and lower bound the sheared box by a union of finitely many boxes. You can draw some pictures in two dimensions first to get intuition. -T]
23 February, 2022 at 3:59 pm
sin
Dear professor Tao:
I greatly appreciate all the patient responses from you. In Definition 7.4,1 of your analysis 2, the splitting property is used to test Lebesgue measurability, I wonder if the Carathéodory type property can be used to test Jordan measurability in a similar fashion?
17 June, 2022 at 2:49 pm
Anonymous
Dr. Tao: be a closed box in
be a closed box in 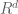 ,
, be a continuous function,
be a continuous function,
Let
and
consider the set
Someone mentioned that . i.e.
. i.e.  is just the graph of
is just the graph of  ? If that’s the case, then Exercise 7(2) follows easily from (1). But the boundary should also include the bottom box
? If that’s the case, then Exercise 7(2) follows easily from (1). But the boundary should also include the bottom box  , and the side surface set
, and the side surface set
 . The graph only covers the top of the set
. The graph only covers the top of the set  . Is this correct?
. Is this correct?
[Yes, but it is easy to manage the contribution of these additional regions for the purposes of establishing Exercise 7(2). -T]
4 March, 2024 at 4:38 pm
Anonymous
Dear professor Tao: Can you provide a bit hint on Exercise 9 (Jordan measurability of compact convex polytype)?
17 March, 2024 at 6:01 pm
Terence Tao
Try the case of a triangle in a plane first (perhaps assuming some of the sides parallel to the axes as an easier case), and then use the various Boolean algebra properties of Jordan measurability to handle other polygons. Then think about how to extend this argument to higher dimensions.