Peter Denton, Stephen Parke, Xining Zhang, and I have just uploaded to the arXiv a completely rewritten version of our previous paper, now titled “Eigenvectors from Eigenvalues: a survey of a basic identity in linear algebra“. This paper is now a survey of the various literature surrounding the following basic identity in linear algebra, which we propose to call the eigenvector-eigenvalue identity:
Theorem 1 (Eigenvector-eigenvalue identity) Let
be an
Hermitian matrix, with eigenvalues
. Let
be a unit eigenvector corresponding to the eigenvalue
, and let
be the
component of
. Then
where
is the
Hermitian matrix formed by deleting the
row and column from
.
When we posted the first version of this paper, we were unaware of previous appearances of this identity in the literature; a related identity had been used by Erdos-Schlein-Yau and by myself and Van Vu for applications to random matrix theory, but to our knowledge this specific identity appeared to be new. Even two months after our preprint first appeared on the arXiv in August, we had only learned of one other place in the literature where the identity showed up (by Forrester and Zhang, who also cite an earlier paper of Baryshnikov).
The situation changed rather dramatically with the publication of a popular science article in Quanta on this identity in November, which gave this result significantly more exposure. Within a few weeks we became informed (through private communication, online discussion, and exploration of the citation tree around the references we were alerted to) of over three dozen places where the identity, or some other closely related identity, had previously appeared in the literature, in such areas as numerical linear algebra, various aspects of graph theory (graph reconstruction, chemical graph theory, and walks on graphs), inverse eigenvalue problems, random matrix theory, and neutrino physics. As a consequence, we have decided to completely rewrite our article in order to collate this crowdsourced information, and survey the history of this identity, all the known proofs (we collect seven distinct ways to prove the identity (or generalisations thereof)), and all the applications of it that we are currently aware of. The citation graph of the literature that this ad hoc crowdsourcing effort produced is only very weakly connected, which we found surprising:

The earliest explicit appearance of the eigenvector-eigenvalue identity we are now aware of is in a 1966 paper of Thompson, although this paper is only cited (directly or indirectly) by a fraction of the known literature, and also there is a precursor identity of Löwner from 1934 that can be shown to imply the identity as a limiting case. At the end of the paper we speculate on some possible reasons why this identity only achieved a modest amount of recognition and dissemination prior to the November 2019 Quanta article.

40 comments
Comments feed for this article
3 December, 2019 at 7:34 pm
Anonymous
in page 9, remark 7, the name is Aram not Adam.
[Thanks, this will be corrected in the next revision of the ms. -T]
3 December, 2019 at 8:40 pm
kodlu
A commendable effort to bring all these related identities together.
3 December, 2019 at 8:44 pm
kodlu
Is there supposed to be an image (of a graph) after “The citation graph of the literature that this ad hoc crowdsourcing effort produced is only very weakly connected, which we found surprising:”
All that is visible in my browser is “???”
[Corrected, thanks – T.]
3 December, 2019 at 9:26 pm
Raphael
Really cool! Congratulations, I like that you mention chemical GT and the citation graph really rocks. I will consider something like that for my publications in similar cases (minireview by rediscovery) as well!
4 December, 2019 at 12:23 am
L
Do $PI$-algebras have application to this and vice versa?
4 December, 2019 at 2:42 am
Jochen Voss
The Karl Löwner (1934) references in the article on arXiv is shortened to LӞ4, which looks odd. Probably the surname should be spelled L{\”o}wner instead of L\”owner in bibtex?
[Thanks, this will be corrected in the next revision of the ms. -T]
4 December, 2019 at 6:02 am
3 GiftedNova
Is this an accidental calculation on how neutrinos change resulting in the formula or theorem describing the relationship between eigenvectors and eigenvalues
4 December, 2019 at 6:47 am
Mark Meckes
This is truly a service to the scientific community. Linear algebra, being as it is central to an extremely broad swath of fields of pure and applied mathematics, seems especially prone to this sort of independent rediscovery of useful facts that lie just a bit beyond the level of introductory textbooks. I wasn’t at all surprised by the tree-like nature of the citation graph.
Although it’s not quite the same phenomenon, I was reminded of a talk I heard Barry Simon give (see e.g. here) on a widely unnoticed proof of the main result from the same paper of Löwner that you mentioned.
4 December, 2019 at 1:18 pm
Anonymous
Another example is Heegner’s solution (from 1952) of the class number 1 problem (which unfortunately remained unnoticed for more a decade)
4 December, 2019 at 7:28 am
[Terence Tao's blog] Eigenvectors from Eigenvalues: a survey of a basic identity in linear algebra - Nevin Manimala's Blog
[…] by /u/Valvino [link] […]
4 December, 2019 at 7:58 am
Andrew Krause
I especially enjoyed the sociology of science of all of this. I constantly feel that there must be better ways to organize the enormous enterprise that is research mathematics, but any such organization will undoubtedly have flaws.
A few typos involving repeated words in the preprint: “for for” appears at the end of Section 5, and “the the” at the end of Section 4.
[Thanks, this will be corrected in the next revision of the ms. -T]
4 December, 2019 at 8:57 am
liuyao
A small complaint: the formula is only useful when lambda_i is simple (or else both sides vanish, by Cauchy interlacing), so why not just write it in quotient form? (The only argument may be that the identity does not rely on Cauchy interlacing.)
Also, what is the current state for “fingerprint databases for mathematical theorems”? The paper [BT13] dates from 2013, and one could at least add https://www.lmfdb.org/ to the list.
Not entirely the same, but getting the *statements* in (one agreed-on) proof assistant could be an important step: https://formalabstracts.github.io/
4 December, 2019 at 9:31 am
Terence Tao
The non-quotiented form has the advantage of being valid for all diagonalizable matrices taking values in an arbitrary commutative ring (not just real or complex numbers), as it avoids any requirement of invertibility of any of the quantities involved. (For this generalization one needs to distinguish the left eigenvectors from the right eigenvectors, see equation (11) in the new version of the paper.) There are also variants of the identity that are non-degenerate in the case of multiple eigenvalues; see for instance (15) of the new version of the paper.
The non-quotiented form also has a slightly non-trivial corollary: if lies in the spectrum of
lies in the spectrum of  , then either
, then either 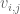 vanishes or
vanishes or  is a repeated eigenvalue. I don’t know of a short direct way to see this implication (although the converse implications are not difficult, see consistency checks (iv), (v) in the new version of the paper).
is a repeated eigenvalue. I don’t know of a short direct way to see this implication (although the converse implications are not difficult, see consistency checks (iv), (v) in the new version of the paper).
Unfortunately I do not know of any followup work to [BT13], but perhaps there are other readers of this blog who may be aware of more recent developments in this area.
4 December, 2019 at 2:49 pm
Kristoffer Varholm
There is a typo on the first line of page 7. Eigenvectors should be eigen_values_.
[Thanks, this will be corrected in the next revision of the ms – T.]
4 December, 2019 at 3:44 pm
arch1
Typo, penultimate sentence: “…we are not able to guarantee that there is *not* an even earlier reference in the literature…”
[Thanks, this will be corrected in the next revision of the ms – T.]
4 December, 2019 at 4:07 pm
Max
The meaning of $\lambda_k(M_j)$ seems quite obscure to me. For a matrix $B = M_j$ different from A, $\lambda_k(B)$ is just any of the eigenvalues of B (and in addition you have a different B for each j). These are a priori totally unrelated with the { \lambda_k(A) }, even the range of the indices is not the same since the size of B is not that of A.
4 December, 2019 at 4:18 pm
Max
Oops, sorry, please ignore the comment, I now understand that the product is taken over all n-1 eigenvalues of M_j, so it does not matter in which order they are taken. (Yet \lambda_k(M_j) is still ill defined /per se/ and a notation like $\prod_{\mu \in \spec M_j} …$ would IMHO be less confusing.)
6 December, 2019 at 6:28 am
Anonymous
Dear Pro.Tao,
We always trust your ability in solving a famous problem which was 3 centuries ago. Nearly end the year. Super speed! Come on! Only Sir understands our crazy comments! Sweet fruits are waiting for you after you spend a lot of time care , water, fertilizer your lovely tree.
6 December, 2019 at 4:19 pm
Alex Jones
Terry, with all due respect, may I ask why you were an author on the previous paper? I feel like there is a big “P vs NP” phenomenon going on with this identity. I think the big achievement (I’m tempted to say the “sole achievement”) is *finding* the identity rather than proving it once provided. I think you should have been thanked in the acknowledgments section rather than have been a coauthor.
7 December, 2019 at 8:02 am
Terence Tao
There are two previous papers, listed as [DPZ19] and [DPTZ19] in the references to the current version. [DPZ19] is where the identity was (once again) discovered but not proven; I am not an author of that paper. The now-superseded preprint [DPTZ19] consists of little more than two proofs of the identity, which I provided. (One of these proofs we now know to have been discovered multiple times already in the literature, but the other proof appears to be new.)
The four of us did discuss whether to instead add an appendix to [DPZ19] containing at least one of the proofs, but eventually decided on a standalone preprint to draw attention on the identity outside of the neutrino physics community. Needless to say this goal was achieved to a somewhat greater extent than we expected.
7 December, 2019 at 1:58 pm
Stephen Parke
As P of [DPZ19] and [DPTZ19], I fully concur with TT response to this comment.
6 December, 2019 at 10:00 pm
Anonymous
By n-1 th symmetric function you probably meant the n-1 th elementary symmetric function on page 4.
[Thanks, this will be corrected in the next revision of the ms. -T]
7 December, 2019 at 11:49 pm
aquazorcarson
Also the summation is perhaps a product on the next line. Nice observation by the way.
[Thanks, this will be corrected in the next revision of the ms. -T]
6 December, 2019 at 10:13 pm
Darij Grinberg
Kudos for doing the thankless literature review work everyone has been shying away from. Everyone knows the linear algebra literature is self-similar like a fractal, but actually playing the memory game is not something people usually find the stomach for.
A trivial typo: “Sbastien” -> “Sébastien” in [GKV]. This is likely a mojibake issue in your bibliography.
Anyway, here is another proof of the result, which I believe to be more general than the ones in the paper, as it uses neither the base field being a field (let alone the complex numbers), nor diagonalization (only an eigenvector of and one of
and one of 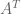 ), nor any sort of normality. (Feel free to include it!)
), nor any sort of normality. (Feel free to include it!)
Here is the general form that I’ll be proving:
=== BEGIN THEOREM ===
THEOREM 1: Let be a commutative ring. Let
be a commutative ring. Let  be an
be an  -by-
-by- -matrix over
-matrix over  . Let
. Let  . Let
. Let 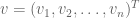 and
and 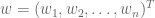 be two column vectors in
be two column vectors in 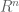 such that
such that 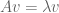 and
and  . Fix
. Fix 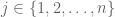 , and let M_j be the
, and let M_j be the 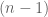 -by-
-by-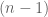 -matrix obtained from
-matrix obtained from  by removing row
by removing row  and column
and column  . Then,
. Then,
Here, denotes the characteristic polynomial of a matrix
denotes the characteristic polynomial of a matrix  .
.
=== END THEOREM ===
This is probably closest to the equality (4) in arXiv:1908.03795v2, but the use of and
and 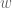 (as opposed to a single
(as opposed to a single  ) is from Remark 4. The eigenvectors
) is from Remark 4. The eigenvectors  and
and 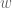 are not connected to each other apart from corresponding to the same eigenvalue; but there is a fudge factor
are not connected to each other apart from corresponding to the same eigenvalue; but there is a fudge factor  on the right hand side that ensures homogeneity of the equality.
on the right hand side that ensures homogeneity of the equality.
The first step to proving Theorem 1 is to simplify it a lot by replacing by
by 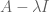 . (Not my idea; you do the same in the last paragraph of §2.5.) Thus, Theorem 1 reduces to the following simpler fact:
. (Not my idea; you do the same in the last paragraph of §2.5.) Thus, Theorem 1 reduces to the following simpler fact:
=== BEGIN THEOREM ===
THEOREM 2: Let be a commutative ring. Let
be a commutative ring. Let  be an
be an  -by-
-by- -matrix over
-matrix over  . Let
. Let 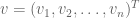 and
and 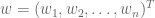 be two column vectors in
be two column vectors in 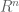 such that
such that 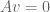 and
and 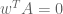 . Fix
. Fix 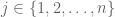 . For each
. For each 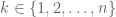 , let
, let  be the
be the 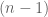 -by-
-by-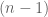 -matrix obtained from
-matrix obtained from  by removing row
by removing row  and column
and column  . Then,
. Then,
=== END THEOREM ===
This is what Theorem 1 boils down to after replacing by
by 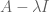 , because
, because 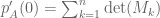 .
.
Here is the first lemma that we will use to prove this:
=== BEGIN LEMMA ===
LEMMA 3: Let be a commutative ring. Let
be a commutative ring. Let  be an
be an  -by-
-by- -matrix over
-matrix over  . Let
. Let 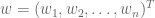 be a column vector in
be a column vector in 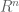 such that
such that 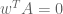 . Fix
. Fix 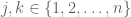 . Then,
. Then,
for every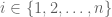 .
.
=== END LEMMA ===
Here, denotes the
denotes the 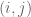 -th entry of a matrix
-th entry of a matrix  .
.
PROOF OF LEMMA 3: Let be the
be the  -by-
-by- matrix obtained from
matrix obtained from  by multiplying the
by multiplying the  -th row by
-th row by 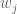 and multiplying the
and multiplying the  -th row by
-th row by 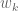 . It is thus easy to see that
. It is thus easy to see that
and
Hence, it remains to prove that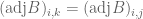 .
.
But we assumed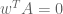 , so that
, so that
Thus,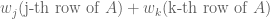 is a linear combination of the remaining rows of
is a linear combination of the remaining rows of  . In view of how
. In view of how  was defined, we can rewrite this as follows:
was defined, we can rewrite this as follows:  is a linear combination of the remaining rows of
is a linear combination of the remaining rows of  . From this, it is easy to derive that
. From this, it is easy to derive that  by simple row operations (indeed, the matrix whose determinant is
by simple row operations (indeed, the matrix whose determinant is 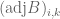 is obtained from the matrix whose determinant is
is obtained from the matrix whose determinant is 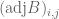 by some simple row operations). Lemma 3 is proved (not as neatly as I hoped for, but I suspect you can simplify the argument).
by some simple row operations). Lemma 3 is proved (not as neatly as I hoped for, but I suspect you can simplify the argument).
Here is a column analogue of Lemma 3:
=== BEGIN LEMMA ===
LEMMA 4: Let be a commutative ring. Let
be a commutative ring. Let  be an
be an  -by-
-by- -matrix over
-matrix over  . Let
. Let 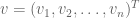 be a column vector in
be a column vector in 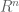 such that
such that 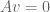 . Fix
. Fix 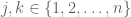 . Then,
. Then,
=== END LEMMA ===
PROOF OF LEMMA 4: Analogous to Lemma 3. (Or, even easier, just apply Lemma 3 to A^T instead of A.)
Combining Lemma 3 with Lemma 4 quickly yields the following:
=== BEGIN COROLLARY ===
COROLLARY 5: Let be a commutative ring. Let
be a commutative ring. Let  be an
be an  -by-
-by- -matrix over
-matrix over  . Let
. Let 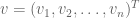 and
and 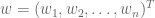 be two column vectors in
be two column vectors in 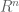 such that
such that 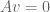 and
and 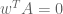 . Fix
. Fix 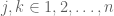 . Then,
. Then,
(with notations and
and  as in Theorem 2).
as in Theorem 2).
=== END COROLLARY ===
PROOF OF COROLLARY 5: Lemma 3 (applied to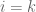 ) yields
) yields
Lemma 4 (applied to ) yields
) yields
Multiplying the first of these two equalities by and the second by
and the second by 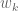 , we obtain
, we obtain
In view of and
and 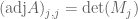 , we see that we have obtained precisely the claim of Corollary 5.
, we see that we have obtained precisely the claim of Corollary 5.
PROOF OF THEOREM 2: We have
This proves Theorem 2.
[Thanks, we will mention this in the next revision of the ms -T.]
19 December, 2019 at 9:59 am
Darij Grinberg
The handwavy nature of my proof of Lemma 3 in the parent comment kept ruffling my feathers, so here is an alternative proof.
SECOND PROOF OF LEMMA 3. WLOG assume that , since otherwise the claim is obvious. Let
, since otherwise the claim is obvious. Let  be the column vector in
be the column vector in  whose
whose 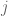 -th entry is
-th entry is 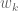 , whose
, whose  -th entry is
-th entry is 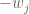 , and whose all remaining entries are
, and whose all remaining entries are  . Then, the claim of Lemma 3 is easily seen to be equivalent to the matrix equality
. Then, the claim of Lemma 3 is easily seen to be equivalent to the matrix equality  .
.
At this point, I want to recall a known fact, but as usual the only place where I remember it from is my own writeup (Theorem 5.14 in https://www.cip.ifi.lmu.de/~grinberg/algebra/trach.pdf ): The adjugate of a square matrix can be written as a polynomial in said matrix. Applying this to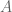 , we conclude that
, we conclude that  can be written as a polynomial in
can be written as a polynomial in 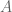 . Hence, in order to prove that
. Hence, in order to prove that  , it suffices to show that
, it suffices to show that 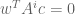 for each nonnegative integer
for each nonnegative integer 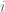 . But this is easy: For
. But this is easy: For 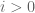 , this follows from
, this follows from 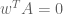 , but for
, but for  , this follows from
, this follows from 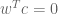 (which is checked by direct verification). And Lemma 3 is proved again.
(which is checked by direct verification). And Lemma 3 is proved again.
27 December, 2019 at 1:57 am
Darij Grinberg
PS (or PPS). The “known fact” I used in the second proof of Lemma 3 above has a MathOverflow thread devoted to it: https://mathoverflow.net/questions/32133/expressing-adja-as-a-polynomial-in-a
19 February, 2021 at 5:32 am
Darij Grinberg
The “second proof of Lemma 3” I gave above is wrong. Sorry! (Thanks Ion Zaballa for spotting the error.)
8 December, 2019 at 7:35 am
Zubereitung Inhalt
Dear Professor Tao:
I am the guy who pointed out Löwner’s paper on Quanta. The version as stated by Löwner is very useful — see pp. 224–226 in Demmel’s Applied Numerical Linear Algebra. Your version, on the other hand, is just a consequence of the fact (see Wikipedia) that if an matrix
matrix  has rank
has rank 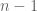 , then
, then  has rank
has rank  and
and 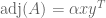 where
where 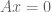 ,
, 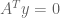 . Apply this to
. Apply this to 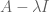 for a simple eigenvalue
for a simple eigenvalue  and left/right eigenvectors
and left/right eigenvectors  and
and  .
.
8 December, 2019 at 10:59 am
Zubereitung Inhalt
Dear Professor Terry:
Do you think something like a LaTeX-aware search engine for math papers would be a good idea in these kinds of situations? Also do you think that there should be an effort to revive tricki.org?
16 November, 2023 at 5:10 pm
Anonymous
A physics major mentioned to me a couple of years ago the difficulty of googling math results and equations and asked me how to work around it. I never got back to look at it.
8 December, 2019 at 1:11 pm
Michael Ruxton
https://www.irishtimes.com/news/science/particle-physics-gives-maths-potentially-powerful-new-tool-1.4095391
9 December, 2019 at 7:15 pm
Margaret Stawiska-Friedland
The argument I posted on November 23, 2019 as a comment under the previous post on eigenvectors from eigenvalues can be made to work for multiple eigenvalues, at least for matrices over the field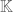 of either real of complex numbers.
of either real of complex numbers. be an
be an  matrix over
matrix over 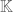 . Let
. Let 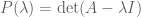 be the characteristic polynomial of
be the characteristic polynomial of  .
.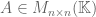 corresponding to an eigenvalue
corresponding to an eigenvalue  with geometric multiplicity
with geometric multiplicity 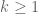 we get the following expressions, provided that the algebraic multiplicity also equals
we get the following expressions, provided that the algebraic multiplicity also equals  : Let
: Let  be a basis of eigenvectors corresponding to
be a basis of eigenvectors corresponding to  . Let
. Let  be a basis of eigenvectors of
be a basis of eigenvectors of 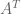 such that
such that  (here we use the assumption on algebraic multiplicity also being
(here we use the assumption on algebraic multiplicity also being  ). Let
). Let  and
and  . Then
. Then 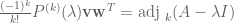 .
.
Let
For eigenvectors of
This is a matrix equality; I do not attempt to rewrite it entrywise.
Proof: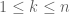 the
the  -th adjugate of
-th adjugate of  , denoted by
, denoted by  , is defined as follows:
, is defined as follows: is
is  times the
times the 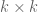 -minor of
-minor of  obtained by deleting the rows
obtained by deleting the rows 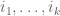 and columns
and columns  . Note that the usual adjugate
. Note that the usual adjugate  is
is 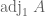 . We will also use
. We will also use -th compound matrix
-th compound matrix 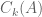 , which is the matrix in
, which is the matrix in  whose entries are the
whose entries are the 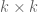 minors of
minors of  arranged in the lexicographical order. (If
arranged in the lexicographical order. (If  represents a linear transformation
represents a linear transformation 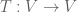 , then
, then 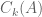 represents
represents  in suitable bases.) . It is straightforward to show that that
in suitable bases.) . It is straightforward to show that that 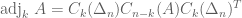 , where
, where  is the matrix whose
is the matrix whose  entry is
entry is  .
.
For
The entry
the
The Laplace expansion along minors implies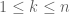 ):
):
the following identities (
From the identity it follows that
it follows that  if
if 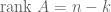 . Hence, if the nullity of
. Hence, if the nullity of 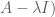 is
is  , we can represent
, we can represent  as
as 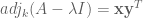 , where
, where 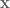 and
and 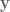 are vectors in
are vectors in  . From the relation between the compound and adjugate matrix it follows that
. From the relation between the compound and adjugate matrix it follows that 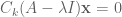 and
and  . Let now
. Let now 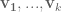 be a basis of eigenvectors for
be a basis of eigenvectors for  . Then
. Then  is an eigenvector for
is an eigenvector for 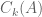 corresponding to the eigenvalue $\lambda^k$, which has geometric multiplicity
corresponding to the eigenvalue $\lambda^k$, which has geometric multiplicity  .
. as a basis for
as a basis for  , so
, so 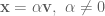 . Let
. Let  . Then
. Then 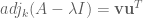 . If the algebraic multiplicity of $\lambda$ as the eigenvalue of
. If the algebraic multiplicity of $\lambda$ as the eigenvalue of  is also
is also  , there exist
, there exist  such that
such that  Taking
Taking  we get
we get 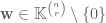 such that
such that 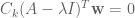 ,
, 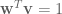 . We then have
. We then have 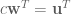
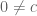 and
and 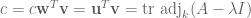 . Hence
. Hence  .
.
We can take
with
We can replace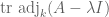 by the suitably scaled
by the suitably scaled  -th derivative of
-th derivative of  evaluated at
evaluated at  thanks to the following formula: for
thanks to the following formula: for  arbitrary matrices in
arbitrary matrices in  ,
, 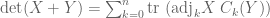 , proved as Theorem 4.1 in: Prells, Uwe; Friswell, Michael I.; Garvey, Seamus D. (2003-02-08). “Use of geometric algebra: compound matrices and the determinant of the sum of two matrices''. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 459 (2003): 273-285. For the purpose of finding the appropriate differential expression, the formula is applied to the matrices
, proved as Theorem 4.1 in: Prells, Uwe; Friswell, Michael I.; Garvey, Seamus D. (2003-02-08). “Use of geometric algebra: compound matrices and the determinant of the sum of two matrices''. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 459 (2003): 273-285. For the purpose of finding the appropriate differential expression, the formula is applied to the matrices 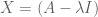 and
and  , and then we take
, and then we take 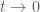 in
in 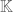 (polynomials are identified with polynomial functions, which are smooth).
(polynomials are identified with polynomial functions, which are smooth).
The assumption of the algebraic multiplicity of the eigenvalue being equal to its geometric multiplicity can be justified by the following easy result:
Let be an
be an  -dimensional vector space over
-dimensional vector space over 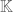 and let
and let 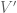 be its dual space. Let
be its dual space. Let 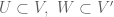 be two
be two  -dimensional subspaces. TFAE: (i)
-dimensional subspaces. TFAE: (i) 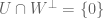 ; (ii)
; (ii) 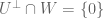 ; (iii) There exist bases
; (iii) There exist bases  ,
,  in
in  and
and  , respectively, such that
, respectively, such that  .
.
11 December, 2019 at 5:57 pm
Some Light Winter Break Mathematical Reading – Advice and Resources for Math Graduate Students
[…] be described by a formula involving only the eigenvalues of the matrix and certain submatrices. Tao’s blog has a concise description of the precise statement. Their preprint is worth a look too: after […]
11 December, 2019 at 6:06 pm
Some light winter break math reading – Advice and Resources for Math Graduate Students
[…] described by a formula involving only the eigenvalues of the matrix and certain submatrices. See Tao’s blog for a concise description of the precise statement. Their preprint is worth a look too: after […]
13 December, 2019 at 4:36 pm
Edward Zeng
Dear Professor Tao,
I’m a sophomore math major at Berkeley. Someone told me about this theorem, and I think I found another proof.
Set . WLOG assume
. WLOG assume  . Then the formula to be proved is
. Then the formula to be proved is

First we note any Hermitian matrix can be diagonalized by a unitary transformation
can be diagonalized by a unitary transformation

 form a basis of unit eigenvectors,
form a basis of unit eigenvectors,

where the column vectors of
Now observe the following lemma, which follows directly from how determinants are computed.
Lemma 1: Let
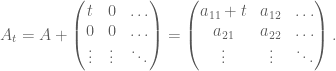 Then
Then  .
.
Applying T-transformation to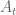 , we obtain
, we obtain

When we take the determinant on both sides (using Lemma 1 on the LHS) and collect the t-linear terms, we obtain the desired formula.
14 January, 2020 at 3:22 pm
Milad Kiaee Darunkola
This is related to the problem of Stars and Bars in Combinatorics.
20 February, 2020 at 11:15 pm
Cole Green
Our research group simulates photosynthetic nanotubules in Green Sulphur Bacteria. To study systems comparable in size to those found in nature, we must calculate the eigenvectors of large hamiltonians (up to 10,000×10,000). We do this by using LLAPACK’s DSYEV package, but this takes a long time for large systems. Since we only require the magnitude of the eigenvectors’ components for many of our calculations, we tested whether this new method for finding eigenvectors could be implemented in order to create faster programs. We found that this method was considerably slower than DSYEV, but we would like to improve the program if possible. Has anyone attempted something similar to this?
If you would like more information about the results of our comparison or have any suggestions, please contact me at cdgreen@my.loyno.edu or reply to this post
26 February, 2020 at 1:23 am
יומיות 29.12.2019: WT.social, רשת חברתית חדשה למקים ויקיפדיה | ניימן 3.0
[…] זמן קצר הם גילו שהם לא הראשונים שגילו את הזהות, אלא הראשונים שנתנו לה מסגרת וחשיבות משלה. מהר מאד הם […]
21 May, 2020 at 7:22 am
Sylvain Ribault
One way to avoid having to rediscover the wheel too often: write such results more systematically in Wikipedia.
3 June, 2020 at 7:31 am
Server Bug Fix: How do you check that your mathematical research topic is original? - TECHPRPR
[…] is one that is relevant to all mathematicians. An interesting recent example that comes to mind is this story on Terence Tao’s […]