Van Vu and I have just uploaded to the arXiv our paper “Random matrices: Universality of eigenvectors“, submitted to Random Matrices: Theory and Applications. This paper concerns an extension of our four moment theorem for eigenvalues. Roughly speaking, that four moment theorem asserts (under mild decay conditions on the coefficients of the random matrix) that the fine-scale structure of individual eigenvalues of a Wigner random matrix depend only on the first four moments of each of the entries.
In this paper, we extend this result from eigenvalues to eigenvectors, and specifically to the coefficients of, say, the eigenvector
of a Wigner random matrix
. Roughly speaking, the main result is that the distribution of these coefficients also only depends on the first four moments of each of the entries. In particular, as the distribution of coefficients eigenvectors of invariant ensembles such as GOE or GUE are known to be asymptotically gaussian real (in the GOE case) or gaussian complex (in the GUE case), the same asymptotic automatically holds for Wigner matrices whose coefficients match GOE or GUE to fourth order.
(A technical point here: strictly speaking, the eigenvectors are only determined up to a phase, even when the eigenvalues are simple. So, to phrase the question properly, one has to perform some sort of normalisation, for instance by working with the coefficients of the spectral projection operators
instead of the eigenvectors, or rotating each eigenvector by a random phase, or by fixing the first component of each eigenvector to be positive real. This is a fairly minor technical issue here, though, and will not be discussed further.)
This theorem strengthens a four moment theorem for eigenvectors recently established by Knowles and Yin (by a somewhat different method), in that the hypotheses are weaker (no level repulsion assumption is required, and the matrix entries only need to obey a finite moment condition rather than an exponential decay condition), and a slightly stronger conclusion (less regularity is needed on the test function, and one can handle the joint distribution of polynomially many coefficients, rather than boundedly many coefficients). On the other hand, the Knowles-Yin paper can also handle generalised Wigner ensembles in which the variances of the entries are allowed to fluctuate somewhat.
The method used here is a variation of that in our original paper (incorporating the subsequent improvements to extend the four moment theorem from the bulk to the edge, and to replace exponential decay by a finite moment condition). That method was ultimately based on the observation that if one swapped a single entry (and its adjoint) in a Wigner random matrix, then an individual eigenvalue would not fluctuate much as a consequence (as long as one had already truncated away the event of an unexpectedly small eigenvalue gap). The same analysis shows that the projection matrices
obeys the same stability property.
As an application of the eigenvalue four moment theorem, we establish a four moment theorem for the coefficients of resolvent matrices , even when
is on the real axis (though in that case we need to make a level repulsion hypothesis, which has been already verified in many important special cases and is likely to be true in general). This improves on an earlier four moment theorem for resolvents of Erdos, Yau, and Yin, which required
to stay some distance away from the real axis (specifically, that
for some small
).

12 comments
Comments feed for this article
29 March, 2011 at 4:17 am
Florent Benaych-Georges
Dear Professor Tao,
I have a question about your paper : I do not see what argument you use, in the beginning of the proof of Th. 17 page 16, when you say that Condition C1 allows to troncate to the case when the entries have size O(n^{10/C_0}) and that one can perturb the entries to make them continuous.
Yours,
Florent Benaych-Georges
29 March, 2011 at 8:35 am
Terence Tao
By Condition C1 and Chebyshev’s inequality, each matrix entry will be at most in magnitude with probability
in magnitude with probability  , and so by the union, all the entries of this matrix will have this property with probability
, and so by the union, all the entries of this matrix will have this property with probability  . So we may truncate the atom distribution to the
. So we may truncate the atom distribution to the 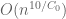 regime with an error of only
regime with an error of only  in the final expectation. (There is a minor technical issue that this truncation changes the first four moments of this distribution very slightly (by
in the final expectation. (There is a minor technical issue that this truncation changes the first four moments of this distribution very slightly (by 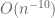 or so), but one can perturb the atom distribution slightly to correct for this, using the Weyl inequalities to measure the error which will be something like
or so), but one can perturb the atom distribution slightly to correct for this, using the Weyl inequalities to measure the error which will be something like  (say), which is still acceptable.)
(say), which is still acceptable.)
Similarly, if one has a discrete atom distribution, one can perturb it (e.g. by adding a small multiple of a gaussian) to obtain a new distribution that is continuous and has essentially the same first four moments (up to an arbitrarily small error). Again, one can use the Weyl inequalities to control the error (in fact, just a qualitative continuity argument would work in this case).
(These are examples of the more general “create an epsilon of room” argument: http://www.tricki.org/article/Create_an_epsilon_of_room )
29 March, 2011 at 10:04 pm
Florent Benaych-Georges
Drag Professor Tao,
Thanks a lot for your answer.
However, I do not see which inequality allows to control the eigenvectors of the Wigner matrix by the ones of the perturbed one.
Would you please indicate it to me?
Yours,
fbg
29 March, 2011 at 10:24 pm
Florent Benaych-Georges
In m’y previous message: “drag” –> “dear”.
Misprint!
30 March, 2011 at 7:42 am
Terence Tao
Ah, right, one is dealing with eigenvectors here as well as eigenvalues. But one could use for instance Lemma 22 in the paper (noting that one is already truncated to the region where there is an eigenvalue gap) to provide a suitable bound for the error in the perturbation (with plenty of powers of n to spare). Alternatively, one could weaken the hypotheses of the four moment theorem a little by allowing each of the four moments to vary by, say, O(n^{-10}), rather than match exactly, in which case one can truncate without needing to adjust the atom distributions outside of an event of small probability. (One still needs an adjustment to make the distributions continuous, but this is a qualitative adjustment that requires no quantitative bounds, and the qualitative Lemma 21 would suffice here.) We’ll add a note to the text to clarify this point.
30 March, 2011 at 10:16 am
Florent Benaych-Georges
Dear Professor Tao,
Thanks a lot for your answer.
In fact, what I am looking for (under possible additional hypotheses) is a rate of convergence for the convergence stated in Equation (2) of your paper (page 6).
To get it, I would need a result stating that for any finite set I of {1,..,n} (possibly depending on n, but with fixed cardinality), the eigenvalues with index in I (say, for example, the first, the fourth and the sixth eigenvalues) all have multiplicity one with overwhelming probability (whereas I only found results stating this with high probability).
I would rather say that this assertion is true, but I do not know where I could find it.
Do you know if such a result exists ?
Yours,
Florent Benaych-Georges
30 March, 2011 at 10:58 am
Terence Tao
This type of bound (overwhelming probability that eigenvalues are simple) is not yet in the literature, though Van and I are working on such a bound and hope to be able to have some results to announce in this direction soon. There are good repulsion estimates from a fixed energy E (i.e. the probability that some eigenvalue lambda_i is equal or very close to E can be bounded well), for instance by Erdos, Schlein, and Yau (under some smoothness hypotheses on the entries) and also recently by
RudelsonVershynin (in the model case E=0) but this is not quite the same as getting estimates for simplicity of eigenvalues (though it may be enough to get good bounds on the event that eigenvalue multiplicity exceeds, say, three).31 March, 2011 at 12:54 am
Florent Benaych-Georges
Thanks a lot for your answer. I’m looking forward to read your new results in this direction.
1 April, 2011 at 1:38 am
Florent Benaych-Georges
Dear Professor Tao,
I have another question : why do we have to suppose that m<=10 in Lemma 24 ? Could the number 10 be replaced by any fixed upper bound ?
Yours,
fbg
1 April, 2011 at 8:39 am
Terence Tao
Yes, any fixed m (which is at least 5) will work for the purposes of the four moment theorem.
2 April, 2011 at 5:29 am
Vu ha Van
Actually, Rudelson should be Vershynin. [Gah! Corrected, thanks – T.]
8 April, 2011 at 2:39 am
Florent Benaych-Georges
Dear Professor Tao,
I have uploaded to the arXiv a paper called “Eigenvectors of Wigner matrices: universality of global fluctuations” ( http://arxiv.org/abs/1104.1219 ), where I give a kind of (weak) global version of the “eigenvectors part” of your result. In this paper, I use some of the estimates you prove in your paper, especially Equation (27) of your Lemma 24, a bound I had been looking for for a while.
Yours,
Florent Benaych-Georges