Suppose one has a measure space and a sequence of operators
that are bounded on some
space, with
. Suppose that on some dense subclass of functions
in
(e.g. continuous compactly supported functions, if the space
is reasonable), one already knows that
converges pointwise almost everywhere to some limit
, for another bounded operator
(e.g.
could be the identity operator). What additional ingredient does one need to pass to the limit and conclude that
converges almost everywhere to
for all
in
(and not just for
in a dense subclass)?
One standard way to proceed here is to study the maximal operator
and aim to establish a weak-type maximal inequality
for all (or all
in the dense subclass), and some constant
, where
is the weak
norm
A standard approximation argument using (1) then shows that will now indeed converge to
pointwise almost everywhere for all
in
, and not just in the dense subclass. See for instance these lecture notes of mine, in which this method is used to deduce the Lebesgue differentiation theorem from the Hardy-Littlewood maximal inequality. This is by now a very standard approach to establishing pointwise almost everywhere convergence theorems, but it is natural to ask whether it is strictly necessary. In particular, is it possible to have a pointwise convergence result
without being able to obtain a weak-type maximal inequality of the form (1)?
In the case of norm convergence (in which one asks for to converge to
in the
norm, rather than in the pointwise almost everywhere sense), the answer is no, thanks to the uniform boundedness principle, which among other things shows that norm convergence is only possible if one has the uniform bound
for some and all
; and conversely, if one has the uniform bound, and one has already established norm convergence of
to
on a dense subclass of
, (2) will extend that norm convergence to all of
.
Returning to pointwise almost everywhere convergence, the answer in general is “yes”. Consider for instance the rank one operators
from to
. It is clear that
converges pointwise almost everywhere to zero as
for any
, and the operators
are uniformly bounded on
, but the maximal function
does not obey (1). One can modify this example in a number of ways to defeat almost any reasonable conjecture that something like (1) should be necessary for pointwise almost everywhere convergence.
In spite of this, a remarkable observation of Stein, now known as Stein’s maximal principle, asserts that the maximal inequality is necessary to prove pointwise almost everywhere convergence, if one is working on a compact group and the operators are translation invariant, and if the exponent
is at most
:
Theorem 1 (Stein maximal principle) Let
be a compact group, let
be a homogeneous space of
with a finite Haar measure
, let
, and let
be a sequence of bounded linear operators commuting with translations, such that
converges pointwise almost everywhere for each
. Then (1) holds.
This is not quite the most general vesion of the principle; some additional variants and generalisations are given in the original paper of Stein. For instance, one can replace the discrete sequence of operators with a continuous sequence
without much difficulty. As a typical application of this principle, we see that Carleson’s celebrated theorem that the partial Fourier series
of an
function
converge almost everywhere is in fact equivalent to the estimate
And unsurprisingly, most of the proofs of this (difficult) theorem have proceeded by first establishing (3), and Stein’s maximal principle strongly suggests that this is the optimal way to try to prove this theorem.
On the other hand, the theorem does fail for , and almost everywhere convergence results in
for
can be proven by other methods than weak
estimates. For instance, the convergence of Bochner-Riesz multipliers in
for any
(and for
in the range predicted by the Bochner-Riesz conjecture) was verified for
by Carbery, Rubio de Francia, and Vega, despite the fact that the weak
of even a single Bochner-Riesz multiplier, let alone the maximal function, has still not been completely verified in this range. (Carbery, Rubio de Francia and Vega use weighted
estimates for the maximal Bochner-Riesz operator, rather than
type estimates.) For
, though, Stein’s principle (after localising to a torus) does apply, though, and pointwise almost everywhere convergence of Bochner-Riesz means is equivalent to the weak
estimate (1).
Stein’s principle is restricted to compact groups (such as the torus or the rotation group
) and their homogeneous spaces (such as the torus
again, or the sphere
). As stated, the principle fails in the noncompact setting; for instance, in
, the convolution operators
are such that
converges pointwise almost everywhere to zero for every
, but the maximal function is not of weak-type
. However, in many applications on non-compact domains, the
are “localised” enough that one can transfer from a non-compact setting to a compact setting and then apply Stein’s principle. For instance, Carleson’s theorem on the real line
is equivalent to Carleson’s theorem on the circle
(due to the localisation of the Dirichlet kernels), which as discussed before is equivalent to the estimate (3) on the circle, which by a scaling argument is equivalent to the analogous estimate on the real line
.
Stein’s argument from his 1961 paper can be viewed nowadays as an application of the probabilistic method; starting with a sequence of increasingly bad counterexamples to the maximal inequality (1), one randomly combines them together to create a single “infinitely bad” counterexample. To make this idea work, Stein employs two basic ideas:
- The random rotations (or random translations) trick. Given a subset
of
of small but positive measure, one can randomly select about
translates
of
that cover most of
.
- The random sums trick Given a collection
of signed functions that may possibly cancel each other in a deterministic sum
, one can perform a random sum
instead to obtain a random function whose magnitude will usually be comparable to the square function
; this can be made rigorous by concentration of measure results, such as Khintchine’s inequality.
These ideas have since been used repeatedly in harmonic analysis. For instance, I used the random rotations trick in a recent paper with Jordan Ellenberg and Richard Oberlin on Kakeya-type estimates in finite fields. The random sums trick is by now a standard tool to build various counterexamples to estimates (or to convergence results) in harmonic analysis, for instance being used by Fefferman in his famous paper disproving the boundedness of the ball multiplier on for
,
. Another use of the random sum trick is to show that Theorem 1 fails once
; see Stein’s original paper for details.
Another use of the random rotations trick, closely related to Theorem 1, is the Nikishin-Stein factorisation theorem. Here is Stein’s formulation of this theorem:
Theorem 2 (Stein factorisation theorem) Let
be a compact group, let
be a homogeneous space of
with a finite Haar measure
, let
and
, and let
be a bounded linear operator commuting with translations and obeying the estimate
for all
and some
. Then
also maps
to
, with
for all
, with
depending only on
.
This result is trivial with , but becomes useful when
. In this regime, the translation invariance allows one to freely “upgrade” a strong-type
result to a weak-type
result. In other words, bounded linear operators from
to
automatically factor through the inclusion
, which helps explain the name “factorisation theorem”. Factorisation theory has been developed further by many authors, including Maurey and Pisier.
Stein’s factorisation theorem (or more precisely, a variant of it) is useful in the theory of Kakeya and restriction theorems in Euclidean space, as first observed by Bourgain.
In 1970, Nikishin obtained the following generalisation of Stein’s factorisation theorem in which the translation-invariance hypothesis can be dropped, at the cost of excluding a set of small measure:
Theorem 3 (Nikishin-Stein factorisation theorem) Let
be a finite measure space, let
and
, and let
be a bounded linear operator obeying the estimate
for all
and some
. Then for any
, there exists a subset
of
of measure at most
such that
One can recover Theorem 2 from Theorem 3 by an averaging argument to eliminate the exceptional set; we omit the details.
— 1. Sketch of proofs —
We now sketch how Stein’s maximal principle is proven. We may normalise . Suppose the maximal inequality (1) fails for any
. Then, for any
, we can find a non-zero function
such that
By homogeneity, we can arrange matters so that
where .
At present, could be a much smaller set than
:
. But we can amplify
by using the random rotations trick. Let
be a natural number comparable to
, and let
be elements of
, chosen uniformly at random. Each element
of
has a probability
of lying in at least one of the translates
of
. From this and the first moment method, we see that with probability
, the set
has measure
.
Now form the function , where
is the left-translation of
by
, and the
are randomly chosen signs. On the one hand, an application of moment methods (such as the Paley-Zygmund inequality), one can show that each element
of
will be such that
with probability
. On the other hand, an application of Khintchine’s inequality shows that with high probability
will have an
norm bounded by
Now we crucially use the hypothesis to replace the
-summation here by an
summation. Interchanging the
and
norms, we then conclude that with high probability we have
To summarise, using the probabilistic method, we have constructed (for arbitrarily large ) a function
whose
norm is only
in size, but such that
on a subset of
of measure
. By sending
rapidly to infinity and taking a suitable combination of these functions
, one can then create a function
in
such that
is infinite on a set of positive measure, which contradicts the hypothesis of pointwise almost everywhere convergence.
Stein’s factorisation theorem is proven in a similar fashion. For Nikishin’s factorisation theorem, the group translation operations are no longer available. However, one can substitute for this by using the failure of the hypothesis (4), which among other things tells us that if one has a number of small sets
in
whose total measure is at most
, then we can find another function
of small
norm for which
is large on a set
outside of
. Iterating this observation and choosing all parameters carefully, one can eventually establish the result.
Remark 1 A systematic discussion of these and other maximal principles is given in this book of Guzman.

16 comments
Comments feed for this article
12 May, 2011 at 10:45 pm
Ming Wang
Dear Professor Tao, included in $\latex R^n$? Since I am not familar with the concepts compact group and homogeneous space. Thank you very much!
included in $\latex R^n$? Since I am not familar with the concepts compact group and homogeneous space. Thank you very much!
Could you give some useful examples of
[Some material added in this direction – T.]
13 May, 2011 at 10:58 am
shannon7774
In paragraph 4 or 5 you said, “Returning to pointwise almost everywhere convergence, the answer in general is “no”. ” Since the question was whether there is a counterexample, shouldn’t the answer here be “yes”?
[Corrected, thanks – T.]
13 May, 2011 at 2:03 pm
Anonymous
Dear Prof. Tao
In the first paragraph I believe it should read “conclude that T_n f converges”
instead of T f_n
[Corrected, thanks – T.]
24 May, 2011 at 4:16 pm
Sixth Linkfest
[…] Tao: Stein’s maximal principle, Stein’s spherical maximal theorem, Locally compact topological vector […]
4 August, 2011 at 4:32 am
Andrew Bailey
Small typo when you talk about Bochner-Riesz multipliers in the second paragraph after the statement of Theorem 1: “depsite”. [Corrected, thanks – T.]
26 August, 2011 at 2:00 am
Anonymous
Dear Prof. Tao,
1)Minor typo: general version instead of “general vesion” in the first line after Theorem 1.
2)I don’t understand this sentence:
On the one hand, an application of moment methods (such as the Paley-Zygmund inequality), one can show that each element {x} of {g_1 E \cup \ldots \cup g_m E} will be such that {|T_* F(x)| \gtrsim 1} with probability {\sim 1}.
If someone (Prof Tao?) could give one or two lines on this… Thanks
26 August, 2011 at 8:16 am
Terence Tao
Thanks for the correction. The Paley-Zygmund inequality can be used to show that if one has a sequence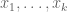 of real numbers with
of real numbers with 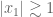 , and one forms the random sum
, and one forms the random sum  , then one has
, then one has 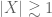 with probability
with probability  (this is basically because
(this is basically because 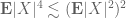 , which is a special case of Khintchine’s inequality; it also reflects the intuitive fact that random walks cannot converge to the origin). If one applies this fact to the numbers
, which is a special case of Khintchine’s inequality; it also reflects the intuitive fact that random walks cannot converge to the origin). If one applies this fact to the numbers  , where n is chosen to make
, where n is chosen to make 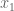 large, one obtains the claim.
large, one obtains the claim.
28 August, 2011 at 10:11 pm
Anonymous
Thank you very much!
13 January, 2014 at 1:11 pm
Anonymous
Must the operator in Theorem 3 commute with translations ?
[Ah, that is a typo, the hypothesis should be removed, thanks – T.]
30 August, 2014 at 9:40 am
Anonymous
Dear Prof. Tao,
In the paragraph where the random rotation trick is introduced, you said “one can randomly select about ${|G|/|E|}$ translates ${g_i E}$ of ${E}$ that cover most of ${X}$”, should it be ${|X|/|E|}$ instead of ${|G|/|E|}$?
[Corrected, thanks – T.]
18 March, 2020 at 12:58 pm
Anonymous
Dear Prof. Tao,
I saw an article about restriction problem for hyperbolic paraboloid in J. Funct. Anal. claim that the Stein’s factorisation theorem (maybe a variant) works for parabolic setting, but with no proof. Could you please tell me if this is obvious? as I only see Bourgain apply the factorisation theorem for spherical restriction.
22 April, 2020 at 10:00 pm
extremal010101
Under the assumptions of Theorem 1 with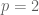 , can one conclude (1) where in the left hand side the weak-type norm is replaced by the strong norm
, can one conclude (1) where in the left hand side the weak-type norm is replaced by the strong norm  ?
?
23 April, 2020 at 7:50 am
Terence Tao
Interesting question! My inclination would be that the answer is “no”, even when say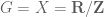 , but I do not have an explicit counterexample. Carleson’s theorem proved the weak type (2,2) of the Carleson maximal operator, but the strong type (2,2) did not seem to obviously follow as a consequence, and was only proven later by the
, but I do not have an explicit counterexample. Carleson’s theorem proved the weak type (2,2) of the Carleson maximal operator, but the strong type (2,2) did not seem to obviously follow as a consequence, and was only proven later by the 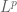 extension of Carleson’s result due to Hunt. There have since been several subsequent proofs of Carleson’s theorem (see eg https://arxiv.org/abs/math/0307008), but from memory the weak type (2,2) is always strictly easier to prove than the strong type (2,2), suggesting that there is no general implication of this form. But this is not yet a formal proof.
extension of Carleson’s result due to Hunt. There have since been several subsequent proofs of Carleson’s theorem (see eg https://arxiv.org/abs/math/0307008), but from memory the weak type (2,2) is always strictly easier to prove than the strong type (2,2), suggesting that there is no general implication of this form. But this is not yet a formal proof.
23 April, 2020 at 8:02 am
Mark Lewko
This is false, as was pointed out to me by Fedja Nazarov: https://mathoverflow.net/a/25552/630.
14 May, 2020 at 7:26 am
247B, Notes 4: almost everywhere convergence of Fourier series | What's new
[…] inequality; see for instance this previous blog post. A remarkable observation of Stein, known as Stein’s maximal principle, allows one to reverse this implication in certain cases by exploiting a symmetry of the problem. […]
15 April, 2024 at 5:23 am
Anonymous
Dear Prof. Tao,
In Stein maximum principle(Theorem 1), is there any other options to drop or exchange the condition commuting with translations?