LLet be a self-adjoint operator on a finite-dimensional Hilbert space
. The behaviour of this operator can be completely described by the spectral theorem for finite-dimensional self-adjoint operators (i.e. Hermitian matrices, when viewed in coordinates), which provides a sequence
of eigenvalues and an orthonormal basis
of eigenfunctions such that
for all
. In particular, given any function
on the spectrum
of
, one can then define the linear operator
by the formula
which then gives a functional calculus, in the sense that the map is a
-algebra isometric homomorphism from the algebra
of bounded continuous functions from
to
, to the algebra
of bounded linear operators on
. Thus, for instance, one can define heat operators
for
, Schrödinger operators
for
, resolvents
for
, and (if
is positive) wave operators
for
. These will be bounded operators (and, in the case of the Schrödinger and wave operators, unitary operators, and in the case of the heat operators with
positive, they will be contractions). Among other things, this functional calculus can then be used to solve differential equations such as the heat equation
The functional calculus can also be associated to a spectral measure. Indeed, for any vectors , there is a complex measure
on
with the property that
indeed, one can set to be the discrete measure on
defined by the formula
One can also view this complex measure as a coefficient
of a projection-valued measure on
, defined by setting
Finally, one can view as unitarily equivalent to a multiplication operator
on
, where
is the real-valued function
, and the intertwining map
is given by
so that .
It is an important fact in analysis that many of these above assertions extend to operators on an infinite-dimensional Hilbert space , so long as one one is careful about what “self-adjoint operator” means; these facts are collectively referred to as the spectral theorem. For instance, it turns out that most of the above claims have analogues for bounded self-adjoint operators
. However, in the theory of partial differential equations, one often needs to apply the spectral theorem to unbounded, densely defined linear operators
, which (initially, at least), are only defined on a dense subspace
of the Hilbert space
. A very typical situation arises when
is the square-integrable functions on some domain or manifold
(which may have a boundary or be otherwise “incomplete”), and
are the smooth compactly supported functions on
, and
is some linear differential operator. It is then of interest to obtain the spectral theorem for such operators, so that one build operators such as
or to solve equations such as (1), (2), (3), (4).
In order to do this, some necessary conditions on the densely defined operator must be imposed. The most obvious is that of symmetry, which asserts that
for all . In some applications, one also wants to impose positive definiteness, which asserts that
for all . These hypotheses are sufficient in the case when
is bounded, and in particular when
is finite dimensional. However, as it turns out, for unbounded operators these conditions are not, by themselves, enough to obtain a good spectral theory. For instance, one consequence of the spectral theorem should be that the resolvents
are well-defined for any strictly complex
, which by duality implies that the image of
should be dense in
. However, this can fail if one just assumes symmetry, or symmetry and positive definiteness. A well-known example occurs when
is the Hilbert space
,
is the space of test functions, and
is the one-dimensional Laplacian
. Then
is symmetric and positive, but the operator
does not have dense image for any complex
, since
for all test functions , as can be seen from a routine integration by parts. As such, the resolvent map is not everywhere uniquely defined. There is also a lack of uniqueness for the wave, heat, and Schrödinger equations for this operator (note that there are no spatial boundary conditions specified in these equations).
Another example occurs when ,
,
is the momentum operator
. Then the resolvent
can be uniquely defined for
in the upper half-plane, but not in the lower half-plane, due to the obstruction
for all test functions (note that the function
lies in
when
is in the lower half-plane). For related reasons, the translation operators
have a problem with either uniqueness or existence (depending on whether
is positive or negative), due to the unspecified boundary behaviour at the origin.
The key property that lets one avoid this bad behaviour is that of essential self-adjointness. Once is essentially self-adjoint, then spectral theorem becomes applicable again, leading to all the expected behaviour (e.g. existence and uniqueness for the various PDE given above).
Unfortunately, the concept of essential self-adjointness is defined rather abstractly, and is difficult to verify directly; unlike the symmetry condition (5) or the positive condition (6), it is not a “local” condition that can be easily verified just by testing on various inputs, but is instead a more “global” condition. In practice, to verify this property, one needs to invoke one of a number of a partial converses to the spectral theorem, which roughly speaking asserts that if at least one of the expected consequences of the spectral theorem is true for some symmetric densely defined operator
, then
is self-adjoint. Examples of “expected consequences” include:
- Existence of resolvents
(or equivalently, dense image for
);
- Existence of a contractive heat propagator semigroup
(in the positive case);
- Existence of a unitary Schrödinger propagator group
;
- Existence of a unitary wave propagator group
(in the positive case);
- Existence of a “reasonable” functional calculus.
- Unitary equivalence with a multiplication operator.
Thus, to actually verify essential self-adjointness of a differential operator, one typically has to first solve a PDE (such as the wave, Schrödinger, heat, or Helmholtz equation) by some non-spectral method (e.g. by a contraction mapping argument, or a perturbation argument based on an operator already known to be essentially self-adjoint). Once one can solve one of the PDEs, then one can apply one of the known converse spectral theorems to obtain essential self-adjointness, and then by the forward spectral theorem one can then solve all the other PDEs as well. But there is no getting out of that first step, which requires some input (typically of an ODE, PDE, or geometric nature) that is external to what abstract spectral theory can provide. For instance, if one wants to establish essential self-adjointness of the Laplace-Beltrami operator on a smooth Riemannian manifold
(using
as the domain space), it turns out (under reasonable regularity hypotheses) that essential self-adjointness is equivalent to geodesic completeness of the manifold, which is a global ODE condition rather than a local one: one needs geodesics to continue indefinitely in order to be able to (unitarily) solve PDEs such as the wave equation, which in turn leads to essential self-adjointness. (Note that the domains
and
in the previous examples were not geodesically complete.) For this reason, essential self-adjointness of a differential operator is sometimes referred to as quantum completeness (with the completeness of the associated Hamilton-Jacobi flow then being the analogous classical completeness).
In these notes, I wanted to record (mostly for my own benefit) the forward and converse spectral theorems, and to verify essential self-adjointness of the Laplace-Beltrami operator on geodesically complete manifolds. This is extremely standard analysis (covered, for instance, in the texts of Reed and Simon), but I wanted to write it down myself to make sure that I really understood this foundational material properly.
— 1. Self-adjointness and resolvents —
To begin, we study what we can abstractly say about a densely defined symmetric linear operator on a Hilbert space
. To avoid some technical issues we shall assume that the Hilbert space is separable, which is the case typically encountered in applications (particularly in PDE). We will occasionally assume also that
is positive, but will make this hypothesis explicit whenever we are doing so.
All convergence in Hilbert spaces will be in the strong (i.e. norm) topology unless otherwise stated. Similarly, all inner products and norms will be over unless otherwise stated.
For technical reasons, it is convenient to reduce to the case when is closed, which means that the graph
is a closed subspace of
. Equivalently,
is closed if whenever
is a sequence converging strongly to a limit
, and
converges to a limit
in
, then
and
. For instance, thanks to the closed graph theorem, an everywhere-defined linear operator is closed if and only if it is bounded.
Not every densely defined symmetric linear operator is closed (indeed, one could take a closed operator and restrict the domain of definition to a proper dense subspace). However, all such operators are closable, in that they have a closure:
Lemma 1 (Closure) Let
be a densely defined symmetric linear operator. Then there exists a unique extension
of
as a closed, densely defined symmetric linear operator, such that the graph
of
is the closure of the graph
of
.
Proof: The key step is to show that the closure of the graph of
remains a graph, i.e. it obeys the vertical line test. If this failed, then by linearity one could find a sequence
converging to zero such that
converged to a non-zero limit
. Since
is dense, we can find
such that
. But then by symmetry
On the other hand, as ,
. Thus
is the graph of some function
. It is easy to see that this is a densely defined symmetric linear operator extending
, and is the unique such operator.
Exercise 1 Show that
is positive if and only if
is positive.
Remark 1 We caution that
is not the closure or completion of
with respect to the usual norm
on
. (Indeed, as
is a dense subspace of
, that completion of
is simply
.) However, it is the completion of
with respect to the modified norm
.
In PDE applications, the closure tends to be defined on a Sobolev space of functions that behave well at the boundary, and is given by a distributional derivative. Here is a simple example of this:
Exercise 2 Let
be the Laplacian
, defined on the dense subspace
of
. Show that the closure
is defined on the Sobolev space
, defined as the completion of
under the Sobolev norm
and that the action of
is given by the weak (distributional) derivative,
.
Next, we define the adjoint of
, which informally speaking is the maximally defined operator for which one has the relationship
for and
. More formally, define
to be the set of all vectors
for which the map
is a bounded linear functional on
, which thus extends to the closure
of
. For such
, we may apply the Riesz representation theorem for Hilbert spaces and locate a unique vector
for which (7) holds. This is easily seen to define a linear operator
. Furthermore, the claim that
is symmetric can be reformulated as the claim that
extends
.
If is not symmetric, then
does not extend
, and need not be densely defined at all. However, it is still closed:
Exercise 3 Let
be a densely defined linear operator, and let
be its adjoint. Show that
is the orthogonal complement in
of (the closure of)
. Conclude that
is always closed.
If
is symmetric, show that
and
.
Exercise 4 Construct an example of a densely defined linear operator
in a separable Hilbert space
for which
is only defined at
. (Hint: Build a dense linearly independent basis of
, let
be the algebraic span of that basis, and design
so that the graph of
is dense in
.)
We caution that the adjoint of a symmetric densely defined operator
need not be itself symmetric, despite extending the symmetric operator
:
Exercise 5 We continue Example 2. Show that for any complex number
, the functions
lie in
with
. Deduce that
is not symmetric, and not positive.
Intuitively, the problem here is that the domain of is too “small” (it stays too far away from the boundary), which makes the domain of
too “large” (it contains too much stuff coming from the boundary), which ruins the integration by parts argument that gives symmetry.
Now we can define (essential) self-adjointness.
Definition 2 Let
be a densely defined linear operator.
is self-adjoint if
. (Note that this implies in particular that
is symmetric and closed.)
is essentially self-adjoint if it is symmetric, and its closure
is self-adjoint.
Note that this extends the usual definition of self-adjointness for bounded operators. Conversely, from the closed graph theorem we also observe the Hellinger-Toeplitz theorem: an operator that is self-adjoint and everywhere defined, is necessarily bounded.
Exercise 6 Let
be a densely defined symmetric closed linear operator. Show that
is self-adjoint if and only if
is symmetric.
It is not immediately obvious what advantage self-adjointness gives. To see this, we consider the problem of inverting the operator for some complex number
, where
is densely defined, symmetric, and closed. Observe that if
, then
is necessarily real. In particular,
and hence by the Cauchy-Schwarz inequality
In particular, if is strictly complex (i.e. not real), then
is injective. Furthermore, we see that if
is such that
is convergent, then by (8)
is convergent also, and hence
is convergent. As
was assumed to be closed, we conclude that
converges to a limit
in
, and
converges to
. As a consequence, we see that the space
is a closed subspace of
. From (8) we then see that we can define an inverse
of
, which we call the resolvent of
with spectral parameter
; this is a bounded linear operator with norm
.
Exercise 7 If
is densely defined, symmetric, closed, and positive, and
is a complex number with
, show
is well-defined on
with
.
Now we observe a connection between self-adjointness and the domain of the resolvent. We first need some basic properties of the resolvent:
Exercise 8 Let
be densely defined, symmetric, and closed.
- (i) (Resolvent identity) If
are distinct strictly complex numbers with
everywhere defined, show that
. (Hint: compute
two different ways.)
- (ii) If
is a strictly complex number with
and
everywhere defined, show that
.
Proposition 3 Let
be densely defined, symmetric, and closed, let
be the adjoint, and let
be strictly complex.
- (i) (Surjectivity is dual to injectivity)
is everywhere defined if and only if the operator
has trivial kernel.
- (ii) (Self-adjointness implies surjectivity) If
is self-adjoint, then
is everywhere defined.
- (iii) (Surjectivity implies self-adjointness) Conversely, if
and
are both everywhere defined, then
is self-adjoint.
In particular, we see that we have a criterion for self-adjointness: a densely defined symmetric closed operator is self-adjoint if and only if and
are both everywhere defined, or in other words if
and
are both surjective.
Proof: We first prove (i). If is not everywhere defined, then the closed subspace
is not all of
. Thus there must be a non-zero vector
in the orthogonal complement of this subspace, thus
for all
. In particular,
and hence, by definition of ,
lies in
. Now from (7) we have
for all ; since
is dense, we have
as required. The converse implication follows by reversing these steps.
Now we prove (ii). Suppose that was not everywhere defined. By (i) and self-adjointness, we conclude that
for some non-zero
. But this contradicts (8).
Now we prove (iii). Let ; our task is to show that
. From Exercise 8(ii) and (7) one has
for all . We conclude that
. Since
takes values in
, the claim follows.
Exercise 9 Let
be densely defined, symmetric, and closed, and let
be strictly complex.
- (i) If
is everywhere defined, show that
is everywhere defined whenever
. (Hint: use Neumann series.)
- (ii) If
is everywhere defined, show that
is everywhere defined whenever
has the same sign as
.
- (iii) If
is positive, and
is not a non-negative real, show that
is everywhere defined if and only if
is self-adjoint.
As a particular corollary of the above exercise, we see that a densely defined, symmetric closed positive operator is self-adjoint if and only if
is everywhere defined, or in other words if
is surjective.
Exercise 10 Let
be a measure space with a countably generated
-algebra (so that
is separable), let
be a measurable function, and let
be the space of all
such that
. Show that the multiplier operator
defined by
is a densely defined self-adjoint operator.
Exercise 11 Let
,
, and
is the momentum operator
. Show that
is densely defined and symmetric, and
is everywhere defined, but
is only defined on the orthogonal complement of
. (Here, we define the resolvent of a closable operator to be the resolvent of its closure.) In particular,
is not self-adjoint.
Exercise 12 Let
be densely defined and symmetric.
- (i) Show that
is essentially self-adjoint if and only if
and
are dense in
.
- (ii) If
is positive, show that
is essentially self-adjoint if and only if
is dense in
.
Exercise 13 Let
and
be sequences of real numbers, with the
all non-zero. Define the Jacobi operator
from the space
of compactly supported sequences
to the space
of square-summable sequences
by the formula
with the convention that
vanishes for
.
- (i) Show that
is densely defined and symmetric.
- (ii) Show that
is essentially self-adjoint if and only if the (unique) solution
to the recurrence
with
(and the convention
), is not square-summable.
This exercise shows that the self-adjointness of an operator, even one as explicit as a Jacobi operator, can depend in a rather subtle and “global” fashion on the behaviour of the coefficients of that oeprator.
— 2. Self-adjointness and spectral measure —
We have seen that self-adjoint operators have everywhere-defined resolvents for all strictly complex
. Now we use this fact to build spectral measures. We will need a useful tool from complex analysis, which places a one-to-one correspondence between finite non-negative measures on
and certain analytic functions on the upper half-plane:
Theorem 4 (Herglotz representation theorem) Let
be an analytic function from the upper half-plane
to the closed upper half-plane
, obeying a bound of the form
for all
and some
. Then there exists a finite non-negative Radon measure
on
such that
We set the proof of the above theorem as an exercise below. Note in the converse direction that if is a finite non-negative Radon measure, then the function
defined by (9) obeys all the hypotheses of the theorem. The Herglotz representation theorem, like the more well known Riesz representation theorem for measures, is a useful tool to construct non-negative Radon measures; later on we will also use Bochner’s theorem for a similar purpose.
Exercise 14 Let
be as in the hypothesis of the Herglotz representation theorem. For each
, let
be the function
.
- (i) Show that one has
for all
, where
is the Poisson kernel and
is the usual convolution operation.
- (ii) Show that the non-negative measures
have a finite mass independent of
, and converge in the vague topology as
to a non-negative finite measure
.
- (iii) Prove the Herglotz representation theorem.
Now we return to spectral theory. Let be a densely-defined self-adjoint operator, and let
. We consider the function
on the upper half-plane. We can use this function and the Herglotz representation theorem to construct spectral measures :
Exercise 15 Let
,
, and
be as above.
- (i) Show that
is analytic. (Hint: use Neumann series and Morera’s theorem.)
- (ii) Show that
for all
in the upper half-plane.
- (iii) Show that
for all
in the upper half-plane. (Hint: You will find Exercise 8 to be useful.)
- (iv) Show that
for all
. (Hint: first show this for
, writing
for some
.)
- (v) Show that there is a non-negative Radon measure
of total mass
such that
for all
in either the upper or lower half-plane.
- (vi) If
is positive, show that
is supported in the right half-line
.
We can depolarise these measures by defining
to obtain complex measures for any
such that
for all in either the upper or lower half-plane. From duality we see that this uniquely defines
. In particular,
depends sesquilinearly on
, and
. Also, since each
has mass
, we see that the inner product
can be recovered from the spectral measure
:
Exercise 16 With the above notation and assumptions, establish the bound
for all
. In particular, for any bounded Borel-measurable function
, there exists a unique bounded operator
such that
Thus, for instance is the identity when
, and
when
.
We have just created a map from the bounded Borel-measurable functions
on
, to the bounded operators
on
. Now we verify some basic properties of this map.
Exercise 17 (Bounded functional calculus) Let
be a self-adjoint densely defined operator, and let
be as above.
- (i) Show that the map
is
-linear. In particular, if
is real-valued, then
is self-adjoint.
- (ii) For any
and any strictly complex
, show that
. (Hint: use the resolvent identity.)
- (iii) For any
and any
, show that
.
- (iv) Show that the map
is a
-homomorphism. In particular,
and
commute for all
.
- (v) Show that
for all
. Improve the
to
. (Hint: to get this improvement, use the
identity
and the tensor power trick.)
- (vi) For any Borel subset
of
, show that
is an orthogonal projection of
. Show that
is a countably additive projection-valued measure, thus
for any sequence of disjoint Borel
, where the convergence is in the strong operator topology.
- (vii) For any bounded Borel set
, show that the image of
lies in
.
- (viii) Show that for any
and
, one has
.
- (ix) Let
be the union of the images of
for
. Show that
is a dense subspace of
(and hence of
), and that
maps
to
.
- (x) Show that
is the space of all functions
such that
. Conclude in particular that
maps
to
for all
.
- (xi) If
is such that
for all
, show that
takes values in
, that
for all
, and
for all
.
- (xii) Let
be the space of all
such that
is not invertible. Show that
is a closed set which is the union of the supports of the
as
range over
. In particular,
, and
when
is positive. Show that
is the identity map.
- (xiii) Extend the bounded functional calculus from the bounded Borel measurable functions
on
to the bounded measurable functions
on the spectrum
(i.e. show that the previous statements (i)-(xi) continue to hold after
is replaced by
throughout).
The above collection of facts (or various subcollections thereof) is often referred to as the spectral theorem. It is stated for self-adjoint operators, but one can of course generalise the spectral theorem to essentially self-adjoint operators by applying the spectral theorem to the closure. (One has to replace the domain of
by the domain
of the closure
, of course, when doing so.)
Exercise 18 (Spectral measure and eigenfunctions) Let the notation be as in the preceding exercise, and let
. Show that the space
is the range of the projection
. In particular,
has an eigenfunction at
if and only if
is non-trivial.
We have seen how the existence of resolvents gives us a bounded functional calculus (i.e. the conclusions in the above exercise). Conversely, if a symmetric densely defined closed operator has a bounded functional calculus, one can define the resolvents
simply as
, where
. Thus we see that the existence of a bounded functional calculus is equivalent to the existence of resolvents, which by the previous discussion is equivalent to self-adjointness.
Using the bounded functional calculus, one can not only recover the resolvents , but can now also build Schrödinger propagators
, and when
is positive definite one can also build heat operators
for
and wave operators
for
(and also define resolvents
for negative choices
of the spectral parameter). We will study these operators more in the next section.
Exercise 19 (Locally bounded functional calculus) Let
be a densely defined self-adjoint operator, and let
be the space of Borel-measurable functions from
to
which are bounded on every bounded set.
- Show that for every
there is a unique linear operator
such that
whenever
.
- (i) Show that the map
is a
-homomorphism.
- (ii) Show that when
is actually bounded (rather than merely locally bounded), then this definition of
agrees with that in the preceding exercise (after restricting from
to
).
- (iii) Show that
, where
is the identity map
.
- (iv) State and prove a rigorous version of the formal assertion that
and more generally
Now we use the spectral theorem to place self-adjoint operators in a normal form. Let us say that two operators and
are unitarily equivalent if there is a unitary map
with
and
. It is easy to see that all the constructions given above (such as the bounded functional calculus) are preserved by unitary equivalence.
If is a densely defined self-adjoint operator, define an invariant subspace to be a subspace
of
such that
for all
. We say that a vector
is a cyclic vector for
if the set
is dense in
.
Exercise 20
- (i) Show that if
is an invariant subspace of
, then so is
, and furthermore the orthogonal projections to
and
commute with
for every
.
- (ii) Show that if
is a invariant subspace of
, then the restriction
of
to
is a densely defined self-adjoint operator on
with
. Furthermore, one has
for all
.
- (iii) Show that
decomposes as a direct sum
, where the index set
is at most countable, and each
is a closed invariant subspace of
(with the
mutually orthogonal), such that each
has a cyclic vector
. (Hint: use Zorn’s lemma and the separability of
.)
- (iv) If
has a cyclic vector
, show that
is unitarily conjugate to a multiplication operator
on
for some non-negative Radon measure
, defined on the domain
.
- (v) For general
, show that
is unitarily conjugate to a multiplication operator
on
for some measure space
with a countably generated
-algebra and some measurable
, defined on the domain
.
The above exercise gives a satisfactory concrete description of a self-adjoint operator (up to unitary equivalence) as a multiplication operator on some measure space , although we caution that this equivalence is not canonical (there is some flexibility in the choice of the underlying measure space
and multiplier
, as well as the unitary conjugation map).
Exercise 21 Let
be a self-adjoint densely defined operator.
- (i) Show that
is positive if and only if
.
- (ii) Show that
is bounded if and only if
is bounded. Furthermore, in this case we have
.
- (iii) Show that
is trivial if and only if
is empty.
— 3. Self-adjointness and flows —
Now we relate self-adjointness to a variety of flows, beginning with the heat flow.
Exercise 22 Let
be a self-adjoint positive densely defined operator, and for each
, let
be the heat operator
.
- (i) Show that for each
,
is a bounded self-adjoint operator of norm at most
, that the map
is continuous in the strong operator topology, and such that
and
for all
. (The latter two properties are asserting that
is a one-parameter semigroup.)
- (ii) Show that for any
,
converges to
as
.
- (iii) Conversely, if
is not in
, show that
does not converge as
.
We remark that the above exercise can be viewed as a special case of the Hille-Yoshida theorem.
We now establish a converse to the above statement:
Theorem 5 Let
be a separable Hilbert space, and suppose one has a family
of bounded self-adjoint operators of norm at most
for each
, which is continuous in the strong operator topology, and such that
and
for all
. Then there exists a unique self-adjoint positive densely defined operator
such that
for all
.
We leave the proof of this result to the exercise below. The basic idea is to somehow use the identity
which suggests that
which should allow one to recover from the
.
Exercise 23 Let the notation be as in the above theorem.
- (i) Establish the uniqueness claim. (Hint: use Exercise 22.)
- (ii) Let
be the operator
Show that
is well-defined, bounded, positive semidefinite, and self-adjoint, with operator norm at most one, and that
commutes with all the
.
- (iii) Show that the spectrum of
lies in
, but that
has no eigenvalue at
.
- (iv) Show that there exists a densely defined self-adjoint operator
such that
is the identity on
and
is the identity on
.
- (v) Show that
is densely defined self-adjoint and positive definite, and commutes with all the
.
- (vi) Show that for all
and
, one has
and
, where the derivatives are in the classical limiting Newton quotient sense (in the strong topology of
).
- (vii) Conclude the proof of Theorem 5. (Hint: show that
is non-positive.)
The above exercise gives an important way to establish essential self-adjointness, namely by solving the heat equation (1):
Exercise 24 Let
be a densely defined symmetric positive definite operator. Suppose that for every
there exists a continuously differentiable solution
to (1). Show that
is essentially self-adjoint. (Hint: by investigating
, establish the uniqueness of solutions to the heat equation, which allows one to define linear contractions
. To establish self-adjointness of the
, take an inner product of a solution to the heat equation against a time-reversed solution to the heat equation, and differentiate that inner product in time. Now apply the preceding exercises to obtain a self-adjoint extension
of
. To show that
is the closure of
, it suffices to show that
is dense in
with the inner product
. But if
is not dense in
, then it has a non-trivial orthogonal complement; apply
to this complement to show that
also has a non-trivial orthogonal complement in
, a contradiction.)
Remark 2 When applying the above criterion for essential self-adjointness, one usually cannot use the space
of compactly supported smooth functions as the dense subspace, because this space is usually not preserved by the heat flow. However, in practice one can get around this by enlarging the class, for instance to the class of Schwartz functions.
Now we obtain analogous results for the Schrödinger propagators . We begin with the analogue of Exercise 22:
Exercise 25 Let
be a self-adjoint densely defined operator, and for each
, let
be the Schrödinger operator
.
- (i) Show that for each
,
is a unitary operator, that the map
is continuous in the strong operator topology, and such that
and
for all
.
- (ii) Show that for any
,
converges to
as
.
- (iii) Conversely, if
is not in
, show that
does not converge as
.
Now we can give the converse, known as Stone’s theorem on one-parameter unitary groups:
Theorem 6 (Stone’s theorem) Let
be a separable Hilbert space, and suppose one has a family
of unitary for each
, which is continuous in the strong operator topology, and such that
and
for all
. Then there exists a unique self-adjoint densely defined operator
such that
for all
.
We outline a proof of this theorem in an exercise below, based on using the group to build spectral measure.
Exercise 26 Let the notation be as in the above theorem.
- (i) Establish the uniqueness component of Stone’s theorem.
- (ii) Show that for any
, there is a non-negative Radon measure
of total mass
such that
for all
. (Hint: use Bochner’s theorem, a proof of which (at least on
, which is the case of interest here) can be found for instance in these notes.)
- (iii) Show that for any
, there is a unique complex measure
such that
for all
. Show that
is sesquilinear in
with
.
- (iv) Show that for any
, there is a unique bounded operator
such that
for all
.
- (v) Show that
for all
and
.
- (vi) Show that the map
is a *-homomorphism from
to
.
- (vii) Show that there is a projection-valued measure
with
, such that for every
, the complex measure
is such that
for all
.
- (viii) Show that there exists a self-adjoint densely defined operator
whose spectral measure is
.
- (ix) Conclude the proof of Stone’s theorem.
Exercise 27 Let
be a densely defined symmetric operator. Suppose that for every
there exists a continuously differentiable solution
to (2). Show that
is essentially self-adjoint.
We can now see a clear link between essential self-adjointness and completeness, at least in the case of scalar first-order differential operators:
Exercise 28 Let
be a smooth manifold with a smooth measure
, and let
be a smooth vector field on
which is divergence-free with respect to the measure
. Suppose that the vector field
is complete in the sense that for any
, there exists a global smooth solution
to the ODE
with initial data
. Show that the first-order differential operator
is essentially self-adjoint.
Extend the above result to non-divergence-free vector fields, after replacing
with
.
Remark 3 The requirement of completeness is basically necessary; one can still have essential self-adjointness if there are a measure zero set of initial data
for which the trajectories of
are incomplete, but once a positive measure set of trajectories become incomplete, the propagators
do not make sense globally, and so self-adjointness should fail.
Finally, we turn to the relationship between self-adjointness and the wave equation, which is a more complicated variant of the relationship between self-adjointness and the Schrödinger equation. More precisely, we will show the following version of Exercise 27:
Theorem 7 Let
be a densely defined positive symmetric operator. Suppose for every
, there exists a twice continuously differentiable (in
) solution
to (3). Then
is essentially self-adjoint.
(One could also obtain wave equation analogues of Exercise 25 or Theorem 6, but these are somewhat messy to state, and we will not do so here.)
We now prove this theorem. To simplify the exposition, we will assume that is strictly positive, in the sense that
for all non-zero
, and leave the general case as an exercise.
We introduce a new inner product on
by the formula
By hypothesis, this is a Hermitian inner product on . We then define an inner product
on
by the formula
then this is a Hermitian inner product on . We define the energy space
be the completion of
with respect to this inner product; we can factor this as
, where
is the completion of
using the
inner product.
Suppose is a twice continuously differentiable solution to (3) for some
. Then if we define the energy
then one easily computes using (3) that , and so
In particular, if , then
, and so twice continuously differentiable solutions to (3) are unique. This allows us to define wave operators
by defining
. This is clearly linear, and from the energy identity we see that
is an isometry, and thus extends to an isometry on the energy space
. From uniqueness we also see that
is a one-parameter group, i.e. a homomorphism that is continuous in the strong operator topology. In particular, the isometries
are invertible and are thus unitary. By Stone’s theorem, there thus exists a densely defined self-adjoint operator
on some dense subspace
of
such that
for all
.
If , then from the twice differentiability of the solution
to the wave equation, we see that
From Exercise 2, we conclude that and
Now we need to pass from the self-adjointness of to the essential self-adjointness of
. Suppose for contradiction that
was not essentially self-adjoint. Then
does not have dense image, and so there exists a non-zero
such that
for all .
It will be convenient to work with a “band-limited” portion of , to get around the problem that
and
can leave this domain. Let
be a compactly supported even smooth function of total mass one. For any
, define the Littlewood-Paley projection
where is the Schwartz function
. Then (by strong continuity of
) these operators map
to
, commutes with the entire functional calculus of
, and also maps
to
. Also, from functional calculus one sees that
and in particular maps
to
as well.
Let be the reflection operator
. From time reversal of the wave equation, we have
, and thus
commutes with
. In particular, we can write
for some operators and
. Since
preserves
, the operators
preserve
.
For any , we have
combining this with (12) we see that
and
for all . Also, since
preserves
, we see that
preserves
.
We can then expand as
and thus
In particular
for all . By duality (noting that
is a bounded real function of
) we conclude that
But by sending and using the spectral theorem, this implies from monotone convergence that the spectral measure
is zero, and thus
vanishes in
, a contradiction. This establishes the essential self-adjointness of
.
Exercise 29 Establish Theorem 7 without the assumption that
is strictly positive. (Hint: use the Cauchy-Schwarz inequality to show that strict positivity is equivalent to the absence of eigenfunctions with eigenvalue zero, and then quotient out such eigenfunctions.)
— 4. Essential self-adjointness of the Laplace-Beltrami operator —
We now discuss how one can use the above criteria to establish essential self-adjointness of a Laplace-Beltrami operator on a smooth complete Riemannian manifold
, viewed as a densely defined symmetric positive operator on the dense subspace
of
. This result was first established by Gaffney and by Roelcke.
To do this, we have to solve a PDE – either the Helmholtz equation (4) (for some not on the positive real axis), the heat equation (1), the Schrödinger equation (25), or the wave equation (3).
The Schrödinger formalism is quite suggestive. From a semiclassical perspective, the Schrödinger equation associated to the Laplace-Beltrami operator should be viewed as a quantum version of the classical flow associated to the corresponding Hamiltonian
, i.e. geodesic flow. From Exercise 28 we know that the generator of Hamiltonian flows (normalised by
) are essentially self-adjoint when they are complete (note from Liouville’s theorem that such generators are automatically divergence-free with respect to Liouville measure), which suggests that the Schrödinger operator
should be also. Unfortunately, this is not a rigorous argument, and is difficult to make it so due to the nature of the time-dependent Schrödinger equation, which has infinite speed of propagation, and no dissipative properties. In practice, we therefore establish esssential self-adjointness by solving one of the other equations.
To solve any of these equations, it is difficult to solve any of them by an exact formula (unless the manifold is extremely symmetric); but one can proceed by solving them approximately, and using perturbation theory to eliminate the error. This method works as long as the error created by the approximate solution is both sufficiently small and sufficiently smooth that perturbative techniques (such as Neumann series, or the inverse function theorem) become applicable. (This type of method, for instance, is used to deduce essential self-adjointness of various perturbations
of the Laplace-Beltrami operator from the essential self-adjointness of the original operator
.)
For instance, suppose one is trying to solve the Helmholtz equation
for some large real , and some
. For sake of concreteness let us take
to be three-dimensional. If
was a Euclidean space
, then we have an explicit formula
for the solution; note that the exponential decay of will keep
in
as well. Inspired by this, we can try to solve the Helmholtz equation in curved space by proposing as an approximate solution
This is a little problematic because develops singularities after a certain point, but if one has a uniform lower bound on the injectivity radius (here we are implicitly using the hypothesis of completeness), and also uniform bounds on the curvature and its derivatives, one can truncate this approximate solution to the region where
is small, and obtain an approximate solution
whose error
can be made to be smaller in norm than that of
if the spectral parameter
is chosen large enough; we omit the details. From this, we can then solve the Helmholtz equation by Neumann series and thus establish essential self-adjointness. A similar method also works (under the same hypotheses on
) to construct approximate heat kernels, giving another way to establish essential self-adjointness of the Laplace-Beltrami operator.
What about when there is no uniform bound on the geometry? In that case, it is best to work with the wave equation formalism, because the finite speed of propagation property of that equation allows one to localise to compact portions of the manifold for which uniform bounds on the geometry are automatic. Indeed, to solve the wave equation in for some fixed period of time, one can use finite speed of propagation, combined with completeness of the manifold, to work in a compact subset of this manifold, which by suitable alteration of the metric beyond the support of the solution, one can view as a subset of a compact complete manifold. On such manifolds, we already know essential self-adjointness by the previous arguments, so we may solve the wave equation in that setting (one can also solve the wave equation using methods from microlocal analysis, if desired), and then take repeated advantage of finite speed of propagation (which can be proven rigorously by energy methods) to glue together these local solutions to obtain a global solution; we omit the details.
In all these cases, a somewhat nontrivial application of PDE theory is required. Unfortunately, this seems to be inevitable; at some point one must somehow use the hypothesis of completeness of the underlying manifold, and PDE methods are the only known way to connect that hypothesis to the dynamics of the Laplace-Beltrami operator.

25 comments
Comments feed for this article
20 December, 2011 at 6:14 pm
Guest
No need to publish this, just a small correction on Exercise 23:
“To establish self-adjointness of the s(t) , take an inner product of a solution to the heat equation against a time-reversed solution OF the heat equation, and differentiate that inner product in time.”
[Corrected, thanks – T.]
21 December, 2011 at 11:59 am
Lior Silberman
Question: In the definition of adjoint just before Ex 3, it’s not clear to me why contains non-zero vectors at all, let alone why the adjoint is also a densely defined operator. If $L$ is symmetric then obviously
contains non-zero vectors at all, let alone why the adjoint is also a densely defined operator. If $L$ is symmetric then obviously 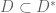 — what happens in general?
— what happens in general?
Typos:
Pf of Lemma 1: last \neq should be a \to , not equal to it. Later, the non-zero vector should be
, not equal to it. Later, the non-zero vector should be 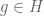 .
. be multiplication by the complex conjugate? [i.e. did you mean for the function to be real valued?]
be multiplication by the complex conjugate? [i.e. did you mean for the function to be real valued?]
Statement of Prop 3(i): R(z) is everywhere defined iff the kernel is trivial.
Pf of Prop 3(i): In the second inline equation, the subspace is contained in
Ex 9: Isn’t the adjoint of multiplication by
Ex 17: missing closing parenthesis at the end.
[Corrected, thanks. In general, the adjoint could well be trivial; I added an exercise to this effect. – T.]
2 January, 2012 at 3:09 am
Александр Шапошников
It seems to me there is a missprint in Exercise 11:
R(i) and R(-i) should be interchanged
[Corrected, thanks – T]
3 January, 2012 at 12:08 pm
Александр Шапошников
There is another small missprint in Exercise 17 should be replaced with
should be replaced with 
(item (x)):
[Corrected, thanks – T.]
19 May, 2012 at 11:35 am
Anonymous
I would like to suggest a minor improvement to Exercise 11. The operator given there is not closed, but the previous text defines the resolvent only in the closed case. This can be a little confusing to the beginner and I suggest that a little note might be added to make explicit that the resolvent of a closable operator is assumed to be the resolvent of the closure. Thank you.
[Suggestion implemented, thanks – T.]
16 September, 2014 at 8:04 am
VMT
Hi! I don’t understand the hint for ex 17.(v): using the fact that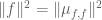 and ex 17.(iii) we directly obtain
and ex 17.(iii) we directly obtain 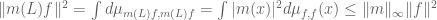 , which already implies
, which already implies  .
.
If this is correct, what did you have in mind when you wrote the hint?
(Sorry for posting a doubt about a 3 years-old entry..)
16 September, 2014 at 8:39 am
Terence Tao
Oh, that’s a nice solution! My solution proceeded by bounding instead, and the depolarisation identity can cost one a factor of 4 or so when one uses that route, if one isn’t being careful. (I’m also very fond of the tensor power trick, so I couldn’t resist an opportunity to sneak it in, even if as it turns out it can be done without in this case.)
instead, and the depolarisation identity can cost one a factor of 4 or so when one uses that route, if one isn’t being careful. (I’m also very fond of the tensor power trick, so I couldn’t resist an opportunity to sneak it in, even if as it turns out it can be done without in this case.)
16 September, 2014 at 9:23 am
VMT
Thank you; so you probably proceeded by bounding in terms of
in terms of 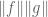 . Still, I don’t understand how one can use the depolarisation identity.. On the other hand, if you use Cauchy-Schwarz you get
. Still, I don’t understand how one can use the depolarisation identity.. On the other hand, if you use Cauchy-Schwarz you get  .
.
If the answer is complicated, never mind!
16 September, 2014 at 9:52 am
Terence Tao
Depolarisation gives a bound of the form which one can then amplify to
which one can then amplify to  by using homogeneity, as in this previous post. But it is true that by using the abstract Cauchy-Schwarz inequality, one can pass directly to
by using homogeneity, as in this previous post. But it is true that by using the abstract Cauchy-Schwarz inequality, one can pass directly to  .
.
16 September, 2014 at 10:03 am
VMT
Ah, now I see. Very instructive, thank you!
28 June, 2018 at 6:25 am
Jack
Hi, Sorry to comment on and old comment of a relatively old post. I am a bit stuck trying to show that directly using Cauchy-Schwarz (CS). It is a consequence of CS that for any measurable subset
directly using Cauchy-Schwarz (CS). It is a consequence of CS that for any measurable subset  ,
,  .
.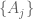 is a finite partition of
is a finite partition of 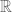 one has:
one has:
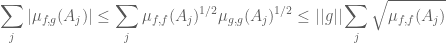 and here I would want to use finite additivity to remove the sum and bound by
and here I would want to use finite additivity to remove the sum and bound by 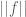 but the square root seems to prevent me from doing so. What is the trick I’m missing ?
but the square root seems to prevent me from doing so. What is the trick I’m missing ?
but then if
28 June, 2018 at 6:39 am
Terence Tao
Hmm, I see now that to get the sharp inequality one needs to already possess the functional calculus, since with that calculus one can write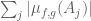 as
as  for some piecewise constant multiplier
for some piecewise constant multiplier  bounded in magnitude by 1. So to avoid circularity one may have to revert back to the depolarisation argument that loses an absolute constant (something like 4), since one does not need the sharp inequality at this stage of the construction.
bounded in magnitude by 1. So to avoid circularity one may have to revert back to the depolarisation argument that loses an absolute constant (something like 4), since one does not need the sharp inequality at this stage of the construction.
16 April, 2015 at 3:26 am
Ramesh
Can you please give a reference for the spectral theorem (multiplication form) for unbounded normal operators
18 August, 2015 at 9:39 am
A wave equation approach to automorphic forms in analytic number theory | What's new
[…] as discussed in this previous post, the spectral theory of an essentially self-adjoint operator such as is basically equivalent to […]
3 May, 2017 at 5:37 am
Anonymous
Would you say something about what would people do if the unbounded linear operator is not densely defined on a Hilbert space? Can it be reduced to the densely defined case?
7 June, 2017 at 3:08 am
Maths student
Can’t you just take the closure of the domain of definition, where the Hermitian form will be the restriction, to obtain a new, smaller Hilbert space, and get a self-map via orthogonal projection?
4 June, 2017 at 11:05 am
Maths student
If the operator is linear and densely defined, but the domain of definition is not a linear space, the ex. 1 seems to require even boundedness of L, even though I didn’t find a counter-example yet.
[In the definition of “densely defined”, the domain of definition is understood to be a linear subspace, not just a set (otherwise it does not makes sense to require $latex $L$ to be linear. -T]
8 June, 2017 at 1:03 am
Maths student
Let be densely defined on a set
be densely defined on a set  ,
,  a complex Hilbert space, and let
a complex Hilbert space, and let 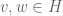 and
and  . We call
. We call  linear iff
linear iff  implies
implies 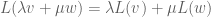 .
.
5 June, 2017 at 1:28 am
Maths student
Dear Prof. Tao,
please add a bar to the L in the equation defining the Sobolev norm in ex. 2, and formulate: “The Sobolev space is defined as the domain of definition of the closed operator \overline L with Sobolev norm…”; indeed, closure can only be taken in spaces where you already have a norm on the larger space, as far as I know (on the other hand, the completion can be performed without any larger space around the space which is to be completed).
[“closure” replaced with “completion” -T.]
2 July, 2017 at 3:46 am
Maths student
Dear Prof. Tao, in the proof of Prop. 3 (i) please replace by
by 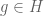 .
.
14 July, 2017 at 8:05 am
Oskar
In exercise 16 and 17 what is being meant with $\ll$?
23 July, 2017 at 9:35 am
Math student
In ex. 14 i) I’m having difficulty finding the right harmonic function to which to apply Liouville’s theorem; of course, the function needs to be defined on a whole real vector space, so I thought that I’d insert the exponential function, but the derivatives don’t want to cancel, in particular since we have a complicated convolution expression in there, which doesn’t seem to be easily evaluated. At this point, after several hours of thought, I raise the white flag. To which harmonic function do I have to apply Liouville?
23 July, 2017 at 2:12 pm
Terence Tao
Oops, I meant to say the maximum principle instead of Liouville’s theorem; I’ve updated the hint accordingly.
23 July, 2017 at 11:37 pm
Maths student
At least, I discovered Nelson’s proof of Liouville’s theorem: Pick any two points, apply the average formula to very large neighbourhoods of these points, and observe that the neighbourhoods are equal up to “small” sets which don’t really perturb the outcome by boundedness.
16 October, 2019 at 4:24 am
Mizar
Speaking of Exercise 14 (i), actually I can’t see it directly using the maximum principle, but rather by (odd) reflection in the hyperplane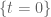 , which gives a bounded harmonic function on
, which gives a bounded harmonic function on 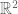 , and concluding with Liouville.
, and concluding with Liouville.
[Fair enough; I’ve removed the hint. -T]