The Poincaré upper half-plane (with a boundary consisting of the real line
together with the point at infinity
) carries an action of the projective special linear group
via fractional linear transformations:
Here and in the rest of the post we will abuse notation by identifying elements of the special linear group
with their equivalence class
in
; this will occasionally create or remove a factor of two in our formulae, but otherwise has very little effect, though one has to check that various definitions and expressions (such as (1)) are unaffected if one replaces a matrix
by its negation
. In particular, we recommend that the reader ignore the signs
that appear from time to time in the discussion below.
As the action of on
is transitive, and any given point in
(e.g.
) has a stabiliser isomorphic to the projective rotation group
, we can view the Poincaré upper half-plane
as a homogeneous space for
, and more specifically the quotient space of
of a maximal compact subgroup
. In fact, we can make the half-plane a symmetric space for
, by endowing
with the Riemannian metric
(using Cartesian coordinates ), which is invariant with respect to the
action. Like any other Riemannian metric, the metric on
generates a number of other important geometric objects on
, such as the distance function
which can be computed to be given by the formula
the volume measure , which can be computed to be
and the Laplace-Beltrami operator, which can be computed to be (here we use the negative definite sign convention for
). As the metric
was
-invariant, all of these quantities arising from the metric are similarly
-invariant in the appropriate sense.
The Gauss curvature of the Poincaré half-plane can be computed to be the constant , thus
is a model for two-dimensional hyperbolic geometry, in much the same way that the unit sphere
in
is a model for two-dimensional spherical geometry (or
is a model for two-dimensional Euclidean geometry). (Indeed,
is isomorphic (via projection to a null hyperplane) to the upper unit hyperboloid
in the Minkowski spacetime
, which is the direct analogue of the unit sphere in Euclidean spacetime
or the plane
in Galilean spacetime
.)
One can inject arithmetic into this geometric structure by passing from the Lie group to the full modular group
or congruence subgroups such as
for natural number , or to the discrete stabiliser
of the point at infinity:
These are discrete subgroups of , nested by the subgroup inclusions
There are many further discrete subgroups of (known collectively as Fuchsian groups) that one could consider, but we will focus attention on these three groups in this post.
Any discrete subgroup of
generates a quotient space
, which in general will be a non-compact two-dimensional orbifold. One can understand such a quotient space by working with a fundamental domain
– a set consisting of a single representative of each of the orbits
of
in
. This fundamental domain is by no means uniquely defined, but if the fundamental domain is chosen with some reasonable amount of regularity, one can view
as the fundamental domain with the boundaries glued together in an appropriate sense. Among other things, fundamental domains can be used to induce a volume measure
on
from the volume measure
on
(restricted to a fundamental domain). By abuse of notation we will refer to both measures simply as
when there is no chance of confusion.
For instance, a fundamental domain for is given (up to null sets) by the strip
, with
identifiable with the cylinder formed by gluing together the two sides of the strip. A fundamental domain for
is famously given (again up to null sets) by an upper portion
, with the left and right sides again glued to each other, and the left and right halves of the circular boundary glued to itself. A fundamental domain for
can be formed by gluing together
copies of a fundamental domain for in a rather complicated but interesting fashion.
While fundamental domains can be a convenient choice of coordinates to work with for some computations (as well as for drawing appropriate pictures), it is geometrically more natural to avoid working explicitly on such domains, and instead work directly on the quotient spaces . In order to analyse functions
on such orbifolds, it is convenient to lift such functions back up to
and identify them with functions
which are
-automorphic in the sense that
for all
and
. Such functions will be referred to as
-automorphic forms, or automorphic forms for short (we always implicitly assume all such functions to be measurable). (Strictly speaking, these are the automorphic forms with trivial factor of automorphy; one can certainly consider other factors of automorphy, particularly when working with holomorphic modular forms, which corresponds to sections of a more non-trivial line bundle over
than the trivial bundle
that is implicitly present when analysing scalar functions
. However, we will not discuss this (important) more general situation here.)
An important way to create a -automorphic form is to start with a non-automorphic function
obeying suitable decay conditions (e.g. bounded with compact support will suffice) and form the Poincaré series
defined by
which is clearly -automorphic. (One could equivalently write
in place of
here; there are good argument for both conventions, but I have ultimately decided to use the
convention, which makes explicit computations a little neater at the cost of making the group actions work in the opposite order.) Thus we naturally see sums over
associated with
-automorphic forms. A little more generally, given a subgroup
of
and a
-automorphic function
of suitable decay, we can form a relative Poincaré series
by
where is any fundamental domain for
, that is to say a subset of
consisting of exactly one representative for each right coset of
. As
is
-automorphic, we see (if
has suitable decay) that
does not depend on the precise choice of fundamental domain, and is
-automorphic. These operations are all compatible with each other, for instance
. A key example of Poincaré series are the Eisenstein series, although there are of course many other Poincaré series one can consider by varying the test function
.
For future reference we record the basic but fundamental unfolding identities
for any function with sufficient decay, and any
-automorphic function
of reasonable growth (e.g.
bounded and compact support, and
bounded, will suffice). Note that
is viewed as a function on
on the left-hand side, and as a
-automorphic function on
on the right-hand side. More generally, one has
whenever are discrete subgroups of
,
is a
-automorphic function with sufficient decay on
, and
is a
-automorphic (and thus also
-automorphic) function of reasonable growth. These identities will allow us to move fairly freely between the three domains
,
, and
in our analysis.
When computing various statistics of a Poincaré series , such as its values
at special points
, or the
quantity
, expressions of interest to analytic number theory naturally emerge. We list three basic examples of this below, discussed somewhat informally in order to highlight the main ideas rather than the technical details.
The first example we will give concerns the problem of estimating the sum
where is the divisor function. This can be rewritten (by factoring
and
) as
which is basically a sum over the full modular group . At this point we will “cheat” a little by moving to the related, but different, sum
This sum is not exactly the same as (8), but will be a little easier to handle, and it is plausible that the methods used to handle this sum can be modified to handle (8). Observe from (2) and some calculation that the distance between and
is given by the formula
and so one can express the above sum as
(the factor of coming from the quotient by
in the projective special linear group); one can express this as
, where
and
is the indicator function of the ball
. Thus we see that expressions such as (7) are related to evaluations of Poincaré series. (In practice, it is much better to use smoothed out versions of indicator functions in order to obtain good control on sums such as (7) or (9), but we gloss over this technical detail here.)
The second example concerns the relative
of the sum (7). Note from multiplicativity that (7) can be written as , which is superficially very similar to (10), but with the key difference that the polynomial
is irreducible over the integers.
As with (7), we may expand (10) as
At first glance this does not look like a sum over a modular group, but one can manipulate this expression into such a form in one of two (closely related) ways. First, observe that any factorisation of
into Gaussian integers
gives rise (upon taking norms) to an identity of the form
, where
and
. Conversely, by using the unique factorisation of the Gaussian integers, every identity of the form
gives rise to a factorisation of the form
, essentially uniquely up to units. Now note that
is of the form
if and only if
, in which case
. Thus we can essentially write the above sum as something like
and one the modular group is now manifest. An equivalent way to see these manipulations is as follows. A triple
of natural numbers with
gives rise to a positive quadratic form
of normalised discriminant
equal to
with integer coefficients (it is natural here to allow
to take integer values rather than just natural number values by essentially doubling the sum). The group
acts on the space of such quadratic forms in a natural fashion (by composing the quadratic form with the inverse
of an element
of
). Because the discriminant
has class number one (this fact is equivalent to the unique factorisation of the gaussian integers, as discussed in this previous post), every form
in this space is equivalent (under the action of some element of
) with the standard quadratic form
. In other words, one has
which (up to a harmless sign) is exactly the representation ,
,
introduced earlier, and leads to the same reformulation of the sum (10) in terms of expressions like (11). Similar considerations also apply if the quadratic polynomial
is replaced by another quadratic, although one has to account for the fact that the class number may now exceed one (so that unique factorisation in the associated quadratic ring of integers breaks down), and in the positive discriminant case the fact that the group of units might be infinite presents another significant technical problem.
Note that has real part
and imaginary part
. Thus (11) is (up to a factor of two) the Poincaré series
as in the preceding example, except that
is now the indicator of the sector
.
Sums involving subgroups of the full modular group, such as , often arise when imposing congruence conditions on sums such as (10), for instance when trying to estimate the expression
when
and
are large. As before, one then soon arrives at the problem of evaluating a Poincaré series at one or more special points, where the series is now over
rather than
.
The third and final example concerns averages of Kloosterman sums
where and
is the inverse of
in the multiplicative group
. It turns out that the
norms of Poincaré series
or
are closely tied to such averages. Consider for instance the quantity
where is a natural number and
is a
-automorphic form that is of the form
for some integer and some test function
, which for sake of discussion we will take to be smooth and compactly supported. Using the unfolding formula (6), we may rewrite (13) as
To compute this, we use the double coset decomposition
where for each ,
are arbitrarily chosen integers such that
. To see this decomposition, observe that every element
in
outside of
can be assumed to have
by applying a sign
, and then using the row and column operations coming from left and right multiplication by
(that is, shifting the top row by an integer multiple of the bottom row, and shifting the right column by an integer multiple of the left column) one can place
in the interval
and
to be any specified integer pair with
. From this we see that
and so from further use of the unfolding formula (5) we may expand (13) as
The first integral is just . The second expression is more interesting. We have
so we can write
as
which on shifting by
simplifies a little to
and then on scaling by
simplifies a little further to
Note that as , we have
modulo
. Comparing the above calculations with (12), we can thus write (13) as
where
is a certain integral involving and a parameter
, but which does not depend explicitly on parameters such as
. Thus we have indeed expressed the
expression (13) in terms of Kloosterman sums. It is possible to invert this analysis and express varius weighted sums of Kloosterman sums in terms of
expressions (possibly involving inner products instead of norms) of Poincaré series, but we will not do so here; see Chapter 16 of Iwaniec and Kowalski for further details.
Traditionally, automorphic forms have been analysed using the spectral theory of the Laplace-Beltrami operator on spaces such as
or
, so that a Poincaré series such as
might be expanded out using inner products of
(or, by the unfolding identities,
) with various generalised eigenfunctions of
(such as cuspidal eigenforms, or Eisenstein series). With this approach, special functions, and specifically the modified Bessel functions
of the second kind, play a prominent role, basically because the
-automorphic functions
for and
non-zero are generalised eigenfunctions of
(with eigenvalue
), and are almost square-integrable on
(the
norm diverges only logarithmically at one end
of the cylinder
, while decaying exponentially fast at the other end
).
However, as discussed in this previous post, the spectral theory of an essentially self-adjoint operator such as is basically equivalent to the theory of various solution operators associated to partial differential equations involving that operator, such as the Helmholtz equation
, the heat equation
, the Schrödinger equation
, or the wave equation
. Thus, one can hope to rephrase many arguments that involve spectral data of
into arguments that instead involve resolvents
, heat kernels
, Schrödinger propagators
, or wave propagators
, or involve the PDE more directly (e.g. applying integration by parts and energy methods to solutions of such PDE). This is certainly done to some extent in the existing literature; resolvents and heat kernels, for instance, are often utilised. In this post, I would like to explore the possibility of reformulating spectral arguments instead using the inhomogeneous wave equation
Actually it will be a bit more convenient to normalise the Laplacian by , and look instead at the automorphic wave equation
This equation somewhat resembles a “Klein-Gordon” type equation, except that the mass is imaginary! This would lead to pathological behaviour were it not for the negative curvature, which in principle creates a spectral gap of that cancels out this factor.
The point is that the wave equation approach gives access to some nice PDE techniques, such as energy methods, Sobolev inequalities and finite speed of propagation, which are somewhat submerged in the spectral framework. The wave equation also interacts well with Poincaré series; if for instance and
are
-automorphic solutions to (15) obeying suitable decay conditions, then their Poincaré series
and
will be
-automorphic solutions to the same equation (15), basically because the Laplace-Beltrami operator commutes with translations. Because of these facts, it is possible to replicate several standard spectral theory arguments in the wave equation framework, without having to deal directly with things like the asymptotics of modified Bessel functions. The wave equation approach to automorphic theory was introduced by Faddeev and Pavlov (using the Lax-Phillips scattering theory), and developed further by by Lax and Phillips, to recover many spectral facts about the Laplacian on modular curves, such as the Weyl law and the Selberg trace formula. Here, I will illustrate this by deriving three basic applications of automorphic methods in a wave equation framework, namely
- Using the Weil bound on Kloosterman sums to derive Selberg’s 3/16 theorem on the least non-trivial eigenvalue for
on
(discussed previously here);
- Conversely, showing that Selberg’s eigenvalue conjecture (improving Selberg’s
bound to the optimal
) implies an optimal bound on (smoothed) sums of Kloosterman sums; and
- Using the same bound to obtain pointwise bounds on Poincaré series similar to the ones discussed above. (Actually, the argument here does not use the wave equation, instead it just uses the Sobolev inequality.)
This post originated from an attempt to finally learn this part of analytic number theory properly, and to see if I could use a PDE-based perspective to understand it better. Ultimately, this is not that dramatic a depature from the standard approach to this subject, but I found it useful to think of things in this fashion, probably due to my existing background in PDE.
I thank Bill Duke and Ben Green for helpful discussions. My primary reference for this theory was Chapters 15, 16, and 21 of Iwaniec and Kowalski.
— 1. Selberg’s theorem —
We begin with a proof of the following celebrated result of Selberg:
Theorem 1 Let
be a natural number. Then every eigenvalue of
on
(the mean zero functions on
) is at least
.
One can show that has only pure point spectrum below
on
(see this previous blog post for more discussion). Thus, this theorem shows that the spectrum of
on
is contained in
.
We now prove this theorem. Suppose this were not the case, then we have a non-zero eigenfunction of
in
with eigenvalue
for some
; we may assume
to be real-valued, and by elliptic regularity it is smooth (on
). If it is constant in the horizontal variable, thus
, then by the
-automorphic nature of
it is easy to see that
is globally constant, contradicting the fact that it is mean zero but not identically zero. Thus it is not identically constant in the horizontal variable. By Fourier analysis on the cylinder
, one can then find a
-automorphic function
of the form
for some non-zero integer
which has a non-zero inner product with
on
, where
is a smooth compactly supported function.
Now we evolve by the wave equation
to obtain a smooth function such that
and
; the existence (and uniqueness) of such a solution to this initial value problem can be established by standard wave equation methods (e.g. parametrices and energy estimates), or by the spectral theory of the Laplacian. (One can also solve for
explicitly in terms of modified Bessel functions, but we will not need to do so here, which is one of the main points of using the wave equation method.) Since the initial data
obeyed the translation symmetry
for all
and
, we see (from the uniqueness theory and translation invariance of the wave equation) that
also obeys this symmetry; in particular
is
-automorphic for all times
. By finite speed of propagation,
remains compactly supported in
for all time
, in fact for positive time it will lie in the strip
, where we allow the implied constants to depend on the initial data
.
Taking the inner product of with the eigenfunction
on
, differentiating under the integral sign, and integrating by parts, we see that
Since is initially non-zero with zero velocity, we conclude from solving the ODE that
is a non-zero multiple of
. In particular, it grows like
as
. Using the unfolding identity (6) to write
and then using the Cauchy-Schwarz inequality, we conclude that
as , where we allow implied constants to depend on
.
We complement this lower bound with slightly crude upper bound in which we are willing to lose some powers of . We have already seen that
is supported in the strip
. Compactly supported solutions to (16) on the cylinder
conserve the energy
In particular, this quantity is for all time (recall we allow implied constants to depend on
). From Hardy’s inequality, the quantity
is non-negative. Discarding this term and using , and using the fact that
is non-zero, we arrive at the bounds
and
(We allow implied constants to depend on , but not on
.) From the fundamental theorem of calculus and Minkowski’s inequality in
, the latter inequality implies that
for , which on combining with the former inequality gives
The function also obeys the wave equation (16), so a similar argument gives
Applying a Sobolev inequality on unit squares (for ) or on squares of length comparable to
(for
) we conclude the pointwise estimates
for and
for . In particular, we write
, we have the somewhat crude estimates
for all and
. (One can do better than this, particularly for large
, but this bound will suffice for us.)
By repeating the analysis of (13) at the start of this post, we see that the quantity
can be expressed as
where
Since is supported on
and is bounded by
, the integral
is
for
. We also see that
vanishes unless
(otherwise
and
cannot simultaneously be
, and for such values of
, we have the triangle inequality bound
Evaluating the integral and then the
integral, we arrive at
and so we can bound (18) (ignoring any potential cancellation in ) by
Now we use the Weil bound for Kloosterman sums, which gives
(see e.g. this previous post for a discussion of this bound) to arrive at the bound
as . Comparing this with (17) we obtain a contradiction as
since we have
, and the claim follows.
Remark 2 It was conjectured by Linnik that
as
for any fixed
; this, when combined with a more refined analysis of the above type, implies the Selberg eigenvalue conjecture that all eigenvalues of
on
are at least
.
— 2. Consequences of Selberg’s conjecture —
In the previous section we saw how bounds on Kloosterman sums gave rise to lower bounds on eigenvalues of the Laplacian. It turns out that this implication is reversible. The simplest case (at least from the perspective of wave equation methods) is when Selberg’s eigenvalue conjecture is true, so that the Laplacian on has spectrum in
. Equivalently, one has the inequality
for all (interpreting derivatives in a distributional sense if necessary). Integrating by parts, this shows that
for all , where the gradient
and its magnitude
are computed using the Riemannian metric in
.
Now suppose one has a smooth, compactly supported in space solution to the inhomogeneous wave equation
for some forcing term which is also smooth and compactly supported in space. We assume that
has mean zero for all
. Introducing the energy
which is non-negative thanks to (19) and integrating by parts, we obtain the energy identity
and hence by Cauchy-Schwarz
and hence
(in a distributional sense at least), giving rise to the energy inequality
We can lift this inequality to the cylinder , concluding that for any smooth, compactly supported in space solution
to the inhomogeneous equation
for some forcing term which is also smooth and compactly supported in space, with
mean zero for all time, we have the energy inequality
One can use this inequality to analyse the norm of Poincaré series by testing on various functions
(and working out
using (20)). Suppose for instance that
is a fixed natural number, and
is a smooth compactly supported function. We consider the traveling wave
given by the formula
where is the primitive of
; the point is that this is an approximate solution to the homogeneous wave equation, particularly at small values of
. Clearly
is compactly supported with mean zero for
, in the region
(we allow implied constants to depend on
but not on
). In the region
,
and its first derivatives are
, giving a contribution of
to the energy
(note that the shifts of the region
by
have bounded overlap). In particular we have
and thus by the energy inequality (using only the portion of the energy)
for , where
Clearly is supported on the region
. For
, one can compute that
, giving a contribution of
to the right-hand side. When
is much less than
but much larger than
, we have
, which after some calculation yields
. As this decays so quickly as
, one can compute (using for instance the expansion (14) of (13) and crude estimates, ignoring all cancellation) that this contributes a total of
to the right-hand side also. Finally one has to deal with the region
, but
is much less than
. Here,
is equal to
, and
is equal to
, which after some computation makes
equal to
. Again, one can compute the contribution of this term to the energy inequality to be
. We conclude that
Applying the expansion (14) of (13), we conclude that
where
The expression is only non-zero when
, and the integrand is only non-zero when
and
, which makes the phase
of size
. For
much smaller than
, the phase is thus largely irrelevant and the quantity
is roughly comparable to
for
. As such, the bound (21) can be viewed as a smoothed out version of the estimate
which is basically Linnik’s conjecture, mentioned in Remark 2. One can make this connection between Selberg’s eigenvalue conjecture and Linnik’s conjecture more precise: see Section 16.6 of Iwaniec and Kowalski, which goes through modified Bessel functions rather than through wave equation methods.
— 3. Pointwise bounds on Poincaré series —
The formula (14) for (13) allows one to compute norms of Poincaré series. By using Sobolev embedding, one can then obtain pointwise control on such Poincaré series, as long as one stays away from the cusps. For instance, suppose we are interested in evaluating a Poincaré series
at a point of the form
for some
. From the Sobolev inequality we have
for any smooth function , and thus by translation
The ball meets only boundedly many translates of the standard fundamental domain of
, and hence
does too. Since
is a subgroup of
, we conclude that
meets only boundedly many translates of a fundamental domain for
. In particular, we obtain the Sobolev inequality
for any smooth -automorphic function
. This estimate is unfortunately a little inefficient when
is large, since the ball
has area comparable to one, whereas the quotient space
has area roughly comparable to
, so that one is conceding quite a bit by replacing the ball by the quotient space. Nevertheless this estimate is still useful enough to give some good results. We illustrate this by proving the estimate
for with
coprime to
, where
is a fixed smooth function supported in, say,
(and implied constants are allowed to depend on
), and the asymptotic notation is with regard to the limit
. This type of estimate (appearing for instance (in a stronger form) in this paper of Duke, Friedlander, and Iwaniec; see also Proposition 21.10 of Iwaniec and Kowalski.) establishes some equidistribution of the square roots
as
varies (while staying comparable to
). For comparison, crude estimates (ignoring the cancellation in the phase
) give a bound of
, so the bound (23) is non-trivial whenever
is significantly smaller than
. Estimates such as (23) are also useful for getting good error terms in the asymptotics for the expression (10), as was first done by Hooley.
One can write (23) in terms of Poincaré series much as was done for (10). Using the fact that the discriminant has class number one as before, we see that for every positive
and
with
, we can find an element
of
such that
has imaginary part
and real part
modulo one (thus,
and
); this element
is unique up to left translation by
. We can thus write the left-hand side of (23) as
where
and are the bottom two entries of the matrix
(determined up to sign). The condition
implies (since
must be coprime) that
are coprime to
with
for some
with
; conversely, if
obey such a condition then
. The number of such
is at most
. Thus it suffices to show that
for each such .
The constraint constrains
to a single right coset of
. Thus the left-hand side can be written as
which is just . Applying (22) (and interchanging the Poincaré series and the Laplacian), it thus suffices to show that
We can compute
where
By hypothesis, the coefficient is bounded, and so
has all derivatives bounded while remaining supported in
. Because of this, the arguments used to establish (24) can be adapted without difficulty to establish (25).
Using the expansion (14) of (13), we can write the left-hand side of (24) as
where
The first term can be computed to give a contribution of , so it suffices to show that
The quantity is vanishing unless
. In that case, the integrand vanishes unless
and
, so by the triangle inequality we have
. So the left-hand side of (26) is bounded by
By the Weil bound for Kloosterman sums, we have , so on factoring out
from
we can bound the previous expression by
and the claim follows.
Remark 3 By using improvements to Selberg’s 3/16 theorem (such as the result of Kim and Sarnak improving this fraction to
) one can improve the second term in the right-hand side of (23) slightly.

19 comments
Comments feed for this article
16 August, 2015 at 12:58 am
Asaf
Dear Prof. Tao,
Do you feel/think that there are genuine advantages using those PDE approaches over the usual representation-theoretical approach? For obvious one con, you don’t clearly ”see” Hecke operators here.
For example, if I’m not mistaken, (17) is equivalent to some main-term analysis of the fundamental solution (see Iwaniec’s book about spectral methods where he treats the automorphic Green’s function in full detail).
P.S. I believe the first systematic treatment of that kind of analysis involved with PDEs was done in the Lax-Phillips book.
16 August, 2015 at 7:49 am
Terence Tao
A great question! All the PDE arguments here are “L^2-based” and as such can be easily converted to their representation-theoretic counterparts through the spectral theorem. (Indeed, the way I found these arguments was starting with the traditional arguments and rewriting them in terms of wave propagators.) The main (but minor) benefits when doing so is that one does not need to work with asymptotics of modified Bessel functions, and also one does not need to pay all that much attention to the distinction between the continuous and pure point components of the spectrum. But this was never the deepest part of the theory.
My (somewhat vague) hope is that there are more advanced L^p PDE methods for p not equal to 2 that are easier to see in terms of PDE such as the wave equation than they would be in terms of eigenfunctions. For instance, for the wave equation there are Strichartz estimates and Morawetz estimates, which give non-trivial L^p estimates for such solutions on domains such as hyperbolic space. Unfortunately when passing to modular curves it seems that such estimates are nontrivial only for short times t, which is not the regime of interest in analytic number theory (this is part of a much more general problem that the wave equation on compact or nearly compact manifolds is notoriously difficult to control for long times).
To me, perhaps the main benefit is psychological; I feel very comfortable with the wave equation, but did not previously have much intuition for cusp forms, Eisenstein series, or the modified Bessel function, and so I find automorphic forms methods much more approachable now.
p.s. I can’t believe I missed the connection to the Lax-Phillips scattering theory, which of course uses the exact same wave equation! I’ve modified the post accordingly.
17 August, 2015 at 9:35 am
lqpman
Actually, the application of scattering theory of the wave equation in hyperbolic space to the theory of automorphic forms was originally due to Faddeev and Pavlov in 1972, after a remark due to Gel’fand in his 1962 ICM talk. The book by Lax and Phillips “Scattering Theory for Automorphic Functions” (Princeton, 1976) was to a great extent motivated by this work.
[Thanks for the reference – I’ve adjusted the text accordingly – T.]
16 August, 2015 at 5:30 am
Spectra of Modular Surfaces I | Fight with Infinity
[…] 回到对的讨论。我们将另辟新章讨论作为算术量子混沌系统的及其高能渐进。在低能端,数论学家感兴趣的主要是第一特征值估计: (Selberg 1/4猜想),即大于0的离散谱完全落在连续谱中。 (Selberg 1/4猜想,几何分析形式)满足,梯度估计 成立。 不难证明1/4是最优的:时,的尖点谱在中趋于稠密。事实上,对于不可约2维偶Galois表示,若相应的Artin L-函数是整函数(即满足Artin猜想),则通过Langlands对应原理,它给出上的Maass尖点形式,是的导子。 对于,通过简单的推理即可得到强得多的下界,例如 (Vignéras). 对于一般的,Selberg证明了,对这个结果感兴趣的读者不妨参考陶哲轩的博文。 […]
17 August, 2015 at 1:40 am
Anonymous
The remark below theorem 1 (that the spectrum should be contained in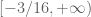 ) is not sufficiently clear.
) is not sufficiently clear.
[Sign error corrected, thanks – T.]
18 August, 2015 at 8:13 am
lqpman
Dear Prof. Tao,
there is a reference with no links to a previous post of yours in the beginning of the paragraph just before the inhomogeneous wave equation, i.e. the formula preceding the automorphic wave equation (15).
I’d also like to remark that the real (time) line times the Poincaré half-plane is (a piece of) the three-dimensional anti-de Sitter space-time with scalar curvature -2, hence equation (15) in
is (a piece of) the three-dimensional anti-de Sitter space-time with scalar curvature -2, hence equation (15) in  is the conformally coupled wave equation in this space-time. This raises the following question: according to the classification of the self-adjoint extensions of the spatial part of the Klein-Gordon operator in anti-de Sitter space-time (see e.g. the paper by A. Ishibashi and R. M. Wald, Class. Quantum Grav. 21 (2003) 2981-3013), one should have a 1-parameter family of boundary conditions at conformal infinity (corresponding to the time line times the boundary of the upper half-plane) for conformal coupling and mass zero, due to the fact that
is the conformally coupled wave equation in this space-time. This raises the following question: according to the classification of the self-adjoint extensions of the spatial part of the Klein-Gordon operator in anti-de Sitter space-time (see e.g. the paper by A. Ishibashi and R. M. Wald, Class. Quantum Grav. 21 (2003) 2981-3013), one should have a 1-parameter family of boundary conditions at conformal infinity (corresponding to the time line times the boundary of the upper half-plane) for conformal coupling and mass zero, due to the fact that 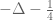 has deficiency indices (1,1). Which boundary condition is the one chosen in the above analysis?
has deficiency indices (1,1). Which boundary condition is the one chosen in the above analysis?
Finally, does this choice of boundary conditions affect the decay of solutions of the automorphic wave equation? It is known, for instance, that solutions of the conformally coupled wave equation in anti-de Sitter space-time with Dirichlet boundary conditions at conformal infinity do not decay at all for large times since the solutions are always refocused back after dispersing for a while.
18 August, 2015 at 9:50 am
Terence Tao
Thanks for pointing out the missing link, which I’ve now put in.
I’ve not thought about self-adjoint extensions of hyperbolic operators such as the Klein-Gordon operator or d’Lambertian before; I’m not sure it is directly relevant for the above analysis as we are not trying to deploy a functional calculus for d’Lambertian or Klein-Gordon operators such as , but are instead trying to use a functional calculus for the automorphic Laplacian
, but are instead trying to use a functional calculus for the automorphic Laplacian 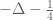 . In particular, solutions to the automorphic wave equation would probably not lie in the domain for the Klein-Gordon operator, much as solutions to the Poisson equation
. In particular, solutions to the automorphic wave equation would probably not lie in the domain for the Klein-Gordon operator, much as solutions to the Poisson equation 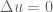 usually do not lie in the domain of the Laplacian. Nevertheless there should clearly be some relationship between the two functional calculi, but I would have to think further to discern the precise link. Note also that conformal compactification does not seem to play well with
usually do not lie in the domain of the Laplacian. Nevertheless there should clearly be some relationship between the two functional calculi, but I would have to think further to discern the precise link. Note also that conformal compactification does not seem to play well with 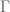 -automorphy for various discrete groups, for instance there doesn’t appear to be a good conformal compactification of the partially periodic spacetime
-automorphy for various discrete groups, for instance there doesn’t appear to be a good conformal compactification of the partially periodic spacetime 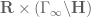 , so these sorts of techniques may not be so relevant for the number theory applications (though they are presumably useful for understanding the automorphic wave equation on hyperbolic space when not restricting to
, so these sorts of techniques may not be so relevant for the number theory applications (though they are presumably useful for understanding the automorphic wave equation on hyperbolic space when not restricting to 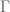 -automorphic solutions).
-automorphic solutions).
18 August, 2015 at 3:38 pm
lqpman
Actually, I was referring to self-adjoint extensions of the “spatial” part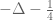 . It is this operator on
. It is this operator on  (with domain
(with domain 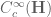 , I had forgotten to mention) which has deficiency indices (1,1), according to the paper of Ishibashi and Wald I have cited above. Sorry for not being sufficiently clear before.
, I had forgotten to mention) which has deficiency indices (1,1), according to the paper of Ishibashi and Wald I have cited above. Sorry for not being sufficiently clear before.
18 August, 2015 at 8:39 pm
Terence Tao
Hmm, when I calculate the wave equation for anti de Sitter space I seem to get a different wave equation than (15). If I take the coordinates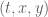 with
with 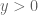 and metric
and metric 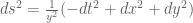 , I seem to get a d’Lambertian of
, I seem to get a d’Lambertian of 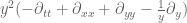 whereas the differential operator for (15) is
whereas the differential operator for (15) is 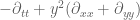 . I may have made a sign error or two but I doubt that the two operators are closely related.
. I may have made a sign error or two but I doubt that the two operators are closely related.
One can use standard energy methods to show that the equation (15) is globally hyperbolic, with the Cauchy problem being well posed in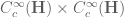 , so there should be a unique self-adjoint extension (zero deficiency indices) for this operator.
, so there should be a unique self-adjoint extension (zero deficiency indices) for this operator.
19 August, 2015 at 7:30 am
lqpman
Oops, you’re right. I forgot the factor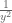 multiplying
multiplying 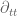 . This factor changes everything, since anti-de Sitter space-time is not globally hyperbolic.
. This factor changes everything, since anti-de Sitter space-time is not globally hyperbolic.
OK, this sort of answers my question by invalidation. A bit embarrassing, but I learned something. Thanks!
19 August, 2015 at 7:40 am
Terence Tao
I believe the relevant spacetime for (15) is the spacetime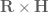 with metric
with metric 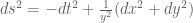 , which differs from the anti de Sitter metric by not having the
, which differs from the anti de Sitter metric by not having the 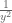 factor multiplying the
factor multiplying the  term.
term.
19 August, 2015 at 7:47 am
lqpman
Indeed. Which is, of course, globally hyperbolic since it is ultra-static and the spatial factor is a complete Riemannian manifold.
is a complete Riemannian manifold.
20 August, 2015 at 11:34 am
John Mangual
Why do automorphic forms relate to special relativity?
22 August, 2015 at 7:28 pm
Wilde
‘which (up to a harmless sign) is exatly the representation . . . ‘
Typo here.
Mr Tao: I’ve got an unrelated question for you and would be grateful to you if you answered it. Have you ever perused string-theory papers and been able to understand moderately or extremely well what they’re discussing, or, because those are papers in theoretical physics, are they speaking a totally different language than the mathematical one you know?
[Corrected, thanks. I’ve looked at some QFT papers, and intend to learn that material in depth at some point (there are a number of treatments of these topics from a mathematical perspective), but have not read any of the string theory literature (other than popular expositions, of course). -T.]
23 August, 2015 at 8:10 am
hashtag
I found two relevant references: One is a talk by Terence Tao in March 2015 on “Can the Navier-Stokes Equations Blow Up in Finite Time?” (https://www.youtube.com/watch?v=DgmuGqeRTto“), which is a wonderful summary of all these ideas – understandable for non-experts as me :-)
Another one is a NYT article from July 2015: http://www.nytimes.com/2015/07/26/magazine/the-singular-mind-of-terry-tao.html?_r=1
24 August, 2015 at 8:23 am
Anthony Quas
I guess (line 3) that the projective speciexetal groups are the projective special groups? (you do write PSL one line later, but the word “speciexetal” sounded almost mathematical enough that this could have been a class of groups I was unaware of).
[Corrected, thanks – no idea where that typo came from, though. -T.]
24 March, 2016 at 5:39 am
MrCactu5 (@MonsieurCactus)
For a long time I confused the Schrödinger equation, the heat equation and the wave equation. Since in the textbook they all use Fourier series.
Harmonic analysis seems intimately tied to the eigenfunctions of the Laplacian . In the case of a circle or sphere or many symmetric spaces these well-understood (ahem… on Wikipedia). I assumed analysis on
. In the case of a circle or sphere or many symmetric spaces these well-understood (ahem… on Wikipedia). I assumed analysis on  should play out identically and indeed you augment Fourier analysis on the line to Harmonic Analysis on the fundamental domain in some kind of way but the result is very complicated.
should play out identically and indeed you augment Fourier analysis on the line to Harmonic Analysis on the fundamental domain in some kind of way but the result is very complicated.
Can you develop representation theory or harmonic from other PDE?
I am not sure there’s even any point to asking this question until I re-read my analysis textbooks.
30 August, 2016 at 4:09 pm
Heuristic computation of correlations of the divisor function | What's new
[…] on error terms. A more modern approach proceeds using automorphic form methods, as discussed in this previous post. A third approach, which unfortunately is only heuristic at the current level of technology, is to […]
22 February, 2019 at 2:06 pm
Adeles and Automorphic Forms – Tlapohuayotl
[…] group, the actions, but it is cool how this is related to hyperbolic equations and pde. There is a post on Terry Tao’s blog on this and how a background in PDE can overlap with this aspect of […]