I’ve just uploaded to the arXiv the D.H.J. Polymath paper “Variants of the Selberg sieve, and bounded intervals containing many primes“, which is the second paper to be produced from the Polymath8 project (the first one being discussed here). We’ll refer to this latter paper here as the Polymath8b paper, and the former as the Polymath8a paper. As with Polymath8a, the Polymath8b paper is concerned with the smallest asymptotic prime gap
where 
denotes the 
prime, as well as the more general quantities
In the breakthrough paper of Goldston, Pintz, and Yildirim, the bound 
was obtained under the strong hypothesis of the Elliott-Halberstam conjecture. An unconditional bound on 
, however, remained elusive until the celebrated work of Zhang last year, who showed that
The Polymath8a paper then improved this to 
. After that, Maynard introduced a new multidimensional Selberg sieve argument that gave the substantial improvement
unconditionally, and 
on the Elliott-Halberstam conjecture; furthermore, bounds on 
for higher 
were obtained for the first time, and specifically that 
for all 
, with the improvements 
and 
on the Elliott-Halberstam conjecture. (I had independently discovered the multidimensional sieve idea, although I did not obtain Maynard’s specific numerical results, and my asymptotic bounds were a bit weaker.)
In Polymath8b, we obtain some further improvements. Unconditionally, we have 
and 
, together with some explicit bounds on 
; on the Elliott-Halberstam conjecture we have 
and some numerical improvements to the bounds; and assuming the generalised Elliott-Halberstam conjecture we have the bound 
, which is best possible from sieve-theoretic methods thanks to the parity problem obstruction.
There were a variety of methods used to establish these results. Maynard’s paper obtained a criterion for bounding which reduced to finding a good solution to a certain multidimensional variational problem. When the dimension parameter 
was relatively small (e.g. 
), we were able to obtain good numerical solutions both by continuing the method of Maynard (using a basis of symmetric polynomials), or by using a Krylov iteration scheme. For large , we refined the asymptotics and obtained near-optimal solutions of the variational problem. For the bounds, we extended the reach of the multidimensional Selberg sieve (particularly under the assumption of the generalised Elliott-Halberstam conjecture) by allowing the function 
in the multidimensional variational problem to extend to a larger region of space than was previously admissible, albeit with some tricky new constraints on (and penalties in the variational problem). This required some unusual sieve-theoretic manipulations, notably an “epsilon trick”, ultimately relying on the elementary inequality 
, that allowed one to get non-trivial lower bounds for sums such as 
even if the sum 
had no non-trivial estimates available; and a way to estimate divisor sums such as 
even if 
was permitted to be comparable to or even exceed 
, by using the fundamental theorem of arithmetic to factorise 
(after restricting to the case when is almost prime). I hope that these sieve-theoretic tricks will be useful in future work in the subject.
With this paper, the Polymath8 project is almost complete; there is still a little bit of scope to push our methods further and get some modest improvement for instance to the bound, but this would require a substantial amount of effort, and it is probably best to instead wait for some new breakthrough in the subject to come along. One final task we are performing is to write up a retrospective article on both the 8a and 8b experiences, an incomplete writeup of which can be found here. If anyone wishes to contribute some commentary on these projects (whether you were an active contributor, an occasional contributor, or a silent “lurker” in the online discussion), please feel free to do so in the comments to this post.
Like this:
Like Loading...
Related
110 comments
Comments feed for this article
20 July, 2014 at 9:58 pm
David Roberts
In the paragraph starting “In Polymath8b, we obtain some further improvements.”, need to put brackets on the exponent in the asymptotic H_m bound to get ‘(4-24/181)m’, not ‘4-24m/181’.
[Corrected, thanks – T.]
20 July, 2014 at 10:05 pm
Anonymous
Introduction: Remove either “
denote the quantity” from the first line or “
” from the formula.
20 July, 2014 at 11:27 pm
foobar
Couple purely formatting-related notes on the retrospective: footnote 3 on page 3 doesn’t fit on the page (and lacks http:// on the link), and link at “A database had been set up at math.mit.edu/primegaps/” (page 8) similarly lacks http://, and has a strange symbol on middle of it (I assume it should be a tilde).
[Corrected, thanks – T.]
21 July, 2014 at 5:43 pm
Blake Stacey
This is where the \url{} command in the hyperref package comes in handy; it has a decent ability at breaking lines in the right places.
21 July, 2014 at 12:17 am
Avi Levy
Last sentence of second to last paragraph: “I hope that these sieve-theoretic tricks will be future in other work in the subject.”
Perhaps you meant “useful in future work”?
[Corrected, thanks – T.]
21 July, 2014 at 9:38 am
Eytan Paldi
It is still possible that
(in fact, as already commented by Ignace, repeated Shanks extrapolations indicate that 
seems to be in the interval ![[4.0004, 4.00004]](https://s0.wp.com/latex.php?latex=%5B4.0004%2C+4.00004%5D&bg=ffffff&fg=545454&s=0 "[4.0004, 4.00004]")
). The problem is that the maximal degree of the polynomials in the Krylov bounding method should be sufficiently large (apparently 70-90 – instead of the current 50) in order to rigorously show that.
If true, this should improve (under EH) theorem 1.4(vii) from
to 
. (with corresponding improvements in theorems 3.2(vii) and 3.9(vii)).
(this possible improvement may be added to the remarks in section 9).
[A brief note to this effect added – T.]
21 July, 2014 at 12:30 pm
James Maynard
I’d happily write a brief piece for the retrospective if you would like, although I think my thoughts might be very similar to those of Pace, and so I’m equally happy to leave his comments as representative of mine as well.
I think there is a small typo on the exponent for large
; if 
then I get an exponent 
rather than 
(on line 13 of page 14 I think 
has accidentally become 
, and this affects the exponent in the next equation, in the abstract, in Theorem 1.4 and in Theorem 3.2)
[Corrected, thanks. Given your role in prior developments, I think a separate piece from you would definitely be interesting, even if it echoes other comments. -T.]
21 July, 2014 at 5:48 pm
Blake Stacey
This sentence appears to be missing a word: “Initially, I was preoccupied with other research projects, and felt content to let the rest of the analytic number theory digest the result”.
Perhaps insert “community” in between “theory” and “digest”.
[Corrected, thanks – T.]
21 July, 2014 at 10:39 pm
Polymath 8 – a Success! | Combinatorics and more
[…] the Selberg sieve, and bounded intervals containing many primes“, is now on the arXiv. See also this post on Terry Tao’s […]
22 July, 2014 at 1:52 am
Anonymous
Typographical comment: For the seventeen million in the third math expression, you can avoid the space after the commas by inclosing these in brackets;
.
[Corrected,thanks – T.]
22 July, 2014 at 1:53 am
Anonymous
This also applies to $4{,}680$ in the very next line. :)
23 July, 2014 at 4:16 am
Anonymous
One thing that I usually do to get around this problem is \usepackage{icomma}.
23 July, 2014 at 10:25 pm
Anonymous
Perhaps best to omit the comma altogether for four digit numbers.
22 July, 2014 at 7:47 am
Amancio Perez
Profesor Tao.
$ latex \forall (p_{n+1} – p)\leq 6 $
DEMONSTRATION
with a = ( 0;1 ;2;3;4;5;6;7;8…….
); there is always a pair of primes.
Each of these equalities is a Prime Number provided they are not multiples of any of the following numbers respectively ( 3; 5; 7; 11; 13; 17; 19; 23; 29; 31;37;43).
These equation published are of Andri Lopez; personally the informe to you the day 6 of June by email.
Profesor Tao, asap check equations and will have solved the problem.
29 July, 2014 at 4:46 am
anonymous
Oops. First equation for a=10000011 has “p(n+1)” = 300000359 = 163 x 1840493.
30 July, 2014 at 7:57 am
anonymous
These are just re-statement of Dirichlet’s theorem.
http://en.wikipedia.org/wiki/Dirichlet%27s_theorem_on_arithmetic_progressions
22 July, 2014 at 8:16 am
Eytan Paldi
Lemma 3.4 may be slightly improved as follows:
Let
defined as in lemma 3.4.
be the set of indices ![n \in [x. 2 x] , n=b(W)](https://s0.wp.com/latex.php?latex=n+%5Cin+%5Bx.+2+x%5D+%2C+n%3Db%28W%29&bg=ffffff&fg=545454&s=0 "n \in [x. 2 x] , n=b(W)")
Let
Let
be defined for each 
as the number of indices 
for which 
is prime.
Denote by
the weighted average (wrt the normalized weights 
) of 
over 
, i.e.
(1) $ latex m_{av} := \sum_{n \in S} w_n m(n)
Then
(2)
Remarks:
1. Since (obviously)
, this implies lemma 3.4 (i.e. (2) holds with 
in the LHS).
2. Clearly, this is equivalent to lemma 3.4 if and only if
is constant over 
. So if there is some way to lower bound the difference 
it may lead to some improvements for 
.
22 July, 2014 at 1:42 pm
Eytan Paldi
In the Polymath8b paper, it seems that a factor
is missing in the RHS of (77).
[Corrected – T.]
22 July, 2014 at 1:57 pm
Eytan Paldi
In the Polymath8b paper, page 34 line 2, “(77)” should be “(76)”.
[Corrected – T.]
25 July, 2014 at 1:16 pm
vznvzn
awesome work. suggest this following book by Nielsen be cited somewhere. it specifically cites polymath as paradigm shifting and (admittedly somewhat grandiosely, yet with major justification) considers that cyberspatial collaboration is helping facilitate a scientific revolution roughly in scale to the age of enlightenment a half-millenium later. few seem to have read it or digested its implications. Reinventing Discovery: The New Era of Networked Science. if a sequel was written (and presumably one will be by someone), Zhangs proof & polymath improvements would surely be in it.
25 July, 2014 at 1:27 pm
vznvzn
(oops) 2nd thought another quick point. at various stages in the polymath attack, empirical approaches ie computers/ algorithms were used to find improved sieves. this is a relatively well-concealed fact looking at accounts of the proceedings. would like to learn more about this. you might decide the paper might not be the place for that, but it would be great if someone could document this further somewhere. & ps some commentary & many links on zhang incl much media coverage, interview etc
25 July, 2014 at 3:36 pm
Eytan Paldi
In Polymath8b paper, it seems (according to (16)), that the RHS of (20) should be
(instead of 
) for prime 
. (due to its divisors 
).
[Clarified -T.]
25 July, 2014 at 3:51 pm
Eytan Paldi
I can see now that for
the second term vanishes!
may be added in the line below (20)).
(perhaps this condition on
26 July, 2014 at 10:21 am
Eytan Paldi
In the line below (20), “
” should be “
“.
should vanish).
(so that the second term
[Corrected, thanks – T.]
26 July, 2014 at 8:20 am
Terence Tao
RIMS has already come back with two referee reports for Polymath8b: https://www.dropbox.com/sh/j1ncthw7dwupj6a/AAANZvStKFAwvRptu00rA-ULa The corrections requested are fairly minor, I can address them myself within the next few days.
26 July, 2014 at 8:51 am
Andreas
The referee-reports of the two papers are very different. Reports of paper1 had alot of minor corrections, thus indicated that the reviewers calculated alot of the presented material. Reports for paper2 do not have any comments about the technical details at all. Paper1 had 5 or 6 independent referees looking at different sections. Paper2 had 2 reviewers for the whole content. Paper1 took many weeks; paper2 took a few days?
As a non-mathematician, I wonder what kind of reviews are more common; is the main goal of a reviewer to check the full technical results or check and help to improve the way the paper is presented? I believe, potential mistakes will be found anyway after its published and presented to the whole of experts of the field.
26 July, 2014 at 8:47 pm
Pace Nielsen
Andreas, great questions. There are a number of factors which can influence the way a referee report is created.
1. The type of journal. If the journal is geared towards presenting mathematics to largely non-mathematician audiences, then the focus is different than if the journal is devoted to short articles, which is different than a journal focused on major new results. Some journals pride themselves on quick decisions; others are meticulous about details.
2. The workload for the referee. When you know that you are one of many reviewers, but you are in charge of reviewing only one (short) section of a paper, you will take more care to check every detail (to pull your own weight, so to speak). If you are reviewing a 50+ page paper in its entirety; then you look at the broad ideas. Ultimately, the correctness of a paper is the author’s, not the referee’s, responsibility. However, referees do try to make a reasonable effort to verify results.
To give you a more personal example, I’m the type of referee who if I agree to do the job, I want to get it done quickly but also check every detail. So I give myself a month, and try to check every detail. (This is possible since most papers in my field are relatively short.) But there are some papers where it is just too much work to do that, so I check the details for a while, but may just read other parts for cohesion.
3. Editor instructions. Some journals have huge backlogs, and so editors instruct referees to be more discriminating. Most referee reports from those journals are rejections. In area-specific journals, some editors know that certain authors are “solid” but heavy on technicalities, and so may only require an estimation of the impact of the paper.
4. Style of the paper. If English is an author’s first language, there will be in many cases fewer typographical changes for the referee to recommend. Similarly, an author versed in LaTeX will make fewer bad choices in that regard. Finally, some papers even if correct are unreadable, while others, such as the polymath 8b paper, are easy to read even with a long length (just as one of the referees mentioned).
There are many other considerations. To answer your question about what is the usual format of a report; it really does depend on a large number of factors. When an article just “fits” a journal and is well written there are usually fewer recommended changes. On the other hand, if there are oddities that the authors just didn’t see, the referee might focus in on those issues and make a detailed report.
There are other types of reports than those received for the polymath 8 papers. For instance, some are:
1. Rejections with no comments from the referee.
2. Acceptance with no comments from the referee. (These are the ones I worry about the most when I get them! A serious referee should have found at least one change to recommend–that’s just the way life is; errors occur.)
3. Rejections for serious errors.
4. Serious revisions requested for badly written papers, possibly with some results having gaps.
I hope this helps.
26 July, 2014 at 8:50 pm
Pace Nielsen
That’s wonderful news! (I always like quick refereeing.) Those were both very positive reports, with some good recommendations.
29 July, 2014 at 7:11 am
Terence Tao
I’ve now implemented the corrections to 8b. I see there are still a few corrections coming in, so I’ll wait for another day or two before submitting the revised version back to RIMS (who are promising a speedy publication – so 8b may in fact end up in print slightly before 8a, which is actually not entirely uncommon, given the wide variability in publication times).
2 August, 2014 at 8:48 am
Terence Tao
I’ve now sent the revised version back to RIMS.
3 August, 2014 at 1:46 am
Eytan Paldi
It seems that the typos (mentioned in my comment from 30 July) are still in the paper.
[Oops, I somehow overlooked that comment. I’ve implemented the changes now; I won’t update the arXiv version as the changes are minor, but I may have an opportunity to implement the changes in the galley proofs for RMS. -T.]
26 July, 2014 at 12:07 pm
Eytan Paldi
In Polymath8b paper, in the fifth line of remark 3.7, it seems that “(20)” should be “(26)”.
[No; (26) only addresses the case
. (20) asserts that 
is quite large (much larger than its average value) whenever 
is non-zero. -T.]
26 July, 2014 at 12:39 pm
Eytan Paldi
In Polymath8b paper, it seems that in the LHS of (26), “
” should be “
“.
[Corrected, thanks – and now I see where the prior confusion came from. -T.]
27 July, 2014 at 2:13 am
Eytan Paldi
In Polymath8b paper, “
” should be “
” both in (8) and in the fourth line below theorem 2.8.
Also, in (21) “
” seems (slightly) better than “
“.
[Corrected, thanks – T.]
27 July, 2014 at 2:38 am
H
I think the boldface caption for the table on p.8 looks a bit strange.
Also, in the example bmc_article_2col.pdf captions are not bold.
However, I don’t understand why it gets typeset this way.
The following small example sets the first table-caption in bold and the second not in bold.
If the figure in between is removed, then both are typeset in bold.
\documentclass{bmcart}
\begin{document}
\begin{table}
\caption{Sample table title.}
\end{table}
\begin{figure}
\caption{\csentence{Sample figure title.} A short description.}
\end{figure}
\begin{table}
\caption{Sample table title.}
\end{table}
\end{document}
28 July, 2014 at 9:56 am
H
I don’t really understand the latex in bmcart.cls, but I think that every time a figure-environment is created the line
\setattribute{floatcaption}{size}{\footnotesize\sffamily\raggedright}
is run (lines 720, 734 in bmcart.cls). This affects how the caption of tables are typeset and explains the strange behavior pointed out in the small example.
Adding the row displayed above to the preamble of the latex document “fixes” the boldness-issue. However, I guess this kind of hack is not encouraged… I’m only posting this to try to explain the weirdness noted in my previous comment.
27 July, 2014 at 5:29 am
LB
Three very minor mistakes in several threads:
In Scott Morrison’s thread (http://sbseminar.wordpress.com/2013/05/30/i-just-cant-resist-there-are-infinitely-many-pairs-of-primes-at-most-59470640-apart), there is still one time written 3.5*10^7, which should be 3.5*10^6, even though this was already mentioned and corrected once (but not in the 5th paragraph).
Also, in the second thread (https://terrytao.wordpress.com/2013/06/03/the-prime-tuples-conjecture-sieve-theory-and-the-work-of-goldston-pintz-yildirim-motohashi-pintz-and-zhang/), in the Bessel differential eqaution the term d/dx^2 should be replaced by d^2/dx^2 for sure.
Third, in the Polymath 8a paper, in section “Abstract”, there is just written “gives Zhang’s theorem with H=”, without giving the value of 4,680.
27 July, 2014 at 7:35 pm
James Maynard
Good news from the referee report! Here is a draft of my thoughts for the retrospective article (feel free to edit if this is too long):
As a graduate student who had be looking at closely related problems, it was thrilling to hear of Zhang’s initial breakthrough. I didn’t participate in the subsequent Polymath 8a project, although I found myself reading several of the posts whilst studying Zhang’s work for myself. I intended to avoid working on anything too close to the Polymath project (to avoid any competition), but one day I was going back through some ideas I’d had a several months earlier on modifications of the `GPY sieve’, and I realized I could overcome the obstacles I had in my original attempt. This modification (also discovered by Tao) gave an alternative stronger approach to gaps between primes, although it didn’t produce the equidistribution results which lie at the heart of Zhang’s work. With some small numerical calculations, this allowed me to show that there were infinitely many pairs of primes which differ by at most 600, and allowed one to show the existence of many primes in bounded length intervals.
I knew the numerical bounds in my work hadn’t been fully optimized – there was some slack in my approach, and there were also several opportunities to extend the method (such as incorporating ideas from Zhang and Polymath8a, or using more careful arguments). I was therefore pleased and excited when I learnt there was the intention for a polymath 8b project which I could be part of – it was very exciting for me that there was such an interest in my work!
The style of a large collaborative project was very new to me. I had relatively little experience of research collaboration, and I was used to mainly trying out ideas alone. I certainly hadn’t fully appreciated quite how public the posts were (and how many mathematicians who were not active participants would read the comments). In some ways this was quite fortunate; not realizing the attention posts might receive made me more willing to contribute openly. I posted several ideas which were not fully thought through, some of which were rather stupid in hindsight, but some of which I believe were useful to the project (and probably more useful than posting a fully thought out idea a few days later). The atmosphere of the project certainly helped encourage such partial contributions, which I feel was a large factor in the project’s success.
It was remarkable (to me, at least) how smoothly the project went; this was partly to do with the problem having very clearly defined goals and being modular in its nature, but also due to the openness and friendliness of the participants. There seemed to be a good balance amongst the participants – some had more computational expertise, whilst others had a more theoretical background, and it was certainly useful to have both groups together for the effectiveness of the project. Much if the improvement in the unconditional bound came from extending the computations I had done initially, and it was certainly useful to have people who were rather more experienced than me with the larger computations.
I was surprised at how much time I ended up devoting to the polymath project. This was partly because the nature of the project was so compelling – there were clear numerical metrics of `progress’, and always several possible ways of obtaining small improvements, which was continually encouraging. The general enthusiasm amongst the participants (and others outside of the project) also encouraged me to get more and more involved in the project. Finally, the nature of the work also made it very suitable for working on in short bursts, which turned out to be very useful since I was travelling quite a lot whilst most of the project was underway.
I was aware that as a junior academic without a permanent position that I might ultimately not receive much credit in the eyes of hiring committees for participation in an atypical project such as the polymath, where it is difficult to gauge the merit of my contribution. In my case, the fact that the project was so closely associated with my earlier work, and the fact that I found the project so interesting made me happy to accept this (although I made a conscious effort to continue to work on other projects at the same time). This is certainly something I feel any similarly junior prospective participant should be aware of, however.
Overall, I really enjoyed the polymath experience. It was a great opportunity to work with several other mathematicians, and I feel pleased with the final results and my contribution to them.
[Added to the retrospective paper; may try to do some minor editing later. – T.]
27 July, 2014 at 8:44 pm
Pace Nielsen
Good thoughts! (By the way, with the quality of you work on multidimensional sieves, and your subsequent follow-up work, I don’t think you have much to worry about from hiring committees.)
One minor suggestion. You wrote “I had relatively little experience of research collaboration, and I was used to mainly trying out ideas alone.” I initially read “I was used to…” as something like “I was used by the polymath project to…” rather than what you meant, which was “I was more familiar with…”. You might consider changing this sentence to avoid that misreading.
28 July, 2014 at 5:13 am
Gergely Harcos
James’ nice contribution for the retrospective article encouraged me to write up mine:
“I guess I am no longer a junior mathematician, which is a bad thing, but on the good side I can perhaps add a different perspective on my participation in the PolyMath8 project.
Last year I applied for some serious grants, and it was on the same day when I learned that my proposals would be rejected. This was quite discouraging, and I felt as I needed to take some break from my main line of research. Around the same time, Zhang’s exciting paper came out, and shortly after Terry Tao initiated a public reading seminar on his blog that later turned into the PolyMath8 project. I was already familiar with the earlier breakthrough by Goldston-Pintz-Yildirim, in fact I have incorporated it in my courses at Central European University and advised some students in related topics. I have always found this part of number theory very beautiful, although my research interests have been elsewhere. Following Terry’s clean and insightful blog entries and the accompanying comments served for me two different purposes initially. First, I hoped to understand the new developments in a field that I found appealing. Second, I hoped to get a change of air in mathematics for the reasons explained above.
The PolyMath8 project developed at blazing speed, and my initial goal was simply to catch up and read everything posted on the blog. This was quite challenging, because I am rather slow and prefer to check every line carefully, but at least I could serve as an early referee for the project. As a bonus, I got some ideas how to improve certain points in an argument already posted. In short, the PolyMath8 project helped me to get going and feel myself useful, and participating was a lot of fun. At one point I embarrassed myself by posting several different “proofs” to an improved inequality that I conjectured, only to find out later that the claim was false. All this is recorded and preserved in the blog, but I do not regret it as it was honest and reflects the way mathematics is done. We try and we often fail.
It was also very interesting how my colleagues reacted. Some thought that one should not devote too much effort to a paper published under a pseudoname, but in fact my participation here got far more attention than elsewhere. For a couple of months the first question I was asked was about the current record on prime gaps. Another benefit of a PolyMath project is that there is no pressure on the participants, one is free to join for a while then leave, and ignorance is normal as in a mathematical conversation.”
[Added to the retrospective paper; may try to do some minor editing later. – T.]
28 July, 2014 at 7:27 am
Eytan Paldi
In tables 4, 5 (pages 77, 78) of Polymath8b paper, “Best known” seems to be a better description than “Best result”.
[Corrected, thanks – T.]
28 July, 2014 at 1:59 pm
Eytan Paldi
Table 5 should also be corrected.
[Done, thanks – T.]
28 July, 2014 at 4:27 pm
H
Some displayed math is left-aligned and some is centered, is this intentional?
(I think $$-math is centered and \begin{equation}-math is left-aligned.)
[This appears to be the journal house style; I presume that if there is an issue they will raise it in the galley proof stage. -T.]
29 July, 2014 at 1:19 am
Eytan Paldi
In the abstract of Polymath8b paper, the exponent of the unconditional asymptotic bound on
should be corrected (to that of theorem 1.4(vi)).
[Corrected, thanks – T.]
29 July, 2014 at 2:42 am
Eytan Paldi
Some remarks on the polymath8b paper:
1. In the abstract, from the disjunction formulation it seems (unlike as in theorem 1.5 formulation) that it is an “exclusive or” type (i.e. exactly one possibility holds).
2. In section 1.1, theorem 3.2 is not mentioned. (perhaps, table 1 -describing its dependence on other theorems – may be mentioned here.)
Also in section 1.1, “gives Theorem 1.4” seems better than “to give Theorem 1.4”.
[Corrected, thanks – T.]
30 July, 2014 at 4:50 am
Eytan Paldi
Corrections for the Polymath8b paper:
1. Page 4: line 7 of section 1.1, “in 4” should be “in Section 4”.
2. Page 6: in Claim 2.6, the condition
(for fixed 
) may be added.
3. Page 8: in Theorem 3.2. "
" (four places !) should be "
".
4. Page 28: in (63) and in lines 2, 4, 6. 7 above (63), "
" should be "
".
5. Page 29: in the first two summations, "
" should be "
".
6, Page 38: in the first three summations, the summands should be inside parentheses.
7. Page 39: in the first summation, the summands should be inside parenheses.
8. Page 41: in the line below (92), "of intervals" should be "on intervals".
9. Page 44: in proposition 6.5, "
" should be "
".
10. In the proof of Theorem 6.7, it seems helpful to remark (at appropriate place) that the convention used for the expectation operator is that (without parentheses) it applied to the whole expression to its right.
11. Page 58: In the sixth line below the expression for
, "maximize" should be "maximizes" and "quantity
" should be "quantity 
".
[Belatedly corrected, thanks – T.]
3 August, 2014 at 4:49 am
Eytan Paldi
There are still some typos (using the same corrections numbering):
2. Page 6: in the line above Claim 2.6, “
” (inside the inequality) should be “
“.
3. Page 8: in theorem 3.2, “
” (appearing twice in the second line below (vi), and twice in the second line below (xi)) should be “
“.
is consistently reserved to be the parameter for the claims EH[.] and GEH[.]).
(as I understand,
9. Page 44: in proposition 6.5, “
" should (obviously) be "
".
[Corrected, thanks – T.]
13 August, 2014 at 9:47 am
Eytan Paldi
There is still a typo (see my comment above)
Page 6: in the line above claim 2.6, “
" should be "
" .
Also, in page 36, two lines above the proof of theorem 3.10, it seems that "
" (in the summation) should be "
".
[Corrected, thanks – T.]
30 July, 2014 at 11:25 pm
David Roberts
My 2 cents for the retrospective.
“I saw the announcement of Zhang’s talk on Peter Woit’s blog, and posted on Google+ (13 May 2013) about the twin prime problem, prime gaps more generally and about Zhang’s talk and how big a deal it was. This post received much attention (more than I would have expected) and over the course of Polymath 8, and the pre-official Polymath work, I kept posting the current records online, with explanation of what the progress meant or how it happened.
I’m not an analyst or number theorist (I work in category theory), so I was content to read the progress of the project and learn how all this business worked. I’d read through Zhang’s preprint and was totally nonplussed, but the careful analysis—and exposition!—of Terry Tao and the other active participants made the ideas much clearer. In particular, concepts and tools that are well-known to analytic number theorists and are used without comment were brought into the open and discussed and explained.
When more specialised experts started working on subproblems, particularly numerical optimisation, it gave me snippets I could mention in my first-year algebra class to let them know how generalisations of the things they were learning (eigenvectors, symmetric matrices, convex optimisation etc) were being applied at the cutting edge of research. I even showed, on projector screens, Terry’s blog and the relevant comments, some made that very day. It has been a great opportunity to expose students of all stripes to the idea of research in pure mathematics, and that a problem in number theory needed serious tools from seemingly unrelated areas.
For me personally it felt like being able to sneak into the garage and watch a high-performance engine being built up from scratch; something I could never do, but could appreciate the end result, and admire the process.”
[Contribution added, thanks! – T.]
5 August, 2014 at 2:53 pm
Andrew Sutherland
Here are my comments for the retrospective.
“I first heard about Zhang’s result shortly after he spoke at Harvard in May, 2013. The techniques he used were well outside my main area of expertise, and I initially followed developments purely as a casual observer. It was only after reading Scott Morrison’s blog, where people had begun discussing improvements to Zhang’s bound, that I realized there was an interesting and essentially self-contained sub-problem (finding narrow admissible tuples) that looked amenable to number-theoretic combinatorial optimization algorithms, a subject with which I have some experience. I ran a few computations, and once I saw the results it was impossible to resist the urge to post them and join the polymath8 project. Aside from interest in the prime gaps problem, I was curious about the polymath phenomenon, and this seemed like a great opportunity to learn about it.
Like others, I was surprised by how much time I ended up devoting to the project. The initially furious pace of improvements and the public nature of the project made a very addictive combination, and I wound up spending most of that summer working on it. This meant delaying other work, but my collaborators on other projects were very supportive. I certainly do not begrudge the time I devoted to the polymath8 effort; it was a unique opportunity, and I’m glad I participated.
In terms of the polymath experience, there are a couple of things that stand out in my mind. In order to make the kind of rapid progress that can be achieved in a large scale collaboration, the participants really have to be comfortable with making mistakes in a forum that is both public and permanent. This can be a difficult adjustment, and there was certainly more than one occasion when I really wished I could retract something I had written that was obviously wrong. But one eventually gets used to working this way; the fact that everybody else is in the same boat helps. Actually, I think being forced to become more comfortable with making mistakes can be a very positive thing. This is how we learn.
The other thing that impressed me about the project is the wide range of people that made meaningful contributions. Not only were there plenty of participants who, like me, are not experts in analytic number theory, there were at least a few for whom mathematics is not their primary field of research. I think this is major strength of the polymath approach, it facilitates collaboration that would otherwise be very unlikely to occur.
It is perhaps worth highlighting some of the features of this project that made it a particularly good polymath candidate. First, the problem we were working on was well known and naturally attracted a lot of interested observers; this made it easy to recruit participants. Second, we had a clearly defined goal (improving the bound on prime gaps), and a metric against which incremental progress could be easily measured; this kept the project moving forward with lot of momentum. Third, the problem we were working on naturally split into sub-problems that were more or less independent; this allowed us to apply a lot of brain power in parallel, and when one branch of the project would slow down, another might speed up. Finally, we had an extremely capable project leader, one who could see the whole picture and was very adept at organizing and motivating people.
I don’t mean to suggest that these attributes are all necessary ingredients for a successful polymath project, but I think it is fair to say that, at least in this case, they were sufficient.”
5 August, 2014 at 3:02 pm
Pace Nielsen
“Finally, we had an extremely capable project leader, one who could see the whole picture and was very adept at organizing and motivating people.”
This is something I should have mentioned in my retrospective as well!
It is also somewhat surprising to me how many of us commented on the time we devoted to the project.
5 August, 2014 at 6:40 pm
Terence Tao
Thanks, Andrew, both for the retrospective contribution and for the nice words!
Now that we have a number of different contributions, I think maybe it is not so necessary to try to create a conclusions section, I think it actually works better when each contributor draws their own separate conclusions, although there does seem to be a remarkable amount of consensus amongst the participants. I’ll try to go over the retrospective article as a whole in the next day or two and do some polishing. Though I am debating as to whether to try to harmonise the writing styles (for instance, by making the capitalisation of “Polymath” uniform across contributions) – perhaps it actually would be more authentic to have each contributor write in their own personal style rather than try to enforce uniformity? (But I think we should certainly fix up typos and formatting errors, of course.)
8 August, 2014 at 7:31 pm
Terence Tao
I cleaned up the text (there was in particular an issue with apostrophes not being recognised by LaTeX that is nwo fixed) and decided to uniformise the capitalisation of “Polymath” as it was a bit jarring. We’re still waiting on a few more contributions, but I think it is beginning to take shape quite nicely.
18 August, 2014 at 2:45 pm
Andrew V. Sutherland
A couple of minor typos in the retrospective:
1. First sentence of section 5, “had be looking” should be “had been looking”.
2. There are still two uncapitalized occurrences of “polymath” in section 8 (first and fourth paras).
3. In the first para of section 9 you wrote “…Zhang had not published little in the area…” Perhaps you meant to write “had published little” (or “had not published much”)?
One general comment: I think the retrospective would read better if the contributions were listed more or less in the order they were posted to the blog, rather than being ordered alphabetically by last name. Many contributors refer to comments by others that were written chronologically earlier, but in most cases these appear later in the retrospective. In particular, I think it would make a lot of sense to put your comments (currently in section 9) first, this would really help to orient the reader.
[Corrections made, and sections now ordered chronologically – T.]
18 August, 2014 at 3:29 pm
Pace Nielsen
I agree with Andrew, and would propose the contributions be listed in chronological rather than alphabetical order.
14 August, 2014 at 1:31 am
Wouter Castryck
Here are some personal comments for the retrospective:
In June last year, one of my colleagues informed me about the polymath8 project and, in particular, about the programming challenge of finding admissible $k$-tuples whose diameter $H$ is as small as possible. I decided to give it a try and join “team $H$” of the production line. Luckily, I jumped in shortly after the project had started, at a point where there was still some low-hanging fruit. Like others I experienced how addictive it was to search for smaller values of $H$, while trying new computational tricks and combining them with ideas of the other participants. Because the value of $k$ kept decreasing as well, new challenges popped up every other day or so, which fueled the excitement. The whole event was intense and highly interactive, and progress was made at an incredible speed. (It is not academic to say so, but when the other teams managed to decrease $k$ to a size where our computational methods became superfluous, this was a bit of a disappointment. Luckily, Maynard’s work on prime triples, quadruples, … put larger values of $k$ back into play.)
Along the way it became clear that the online arena in which it all took place attracted many spectactors, and it felt like a privilege to be in there. It did require a mental switch to post naive (and sometimes wrong) ideas on the public forum, but in the end I agree with Andrew Sutherland that this is not necessarily a bad thing.
Gradually, by reading the blog posts, I also learned about the other parts of Zhang’s proof. On a personal level, this I found the most enriching bit: participating in the polymath8 project was a very stimulating way of learning and appreciating a new part of mathematics. This is definitely thanks to the clarifying and enthusing way in which Terence Tao administered the project. At the same time, I must admit that I did not grasp every detail from A to Z. From the point of view of a “coauthor” this is somewhat uncomfortable, but it may be inherent to the production line model along which the polymath projects are organized.
[Added to the retrospective, thanks – T.]
14 August, 2014 at 1:36 am
David Roberts
This is not too dissimilar to research projects in experimental fields, where people can contribute a part but not understand other parts. At the extreme end, the people in the teams at CERN may play some small part designing a bit of machinery, but not know about the latest data analysis techniques used to find a significant signal.
10 August, 2014 at 11:38 am
Eytan Paldi
A simple generalization of the weight function
is to replace the square in its definition (18) by any even power (e.g. a fourth power.)
This seems to emphasize the peaks of the weight function, but it is not clear how to generalize the needed asymptotics (in theorems 3.5, 3.6).
17 August, 2014 at 5:20 am
Eytan Paldi
In Polymath8b paper, in the last line of section 4.1 (page 20), it seems that in the
error contribution estimate, “
” can be replaced by “
“.
Therefore, it seems that condition (27) is not really needed !
17 August, 2014 at 7:58 am
Terence Tao
The way we are handling the summation over
here is to group the terms according to the value of the expression ![[d_1,d'_1] \dots [d_k,d'_k]](https://s0.wp.com/latex.php?latex=%5Bd_1%2Cd%27_1%5D+%5Cdots+%5Bd_k%2Cd%27_k%5D&bg=ffffff&fg=545454&s=0 "[d_1,d'_1] \dots [d_k,d'_k]")
. Each value of this expression indeed contributes 
to the error term; unfortunately, there are 
possible values of this expression, so the net size of this error is 
rather than 
.
17 August, 2014 at 8:25 am
Eytan Paldi
Thanks! (I now understand it.)
19 August, 2014 at 6:20 am
Eytan Paldi
In Polymath8b paper, page 19 line 6, “
” should be “
“.
[Corrected, thanks – T.]
20 August, 2014 at 4:26 pm
Eytan Paldi
In Polymath8b paper, the rightmost “
” in (31) should be “
“.
[Corrected, thanks -T.]
22 August, 2014 at 6:48 am
Eytan Paldi
In Polymath8b paper, the derivation in page 18 of the crude bounds for
can be simplified to
[Implemented, thanks – T.]
29 August, 2014 at 10:49 am
Eytan Paldi
In the explanation (the line below) of the first inequality, it is somewhat simpler to compare the magnitudes of the corresponding factors of the Euler products (instead of the corresponding terms of Dirichlet series.)
Similarly, the bound
for the expression above (38), can be replaced by
[Changes implemented, thanks – T.]
23 August, 2014 at 6:00 am
Gergely Harcos
Dear Terry, I can see you added the author affiliations to the retrospective paper, but mine are missing. I am a research advisor at Alfréd Rényi Institute of Mathematics and a professor at Central European University. Please add this information. Thank you!
[Oops, sorry about that! Added now – T.]
23 August, 2014 at 6:04 am
Eytan Paldi
In Polymath8b paper, page 18 line 5 from below, the maximum (defining the cubical integration domain) should be over the absolute values of the
variables.
[Corrected, thanks – T.]
24 August, 2014 at 10:17 am
Terence Tao
Emmanuel Kowalski has just added his contribution to the retrospective, and also brought my attention to this nice article (in French) by de la Breteche for the April 2014 issue of the Gazette of the Société Mathématique de France on prime gaps and on Polymath8.
25 August, 2014 at 3:11 pm
Pace Nielsen
According to Ken Ono’s facebook page, and also according to the polymath website: http://michaelnielsen.org/polymath1/index.php?title=Bounded_gaps_between_primes it appears that the paper has been accepted in RIMS.
Is that correct and/or official?
Either way, it is probably time for me to give the paper a final thorough read-through.
26 August, 2014 at 10:48 pm
Terence Tao
I suppose I should have posted that here: Ken sent me an email on Aug 2 saying that the paper had been accepted in principle, modulo the production people checking that the article format conformed to the standards of the journal, i.e. it is past the refereeing stage and onto the typesetting stage. I don’t think I’ve received any subsequent update yet.
28 August, 2014 at 11:43 am
Pace Nielsen
Thanks for the update. I’ve read through Section 4, and found the following minor changes to recommend. I would have made most of the changes myself, but I definitely don’t want to introduce a new error at this stage.
1. Page 6. In the statement of Theorem 2.3, the brackets around [5,62] are slanted. It might look nicer to put the brackets in roman type rather than italicized. (If we do this, do it again in Theorem 2.8)
2. Page 6. In Claim 2.6, the notation
is open to equivocation, as the comma could be interpretated as a break between two different mathematical quantities. (It’s okay as it stands, if we don’t want to make a change.)
Also, perhaps “pointwise bound” should be “pointwise bounds” since there are two of them? (OTOH they are both part of (6), so it is also okay as is.)
3. Page 7. In the proof of Proposition 2.7, the function
is introduced. This notation is defined earlier in the paper (in section 1.2) when it has a subscript. Perhaps this unsubscripted function should also be defined there.
4. Page 9. Table 1 is appearing in the middle of the statement of Theorem 3.3. It would be better to put it afterwards if possible.
5. Page 11. Two lines above (19), change “for various smooth functions” -> “for various fixed smooth compactly supported functions”. Also, both two lines earlier and one line later “linear combinations” are mentioned. Do we want to specify that they are “fixed” (even though this is obvious)?
6. Page 11. When deriving (21) from (14) and (20), there is the additional assumption that “
is supported on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0 "[0,1]")
“. How do we deduce this extra condition on the support? (If we don’t make that assumption on the support, but just assume 
, we have 
, which seems to work out, but I imagine there is something simple here I’m missing.)
7. Page 12. The normalization constant
, defined in the statement of Lemma 3.4 is used again here in Theorem 3.5 (and elsewhere in the paper). It should be clear to most readers what it’s definition is, but if we want to be exact perhaps after Lemma 3.4 we should say that 
continues to hold that same meaning everywhere else in the paper.
8. Page 14. In Theorem 3.13, instead of (xii’) it might look better to write (xii$’$), and make similar changes throughout the paper.
9. Page 22. Section 4.3, line 5 (the first off-set equation), the exponent has
, but I believe this should be 
. [This same typo also occurs in the in the last two offset equations of section 4.3, near the bottom of this same page.]
10. Page 23. In equations (48) and (49), the argument of the indicator function is (implicitly) only appearing in the subscript. It might be better to make the argument appear explicitly as an argument, and modify the subscript accordingly. E.g., in (48) perhaps writing something like
, and in (49) something like 
.
Alternatively, in Section 1, when defining indicator functions, we could explain how sometimes we will write the argument in the subscript. This alternative may be preferable as there are other places where this same notation is used.
11. Page 23. Last line– It seems that we can replace
with $\latex \leq$.
12. Page 24. In the offset equation above (50), should
be 
?
13. Page 25. Line 2 (first offset equation). The superscript on
is missing a right-most parenthesis.
14. Page 27. Last line (above the footnote). I believe we want to change “divides
and 
” -> “divides 
and 
”
—
I also did a quick spell-check and double-word check.
Page 73. Misspelled word: “adjustements”
Page 75. Double words: “by examining the the entries”, “If we sieve the the residue class”, and “This will typically happen for for some”
—
Things I’m still struggling to understand within the first four sections.
Page 30. How is Proposition 4.2 being applied? I’m just not immediately seeing the connection. (It may be obvious, I am still a little jet-lagged.)
[Corrected, thanks, with the argument invoking Proposition 4.2 in page 30 reworded. -T.]
28 August, 2014 at 11:47 am
Pace Nielsen
In item (2) above, the two
symbols should be curly 
symbols.
25 August, 2014 at 7:40 pm
arch1
Beginner Q: Section 2 (p.5) introduces distributional estimates on the von Mangoldt function, which “serves as a proxy for the primes.” Does this mean that as x gets large, prime powers beyond the 1st contribute negligibly to the LHS of Claim 2.2?
[That is certainly one of the key features of the von Mangoldt function that make it a good proxy for the primes, yes. -T.]
28 August, 2014 at 10:30 am
arch1
p. 4, near the middle of Section 1.1, “…in combination of Lemma 3.4…”: of -> with
[Corrected (for the Polymath8b paper), thanks -T.]
28 August, 2014 at 2:24 pm
Pace Nielsen
Thanks Terry for making the changes I suggested above!
One final question. What happens to the arguments when we replace (20) by the condition
(which is what happens by dropping the assumption that 
is supported on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0 "[0,1]")
, but still assume 
is a prime in the range ![[x,2x]](https://s0.wp.com/latex.php?latex=%5Bx%2C2x%5D&bg=ffffff&fg=545454&s=0 "[x,2x]")
)? I quickly ran through the arguments, so I may have missed something, but it seems to me that:
1. The
term can be safely ignored.
2. Instead of
in a couple formulas, we just replace that factor with 
, and similar looking (but slightly more complicated) integral formulas arise for the asymptotic constants.
Is this a cheap way to get around the support restriction, or is there some obstruction I’ve missed?
28 August, 2014 at 3:46 pm
Terence Tao
Yes, I think one would still get asymptotics in this case. I think though in our situation we never deal with supports that get as far as 1; I think the largest support we have to deal with is [0,3/4]. (The “classical” simplex
only gets as far as 1/2, and we do play with an enlarged simplex 
, but even in the case when 
and 
, this only reaches as far as 3/4.)
29 August, 2014 at 7:34 am
arch1
Polymath 8b paper, Page 57.7: “with be” -> “will be”
Page 58.6: “We took d = 23 and imposing” -> “We took d = 23 and imposed”
Page 61.4: “If we use … and sets … one can compute” -> “If one uses … and sets … one can compute”
Page 61.6: “supported the simplex” -> “supported in(?) the simplex”
Page 62, formula (133): is it (x,y), rather than z, which should be in polygon Qi?
Page 62.6: “on the coefficients on the Fi” -> “on the coefficients of the Fi”?
Page 62, last two lines: you might want to be consistent about “x + y” vs. “y + x”
Page 64, last line: what are “these regions”? (sorry if this is obvious; just skimming)
Page 67.0: should the 2nd integral after “signed definite integral” have its limits interchanged?
[Corrected, thanks – T.]
29 August, 2014 at 7:45 am
arch1
please ignore the Page 67.0 item, I must have vertical dyslexia
29 August, 2014 at 10:10 am
arch1
Polymath 8b paper, Pages 47-55: naïve scan didn’t catch anything
Page 56.4: “finite set b1,…” -> “finite set of functions b1,…”?
[Corrected, thanks – T.]
29 August, 2014 at 12:57 pm
arch1
Polymath 8b paper, Page 8: “…smaller than k, in fact j…” -> “…smaller than k; in fact, j…”
Page 68: In the first summation subscript of (142) and (144), is it really x (and not say n+h, or n) that should =a(q)?
Page 68: Are the parenthetical remarks preceding and following (143) both needed?
Page 78.2: “is already admissibility” -> “is already admissible”
Page 78.6: “msuch” -> “m such”
It might help if someone else who doesn’t know too much math would “naïve-scan” the 8b paper. Having done a casual such scan of pages 42-78 (and assuming pages 1-10 have gotten a lot of scrutiny), I guess pages 11-41 would benefit most.
[Corrected, thanks – T.]
30 August, 2014 at 10:41 am
Eytan Paldi
In Polymath8b paper (page 30), it seems that in (65)-(67) the difference operators
“
” should be
“
”
[Corrected, thanks – T.]
31 August, 2014 at 12:23 am
Eytan Paldi
It should still be corrected at four places (one in (65), two in (66) and one in (67)).
[Corrected, thanks – T.]
30 August, 2014 at 6:16 pm
Terence Tao
I forgot to mention this earlier, but about five days ago, Emmanuel and Phillipe finished their streamlining of the Polymath8a paper. I’ve now gone through it also, and am pretty happy with it (and it has addressed all the referee concerns). I’ll wait for another week to see if there are more changes to be made, but then we can send it back to Andrew Granville at A&NT. The retrospective is almost complete too, so it looks like all three papers coming out of Polymath8 are on track.
31 August, 2014 at 1:23 am
Wouter Castryck
Some minor comments:
On page 1, “there exists even integers” –> “there exist”.
On page 3, I didn’t understand the sentence concerning the polynomial
: is this a single polynomial (in which case it may be better to write 
in the subscript?).
On page 6, “In addition …, there are some additional concepts …”. Maybe we can just write “There are some additional concepts …”?
On page 8, there is a
that should be 
.
On page 12 in step (0) of the proof: “in checking that an integer
is 
-d.d., it suffices …” –> “in checking that an integer 
is 
-d.d, it suffices …” (removed dot)
On page 61 there are two occurrences of
that should be 
for consistency (or the other way round, but then there are more changes to make).
On page 74 in Remark 6.18 in the definition of
there is a 
that should be a 
.
Reference [11]: “probléme” –> “problème”
[Corrected, thanks – though I believe the second dot in d.d. will still be needed to signify the abbreviation. -T.]
3 September, 2014 at 11:31 am
Terence Tao
I’ve now sent the revised version of Polymath8a back to Algebra & Number Theory.
1 September, 2014 at 1:28 pm
Eytan Paldi
In the retrospective paper, Turan and Erdos names (References [13] and [32]) are misspelled.
[Corrected, thanks – T.]
1 September, 2014 at 8:16 pm
arch1
Polymath 8b paper:
Page 13.3: “establishing certain variational problems” -> “establishing certain variational results” ?
Page 13.7: “square integrable” -> “square-integrable”
Page 14.4: “be the defined” -> “be defined”
Page 14.4: “square-integrable F supported in” -> “square-integrable functions F that are supported in”
Page 15.3: “square integrable functions” -> “square-integrable functions”
Page 15.5: “one of the following..hold” -> “one of the following..holds”
Page 15.9, “there is also a version corresponding to part (i) also”: strike an “also”
Page 19.9: “…replace [dj , d’j] with…]” -> “…replace the denominators [dj , d’j] with…]”
[Corrected, thanks – T.]
2 September, 2014 at 2:08 am
Eytan Paldi
In Polymathe8b paper, after the definition of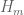
in the abstract, it seems clearer to add (as in the introduction) the definition of 
.
Also, in the first line of page 46, “[52]” should be “[53]”.
[Corrected, thanks – T.]
2 September, 2014 at 10:19 am
Terence Tao
Thanks to all for the many corrections on the Polymath8b paper! The RIMS production staff at Springer are now asking for the LaTeX source, so I’ll wait until this evening for any last remaining corrections and then submit the source to them (and also update the arXiv copy).
2 September, 2014 at 6:37 pm
Terence Tao
OK, I have sent back the source files and updated the arXiv copy.
3 September, 2014 at 1:49 pm
Eytan Paldi
In the main page of Polymath8, the links for the arXiv copies of Polymath8a and Polymath8b papers are still for older versions.
[It may take about 24 hours or so for the arXiv to update. -T.]
2 September, 2014 at 3:17 pm
arch1
Polymath 8b paper:
Page 21.5: Is the meaning of “this contribution” sufficiently clear?
Page 25.3: In the inequality following “We see that”, and in the RHS expansion 2 lines further on, are the ‘3-bar-equals’ signs intended?
Page 29.0: “In particular, the…tuples..contributes…” -> “In particular, the…tuples…contribute…”
Page 30.2: In the LHS of the 2nd standalone equation, shouldn’t all inequalities between the pi (& thus the 5th inequality symbol) be strict?
Page 32.6, “Now that we have proven…we can now establish…”: strike the 2nd “now”
Page 34.8: “..convolves…by…” -> “…convolves…with…” ?
Page 36.2, 2nd equation: Is it allowed to have a top-heavy partial derivative like that?
Page 38.0: “…holds, then…” -> “…holds; then…” (ditto in the next sentence)
Page 38.4: “for some i0 = 1,…,k” -> “for some 1 lte i0 lte k”??
Page 38.6: “…this and Theorem 3.5 is not strong enough…” -> “…this combined with Theorem 3.5 is not strong enough…”?
Page 41.2 “supported of intervals” -> “supported on intervals”
Page 41.2 “with the support of each component…supported in” -> “with each component…supported in”
(end of casual “naive scan”)
[Corrected, thanks – T.]
5 September, 2014 at 2:26 pm
Anonymous
Polymath 8b paper, v3 on http://arxiv.org/pdf/1407.4897v3.pdf.
The following are for the bibliography:
– Ref. 7: $156$ –> $\mathbf{156}$
– Ref. 10: $70$ –> $\mathbf{70}$
– Ref. 11: $52$ –> $\mathbf{52}$
– Ref. 12: $33$ –> $\mathbf{33}$
– Ref. 13: $4$ –> $\mathbf{4}$
– Ref. 14: to appear in: –> to appear in
– Ref. 16: $152$ –> $\mathbf{152}$ + E. –> É [two things]
– Ref. 20: $4$ –> $\mathbf{4}$
– Ref. 21: 945—1040 –> 945–1040
– Ref. 22: $42$ –> $\mathbf{42}$
– Ref. 25: $170$ –> $\mathbf{170}$
– Ref. 26: $361$ –> $\mathbf{361}$
– Ref. 30: $44$ –> $\mathbf{44}$
– Ref. 31: $34$ –> $\mathbf{34}$
– Ref. 32: pp. 123–127 –> 123–127
– Ref. 33: $25$ –> $\mathbf{25}$
– Ref. 34: Publications Vol. $53$ –> Publications, vol. $53$ [two things]
– Ref. 36: $34$ –> $\mathbf{34}$
– Ref. 40: volume $227$ of Lecture Notes in Math. Springer –> Lecture Notes in Math. Springer, vol. 227 [two things]
– Ref. 42: $52$ –> $\mathbf{52}$
– Ref. 43: $40$ –> $\mathbf{40}$
– Ref. 44: pp. 525–559 –> 525–559
– Ref. 54: $80$ –> $\mathbf{80}$
– Ref. 55: $7$ (1961/1962) 1–8 –> $\mathbf{7}$ (1961/1962), 1–8 [two things]
– Ref. 56: $7$ –> $\mathbf{7}$
– Ref. 57: Vol. I –> vol. I
– Ref. 58: in: –> in
– Ref. 59: $44$ –> $\mathbf{44}$
– Ref. 22 should in between ref. 17 and 18
7 September, 2014 at 2:55 am
Eytan Paldi
In Polymath8 home page, the table of current records (“without EH”) should be updated to the bounds in Polymath8b paper (theorem 1.4(ii)-(vi)).
[Actually, the records are slightly better than the 8b paper, because they use a provisional equidistribution estimate whose proof has not been fully written up due to the need to check some tricky algebraic geometry. There are some people looking to flesh out the details of that estimate, though this would be done by a more traditional collaboration, i.e. outside of the Polymath8 project scope. -T.]
18 September, 2014 at 10:50 am
Eytan Paldi
In Polymath8b paper (page 18), the factorization of the integral kernel
into the factors 
(given by (39)) may be verified via the following very general (and simple!) factorization principle:
Let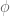
be a bijection from the product of finite nonempty sets 
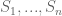onto a set 
. Let 
be a complex-valued function on 
with the (factorization) property:
For every
, where 
are certain complex-valued functions on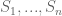 
, correspondingly. Therefore
Remark: This factorization principle is for finite sums and products (but under certain regularity conditions it may be extended for countable sums and products.)
25 September, 2014 at 1:48 pm
Terence Tao
Just a note that all of the people who had agreed to contribute to the retrospective article at https://www.dropbox.com/sh/koxbhwvw1ysybk9/AADTJ4w3yegvgTut_Tsv0Sana/retrospective.pdf have now done so. I’ll wait until Monday in case there are any last minute edits or suggestions, and then submit to the EMS newsletter.
26 September, 2014 at 12:56 pm
Eytan Paldi
In the definition of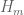
(in both the abstract and introduction), 
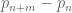should be inside parentheses.
[Corrected, thanks – T.]
28 September, 2014 at 1:13 am
Eytan Paldi
It should also be corrected in the introduction (page2, line 14 from below.)
[Corrected, thanks – T.]
28 September, 2014 at 7:40 am
Eytan Paldi
The closing parenthesis is misplaced.
[Corrected, thanks – T.]
29 September, 2014 at 4:40 am
Eytan Paldi
In the retrospective article, after “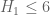
” in the introduction (line10 above the introduction end), “generalized” should be added before “Elliott-Halberstam conjecture”.
[Corrected, thanks – T.]
25 September, 2014 at 3:03 pm
Anonymous
Footnote 5: “Nelson and” –> “Nelson, and”
Footnote 6: “the” –> “The” + “2004” –> “2004.”
[Corrected, thanks – T.]
27 September, 2014 at 5:36 am
Eytan Paldi
Some typos:
1. In Polymath8a paper (definition 1.4 in the old unabridged version, definition 1.2 in the new version) and in Polymath8b paper (definition 1.6), it seems that “
” should be “
“.
” should be “
” in line 4, and “
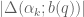” in line 6.
2. In Polymath8a paper (page 22), “
[Corrected, thanks – T.]
27 September, 2014 at 7:14 am
Anonymous
Retrospective article, Terrence Tao’s input:
– P. 3, l. -4: “The first that” –> “The first time that”?
– P. 3, l. -1: “skeptical – the” –> “skeptical—the” or “skeptical\,—\,the”
– P. 7, 2nd paragraph, l. 7: “size – 163” –> “size—163” or “size\,—\,163”
[Corrected, thanks – T.]
29 September, 2014 at 5:59 pm
Terence Tao
I’ve submitted the retrospective to the newsletter of the EMS and uploaded it to the arXiv. I’ll make a blog post about it when the arXiv paper comes out (and it’s about time to roll over the polymath8 thread again anyway, though presumably this will be the final time to do so, as the project now seems to be more or less concluded).
30 September, 2014 at 12:20 pm
Eytan Paldi
In polymath8b paper, in the line below the estimate (2), “[52, Lemma 1.5]” should be “[53, Lemma 1.5]” (or “[52, Lemma 1.3]”), but it seems that (2) is not explicitly stated in these lemmas.
[Corrected, thanks – T.]
1 October, 2014 at 2:22 am
Eytan Paldi
In Polymath8b paper (page 5), “[52, Lemma 1.5]” (in the line below the estimate (2)) should still be corrected to “[52, Lemma 1.3]” – since lemma 1.5 of the older unabridge version [53] is now lemma 1.3 of the new version [52] of Polymath8a paper.
Although the estimate (2) is not explicitly stated in [52, lemma 1.3], it easily follows (using summation by parts) from [52, lemma 1.3(ii)].
[Oops, the correction did not update properly before; fixed now. -T.]
30 September, 2014 at 8:58 pm
The “bounded gaps between primes” Polymath project – a retrospective | What's new
[…] post will also serve as the latest (and probably last) of the Polymath8 threads (rolling over this previous post), to wrap up any remaining discussion about any aspect of this […]
6 October, 2014 at 5:09 pm
Anon
The “work of Zhang” anchor is broken.
[Corrected, thanks – T.]
19 March, 2016 at 9:11 am
Ila
I do believe all the ideas you have introducerd for our post.
They’rereally convincing and can definitely work.
Nonetheless, the posts are very brief for novices. May just you please extend
them a litttle from neext time? Thanks for the post.
17 July, 2016 at 8:54 am
Notes on the Bombieri asymptotic sieve | What's new
[…] of the generalised Elliott-Halberstam (GEH) conjecture (as formulated for instance in Claim 2.6 of the Polymath8b paper), one can also swap the factor in the above asymptotics with other parity-violating weights and […]