Real analysis relative to a finite measure space

15 July, 2014 in expository, math.CA, math.CT, math.PR, math.SP | Tags: elementary topos, Heine-Borel theorem, Hilbert modules, Hilbert-Schmidt operators, singular value decomposition, spectral theorem | by Terence Tao

In the traditional foundations of probability theory, one selects a probability space ${(\Omega, {\mathcal B}, {\mathbf P})}$ , and makes a distinction between deterministic mathematical objects, which do not depend on the sampled state ${\omega \in \Omega}$ , and stochastic (or random) mathematical objects, which do depend (but in a measurable fashion) on the sampled state ${\omega \in \Omega}$ . For instance, a deterministic real number would just be an element ${x \in {\bf R}}$ , whereas a stochastic real number (or real random variable) would be a measurable function ${x: \Omega \rightarrow {\bf R}}$ , where in this post ${{\bf R}}$ will always be endowed with the Borel ${\sigma}$ -algebra. (For readers familiar with nonstandard analysis, the adjectives “deterministic” and “stochastic” will be used here in a manner analogous to the uses of the adjectives “standard” and “nonstandard” in nonstandard analysis. The analogy is particularly close when comparing with the “cheap nonstandard analysis” discussed in this previous blog post. We will also use “relative to ${\Omega}$ ” as a synonym for “stochastic”.)

Actually, for our purposes we will adopt the philosophy of identifying stochastic objects that agree almost surely, so if one was to be completely precise, we should define a stochastic real number to be an equivalence class ${[x]}$ of measurable functions ${x: \Omega \rightarrow {\bf R}}$ , up to almost sure equivalence. However, we shall often abuse notation and write ${[x]}$ simply as ${x}$ .

More generally, given any measurable space ${X = (X, {\mathcal X})}$ , we can talk either about deterministic elements ${x \in X}$ , or about stochastic elements of ${X}$ , that is to say equivalence classes ${[x]}$ of measurable maps ${x: \Omega \rightarrow X}$ up to almost sure equivalence. We will use ${\Gamma(X|\Omega)}$ to denote the set of all stochastic elements of ${X}$ . (For readers familiar with sheaves, it may helpful for the purposes of this post to think of ${\Gamma(X|\Omega)}$ as the space of measurable global sections of the trivial ${X}$ –bundle over ${\Omega}$ .) Of course every deterministic element ${x}$ of ${X}$ can also be viewed as a stochastic element ${x|\Omega \in \Gamma(X|\Omega)}$ given by (the equivalence class of) the constant function ${\omega \mapsto x}$ , thus giving an embedding of ${X}$ into ${\Gamma(X|\Omega)}$ . We do not attempt here to give an interpretation of ${\Gamma(X|\Omega)}$ for sets ${X}$ that are not equipped with a ${\sigma}$ -algebra ${{\mathcal X}}$ .

Remark 1 In my previous post on the foundations of probability theory, I emphasised the freedom to extend the sample space ${(\Omega, {\mathcal B}, {\mathbf P})}$ to a larger sample space whenever one wished to inject additional sources of randomness. This is of course an important freedom to possess (and in the current formalism, is the analogue of the important operation of base change in algebraic geometry), but in this post we will focus on a single fixed sample space ${(\Omega, {\mathcal B}, {\mathbf P})}$ , and not consider extensions of this space, so that one only has to consider two types of mathematical objects (deterministic and stochastic), as opposed to having many more such types, one for each potential choice of sample space (with the deterministic objects corresponding to the case when the sample space collapses to a point).

Any (measurable) ${k}$ -ary operation on deterministic mathematical objects then extends to their stochastic counterparts by applying the operation pointwise. For instance, the addition operation ${+: {\bf R} \times {\bf R} \rightarrow {\bf R}}$ on deterministic real numbers extends to an addition operation ${+: \Gamma({\bf R}|\Omega) \times \Gamma({\bf R}|\Omega) \rightarrow \Gamma({\bf R}|\Omega)}$ , by defining the class ${[x]+[y]}$ for ${x,y: \Omega \rightarrow {\bf R}}$ to be the equivalence class of the function ${\omega \mapsto x(\omega) + y(\omega)}$ ; this operation is easily seen to be well-defined. More generally, any measurable ${k}$ -ary deterministic operation ${O: X_1 \times \dots \times X_k \rightarrow Y}$ between measurable spaces ${X_1,\dots,X_k,Y}$ extends to an stochastic operation ${O: \Gamma(X_1|\Omega) \times \dots \Gamma(X_k|\Omega) \rightarrow \Gamma(Y|\Omega)}$ in the obvious manner.

There is a similar story for ${k}$ -ary relations ${R: X_1 \times \dots \times X_k \rightarrow \{\hbox{true},\hbox{false}\}}$ , although here one has to make a distinction between a deterministic reading of the relation and a stochastic one. Namely, if we are given stochastic objects ${x_i \in \Gamma(X_i|\Omega)}$ for ${i=1,\dots,k}$ , the relation ${R(x_1,\dots,x_k)}$ does not necessarily take values in the deterministic Boolean algebra ${\{ \hbox{true}, \hbox{false}\}}$ , but only in the stochastic Boolean algebra ${\Gamma(\{ \hbox{true}, \hbox{false}\}|\Omega)}$ – thus ${R(x_1,\dots,x_k)}$ may be true with some positive probability and also false with some positive probability (with the event that ${R(x_1,\dots,x_k)}$ being stochastically true being determined up to null events). Of course, the deterministic Boolean algebra embeds in the stochastic one, so we can talk about a relation ${R(x_1,\dots,x_k)}$ being determinstically true or deterministically false, which (due to our identification of stochastic objects that agree almost surely) means that ${R(x_1(\omega),\dots,x_k(\omega))}$ is almost surely true or almost surely false respectively. For instance given two stochastic objects ${x,y}$ , one can view their equality relation ${x=y}$ as having a stochastic truth value. This is distinct from the way the equality symbol ${=}$ is used in mathematical logic, which we will now call “equality in the deterministic sense” to reduce confusion. Thus, ${x=y}$ in the deterministic sense if and only if the stochastic truth value of ${x=y}$ is equal to ${\hbox{true}}$ , that is to say that ${x(\omega)=y(\omega)}$ for almost all ${\omega}$ .

Any universal identity for deterministic operations (or universal implication between identities) extends to their stochastic counterparts: for instance, addition is commutative, associative, and cancellative on the space of deterministic reals ${{\bf R}}$ , and is therefore commutative, associative, and cancellative on stochastic reals ${\Gamma({\bf R}|\Omega)}$ as well. However, one has to be more careful when working with mathematical laws that are not expressible as universal identities, or implications between identities. For instance, ${{\bf R}}$ is an integral domain: if ${x_1,x_2 \in {\bf R}}$ are deterministic reals such that ${x_1 x_2=0}$ , then one must have ${x_1=0}$ or ${x_2=0}$ . However, if ${x_1, x_2 \in \Gamma({\bf R}|\Omega)}$ are stochastic reals such that ${x_1 x_2 = 0}$ (in the deterministic sense), then it is no longer necessarily the case that ${x_1=0}$ (in the deterministic sense) or that ${x_2=0}$ (in the deterministic sense); however, it is still true that “ ${x_1=0}$ or ${x_2=0}$ ” is true in the deterministic sense if one interprets the boolean operator “or” stochastically, thus “ ${x_1(\omega)=0}$ or ${x_2(\omega)=0}$ ” is true for almost all ${\omega}$ . Another way to properly obtain a stochastic interpretation of the integral domain property of ${{\bf R}}$ is to rewrite it as

$\displaystyle x_1,x_2 \in {\bf R}, x_1 x_2 = 0 \implies x_i=0 \hbox{ for some } i \in \{1,2\}$

and then make all sets stochastic to obtain the true statement

$\displaystyle x_1,x_2 \in \Gamma({\bf R}|\Omega), x_1 x_2 = 0 \implies x_i=0 \hbox{ for some } i \in \Gamma(\{1,2\}|\Omega),$

thus we have to allow the index ${i}$ for which vanishing ${x_i=0}$ occurs to also be stochastic, rather than deterministic. (A technical note: when one proves this statement, one has to select ${i}$ in a measurable fashion; for instance, one can choose ${i(\omega)}$ to equal ${1}$ when ${x_1(\omega)=0}$ , and ${2}$ otherwise (so that in the “tie-breaking” case when ${x_1(\omega)}$ and ${x_2(\omega)}$ both vanish, one always selects ${i(\omega)}$ to equal ${1}$ ).)

Similarly, the law of the excluded middle fails when interpreted deterministically, but remains true when interpreted stochastically: if ${S}$ is a stochastic statement, then it is not necessarily the case that ${S}$ is either deterministically true or deterministically false; however the sentence “ ${S}$ or not- ${S}$ ” is still deterministically true if the boolean operator “or” is interpreted stochastically rather than deterministically.

To avoid having to keep pointing out which operations are interpreted stochastically and which ones are interpreted deterministically, we will use the following convention: if we assert that a mathematical sentence ${S}$ involving stochastic objects is true, then (unless otherwise specified) we mean that ${S}$ is deterministically true, assuming that all relations used inside ${S}$ are interpreted stochastically. For instance, if ${x,y}$ are stochastic reals, when we assert that “Exactly one of ${x < y}$ , ${x=y}$ , or ${x>y}$ is true”, then by default it is understood that the relations ${<}$ , ${=}$ , ${>}$ and the boolean operator “exactly one of” are interpreted stochastically, and the assertion is that the sentence is deterministically true.

In the above discussion, the stochastic objects ${x}$ being considered were elements of a deterministic space ${X}$ , such as the reals ${{\bf R}}$ . However, it can often be convenient to generalise this situation by allowing the ambient space ${X}$ to also be stochastic. For instance, one might wish to consider a stochastic vector ${v(\omega)}$ inside a stochastic vector space ${V(\omega)}$ , or a stochastic edge ${e}$ of a stochastic graph ${G(\omega)}$ . In order to formally describe this situation within the classical framework of measure theory, one needs to place all the ambient spaces ${X(\omega)}$ inside a measurable space. This can certainly be done in many contexts (e.g. when considering random graphs on a deterministic set of vertices, or if one is willing to work up to equivalence and place the ambient spaces inside a suitable moduli space), but is not completely natural in other contexts. For instance, if one wishes to consider stochastic vector spaces of potentially unbounded dimension (in particular, potentially larger than any given cardinal that one might specify in advance), then the class of all possible vector spaces is so large that it becomes a proper class rather than a set (even if one works up to equivalence), making it problematic to give this class the structure of a measurable space; furthermore, even once one does so, one needs to take additional care to pin down what it would mean for a random vector ${\omega \mapsto v_\omega}$ lying in a random vector space ${\omega \mapsto V_\omega}$ to depend “measurably” on ${\omega}$ .

Of course, in any reasonable application one can avoid the set theoretic issues at least by various ad hoc means, for instance by restricting the dimension of all spaces involved to some fixed cardinal such as ${2^{\aleph_0}}$ . However, the measure-theoretic issues can require some additional effort to resolve properly.

In this post I would like to describe a different way to formalise stochastic spaces, and stochastic elements of these spaces, by viewing the spaces as measure-theoretic analogue of a sheaf, but being over the probability space ${\Omega}$ rather than over a topological space; stochastic objects are then sections of such sheaves. Actually, for minor technical reasons it is convenient to work in the slightly more general setting in which the base space ${\Omega}$ is a finite measure space ${(\Omega, {\mathcal B}, \mu)}$ rather than a probability space, thus ${\mu(\Omega)}$ can take any value in ${[0,+\infty)}$ rather than being normalised to equal ${1}$ . This will allow us to easily localise to subevents ${\Omega'}$ of ${\Omega}$ without the need for normalisation, even when ${\Omega'}$ is a null event (though we caution that the map ${x \mapsto x|\Omega'}$ from deterministic objects ${x}$ ceases to be injective in this latter case). We will however still continue to use probabilistic terminology. despite the lack of normalisation; thus for instance, sets ${E}$ in ${{\mathcal B}}$ will be referred to as events, the measure ${\mu(E)}$ of such a set will be referred to as the probability (which is now permitted to exceed ${1}$ in some cases), and an event whose complement is a null event shall be said to hold almost surely. It is in fact likely that almost all of the theory below extends to base spaces which are ${\sigma}$ -finite rather than finite (for instance, by damping the measure to become finite, without introducing any further null events), although we will not pursue this further generalisation here.

The approach taken in this post is “topos-theoretic” in nature (although we will not use the language of topoi explicitly here), and is well suited to a “pointless” or “point-free” approach to probability theory, in which the role of the stochastic state ${\omega \in \Omega}$ is suppressed as much as possible; instead, one strives to always adopt a “relative point of view”, with all objects under consideration being viewed as stochastic objects relative to the underlying base space ${\Omega}$ . In this perspective, the stochastic version of a set is as follows.

Definition 1 (Stochastic set) Unless otherwise specified, we assume that we are given a fixed finite measure space ${\Omega = (\Omega, {\mathcal B}, \mu)}$ (which we refer to as the base space). A stochastic set (relative to ${\Omega}$ ) is a tuple ${X|\Omega = (\Gamma(X|E)_{E \in {\mathcal B}}, ((|E))_{E \subset F, E,F \in {\mathcal B}})}$ consisting of the following objects:

A set ${\Gamma(X|E)}$ assigned to each event ${E \in {\mathcal B}}$ ; and

A restriction map ${x \mapsto x|E}$ from ${\Gamma(X|F)}$ to ${\Gamma(X|E)}$ to each pair ${E \subset F}$ of nested events ${E,F \in {\mathcal B}}$ . (Strictly speaking, one should indicate the dependence on ${F}$ in the notation for the restriction map, e.g. using ${x \mapsto x|(E \leftarrow F)}$ instead of ${x \mapsto x|E}$ , but we will abuse notation by omitting the ${F}$ dependence.)

We refer to elements of ${\Gamma(X|E)}$ as local stochastic elements of the stochastic set ${X|\Omega}$ , localised to the event ${E}$ , and elements of ${\Gamma(X|\Omega)}$ as global stochastic elements (or simply elements) of the stochastic set. (In the language of sheaves, one would use “sections” instead of “elements” here, but I prefer to use the latter terminology here, for compatibility with conventional probabilistic notation, where for instance measurable maps from ${\Omega}$ to ${{\bf R}}$ are referred to as real random variables, rather than sections of the reals.)

Furthermore, we impose the following axioms:

(Category) The map ${x \mapsto x|E}$ from ${\Gamma(X|E)}$ to ${\Gamma(X|E)}$ is the identity map, and if ${E \subset F \subset G}$ are events in ${{\mathcal B}}$ , then ${((x|F)|E) = (x|E)}$ for all ${x \in \Gamma(X|G)}$ .

(Null events trivial) If ${E \in {\mathcal B}}$ is a null event, then the set ${\Gamma(X|E)}$ is a singleton set. (In particular, ${\Gamma(X|\emptyset)}$ is always a singleton set; this is analogous to the convention that ${x^0=1}$ for any number ${x}$ .)

(Countable gluing) Suppose that for each natural number ${n}$ , one has an event ${E_n \in {\mathcal B}}$ and an element ${x_n \in \Gamma(X|E_n)}$ such that ${x_n|(E_n \cap E_m) = x_m|(E_n \cap E_m)}$ for all ${n,m}$ . Then there exists a unique ${x\in \Gamma(X|\bigcup_{n=1}^\infty E_n)}$ such that ${x_n = x|E_n}$ for all ${n}$ .

If ${\Omega'}$ is an event in ${\Omega}$ , we define the localisation ${X|\Omega'}$ of the stochastic set ${X|\Omega}$ to ${\Omega'}$ to be the stochastic set

$\displaystyle X|\Omega' := (\Gamma(X|E)_{E \in {\mathcal B}; E \subset \Omega'}, ((|E))_{E \subset F \subset \Omega', E,F \in {\mathcal B}})$

relative to ${\Omega'}$ . (Note that there is no need to renormalise the measure on ${\Omega'}$ , as we are not demanding that our base space have total measure ${1}$ .)

The following fact is useful for actually verifying that a given object indeed has the structure of a stochastic set:

Exercise 1 Show that to verify the countable gluing axiom of a stochastic set, it suffices to do so under the additional hypothesis that the events ${E_n}$ are disjoint. (Note that this is quite different from the situation with sheaves over a topological space, in which the analogous gluing axiom is often trivial in the disjoint case but has non-trivial content in the overlapping case. This is ultimately because a ${\sigma}$ -algebra is closed under all Boolean operations, whereas a topology is only closed under union and intersection.)

Let us illustrate the concept of a stochastic set with some examples.

Example 1 (Discrete case) A simple case arises when ${\Omega}$ is a discrete space which is at most countable. If we assign a set ${X_\omega}$ to each ${\omega \in \Omega}$ , with ${X_\omega}$ a singleton if ${\mu(\{\omega\})=0}$ . One then sets ${\Gamma(X|E) := \prod_{\omega \in E} X_\omega}$ , with the obvious restriction maps, giving rise to a stochastic set ${X|\Omega}$ . (Thus, a local element ${x}$ of ${\Gamma(X|E)}$ can be viewed as a map ${\omega \mapsto x(\omega)}$ on ${E}$ that takes values in ${X_\omega}$ for each ${\omega \in E}$ .) Conversely, it is not difficult to see that any stochastic set over an at most countable discrete probability space ${\Omega}$ is of this form up to isomorphism. In this case, one can think of ${X|\Omega}$ as a bundle of sets ${X_\omega}$ over each point ${\omega}$ (of positive probability) in the base space ${\Omega}$ . One can extend this bundle interpretation of stochastic sets to reasonably nice sample spaces ${\Omega}$ (such as standard Borel spaces) and similarly reasonable ${X}$ ; however, I would like to avoid this interpretation in the formalism below in order to be able to easily work in settings in which ${\Omega}$ and ${X}$ are very “large” (e.g. not separable in any reasonable sense). Note that we permit some of the ${X_\omega}$ to be empty, thus it can be possible for ${\Gamma(X|\Omega)}$ to be empty whilst ${\Gamma(X|E)}$ for some strict subevents ${E}$ of ${\Omega}$ to be non-empty. (This is analogous to how it is possible for a sheaf to have local sections but no global sections.) As such, the space ${\Gamma(X|\Omega)}$ of global elements does not completely determine the stochastic set ${X|\Omega}$ ; one sometimes needs to localise to an event ${E}$ in order to see the full structure of such a set. Thus it is important to distinguish between a stochastic set ${X|\Omega}$ and its space ${\Gamma(X|\Omega)}$ of global elements. (As such, it is a slight abuse of the axiom of extensionality to refer to global elements of ${X|\Omega}$ simply as “elements”, but hopefully this should not cause too much confusion.)

Example 2 (Measurable spaces as stochastic sets) Returning now to a general base space ${\Omega}$ , any (deterministic) measurable space ${X}$ gives rise to a stochastic set ${X|\Omega}$ , with ${\Gamma(X|E)}$ being defined as in previous discussion as the measurable functions from ${E}$ to ${X}$ modulo almost everywhere equivalence (in particular, ${\Gamma(X|E)}$ a singleton set when ${E}$ is null), with the usual restriction maps. The constraint of measurability on the maps ${x: E \rightarrow \Omega}$ , together with the quotienting by almost sure equivalence, means that ${\Gamma(X|E)}$ is now more complicated than a plain Cartesian product ${\prod_{\omega \in E} X_\omega}$ of fibres, but this still serves as a useful first approximation to what ${\Gamma(X|E)}$ is for the purposes of developing intuition. Indeed, the measurability constraint is so weak (as compared for instance to topological or smooth constraints in other contexts, such as sheaves of continuous or smooth sections of bundles) that the intuition of essentially independent fibres is quite an accurate one, at least if one avoids consideration of an uncountable number of objects simultaneously.

Example 3 (Extended Hilbert modules) This example is the one that motivated this post for me. Suppose that one has an extension ${(\tilde \Omega, \tilde {\mathcal B}, \tilde \mu)}$ of the base space ${(\Omega, {\mathcal B},\mu)}$ , thus we have a measurable factor map ${\pi: \tilde \Omega \rightarrow \Omega}$ such that the pushforward of the measure ${\tilde \mu}$ by ${\pi}$ is equal to ${\mu}$ . Then we have a conditional expectation operator ${\pi_*: L^2(\tilde \Omega,\tilde {\mathcal B},\tilde \mu) \rightarrow L^2(\Omega,{\mathcal B},\mu)}$ , defined as the adjoint of the pullback map ${\pi^*: L^2(\Omega,{\mathcal B},\mu) \rightarrow L^2(\tilde \Omega,\tilde {\mathcal B},\tilde \mu)}$ . As is well known, the conditional expectation operator also extends to a contraction ${\pi_*: L^1(\tilde \Omega,\tilde {\mathcal B},\tilde \mu) \rightarrow L^1(\Omega,{\mathcal B}, \mu)}$ ; by monotone convergence we may also extend ${\pi_*}$ to a map from measurable functions from ${\tilde \Omega}$ to the extended non-negative reals ${[0,+\infty]}$ , to measurable functions from ${\Omega}$ to ${[0,+\infty]}$ . We then define the “extended Hilbert module” ${L^2(\tilde \Omega|\Omega)}$ to be the space of functions ${f \in L^2(\tilde \Omega,\tilde {\mathcal B},\tilde \mu)}$ with ${\pi_*(|f|^2)}$ finite almost everywhere. This is an extended version of the Hilbert module ${L^\infty_{\Omega} L^2(\tilde \Omega|\Omega)}$ , which is defined similarly except that ${\pi_*(|f|^2)}$ is required to lie in ${L^\infty(\Omega,{\mathcal B},\mu)}$ ; this is a Hilbert module over ${L^\infty(\Omega, {\mathcal B}, \mu)}$ which is of particular importance in the Furstenberg-Zimmer structure theory of measure-preserving systems. We can then define the stochastic set ${L^2_\pi(\tilde \Omega)|\Omega}$ by setting

$\displaystyle \Gamma(L^2_\pi(\tilde \Omega)|E) := L^2( \pi^{-1}(E) | E )$

with the obvious restriction maps. In the case that ${\Omega,\Omega'}$ are standard Borel spaces, one can disintegrate ${\mu'}$ as an integral ${\mu' = \int_\Omega \nu_\omega\ d\mu(\omega)}$ of probability measures ${\nu_\omega}$ (supported in the fibre ${\pi^{-1}(\{\omega\})}$ ), in which case this stochastic set can be viewed as having fibres ${L^2( \tilde \Omega, \tilde {\mathcal B}, \nu_\omega )}$ (though if ${\Omega}$ is not discrete, there are still some measurability conditions in ${\omega}$ on the local and global elements that need to be imposed). However, I am interested in the case when ${\Omega,\Omega'}$ are not standard Borel spaces (in fact, I will take them to be algebraic probability spaces, as defined in this previous post), in which case disintegrations are not available. However, it appears that the stochastic analysis developed in this blog post can serve as a substitute for the tool of disintegration in this context.

We make the remark that if ${X|\Omega}$ is a stochastic set and ${E, F}$ are events that are equivalent up to null events, then one can identify ${\Gamma(X|E)}$ with ${\Gamma(X|F)}$ (through their common restriction to ${\Gamma(X|(E \cap F))}$ , with the restriction maps now being bijections). As such, the notion of a stochastic set does not require the full structure of a concrete probability space ${(\Omega, {\mathcal B}, {\mathbf P})}$ ; one could also have defined the notion using only the abstract ${\sigma}$ -algebra consisting of ${{\mathcal B}}$ modulo null events as the base space, or equivalently one could define stochastic sets over the algebraic probability spaces defined in this previous post. However, we will stick with the classical formalism of concrete probability spaces here so as to keep the notation reasonably familiar.

As a corollary of the above observation, we see that if the base space ${\Omega}$ has total measure ${0}$ , then all stochastic sets are trivial (they are just points).

Exercise 2 If ${X|\Omega}$ is a stochastic set, show that there exists an event ${\Omega'}$ with the property that for any event ${E}$ , ${\Gamma(X|E)}$ is non-empty if and only if ${E}$ is contained in ${\Omega'}$ modulo null events. (In particular, ${\Omega'}$ is unique up to null events.) Hint: consider the numbers ${\mu( E )}$ for ${E}$ ranging over all events with ${\Gamma(X|E)}$ non-empty, and form a maximising sequence for these numbers. Then use all three axioms of a stochastic set.

One can now start take many of the fundamental objects, operations, and results in set theory (and, hence, in most other categories of mathematics) and establish analogues relative to a finite measure space. Implicitly, what we will be doing in the next few paragraphs is endowing the category of stochastic sets with the structure of an elementary topos. However, to keep things reasonably concrete, we will not explicitly emphasise the topos-theoretic formalism here, although it is certainly lurking in the background.

Firstly, we define a stochastic function ${f: X|\Omega \rightarrow Y|\Omega}$ between two stochastic sets ${X|\Omega, Y|\Omega}$ to be a collection of maps ${f: \Gamma(X|E) \rightarrow \Gamma(Y|E)}$ for each ${E \in {\mathcal B}}$ which form a natural transformation in the sense that ${f(x|E) = f(x)|E}$ for all ${x \in \Gamma(X|F)}$ and nested events ${E \subset F}$ . In the case when ${\Omega}$ is discrete and at most countable (and after deleting all null points), a stochastic function is nothing more than a collection of functions ${f_\omega: X_\omega \rightarrow Y_\omega}$ for each ${\omega \in \Omega}$ , with the function ${f: \Gamma(X|E) \rightarrow \Gamma(Y|E)}$ then being a direct sum of the factor functions ${f_\omega}$ :

$\displaystyle f( (x_\omega)_{\omega \in E} ) = ( f_\omega(x_\omega) )_{\omega \in E}.$

Thus (in the discrete, at most countable setting, at least) stochastic functions do not mix together information from different states ${\omega}$ in a sample space; the value of ${f(x)}$ at ${\omega}$ depends only on the value of ${x}$ at ${\omega}$ . The situation is a bit more subtle for continuous probability spaces, due to the identification of stochastic objects that agree almost surely, nevertheness it is still good intuition to think of stochastic functions as essentially being “pointwise” or “local” in nature.

One can now form the stochastic set ${\hbox{Hom}(X \rightarrow Y)|\Omega}$ of functions from ${X|\Omega}$ to ${Y|\Omega}$ , by setting ${\Gamma(\hbox{Hom}(X \rightarrow Y)|E)}$ for any event ${E}$ to be the set of local stochastic functions ${f: X|E \rightarrow Y|E}$ of the localisations of ${X|\Omega, Y|\Omega}$ to ${E}$ ; this is a stochastic set if we use the obvious restriction maps. In the case when ${\Omega}$ is discrete and at most countable, the fibre ${\hbox{Hom}(X \rightarrow Y)_\omega}$ at a point ${\omega}$ of positive measure is simply the set ${Y_\omega^{X_\omega}}$ of functions from ${X_\omega}$ to ${Y_\omega}$ .

In a similar spirit, we say that one stochastic set ${Y|\Omega}$ is a (stochastic) subset of another ${X|\Omega}$ , and write ${Y|\Omega \subset X|\Omega}$ , if we have a stochastic inclusion map, thus ${\Gamma(Y|E) \subset \Gamma(X|E)}$ for all events ${E}$ , with the restriction maps being compatible. We can then define the power set ${2^X|\Omega}$ of a stochastic set ${X|\Omega}$ by setting ${\Gamma(2^X|E)}$ for any event ${E}$ to be the set of all stochastic subsets ${Y|E}$ of ${X|E}$ relative to ${E}$ ; it is easy to see that ${2^X|\Omega}$ is a stochastic set with the obvious restriction maps (one can also identify ${2^X|\Omega}$ with ${\hbox{Hom}(X, \{\hbox{true},\hbox{false}\})|\Omega}$ in the obvious fashion). Again, when ${\Omega}$ is discrete and at most countable, the fibre of ${2^X|\Omega}$ at a point ${\omega}$ of positive measure is simply the deterministic power set ${2^{X_\omega}}$ .

Note that if ${f: X|\Omega \rightarrow Y|\Omega}$ is a stochastic function and ${Y'|\Omega}$ is a stochastic subset of ${Y|\Omega}$ , then the inverse image ${f^{-1}(Y')|\Omega}$ , defined by setting ${\Gamma(f^{-1}(Y')|E)}$ for any event ${E}$ to be the set of those ${x \in \Gamma(X|E)}$ with ${f(x) \in \Gamma(Y'|E)}$ , is a stochastic subset of ${X|\Omega}$ . In particular, given a ${k}$ -ary relation ${R: X_1 \times \dots \times X_k|\Omega \rightarrow \{\hbox{true}, \hbox{false}\}|\Omega}$ , the inverse image ${R^{-1}( \{ \hbox{true} \}|\Omega )}$ is a stochastic subset of ${X_1 \times \dots \times X_k|\Omega}$ , which by abuse of notation we denote as

$\displaystyle \{ (x_1,\dots,x_k) \in X_1 \times \dots \times X_k: R(x_1,\dots,x_k) \hbox{ is true} \}|\Omega.$

In a similar spirit, if ${X'|\Omega}$ is a stochastic subset of ${X|\Omega}$ and ${f: X|\Omega \rightarrow Y|\Omega}$ is a stochastic function, we can define the image ${f(X')|\Omega}$ by setting ${\Gamma(f(X')|E)}$ to be the set of those ${f(x)}$ with ${x \in \Gamma(X'|E)}$ ; one easily verifies that this is a stochastic subset of ${Y|\Omega}$ .

Remark 2 One should caution that in the definition of the subset relation ${Y|\Omega \subset X|\Omega}$ , it is important that ${\Gamma(Y|E) \subset \Gamma(X|E)}$ for all events ${E}$ , not just the global event ${\Omega}$ ; in particular, just because a stochastic set ${X|\Omega}$ has no global sections, does not mean that it is contained in the stochastic empty set ${\emptyset|\Omega}$ .

Now we discuss Boolean operations on stochastic subsets of a given stochastic set ${X|\Omega}$ . Given two stochastic subsets ${X_1|\Omega, X_2|\Omega}$ of ${X|\Omega}$ , the stochastic intersection ${(X_1 \cap X_2)|\Omega}$ is defined by setting ${\Gamma((X_1 \cap X_2)|E)}$ to be the set of ${x \in \Gamma(X|E)}$ that lie in both ${\Gamma(X_1|E)}$ and ${\Gamma(X_2|E)}$ :

$\displaystyle \Gamma(X_1 \cap X_2)|E) := \Gamma(X_1|E) \cap \Gamma(X_2|E).$

This is easily verified to again be a stochastic subset of ${X|\Omega}$ . More generally one may define stochastic countable intersections ${(\bigcap_{n=1}^\infty X_n)|\Omega}$ for any sequence ${X_n|\Omega}$ of stochastic subsets of ${X|\Omega}$ . One could extend this definition to uncountable families if one wished, but I would advise against it, because some of the usual laws of Boolean algebra (e.g. the de Morgan laws) may break down in this setting.

Stochastic unions are a bit more subtle. The set ${\Gamma((X_1 \cup X_2)|E)}$ should not be defined to simply be the union of ${\Gamma(X_1|E)}$ and ${\Gamma(X_2|E)}$ , as this would not respect the gluing axiom. Instead, we define ${\Gamma((X_1 \cup X_2)|E)}$ to be the set of all ${x \in \Gamma(X|E)}$ such that one can cover ${E}$ by measurable subevents ${E_1,E_2}$ such that ${x_i|E_i \in \Gamma(X_i|E_i)}$ for ${i=1,2}$ ; then ${(X_1 \cup X_2)|\Omega}$ may be verified to be a stochastic subset of ${X|\Omega}$ . Thus for instance ${\{0,1\}|\Omega}$ is the stochastic union of ${\{0\}|\Omega}$ and ${\{1\}|\Omega}$ . Similarly for countable unions ${(\bigcup_{n=1}^\infty X_n)|\Omega}$ of stochastic subsets ${X_n|\Omega}$ of ${X|\Omega}$ , although for uncountable unions are extremely problematic (they are disliked by both the measure theory and the countable gluing axiom) and will not be defined here. Finally, the stochastic difference set ${\Gamma((X_1 \backslash X_2)|E)}$ is defined as the set of all ${x|E}$ in ${\Gamma(X_1|E)}$ such that ${x|F \not \in \Gamma(X_2|F)}$ for any subevent ${F}$ of ${E}$ of positive probability. One may verify that in the case when ${\Omega}$ is discrete and at most countable, these Boolean operations correspond to the classical Boolean operations applied separately to each fibre ${X_{i,\omega}}$ of the relevant sets ${X_i}$ . We also leave as an exercise to the reader to verify the usual laws of Boolean arithmetic, e.g. the de Morgan laws, provided that one works with at most countable unions and intersections.

One can also consider a stochastic finite union ${(\bigcup_{n=1}^N X_n)|\Omega}$ in which the number ${N}$ of sets in the union is itself stochastic. More precisely, let ${X|\Omega}$ be a stochastic set, let ${N \in {\bf N}|\Omega}$ be a stochastic natural number, and let ${n \mapsto X_n|\Omega}$ be a stochastic function from the stochastic set ${\{ n \in {\bf N}: n \leq N\}|\Omega}$ (defined by setting ${\Gamma(\{n \in {\bf N}: n\leq N\}|E) := \{ n \in {\bf N}|E: n \leq N|E\}}$ )) to the stochastic power set ${2^X|\Omega}$ . Here we are considering ${0}$ to be a natural number, to allow for unions that are possibly empty, with ${{\bf N}_+ := {\bf N} \backslash \{0\}}$ used for the positive natural numbers. We also write ${(X_n)_{n=1}^N|\Omega}$ for the stochastic function ${n \mapsto X_n|\Omega}$ . Then we can define the stochastic union ${\bigcup_{n=1}^N X_n|\Omega}$ by setting ${\Gamma(\bigcup_{n=1}^N X_n|E)}$ for an event ${E}$ to be the set of local elements ${x \in \Gamma(X|E)}$ with the property that there exists a covering of ${E}$ by measurable subevents ${E_{n_0}}$ for ${n_0 \in {\bf N}_+}$ , such that one has ${n_0 \leq N|E_{n_0}}$ and ${x|E_{n_0} \in \Gamma(X_{n_0}|E_{n_0})}$ . One can verify that ${\bigcup_{n=1}^N X_n|\Omega}$ is a stochastic set (with the obvious restriction maps). Again, in the model case when ${\Omega}$ is discrete and at most countable, the fibre ${(\bigcup_{n=1}^N X_n)_\omega}$ is what one would expect it to be, namely ${\bigcup_{n=1}^{N(\omega)} (X_n)_\omega}$ .

The Cartesian product ${(X \times Y)|\Omega}$ of two stochastic sets may be defined by setting ${\Gamma((X \times Y)|E) := \Gamma(X|E) \times \Gamma(Y|E)}$ for all events ${E}$ , with the obvious restriction maps; this is easily seen to be another stochastic set. This lets one define the concept of a ${k}$ -ary operation ${f: (X_1 \times \dots \times X_k)|\Omega \rightarrow Y|\Omega}$ from ${k}$ stochastic sets ${X_1,\dots,X_k}$ to another stochastic set ${Y}$ , or a ${k}$ -ary relation ${R: (X_1 \times \dots \times X_k)|\Omega \rightarrow \{\hbox{true}, \hbox{false}\}|\Omega}$ . In particular, given ${x_i \in X_i|\Omega}$ for ${i=1,\dots,k}$ , the relation ${R(x_1,\dots,x_k)}$ may be deterministically true, deterministically false, or have some other stochastic truth value.

Remark 3 In the degenerate case when ${\Omega}$ is null, stochastic logic becomes a bit weird: all stochastic statements are deterministically true, as are their stochastic negations, since every event in ${\Omega}$ (even the empty set) now holds with full probability. Among other pathologies, the empty set now has a global element over ${\Omega}$ (this is analogous to the notorious convention ${0^0=1}$ ), and any two deterministic objects ${x,y}$ become equal over ${\Omega}$ : ${x|\Omega=y|\Omega}$ .

The following simple observation is crucial to subsequent discussion. If ${(x_n)_{n \in {\bf N}_+}}$ is a sequence taking values in the global elements ${\Gamma(X|\Omega)}$ of a stochastic space ${X|\Omega}$ , then we may also define global elements ${x_n \in \Gamma(X|\Omega)}$ for stochastic indices ${n \in {\bf N}_+|\Omega}$ as well, by appealing to the countable gluing axiom to glue together ${x_{n_0}}$ restricted to the set ${\{ \omega \in \Omega: n(\omega) = n_0\}}$ for each deterministic natural number ${n_0}$ to form ${x_n}$ . With this definition, the map ${n \mapsto x_n}$ is a stochastic function from ${{\bf N}_+|\Omega}$ to ${X|\Omega}$ ; indeed, this creates a one-to-one correspondence between external sequences (maps ${n \mapsto x_n}$ from ${{\bf N}_+}$ to ${\Gamma(X|\Omega)}$ ) and stochastic sequences (stochastic functions ${n \mapsto x_n}$ from ${{\bf N}_+|\Omega}$ to ${X|\Omega}$ ). Similarly with ${{\bf N}_+}$ replaced by any other at most countable set. This observation will be important in allowing many deterministic arguments involving sequences will be able to be carried over to the stochastic setting.

We now specialise from the extremely broad discipline of set theory to the more focused discipline of real analysis. There are two fundamental axioms that underlie real analysis (and in particular distinguishes it from real algebra). The first is the Archimedean property, which we phrase in the “no infinitesimal” formulation as follows:

Proposition 2 (Archimedean property) Let ${x \in {\bf R}}$ be such that ${x \leq 1/n}$ for all positive natural numbers ${n}$ . Then ${x \leq 0}$ .

The other is the least upper bound axiom:

Proposition 3 (Least upper bound axiom) Let ${S}$ be a non-empty subset of ${{\bf R}}$ which has an upper bound ${M \in {\bf R}}$ , thus ${x \leq M}$ for all ${x \in S}$ . Then there exists a unique real number ${\sup S \in {\bf R}}$ with the following properties:

${x \leq \sup S}$ for all ${x \in S}$ .

For any real ${L < \sup S}$ , there exists ${x \in S}$ such that ${L < x \leq \sup S}$ .

${\sup S \leq M}$ .

Furthermore, ${\sup S}$ does not depend on the choice of ${M}$ .

The Archimedean property extends easily to the stochastic setting:

Proposition 4 (Stochastic Archimedean property) Let ${x \in \Gamma({\bf R}|\Omega)}$ be such that ${x \leq 1/n}$ for all deterministic natural numbers ${n}$ . Then ${x \leq 0}$ .

Remark 4 Here, incidentally, is one place in which this stochastic formalism deviates from the nonstandard analysis formalism, as the latter certainly permits the existence of infinitesimal elements. On the other hand, we caution that stochastic real numbers are permitted to be unbounded, so that formulation of Archimedean property is not valid in the stochastic setting.

The proof is easy and is left to the reader. The least upper bound axiom also extends nicely to the stochastic setting, but the proof requires more work (in particular, our argument uses the monotone convergence theorem):

Theorem 5 (Stochastic least upper bound axiom) Let ${S|\Omega}$ be a stochastic subset of ${{\bf R}|\Omega}$ which has a global upper bound ${M \in {\bf R}|\Omega}$ , thus ${x \leq M}$ for all ${x \in \Gamma(S|\Omega)}$ , and is globally non-empty in the sense that there is at least one global element ${x \in \Gamma(S|\Omega)}$ . Then there exists a unique stochastic real number ${\sup S \in \Gamma({\bf R}|\Omega)}$ with the following properties:

${x \leq \sup S}$ for all ${x \in \Gamma(S|\Omega)}$ .

For any stochastic real ${L < \sup S}$ , there exists ${x \in \Gamma(S|\Omega)}$ such that ${L < x \leq \sup S}$ .

${\sup S \leq M}$ .

Furthermore, ${\sup S}$ does not depend on the choice of ${M}$ .

For future reference, we note that the same result holds with ${{\bf R}}$ replaced by ${{\bf N} \cup \{+\infty\}}$ throughout, since the latter may be embedded in the former, for instance by mapping ${n}$ to ${1 - \frac{1}{n+1}}$ and ${+\infty}$ to ${1}$ . In applications, the above theorem serves as a reasonable substitute for the countable axiom of choice, which does not appear to hold in unrestricted generality relative to a measure space; in particular, it can be used to generate various extremising sequences for stochastic functionals on various stochastic function spaces.

Proof: Uniqueness is clear (using the Archimedean property), as well as the independence on ${M}$ , so we turn to existence. By using an order-preserving map from ${{\bf R}}$ to ${(-1,1)}$ (e.g. ${x \mapsto \frac{2}{\pi} \hbox{arctan}(x)}$ ) we may assume that ${S|\Omega}$ is a subset of ${(-1,1)|\Omega}$ , and that ${M < 1}$ .

We observe that ${\Gamma(S|\Omega)}$ is a lattice: if ${x, y \in \Gamma(S|\Omega)}$ , then ${\max(x,y)}$ and ${\min(x,y)}$ also lie in ${\Gamma(S|\Omega)}$ . Indeed, ${\max(x,y)}$ may be formed by appealing to the countable gluing axiom to glue ${y}$ (restricted the set ${\{ \omega \in \Omega: x(\omega) < y(\omega) \}}$ ) with ${x}$ (restricted to the set ${\{ \omega \in \Omega: x(\omega) \geq y(\omega) \}}$ ), and similarly for ${\min(x,y)}$ . (Here we use the fact that relations such as ${<}$ are Borel measurable on ${{\bf R}}$ .)

Let ${A \in {\bf R}}$ denote the deterministic quantity

$\displaystyle A := \sup \{ \int_\Omega x(\omega)\ d\mu(\omega): x \in \Gamma(S|\Omega) \}$

then (by Proposition 3!) ${A}$ is well-defined; here we use the hypothesis that ${\mu(\Omega)}$ is finite. Thus we may find a sequence ${(x_n)_{n \in {\bf N}}}$ of elements ${x_n}$ of ${\Gamma(S|\Omega)}$ such that

$\displaystyle \int_\Omega x_n(\omega)\ d\mu(\omega) \rightarrow A \hbox{ as } n \rightarrow \infty. \ \ \ \ \ (1)$

Using the lattice property, we may assume that the ${x_n}$ are non-decreasing: ${x_n \leq x_m}$ whenever ${n \leq m}$ . If we then define ${\sup S(\omega) := \sup_n x_n(\omega)}$ (after choosing measurable representatives of each equivalence class ${x_n}$ ), then ${\sup S}$ is a stochastic real with ${\sup S \leq M}$ .

If ${x \in \Gamma(S|\Omega)}$ , then ${\max(x,x_n) \in \Gamma(S|\Omega)}$ , and so

$\displaystyle \int_\Omega \max(x,x_n)\ d\mu(\omega) \leq A.$

From this and (1) we conclude that

$\displaystyle \int_\Omega \max(x-x_n,0) \rightarrow 0 \hbox{ as } n \rightarrow \infty.$

From monotone convergence, we conclude that

$\displaystyle \int_\Omega \max(x-\sup S,0) = 0$

and so ${x \leq \sup S}$ , as required.

Now let ${L < \sup S}$ be a stochastic real. After choosing measurable representatives of each relevant equivalence class, we see that for almost every ${\omega \in \Omega}$ , we can find a natural number ${n(\omega)}$ with ${x_{n(\omega)} > L}$ . If we choose ${n(\omega)}$ to be the first such positive natural number when it exists, and (say) ${1}$ otherwise, then ${n}$ is a stochastic positive natural number and ${L < x_n}$ . The claim follows. $\Box$

Remark 5 One can abstract away the role of the measure ${\mu}$ here, leaving only the ideal of null sets. The property that the measure is finite is then replaced by the more general property that given any non-empty family of measurable sets, there is an at most countable union of sets in that family that is an upper bound modulo null sets for all elements in that faily.

Using Proposition 4 and Theorem 5, one can then revisit many of the other foundational results of deterministic real analysis, and develop stochastic analogues; we give some examples of this below the fold (focusing on the Heine-Borel theorem and a case of the spectral theorem). As an application of this formalism, we revisit some of the Furstenberg-Zimmer structural theory of measure-preserving systems, particularly that of relatively compact and relatively weakly mixing systems, and interpret them in this framework, basically as stochastic versions of compact and weakly mixing systems (though with the caveat that the shift map is allowed to act non-trivially on the underlying probability space). As this formalism is “point-free”, in that it avoids explicit use of fibres and disintegrations, it will be well suited for generalising this structure theory to settings in which the underlying probability spaces are not standard Borel, and the underlying groups are uncountable; I hope to discuss such generalisations in future blog posts.

Remark 6 Roughly speaking, stochastic real analysis can be viewed as a restricted subset of classical real analysis in which all operations have to be “measurable” with respect to the base space. In particular, indiscriminate application of the axiom of choice is not permitted, and one should largely restrict oneself to performing countable unions and intersections rather than arbitrary unions or intersections. Presumably one can formalise this intuition with a suitable “countable transfer principle”, but I was not able to formulate a clean and general principle of this sort, instead verifying various assertions about stochastic objects by hand rather than by direct transfer from the deterministic setting. However, it would be desirable to have such a principle, since otherwise one is faced with the tedious task of redoing all the foundations of real analysis (or whatever other base theory of mathematics one is going to be working in) in the stochastic setting by carefully repeating all the arguments.

More generally, topos theory is a good formalism for capturing precisely the informal idea of performing mathematics with certain operations, such as the axiom of choice, the law of the excluded middle, or arbitrary unions and intersections, being somehow “prohibited” or otherwise “restricted”.

— 1. Metric spaces relative to a finite measure space —

The definition of a metric space carries over in the obvious fashion to the stochastic setting:

Definition 6 (Stochastic metric spaces) A stochastic metric space ${X|\Omega = (X|\Omega,d)}$ is defined to be a stochastic set ${X|\Omega}$ , together with a stochastic function ${d: X|\Omega \times X|\Omega \rightarrow [0,+\infty)|\Omega}$ that obeys the following axioms for each event ${\Omega'}$ :

(Non-degeneracy) If ${x,y \in X|\Omega'}$ , then ${d(x,y)=0}$ if and only if ${x=y}$ .

(Symmetry) If ${x,y \in X|\Omega'}$ , then ${d(x,y) = d(y,x)}$ .

(Triangle inequality) If ${x,y,z \in X|\Omega'}$ , then ${d(x,z) \leq d(x,y)+d(y,z)}$ .

Remark 7 One could potentially interpret the non-degeneracy axiom in two ways; either deterministically ( ${d(x,y)=0}$ is deterministically true if and only if ${x=y}$ is deterministically true) or stochastically (“ ${d(x,y)=0}$ if and only if ${x=y}$ ” is deterministically true). However, it is easy to see by a gluing argument that the two interpretations are logically equivalent. Also, if ${X|\Omega}$ is globally non-empty, then one only needs to verify the metric space axioms for ${\Omega'=\Omega}$ , as one can then obtain the ${\Omega' \subsetneq \Omega}$ cases by gluing with a global section on ${\Omega \backslash \Omega'}$ . However, when ${X|\Omega}$ has no global elements, it becomes necessary to work locally.

Note that if ${(X,d)}$ is a deterministic measurable metric space (thus ${X}$ is a measurable space equipped with a measurable metric ${d}$ ), then its stochastic counterpart ${(X|\Omega, d)}$ is a stochastic metric space. (As usual, we do not attempt to interpret ${(X|\Omega, d)}$ when there is no measurable structure present for ${X}$ .) In the case of a discrete at most countable ${\Omega}$ (and after deleting any points of measure zero), a stochastic metric space ${(X|\Omega,d)}$ is essentially just a bundle ${(X_\omega,d_\omega)_{\omega \in \Omega}}$ of metric spaces, with no relations constraining these metric spaces with each other (for instance, the cardinality of ${X_\omega}$ may vary arbitrarily with ${\omega}$ ).

We extend the notion of convergence in stochastic metric spaces:

Definition 7 (Stochastic convergence) Let ${X|\Omega = (X|\Omega,d)}$ be a stochastic metric space, and let ${(x_n)_{n \in {\bf N}_+}}$ be a sequence in ${\Gamma(X|\Omega)}$ (which, as discussed earlier, may be viewed as a stochastic function ${n \mapsto x_n}$ from ${{\bf N}_+|\Omega}$ to ${X|\Omega}$ ). Let ${x}$ be an element of ${\Gamma(X|\Omega)}$ .

We say that ${x_n}$ stochastically converges to ${x}$ if, for every stochastic real ${\epsilon>0}$ , there exists a stochastic positive natural number ${N \in {\bf N}_+|\Omega}$ such that ${d(x_n,x) < \epsilon}$ for all stochastic positive natural numbers ${n \in {\bf N}_+|\Omega}$ with ${n \geq N}$ .

We say that ${x_n}$ is stochastically Cauchy if, for every stochastic real ${\epsilon>0}$ , there exists a stochastic natural number ${N \in {\bf N}_+|\Omega}$ such that ${d(x_n,x_m) < \epsilon}$ for all stochastic natural numbers ${n,m \in {\bf N}_+|\Omega}$ with ${n,m \geq N}$ .

We say that ${X|\Omega}$ is stochastically complete if every stochastically Cauchy sequence is stochastically convergent, and furthermore for any event ${\Omega'}$ in ${\Omega}$ , any stochastically Cauchy sequence relative to ${\Omega'}$ is stochastically convergent relative to ${\Omega'}$ .

As usual, the additional localisation in the definition of stochastic completeness to an event ${\Omega'}$ is needed to avoid a stochastic set being stochastically complete for the trivial reason that one of its fibres happens to be empty, so that there are no global elements of the stochastic set, only local elements. (This localisation is not needed for the notions of stochastic convergence or the stochastic Cauchy property, as these automatically are preserved by localisation.)

Exercise 3 Show that to verify stochastic convergence, it suffices to restrict attention to errors ${\epsilon}$ of the form ${\epsilon = 1/m}$ for deterministic positive natural numbers ${m}$ . Similarly for the stochastically Cauchy property.

Exercise 4 Let ${X}$ be a measurable metric space. Show that ${X|\Omega}$ is stochastically complete if and only if ${X}$ is complete. Thus for instance ${{\bf R}|\Omega}$ is stochastically complete.

In the case when ${\Omega}$ is discrete and at most countable, or when ${X|\Omega}$ is the stochastic version of a deterministic measurable space ${X}$ , stochastic convergence is just the familiar notion of almost sure convergence: ${x_n \in \Gamma(X|\Omega)}$ converges stochastically to ${x \in \Gamma(X|\Omega)}$ if and only if, for almost every ${\omega \in \Omega}$ , ${x_n(\omega)}$ converges to ${x(\omega)}$ in ${X_\omega}$ . There is no uniformity of convergence in the ${\omega}$ parameter; such a uniformity could be imposed by requiring the quantity ${N}$ in the above definition to be a deterministic natural number rather than a stochastic one, but we will not need this notion here. Similarly for the stochastic Cauchy property. Stochastic completeness in this context is then equivalent to completeness of ${X_\omega}$ for each ${\omega}$ that occurs with positive probability. (As noted previously, it is important here that we define stochastic completeness with localisation, in case some of the fibres ${X_\omega}$ are empty.)

In a stochastic metric space ${X|\Omega}$ , we can form the balls ${B(x,r)|\Omega}$ for any ${x \in \Gamma(X|\Omega)}$ and stochastic real ${r>0}$ , by setting ${\Gamma(B(x,r)|E)}$ to be the set of all ${y \in \Gamma(X|E)}$ such that ${d(x,y) < r}$ locally on ${E}$ ; these are stochastic subsets of ${X|\Omega}$ (indeed, ${B(x,r)}$ is the inverse image of ${\{ r' \in [0,+\infty): r' < r \}|\Omega}$ under the pinned distance map ${y \mapsto d(x,y)}$ ).

By chasing the definitions, we see that if ${(x_n)_{n \in {\bf N}_+}}$ is a sequence of elements ${x_n \in \Gamma(X|\Omega)}$ of a stochastic metric space ${X|\Omega}$ , and ${x}$ is an element of ${\Gamma(X|\Omega)}$ , then ${x_n}$ stochastically converges to ${x}$ if and only if, for every stochastic ${\epsilon>0}$ , there exists a stochastic natural positive number ${N \in \Gamma({\bf N}_+|\Omega)}$ such that ${x_n \in \Gamma(B(x,\epsilon)|\Omega)}$ for all stochastic positive natural numbers ${n \geq N}$ .

Given a sequence ${(x_n)_{n \in {\bf N}_+}}$ of elements ${x_n \in \Gamma(X|\Omega)}$ of a stochastic metric space ${X|\Omega}$ , we define a stochastic subsequence ${(x_{n_j})_{j \in {\bf N}_+}}$ to be a sequence of the form ${j \mapsto x_{n_j}}$ , where ${(n_j)_{j \in {\bf N}_+}}$ is a sequence of stochastic natural numbers ${n_j \in {\bf N}_+|\Omega}$ , which stochastically go to infinity in the following sense: for every stochastic positive natural number ${N \in \Gamma({\bf N}_+|\Omega)}$ , there exists a stochastic positive natural number ${J}$ such that ${n_j \geq N}$ for all stochastic positive natural numbers ${j \geq J}$ . Note that when ${\Omega}$ is discrete and at most countable, this operation corresponds to selecting a subsequence ${(x_{n_j(\omega),\omega})_{j \in {\bf N}_+}}$ of ${(x_{n,\omega})_{n \in {\bf N}_+}}$ for each ${\omega}$ occurring with positive probability, with the indices ${n_j(\omega)}$ of the subsequence permitted to vary in ${\omega}$ .

Exercise 5 Let ${(x_n)_{n \in{\bf N}_+}}$ be a sequence of elements ${\Gamma(X|\Omega)}$ of a stochastic metric space ${X|\Omega}$ , and let ${x \in \Gamma(X|\Omega)}$ .

(i) Show that ${x_n}$ can converge stochastically to at most one element of ${\Gamma(X|\Omega)}$ .

(ii) Show that if ${x_n}$ converges stochastically to ${x}$ , then every stochastic subsequence ${(x_{n_j})_{j \in {\bf N}_+}}$ also converges stochastically to ${x}$ .

(iii) Show that if ${x_n}$ is stochastically Cauchy, and some stochastic subsequence of ${x_n}$ converges stochastically to ${x}$ , then the entire sequence ${x_n}$ converges stochastically to ${x}$ .

(iv) Show that there exists an event ${E}$ , unique up to null events, with the property that ${x_n|E}$ converges stochastically to ${x|E}$ , and that there exists a stochastic ${\epsilon>0}$ over the complement ${E^c}$ of ${E}$ , with the property that for any stochastic natural number ${N|E^c}$ on ${E^c}$ , there exists ${n|E^c \geq N|E^c}$ such that ${d(x,x_n)|E^c \geq \epsilon}$ . (Informally, ${E}$ is the set of states for which ${x_n}$ converges to ${x}$ ; the key point is that this set is automatically measurable.)

(v) (Urysohn subsequence principle) Show that ${x_n}$ converges stochastically to ${x}$ if and only if every stochastic subsequence ${(x_{n_j})_{j \in {\bf N}_+}}$ of ${(x_n)_{n \in {\bf N}_+}}$ has a further stochastic subsequence ${(x_{n_{j_k}})_{k \in {\bf N}_+}}$ that converges stochastically to ${x}$ .

(Hint: All of these exercises can be established through consideration of the events ${E_{n,k}}$ for ${n,k \in {\bf N}_+}$ , defined up to null events as the event that ${d( x_n, x ) < \frac{1}{k}}$ holds stochastically.)

Next, we define the stochastic counterpart of total boundedness.

Definition 8 (Total boundedness) A stochastic metric space ${X|\Omega}$ is said to be stochastically totally bounded if, for every stochastic real ${\epsilon>0}$ , there exists a stochastic natural number ${N \in {\bf N}|\Omega}$ and a stochastic function ${n \mapsto x_n}$ from the stochastic set ${\{ n \in {\bf N}_+: n \leq N \}|\Omega}$ to ${X|\Omega}$ , such that

$\displaystyle X|\Omega = \bigcup_{n=1}^N B(x_n,\epsilon)|\Omega.$

(Note that we allow ${N}$ to be zero locally or globally; thus for instance the empty set ${\emptyset|\Omega}$ is considered to be totally bounded.) We will denote this stochastic function ${n \mapsto x_n}$ as ${(x_n)_{n=1}^N|\Omega}$ .

Exercise 6 If ${\Omega}$ is discrete and at most countable, show that ${X|\Omega}$ is stochastically totally bounded if and only if for each ${\omega}$ of positive probability, the fibre ${X_\omega}$ is totally bounded in the deterministic sense.

Exercise 7 Show that to verify the stochastic total boundedness of a stochastic metric space, it suffices to do so for parameters ${\epsilon}$ of the form ${\epsilon=1/k}$ for some deterministic positive natural number ${k}$ .

We have a stochastic version of (a fragment of) the Heine-Borel theorem:

Theorem 9 (Stochastic Heine-Borel theorem) Let ${X|\Omega}$ be a stochastic metric space. Then the following are equivalent:

(i) ${X|\Omega}$ is stochastically complete and stochastically totally bounded.

(ii) Every sequence in ${\Gamma(X|\Omega)}$ has a stochastic subsequence that is stochastically convergent. Furthermore, for any event ${\Omega'}$ , every sequence in ${\Gamma(X|\Omega')}$ has a stochastic subsequence that is stochastically convergent relative to ${\Omega'}$ .

As with the definition of stochastic completeness, the second part of (ii) is necessary: if for instance ${\Omega}$ is discrete and countable, and one of the fibres ${X_\omega}$ happens to be empty, then there are no global elements of ${X|\Omega}$ and the first part of (ii) becomes trivially true, even if other fibres of ${X_\omega}$ fail to be complete or totally bounded.

Inspired by the above theorem, we will call a stochastic metric space ${X|\Omega}$ stochastically compact if (i) or (ii) holds. Note that this only recovers a fragment of the deterministic Heine-Borel theorem, as the characterisation of compactness in terms of open covers is missing. I was not able to set up a characterisation of this form, since one was only allowed to use countable unions; but perhaps some version of this characterisation can be salvaged.

Proof: The basic idea here is to mimic the classical proof of this fragment of the Heine-Borel theorem, taking care to avoid any internal appeal to the countable axiom of choice in order to keep everything measurable. (However, we can and will use the axiom of countable choice externally in the ambient set theory.)

Suppose first that ${X|\Omega}$ fails to be stochastically complete. Then we can find an event ${\Omega'}$ and a stochastically Cauchy sequence ${x_n \in \Gamma(X|\Omega')}$ for ${n \in {\bf N}}$ that fails to be stochastically convergent in ${\Gamma(X|\Omega')}$ . By Exercise 5, no stochastic subsequence of ${x_n}$ can be stochastically convergent in ${X|\Omega'}$ either, and so (ii) fails.

Now suppose that ${X|\Omega}$ fails to be stochastically bounded. Then one can find a stochastic real number ${\epsilon>0}$ , such that it is not possible to find any stochastic natural number ${N \in \Gamma({\bf N}|\Omega)}$ and a stochastic sequence ${(x_n)_{n=1}^N|\Omega}$ (that is, a stochastic function ${n \mapsto x_n}$ from ${\{ n \in {\bf N}_+: n \leq N \}|\Omega}$ to ${X|\Omega}$ ), such that

$\displaystyle X|\Omega = \bigcup_{n=1}^N B(x_n,\epsilon)|\Omega.$

(By Exercise 7 one could take ${\epsilon=1/k}$ for a deterministic positive natural ${k}$ , but we will not need to do so here.)

Let ${S}$ be the set of those ${N \in \Gamma({\bf N}|\Omega)}$ for which one can find a stochastic sequence ${(x_n)_{n=1}^N|\Omega}$ which is ${\epsilon}$ -separated in the sense that ${d(x_n,x_m) \geq \epsilon}$ for all distinct ${n,m \in {\bf N}_+|\Omega}$ with ${n,m \leq N}$ , and more generally for any event ${\Omega'}$ , that ${d(x_n,x_m) \geq \epsilon}$ relative to ${\Omega'}$ for all distinct ${n,m \in{\bf N}_+|\Omega'}$ with ${n,m \leq N|\Omega'}$ . (We need to relativise to ${\Omega'}$ here to properly manage the case that ${N}$ sometimes vanishes.) It is easy to see that ${S}$ can be given the structure of a stochastic subset of ${{\bf N}|\Omega}$ , and contains ${0|\Omega}$ . By Theorem 5, there is thus a well-defined supremum ${\sup S \in ({\bf N} \cup \{+\infty\})|\Omega}$ . We claim that ${\sup S}$ is stochastically infinite with positive probability. Suppose for contradiction that this were not the case, then ${\sup S \in {\bf N}|\Omega}$ . By definition of supremum (taking ${L = \max(\sup S - 1, 0)}$ in Theorem 5), we conclude that ${\sup S \in S}$ , thus there exists a stochastic sequence ${(x_n)_{n=1}^{\sup S}|\Omega}$ which is ${\epsilon}$ -separated. We now claim that

$\displaystyle X|\Omega = \bigcup_{n=1}^{\sup S} B(x_n,\epsilon)|\Omega, \ \ \ \ \ (2)$

which contradicts the hypothesis that ${X|\Omega}$ is not stochastically totally bounded. Indeed, if (2) failed, then there must exist some local element ${x \in \Gamma(X|\Omega')}$ of ${X|\Omega}$ which does not lie in ${\Gamma(\bigcup_{n=1}^{\sup S} B(x_n,\epsilon)|\Omega')}$ . In particular, there must exist an event ${\Omega'' \subset \Omega'}$ of positive probability such that ${d(x,x_n) \geq \epsilon}$ on ${\Omega''}$ for all ${n \in {\bf N}_+|\Omega''}$ with ${n \leq \sup S|\Omega''}$ . If we then define ${x_{\sup S + 1}}$ on ${\Omega''}$ by ${x_{\sup S + 1} := x|\Omega''}$ , then we see that ${n \mapsto x_n}$ on ${\{ n \in {\bf N}_+: n \leq \sup S+1\}|\Omega''}$ is ${\epsilon}$ -separated on ${\Omega''}$ , and on gluing with the original ${n \mapsto x_n}$ on the complement of ${\Omega''}$ , we see that ${\sup_S + 1_{\Omega''}}$ lies in ${S}$ , contradicting the maximal nature of ${\sup_S}$ . Thus ${\sup S}$ is stochastically infinite with positive probability.

We may now pass to an event ${\Omega'}$ of positive probability on which ${\sup S = +\infty}$ . By definition of the supremum, we conclude that for every deterministic natural number ${N}$ , we may find a sequence ${x_{N,1},\dots,x_{N,N} \in \Gamma(X|\Omega')}$ which are ${\epsilon}$ -separated. Observe that if ${n < N}$ is a deterministic natural number and we have elements ${y_1,\dots,y_n \in \Gamma(X|\Omega')}$ , then we can find a stochastic ${m \leq N}$ on ${\Omega'}$ such that ${d(x_{N,m}, y_i) \geq \epsilon/2}$ for all ${i=1,\dots,N}$ , since each ${x_{N,m}}$ can stochastically lie within ${\epsilon/2}$ of at most one ${y_i}$ . (To see this rigorously, one can consider the Boolean geometry of the events on which ${d(x_{N,n},y_i) \geq \epsilon/2}$ stochastically hold for various ${n,i}$ .) By iterating this construction (and applying the axiom of countable choice externally), we may find an infinite sequence ${y_1,y_2,\dots}$ in ${\Gamma(X|\Omega')}$ which is ${\epsilon/2}$ -separated, but then this sequence cannot have a convergent subsequence, and so (ii) fails.

Now suppose that ${X|\Omega}$ is stochastically complete and stochastically totally bounded, and let ${(x_n)_{n \in {\bf N}_+}}$ be a sequence of local elements ${x_n \in \Gamma(X|\Omega')}$ of ${X|\Omega}$ for some event ${\Omega'}$ , which we may assume without loss of generality to have positive probability. By stochastic completeness, it suffices to find a stochastic subsequence ${(x_{n_j})_{j \in {\bf N}_+}}$ which is stochastically Cauchy on ${\Omega'}$ .

By stochastic total boundedness, one can find a stochastic natural number ${M_1 \in {\bf N}|\Omega'}$ and a stochastic map ${m \mapsto y_{1,m}}$ from ${\{ m \in {\bf N}_+: m \leq M_1\}|\Omega'}$ to ${X|\Omega'}$ , such that

$\displaystyle X|\Omega' = \bigcup_{m=1}^{M_1} B(y_{1,m},M_1)|\Omega'. \ \ \ \ \ (3)$

For each deterministic positive natural numbers ${m, n \in {\bf N}_+}$ , we define ${E_{m,n}}$ to be the event in ${\Omega'}$ that the assertions ${m \leq M_1}$ and ${d(x_n,y_{1,m})}$ both hold stochastically; this event is determined up to null events. From (3), we see that

$\displaystyle \bigcup_{m=1}^{M_1} E_{n,m} = \Omega'$

holds up to null events for all ${n \in {\bf N}_+}$ . In particular, we have

$\displaystyle \sum_{m=1}^{M_1} 1_{E_{n,m}} \geq 1$

almost surely on ${\Omega'}$ for all ${n \in {\bf N}_+}$ , and so on summing in ${n}$

$\displaystyle \sum_{m=1}^{M_1} \sum_{n \in {\bf N}_+} 1_{E_{n,m}} = +\infty$

almost surely on ${\Omega'}$ . By selecting ${m \in {\bf N}_+|\Omega'}$ stochastically to be the least ${m}$ for which ${\sum_{n \in {\bf N}_+} 1_{E_{n,m}}}$ is infinite, we have ${m \leq M_1}$ and

$\displaystyle \sum_{n \in {\bf N}_+} 1_{E_{n,m}} = +\infty$

almost surely on ${\Omega'}$ . We can then stochastically choose a sequence ${j_{1,1} < j_{1,2} < \dots}$ in ${{\bf N}_+|\Omega'}$ such that ${E_{n_{j_{1,i}},m}}$ holds almost surely on ${\Omega'}$ for each ${i \in {\bf N}_+}$ , or equivalently that the stochastic subsequence ${(x_{n_{j_{1,i}}})_{i \in {\bf N}_+}}$ lies in ${\Gamma( B(y_{1,m},1) | \Omega' )}$ . Writing ${z_1 := y_{1,m}}$ , we have thus localised this stochastic subsequence to a stochastic unit ball ${B(z_1,1)}$ .

By repeating this argument, we may find a further stochastic subsequence ${(x_{n_{j_{2,i}}})_{i \in {\bf N}_+}}$ of ${(x_{n_{j_{1,i}}})_{i \in {\bf N}_+}}$ that lies in ${\Gamma( B(z_2,1/2 )|\Omega')}$ for some ${z_2 \in \Gamma( X|\Omega')}$ , a yet further subsequence ${(x_{n_{j_{3,i}}})_{i \in {\bf N}_+}}$ that lies in ${\Gamma( B( z_3, 1/3)|\Omega' )}$ for some ${z_3 \in \Gamma(X|\Omega')}$ , and so forth. It is then easy to see that the diagonal sequence ${(x_{n_{j_{i,i}}})_{i \in {\bf N}_+}}$ is stochastically Cauchy, and the claim follows. $\Box$

For future reference, we remark that the above arguments also show that if ${Y|\Omega}$ is a stochastically totally bounded subset of a stochastically complete metric space ${X|\Omega}$ , then every sequence in ${\Gamma(Y|\Omega)}$ has a stochastic susbequence which converges in ${\Gamma(X|\Omega)}$ .

— 2. Hilbert-Schmidt operators relative to a finite measure space —

One could continue developing stochastic versions of other fundamental results in real analysis (for instance, working out the basic theory of stochastic continuous functions between metric spaces); roughly speaking, it appears that most of these results will go through as long as one does not require the concept of an uncountable union or intersection or the axiom of choice (in particular, I do not see how to develop a stochastic theory of arbitrary topological spaces, although the first countable case may be doable; also, any result reliant on the Hahn-Banach theorem or the non-sequential version of Tychonoff’s theorem will likely not have a good stochastic analogue). I will however focus on the results leading up to the stochastic version of the spectral theorem for Hilbert-Schmidt operators, as this is the application that motivated my post.

Let us first define the concept of a stochastic (real) Hilbert space, in more or less complete analogy with the deterministic counterpart:

Definition 10 (Stochastic Hilbert spaces) A stochastic vector space is a stochastic set ${V|\Omega}$ equipped with an element ${0 \in \Gamma(V|\Omega)}$ , an addition map ${+: V|\Omega \times V|\Omega \rightarrow V|\Omega}$ , and a scalar multiplication map ${\cdot: {\bf R}|\Omega \times V|\Omega \rightarrow V|\Omega}$ which obeys the usual vector space axioms. In other words, when localising to any event ${E}$ , the addition map ${+: \Gamma(V|E) \times \Gamma(V|E) \rightarrow \Gamma(V|E)}$ is commutative and associative with identity ${0|E}$ , and the scalar multiplication map ${\cdot: \Gamma({\bf R}|E) \times \Gamma(V|E) \rightarrow \Gamma(V|E)}$ is bilinear over ${\Gamma({\bf R}|\mathop{\bf E})}$ . In other words, ${\Gamma(V|E)}$ is a module over the commutative ring ${\Gamma({\bf R}|E)}$ . As is usual, we define the subtraction map ${-: V|\Omega \times V|\Omega \rightarrow V|\Omega}$ by the formula ${v-w := v + (-1) \cdot w}$ .

A stochastic inner product space is a stochastic vector space ${V|\Omega}$ equipped with an inner product map ${\langle,\rangle: V|\Omega \times V|\Omega \rightarrow {\bf R}|\Omega}$ which obeys the following axioms for any event ${E}$ :

(Symmetry) The map ${\langle,\rangle: \Gamma(V|E) \times \Gamma(V|E) \rightarrow \Gamma({\bf R}|E)}$ is symmetric.

(Bilinearity) The map ${\langle,\rangle: \Gamma(V|E) \times \Gamma(V|E) \rightarrow \Gamma({\bf R}|E)}$ is bilinear over ${\Gamma({\bf R}|E)}$ .

(Positive semi-definiteness) For any ${v \in\Gamma(V|E)}$ , we have ${\langle v,v \rangle \geq 0}$ , with equality if and only if ${v=0}$ .

By repeating the usual deterministic arguments, it is easy to see that any stochastic inner product space becomes a stochastic metric space with ${d(v,w) := \|v-w\|}$ , where ${\|v\| := \langle v,v \rangle^{1/2}}$ .

A stochastic Hilbert space is a stochastic inner product space ${H}$ which is also stochastically complete. We denote the inner product on such spaces by ${\langle,\rangle_H}$ and the norm by ${\| \|_H}$ .

As usual, in the model case when ${\Omega}$ is discrete and at most countable, a stochastic Hilbert space ${H|\Omega}$ is just a bundle of deterministic Hilbert spaces ${H_\omega}$ for each ${\omega \in \Omega}$ occurring with positive probability, with no relationships between the different fibres ${H_\omega}$ (in particular, their dimensions may vary arbitrarily in ${\omega}$ ). In the continuous case, the notion of a stochastic Hilbert space ${H|\Omega}$ is very closely related to that of (an extended version of) a Hilbert module over the commutative Banach algebra ${L^\infty(\Omega)}$ ; indeed, it is easy to see that the space of global elements ${v \in \Gamma(H|\Omega)}$ of a stochastic Hilbert space ${H|\Omega}$ which are bounded in the sense that ${\|v\| \leq M}$ for some deterministic real ${M}$ forms a Hilbert module over ${L^\infty(\Omega)}$ . (Without the boundedness restriction, one obtains instead a module over ${\Gamma({\bf R}|\Omega)}$ .)

Note that we do not impose any separability hypothesis on our Hilbert spaces. Despite this, much of the theory of Hilbert spaces turns out to still be of “countable complexity” in some sense, so that it can be extended to the stochastic setting without too much difficulty.

We now extend the familiar notion of an orthonormal system in a Hilbert space to the stochastic setting. A key point is that we allow the number of elements in this system to also be stochastic.

Definition 11 (Orthonormal system) Let ${H|\Omega}$ be a stochastic Hilbert space. A stochastic orthonormal system ${(e_n)_{n=1}^N|\Omega}$ in ${H|\Omega}$ consists of a stochastic extended natural number ${N \in {\bf N} \cup \{+\infty\}|\Omega}$ , together with a stochastic map ${n \mapsto e_n}$ from ${\{ n \in {\bf N}_+: n \leq N \}|\Omega}$ to ${H|\Omega}$ , such that one has ${\langle e_n, e_m \rangle = 1_{n=m}}$ on ${E}$ for any event ${E}$ and any ${n, m \in {\bf N}_+|E}$ with ${n,m \leq N|E}$ . (Note that we allow ${N}$ to vanish with positive probability, so that the orthonormal system can be stochastically empty.)

Now we can define the notion of a stochastic Hilbert-Schmidt operator.

Definition 12 (Stochastic Hilbert-Schmidt operator) Let ${H|\Omega}$ and ${H'|\Omega}$ be stochastic Hilbert spaces. A stochastic linear operator ${T: H|\Omega \rightarrow H'|\Omega}$ is a stochastic function such that for each event ${E}$ , the localised maps ${T: \Gamma(H|E) \rightarrow \Gamma(H'|E)}$ are linear over ${\Gamma({\bf R}|E)}$ . Such an operator is said to be stochastically bounded if there exists a non-negative stochastic real ${A \in \Gamma([0,+\infty)|\Omega)}$ such that one has

$\displaystyle \| Tv \|_{H'} \leq A|E$

for all events ${E}$ and local elements ${v \in \Gamma(H|E)}$ . By (the negation of) Theorem 5, there is a least such ${A}$ , which we denote as ${\|T\|_{B(H \rightarrow H')} \in \Gamma([0,+\infty)|\Omega)}$ .

Similarly, we say that a stochastic linear operator ${T: H|\Omega \rightarrow H'|\Omega}$ is stochastically Hilbert-Schmidt if there exists a non-negative stochastic real ${A \in \Gamma([0,+\infty)|\Omega)}$ such that one has

$\displaystyle \sum_{n=1}^N \sum_{m=1}^M |\langle T e_n, f_m \rangle|^2 \leq A^2|E$

for all events ${E}$ and all stochastic orthonormal systems ${(e_n)_{n=1}^N|E, (f_m)_{m=1}^M|E}$ on ${H|E}$ and ${H'|E}$ respectively. Again, there is a least such ${A}$ , which we denote as ${\|T\|_{HS(H \rightarrow H')} \in \Gamma([0,+\infty)|\Omega)}$ .

A stochastic linear operator ${T: H|\Omega \rightarrow H'|\Omega}$ is said to be compact if the image ${T( \{ v \in H: \|v\| \leq 1 \} )|\Omega}$ of the unit ball ${\{v \in H: \|v\| \leq 1\}|\Omega}$ is stochastically totally bounded in ${H'|\Omega}$ .

Exercise 8 Show that any stochastic Hilbert-Schmidt operator ${T: H|\Omega \rightarrow H'|\Omega}$ obeys the bound

$\displaystyle \sum_{n=1}^N \| T e_n \|_{H'}^2 \leq \|T\|_{HS(H \rightarrow H')}^2|E$

for all events ${E}$ and all stochastic orthonormal systems ${(e_n)_{n=1}^N|E}$ on ${H|E}$ . Conclude in particular that ${T}$ is stochastically bounded with ${\|T\|_{B(H \rightarrow H')} \leq \|T\|_{HS(H \rightarrow H')}}$ .

We have the following basic fact:

Proposition 13 Any stochastic Hilbert-Schmidt operator ${T: H|\Omega \rightarrow H'|\Omega}$ is stochastically compact.

Proof: Suppose for contradiction that we could find a stochastic Hilbert-Schmidt operator ${T: H|\Omega \rightarrow H'|\Omega}$ which is not stochastically compact, thus ${T( \{ v \in H: \|v\| \leq 1 \} )|\Omega}$ is not stochastically totally bounded. By repeating the arguments used in the proof of Theorem 9, this means that there exists an event ${\Omega'}$ of positive probability, a stochastic real ${\epsilon > 0}$ on ${\Omega'}$ , and an infinite sequence ${x_n \in \Gamma(\{ v \in H: \|v\| \leq 1 \}|\Omega')}$ for ${n\in {\bf N}_+}$ such that the ${Tx_n}$ are ${\epsilon}$ -separated on ${\Omega'}$ .

We will need a stronger separation property. Let us say that a sequence ${y_m \in \Gamma(H'|\Omega')}$ is linearly ${\epsilon/4}$ -separated if one has

$\displaystyle \| y_m - c_1 y_1 - \dots - c_{m-1} y_{m-1} \|_{H'} \geq \epsilon/4 \ \ \ \ \ (4)$

on ${\Omega'}$ for any deterministic ${m \in{\bf N}_+}$ and any stochastic reals ${c_1,\dots,c_{m-1} \in {\bf R}|\Omega'}$ . We claim that ${\Gamma(T(\{ v \in H: \|v\| \leq 1 \})|\Omega')}$ contains an infinite sequence ${y_m}$ that is linearly ${\epsilon/4}$ -separated. Indeed, suppose that we have already found a finite sequence ${y_1,\dots,y_{m-1}}$ in ${\Gamma(T(\{ v \in H: \|v\| \leq 1 \})|\Omega')}$ that is linearly ${\epsilon/4}$ -separated for some ${m \geq 1}$ , and wish to add on a further element ${y_m}$ while preserving the linear ${\epsilon}$ -separation property, that is to say we wish to have (4) for all ${c_1,\dots,c_{m-1} \in {\bf R}|\Omega'}$ . By Exercise 8, such a ${y_m}$ would already lie in the closed ball ${B( 0, \|T\|_{HS(H \rightarrow H')})}$ . Now, by elementary geometry (applying a Gram-Schmidt process to the ${y_1,\dots,y_{m-1}}$ ) one can cover the stochastic set

$\displaystyle \{ y \in H': \|y\| \leq \|T\|_{HS(H \rightarrow H')}; \| y - c_1 y_1 - \dots - c_{m-1} y_{m-1} \|_{H'} < \epsilon/4 \hbox{ for some } c_1,\dots,c_{m-1} \in {\bf R} \}|\Omega'$

by a finite union of balls

$\displaystyle \bigcup_{i=1}^N B( z_i, \epsilon/2 )$

for some stochastic ${N \in {\bf N}|\Omega'}$ and some stochastic finite sequence ${(z_i)_{i=1}^N|\Omega'}$ of points in ${H'|\Omega'}$ . Stochastically, each of these balls ${B(z_i,\epsilon/2)}$ may contain at most one of the ${x_n}$ ; if we then define the stochastic positive natural number ${n \in {\bf N}_+|\Omega'}$ to be the least ${x_n}$ that stochastically lies outside all of the ${B(z_i,\epsilon/2)}$ , then ${n}$ is well-defined, and if we set ${y_m := x_n}$ , we obtain the desired property (4).

As each ${y_m}$ lies in ${\Gamma(T(\{ v \in H: \|v\| \leq 1 \})|\Omega')}$ , we have ${y_m = T v_m}$ for some ${v_m \in \Gamma(H|\Omega')}$ with ${\|v_m\|_H \leq 1}$ . From the Gram-Schmidt process, one may find an orthonormal system ${(e_n)_{n=1}^N|\Omega'}$ in ${\Gamma(H|\Omega')}$ for some ${N \in {\bf N} \cup\{+\infty\}|\Omega'}$ such that each ${v_m}$ is a linear combination (over ${\Gamma({\bf R}|\Omega')}$ ) of those ${e_n}$ with ${n \leq N, m}$ . We may similarly find an orthonormal system ${(f_m)_{m=1}^M|\Omega'}$ in ${\Gamma(H'|\Omega')}$ for some ${N \in {\bf N} \cup\{+\infty\}|\Omega'}$ such that each ${y_m}$ is a linear combination of those ${f_i}$ with ${i \leq M,m}$ . From (4) we conclude that ${M=+\infty}$ and that for each deterministic ${m \in {\bf N}_+}$ , the ${f_m}$ coefficient of ${y_m}$ has magnitude at least ${\epsilon/4}$ , thus

$\displaystyle |\langle T x_m, f_m \rangle| \geq \epsilon/4$

and thus by the Pythagoras theorem

$\displaystyle \sum_{n=1}^N |\langle T e_n, f_m \rangle|^2 \geq \epsilon^2/16$

on ${\Omega'}$ ; summing in ${m}$ , we contradict the Hilbert-Schmidt nature of ${T}$ . $\Box$

Next, we establish the existence of adjoints:

Theorem 14 (Adjoint operator) Let ${T: H|\Omega \rightarrow H'|\Omega}$ be a stochastically bounded linear operator. Then there exists a unique stochastically bounded linear operator ${T^*: H'|\Omega \rightarrow H|\Omega}$ such that

$\displaystyle \langle Tv, w \rangle_{H'} = \langle v, T^* w \rangle_H$

on any event ${E}$ and any ${v \in \Gamma(H|E)}$ , ${w \in \Gamma(H'|E)}$ . In particular we have ${\|T\|_{B(H \rightarrow H')} = \|T^*\|_{B(H' \rightarrow H)}}$ .

Proof: Uniqueness is an easy exercise that we leave to the reader, so we focus on existence. The point here is that the Riesz representation theorem for Hilbert spaces is sufficiently “constructive” that it can be translated to the stochastic setting.

Let ${E}$ be an event and ${w \in \Gamma(H'|E)}$ be a local element of ${H'}$ . We let ${S}$ be the stochastic set on ${E}$ defined by setting ${\Gamma(S|F)}$ for ${F \subset E}$ to be the set of all stochastic real numbers of the form ${\langle T v, w \rangle_{H'}}$ , where ${v \in \Gamma(H|F)}$ with ${\|v\|_H \leq 1}$ . By Theorem 5, we may then find a sequence ${v_n \in \Gamma(H|E)}$ for ${n \in {\bf N}_+}$ such that ${\langle T v_n, w \rangle_{H'}}$ converges stochastically to ${\sup S}$ on ${E}$ . For any two ${n,m \in{\bf N}_+}$ , we have from the parallelogram law that

$\displaystyle \| \frac{v_n+v_m}{2} \|_H \leq (1 - \frac{1}{2} \|v_n-v_m\|_H^2)^{1/2}$

and hence by homogeneity

$\displaystyle \frac{1}{2} ( \langle T v_n, w \rangle_H + \langle T v_m, w \rangle_H ) \leq (1 - \frac{1}{2} \|v_n-v_m\|_H^2)^{1/2} \sup S$

on ${E}$ combining this with the stochastic convergence of ${\langle T v_n, w \rangle_{H'}}$ , we conclude that ${v_n}$ is stochastically Cauchy on the event in ${E}$ that ${\sup S}$ is non-zero. Setting ${v_\infty \in \Gamma(H|E)}$ to be the stochastic limit of the ${v_n}$ on this event (and set to ${0}$ on the complementary event), we see that ${\|v_\infty\|_H \leq 1}$ and

$\displaystyle \langle Tv_\infty, w \rangle_{H'} = \sup S.$

On the event that ${\sup S}$ is non-zero, ${v_\infty}$ is thus non-zero, and consideration of the vectors ${v_\infty + tu}$ for stochastic real ${t}$ and stochastic vectors ${u}$ soon reveals that

$\displaystyle \langle Tu, w \rangle_{H'} = 0$

whenever ${\langle u, v_\infty \rangle_H = 0}$ , which by elementary linear algebra gives a representation of the form

$\displaystyle \langle Tv, w \rangle_{H'} = \langle v, T^* w \rangle_{H}$

for some ${T^* w}$ (a scalar multiple of ${v_\infty}$ ); when ${\sup S}$ vanishes, we simply take ${T^* w=0}$ . It is then a routine matter to verify that ${T^*}$ is a stochastically bounded linear operator, and the claim follows. $\Box$

We use this to relativise the spectral theorem (or more precisely, the singular value decomposition) for compact operators:

Theorem 15 (Spectral theorem for stochastically compact operators) Let ${T: H|\Omega \rightarrow H'|\Omega}$ be a stochastically compact linear operator, with ${T^*}$ also stochastically compact. Then there exists ${N \in \Gamma({\bf N} \cup \{+\infty\}|\Omega)}$ , orthonormal systems ${(e_n)_{n=1}^N|\Omega}$ and ${(f_n)_{n=1}^N|\Omega}$ of ${H|\Omega}$ and ${H'|\Omega}$ respectively, and a stochastic sequence ${(\sigma_n)_{n=1}^N|\Omega}$ in ${(0,+\infty)|\Omega}$ such that ${\sigma_n \geq \sigma_m}$ on an event ${E}$ whenever ${1 \leq m \leq n \leq N}$ are stochastic natural numbers on ${E}$ , and such that the ${\sigma_n}$ go to zero in the sense that for any stochastic real ${\epsilon>0}$ on an event ${E}$ , there exist a stochastic natural number ${N_\epsilon}$ on ${E}$ such that ${\sigma_n \leq \epsilon}$ on ${E}$ whenever ${N_\epsilon \leq n \leq N}$ is a stochastic natural number on ${E}$ . Furthermore, for any event ${E}$ and ${v \in \Gamma(H|E)}$ , one has

$\displaystyle Tv = \sum_{n=1}^N \sigma_n \langle v, e_n \rangle_H f_n$

on ${E}$ . (Note that a Bessel inequality argument shows that the series is convergent; indeed it is even unconditionally convergent.)

It is likely that the hypothesis that ${T^*}$ be stochastically compact is redundant, in that it is implied by the stochastically compact nature of ${T}$ , but I did not attempt to prove this rigorously as it was not needed for my application (which is focused on the Hilbert-Schmidt case).

To prove this theorem, we first establish a fragment of it for the top singular value ${n=1}$ :

Theorem 16 (Largest singular value) Let ${T: H|\Omega \rightarrow H'|\Omega}$ be a stochastically compact linear operator, and let ${\Omega'}$ be the event where ${\|T\|_{B(H \rightarrow H')} > 0}$ (this event is well-defined up to a null event). Then there exist ${e \in \Gamma(H|\Omega')}$ , ${f \in \Gamma(H'|\Omega')}$ with ${\|e\|_H = \|f\|_{H'} = 1}$ on ${\Omega'}$ , such that

$\displaystyle Te = \|T\|_{B(H \rightarrow H')} f$

and dually that

$\displaystyle T^* f = \|T\|_{B(H \rightarrow H')} e$

on ${\Omega'}$ .

Proof: Note that ${H,H'}$ are necessarily non-trivial on ${\Omega'}$ . Let ${S}$ denote the set of all expressions of the form ${\langle Te, f\rangle}$ on ${\Omega'}$ , where ${e \in \Gamma(H|\Omega')}$ , ${f \in \Gamma(H'|\Omega')}$ with ${\|e\|_H = \|f\|_{H'} = 1}$ on ${\Omega'}$ , then ${S}$ is a globally non-empty stochastic subset of ${[0,+\infty)|\Omega'}$ which has ${\|T\|_{op}}$ as an upper bound. Indeed, from Theorem 5 and the definition of ${\|T\|_{B(H \rightarrow H')}}$ , it is not hard to see that ${\|T\|_{B(H \rightarrow H')} = \sup S}$ . From this, we may construct a sequence in ${S}$ that converges stochastically to ${\|T\|_{B(H \rightarrow H')}}$ on ${\Omega'}$ , and hence we may find sequences ${e_n \in \Gamma(H|\Omega')}$ , ${f_n \in \Gamma(H'|\Omega')}$ for ${n \in{\bf N}}$ with ${\|e_n\|_H = \|f_n\|_{H'} = 1}$ on ${\Omega'}$ with ${\langle Te_n, f_n\rangle}$ stochastically convergent to ${\|T\|_{B(H \rightarrow H')}}$ . By the Cauchy-Schwarz inequality, this implies that ${\|Te_n\|_{H'}}$ is stochastically convergent to ${\|T\|_{B(H \rightarrow H')}}$ ; from the parallelogram law applied to ${f_n}$ and ${Te_n / \|T\|_{B(H \rightarrow H')}}$ , we conclude that ${f_n - Te_n / \|T\|_{B(H \rightarrow H')}}$ converges stochastically to zero. On the other hand, as ${T}$ is compact, we can pass to a stochastic subsequence and ensure that ${Te_n}$ is stochastically convergent, thus ${f_n}$ is also stochastically convergent to some limit ${f \in \Gamma(H'|\Omega)}$ . Similar considerations using the adjoint operator ${T^*}$ allow us to assume that ${e_n}$ is stochastically convergent to some limit ${e \in \Gamma(H|\Omega)}$ . It is then routine to verify that ${\|e\|_H = \|f\|_{H'} = 1}$ , ${f - Te / \|T\|_{B(H \rightarrow H')} = 0}$ , and ${e - T^* e / \|T\|_{B(H \rightarrow H')} = 0}$ , giving the claim. $\Box$

Now we prove Theorem 15.

Proof: (Proof of Theorem 15.) Define a partial singular value decomposition to consist of the following data:

A stochastic extended natural number ${N \in \Gamma({\bf N} \cup \{+\infty\}|\Omega)}$ ;
A stochastic orthonormal system ${(e_n)_{n=1}^N|\Omega}$ of ${H|\Omega}$ ;
A stochastic orthonormal system ${(f_n)_{n=1}^N|\Omega}$ of ${H'|\Omega}$ ; and
A non-increasing stochastic sequence ${(\sigma_n)_{n=1}^N|\Omega}$ in ${(0,+\infty)|\Omega}$

such that, for any event ${E}$ , and any ${n \in {\bf N}_+|E}$ with ${n \leq N|E}$ ,

${Te_n = \sigma_n f_n}$ on ${E}$ .
${T^* f_n = \sigma_n e_n}$ on ${E}$ .
Whenever ${v \in H|E}$ is orthogonal to ${e_m}$ for all ${m \leq n}$ , one has ${\|T v \|_{H'} \leq \sigma_n \|v\|_H}$ on ${E}$ .
Whenever ${n \in {\bf N}_+|E}$ with ${n \leq N|E}$ and ${w \in H'|E}$ is orthogonal to ${f_m}$ for all ${m \leq n}$ , one has ${\|T^* w \|_{H} \leq \sigma_n \|v\|_{H'}}$ on ${E}$ .

We let ${S}$ be the set of all ${N}$ that can arise from a partial singular value decomposition; then ${S}$ is a stochastic subset of ${{\bf N} \cup \{\infty\}|\Omega}$ that contains ${0|\Omega}$ , and by Theorem 5 we can form the supremum ${\sup S \in {\bf N} \cup \{\infty\}|\Omega}$ .

Let us first localise to the event ${\Omega'}$ that ${\sup S}$ is stochastically finite. As in the proof of the Heine-Borel theorem, we can use the discrete nature of the natural numbers to conclude that ${\sup S \in S}$ on ${\Omega'}$ . Thus there exists a partial singular value decomposition on ${\Omega'}$ with ${N=\sup S}$ .

Define ${\tilde H}$ on ${\Omega'}$ by setting ${\Gamma(\tilde H|E)}$ for ${E \subset \Omega'}$ to be the set of all ${v \in \Gamma(H|E)}$ that are orthogonal to all the ${e_n}$ with ${n \leq N}$ ; this can easily be seen to be a stochastic Hilbert space (a stochastically finite codimension subspace of ${H}$ ). Similarly define ${\tilde H'}$ on ${\Omega'}$ by setting ${\Gamma(\tilde H'|E)}$ to be the set of all ${w \in \Gamma(H'|E)}$ that are orthogonal to all the ${f_n}$ with ${n \leq N}$ . As ${Te_n = \sigma_n f_n}$ and ${T^* f_n = \sigma_n e_n}$ , we see that ${T}$ maps ${\tilde H}$ to ${\tilde H'}$ , and ${T^*}$ maps ${\tilde H'}$ to ${\tilde H}$ ; from the remaining axioms of a partial singular value decomposition we see that ${\|T\|_{B(\tilde H \rightarrow \tilde H')}}$ on ${\Omega'}$ . If ${\|T\|_{B(\tilde H \rightarrow \tilde H')}}$ vanishes, then ${T}$ vanishes on ${\tilde H}$ , and one easily obtains the required singular value decomposition in ${\Omega'}$ . Now suppose for contradiction that ${\|T\|_{B(\tilde H \rightarrow \tilde H')}}$ does not (deterministically) vanish, so there is a subevent ${E}$ of ${\Omega'}$ of positive probability on which ${\|T\|_{B(\tilde H \rightarrow \tilde H')}}$ is positive. By Theorem 16, we can then find unit vectors ${e_{N+1} \in \Gamma(\tilde H|E)}$ and ${f_{N+1} \in \Gamma(\tilde H'|E)}$ such that

$\displaystyle Te_{N+1} = \|T\|_{B(\tilde H \rightarrow \tilde H')} f_{N+1}$

and

$\displaystyle T^* f_{N+1} = \|T\|_{B(\tilde H \rightarrow \tilde H')} e_{N+1}.$

If we then set ${\sigma_{N+1} := \|T\|_{B(\tilde H \rightarrow \tilde H')}}$ , we can obtain a partial singular value decomposition on ${E}$ with ${N}$ now set to ${\sup S+1}$ ; gluing this with the original partial singular value of decomposition on the complement of ${E}$ , we contradict the maximality of ${S}$ . This concludes the proof of the spectral theorem on the event that ${\sup S < \infty}$ .

Now we localise to the complementary event ${\Omega''}$ that ${\sup S}$ is infinite. Now we need to run a compactness argument before we can ensure that ${\sup S}$ actually lies in ${S}$ . Namely, for any deterministic natural number ${M}$ , we can find a partial singular value decomposition with data ${N_M, (e_{M,n})_{n=1}^{N_M}, (f_{M,n})_{n=1}^{N_M}, (\sigma_{M,n})_{n=1}^{N_M}}$ on ${\Omega''}$ such that ${N_M \geq M}$ . We now claim that the ${\sigma_{M,n}}$ decay in ${n}$ uniformly in ${M}$ in the following sense: for any deterministic real ${\epsilon > 0}$ , there exists a stochastic ${L_\epsilon \in \Gamma({\bf N}|\Omega'')}$ such that ${\sigma_{M,n} \leq \epsilon}$ whenever ${m \in {\bf N}}$ and ${n \in \Gamma({\bf N}|\Omega'')}$ are such that ${L_\epsilon < n \leq N_M}$ . Indeed, from the total boundedness of ${T \{ v \in H: \|v\|_H \leq 1\}|\Omega''}$ , one can cover this space by a union ${\bigcup_{i=1}^{L_\epsilon} B(w_i, \epsilon/2)}$ of balls of radius ${\epsilon/2}$ for some ${L_\epsilon \in \Gamma({\bf N}|\Omega'')}$ . If ${L_\epsilon < n \leq N_M}$ is such that ${\sigma_{M,n} > \epsilon}$ on some event ${E \subset \Omega''}$ of positive probability, then the vectors ${T e_{M,m} = \sigma_{M,m} f_{M,m}}$ for ${m \leq n}$ are ${\epsilon}$ -separated on ${E}$ by Pythagoras’s theorem, leading to a contradiction since each ball ${B(w_i,\epsilon/2)}$ can capture at most one of these vectors. This gives the claim.

By repeatedly passing to stochastic subsequences and diagonalising, we may assume that ${\sigma_{M,n}}$ converges stochastically to a limit ${\sigma_n \in [0,+\infty)}$ as ${M \rightarrow \infty}$ for each ${n \in {\bf N}}$ which is non-increasing. By compactness of ${T}$ , we may also assume that the ${T e_{M,m} = \sigma_{M,m} f_{M,m}}$ are stochastically convergent in ${M}$ for each fixed ${m}$ , which implies that the ${f_{M,m}}$ converge stochastically to a limit ${f_m}$ whenever ${\sigma_m > 0}$ . A similar argument using the compactness of ${T^*}$ allows us to assume that ${e_{M,m}}$ converges stochastically to a limit ${e_m}$ whenever ${\sigma_m > 0}$ . One then easily verifies that the ${e_m}$ and ${f_m}$ are orthonormal systems when restricted to those ${m}$ for which ${\sigma_m> 0}$ . Furthermore, a limiting argument shows that whenever ${\epsilon>0}$ is a deterministic real, ${E \subset \Omega''}$ is an event, and ${v \in \Gamma(H|E)}$ is a unit vector orthogonal to ${e_m}$ for those ${m \leq L_\epsilon}$ with ${\sigma_m > 0}$ , then ${\|Tv\|_H \leq \epsilon}$ . From this and a decomposition into orthonormal bases and a limiting argument we see that

$\displaystyle Tv = \sum_{1 \leq n \leq N; \sigma_n > 0} \sigma_n \langle v, e_n \rangle_H f_n$

on ${E}$ for any ${v \in \Gamma(H|E)}$ , and the claim follows. $\Box$

Finally, we specialise to the example of Hilbert modules from Example 3.

Corollary 17 (Singular value decomposition on Hilbert modules) Let ${\Omega_1, \Omega_2}$ be extensions of a finite measure space ${\Omega}$ , with factor maps ${\pi_1: \Omega_1 \rightarrow \Omega}$ and ${\pi_2: \Omega_2 \rightarrow \Omega}$ . Let ${T: L^2(\Omega_1) \rightarrow L^2(\Omega_2)}$ be a bounded linear map (in the ${L^2}$ sense) which is also linear over ${L^\infty(\Omega)}$ (which embeds via pullback into ${L^\infty(\Omega_1)}$ and ${L^\infty(\Omega_2)}$ ); note that ${T}$ may be extended to a linear map from ${L^2(\Omega_1|\Omega)}$ to ${L^2(\Omega_2|\Omega)}$ . Assume the following Hilbert-Schmidt property: there exists a measurable ${A: \Omega \rightarrow [0,+\infty)}$ such that

$\displaystyle \sum_{m=1}^M \sum_{n=1}^N |(\pi_2)_*( (T e_n) f_m )|^2 \leq A^2$

for all measurable ${M,N: \Omega \rightarrow {\bf N} \cup \{\infty\}}$ and all ${e_n \in L^2(\Omega_1), f_m \in L^2(\Omega_2)}$ that are orthonormal systems over ${L^\infty(\Omega_1)}$ in the sense that

$\displaystyle (\pi_1)_*(e_n e_{n'}) = 1_{n=n'}$

whenever ${n,n' \leq N}$ , and similarly

$\displaystyle (\pi_2)_*(f_m f_{m'}) = 1_{m=m'}$

whenever ${m,m' \leq M}$ . Then one can find a measurable ${N: \Omega \rightarrow {\bf N} \cup \{\infty\}}$ , orthonormal systems ${e_n, f_n \in L^2(\Omega_1)}$ , and ${\sigma_n: \Omega \rightarrow (0,+\infty)}$ defined for ${n \leq N}$ that are non-increasing and decay to zero as ${n \rightarrow \infty}$ (in the case ${N=+\infty}$ ), such that

$\displaystyle T g = \sum_{n=1}^N \sigma_n (\pi_1)_*(g e_n) f_n$

for all ${g \in L^2(\Omega_1)}$ .

In the case that ${\Omega}$ and ${\Omega'}$ are standard Borel, one can obtain this result from the classical spectral theorem via a disintegration argument. However, without such a standard Borel assumption, the most natural way to proceed appears to be through the above topos-theoretic machinery. This result can be used to establish some of the basic facts of the Furstenberg-Zimmer structure theory of measure-preserving systems, and specifically that weakly mixing functions relative to a given factor form the orthogonal complement to compact extensions of that factor, and that such compact extensions are the inverse limit of finite rank extensions. With the above formalism, this can be done even for measure spaces that are not standard Borel, and actions of groups that are not countable; I hope to discuss this in a subsequent post.

12 comments

Comments feed for this article

15 July, 2014 at 5:42 am

kawhi w

Oh, my. You get up so early if you are now in LA!

15 July, 2014 at 10:19 am

Babuji

What a brilliant synthesis. Mozart at work.

15 July, 2014 at 12:01 pm

Roger Purves

A trifling comment, but In the third paragraph, I would have expected you to start with a measure space, since a measure (or some sort of sigma-ideal appended to a measurable space) is required to get to the almost sure equalities.

(Thank you for the wonderful and generous blog.)

Roger Purves

15 July, 2014 at 12:08 pm

Terence Tao

To describe almost sure equivalence of two maps $f, f': \Omega \to X$ , the base $\Omega$ needs to be a measure space, but the range $X$ only needs to be a measurable space.

16 July, 2014 at 3:38 am

Roger Purves

Oops! I am feeling a little sheepish about reading so carelessly. Thank you for taking the time to spell it out.

16 July, 2014 at 2:27 pm

Miguel Lacruz

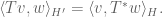
The display before Theorem 15 reads $\langle Tv,w \rangle_{H^\prime} = \langle v,T^\ast w \rangle_{H^\prime}$ and it should read $\langle Tv,w \rangle_{H^\prime} = \langle v,T^\ast w \rangle_{H}.$

[Corrected, thanks – T.]

17 July, 2014 at 6:01 am

MrCactu5 (@MonsieurCactus)

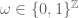I am thrown off. You are doing analysis with respect to “finite” measure spaces. How should I think of $\Omega$ ? Should I think of $\omega \in \{ 0,1 \}$ or $\omega \in \{ 0,1 \}^\mathbb{Z}$ ? What is finite here?

In any case, I think $\Omega$ the space of exogenous “stuff” we can’t account for.

17 July, 2014 at 9:56 pm

Terence Tao

A finite measure space is a measure space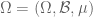 $\Omega = (\Omega, {\mathcal B}, \mu)$ whose total measure $\mu(\Omega)$ is finite; for instance, the unit interval $[0,1]$ with Lebesgue measure is a finite measure space, and more generally all probability spaces are finite measure spaces.

27 July, 2014 at 4:44 am

Hongseok Yang

Would you spell out the definitions of the stochastic sets ${\bf N} | \Omega$ and $\{true, false\} | \Omega$ ? Thanks.

[See Example 2. -T]

28 July, 2014 at 6:07 am

Dan Lacker

Really lovely post! And since I’m new here, I must thank you for maintaining a fantastic blog.

I want to point out a striking resemblance between much of this post and the theory of “conditional sets,” developed recently in this paper. (See also this PhD thesis for a more thorough account.)

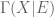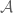To summarize: A conditional set is like a stochastic set, except that $\Gamma(X|E)$ may be indexed by elements $E$ of a fixed complete Boolean algebra $\mathcal{A}$ (satisfying an important additional assumption). A notable special case is when 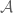$\mathcal{A}$ is the family of measurable subsets of some finite measure space, modulo null sets. 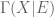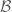In your definition of stochastic set, it seems natural to index $\Gamma(X|E)$ by $\mathcal{B}$ -modulo-null-sets, rather than by $\mathcal{B}$ itself, in which case a stochastic set would be a special case of conditional set. The above papers also work through some natural notions of analysis relative to conditional sets, parallel to the first part of this post (up to section 2), as well as general topological spaces. If you work modulo null sets, the measure algebra satisfies the countable chain condition, which appears to be essentially what allows the authors to make sense of uncountable unions of (and thus general topological spaces built on) conditional sets.

20 July, 2015 at 8:23 pm

A nonstandard analysis proof of Szemeredi’s theorem | What's new

[…] the relative spectral theorem for relative Hilbert-Schmidt operators (see Corollary 17 of this blog post), we may thus find relatively orthonormal systems in and respectively over and a non-increasing […]

17 March, 2024 at 12:31 pm

Anonymous

Professor Tao … I have deep feeling for the mathematical notions you discuss here but I do not have the particular mathematical linguistic fluency to participate in the accepted technical lexicon of your discussions. I am able to describe some mathematical objects in my own language and vocabulary which you would have to intuit and translate into your own parallel orthodox thought image.
I have a question regarding ‘deterministic’ objects and ‘stochastic’ objects. I follow many of your lectures such as Correlations of Multiplicative Functions, Erdos Discrepancy Problem, Pseudorandomness of the Liouville function and other end of the line discussion on the seive Parity problem. I work on the Parity problem … and have found some answers.

Do you consider a list of consecutive primes a deterministic object or a stochastic object? … do you consider the number of primes less than a number n,say Pi(n), to be a deterministically defined number or only approachable by randomness study?
In your public addresses you always preface that a synthesis of the distribution of the primes is the fundamental drive of Number theory, besides being your avowed personal quest/hobby … You have made many advances in understanding relationships between individual elements of the set of primes … have you ever considered the set of primes as a set with one element? … that element being the full, or some finite set, of the primes. In some sense such an outlook might suggest looking for relationships between individual anonymous primes is a bit meaningless and history suggests that it has never been all that fruitfull. Maybe all one has to do his figure out how to make ONE element. Maybe ALL the primes are made in one fell swoop. Such as maybe by applying one operation to the number 1 … division is the operation that comes to mind for me but many might say multiplication could be the trigger for a massive instantaneous avalanche of the infinite set of individual primes as the lone element of the set of primes. Inside this lone element lets stick to some cut off point n in the natural numbers ie make it finite. Then the number of elements inside this single element of the set of primes is Pi(n)

Now Pi(n) is precisely and exactly our number n, minus, the number of composite numbers less than n. More accurately it is (n-1) minus the number of composite numbers, call C(n) less/equal to n.
C(n) is absolutely 100% deterministically combinatorically computer countable from the list of primes up to n/2 … very simple beautiful algorithm extracted from non-repeating Eratothsenes seive-like multiplication procedure to count the composite numbers less than n. Pi(n) = (n-1)- C(n) is 100% direct simple exact countable function of Pi(n/2) … pure deterministic relationship between the two numbers at x and 2x. So what I’m saying here Professor Tao is: give me the list of primes up to x and I will give you the EXACT number of primes up to 2x … on a simple PC with no factorization of any numbers after x required … tested to n = 10^15 takes about ten hours

A simple equivalent output of the algorithm which incidentally carries ALL information on the Liouville function produces the sum of the Liouville function … my seive identifies the parity of every number less than n from only information on numbers less than n/2 … the secret is in the ordered harmonic structure of the algorithm
Jenda Vondra

	Anonymous on Infinite partial sumsets in th…
	Anonymous on A Banach algebra proof of the…
	Anonymous on A Banach algebra proof of the…
	Aleksandar on 245C, Notes 4: Sobolev sp…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Terence Tao on 245C, Notes 4: Sobolev sp…
	Terence Tao on 275A, Notes 3: The weak and st…
	Terence Tao on What is a gauge?
	Terence Tao on Erratum for “An inverse…
	Terence Tao on 275A, Notes 3: The weak and st…
	Terence Tao on An epsilon of room: pages from…
	Aleksandar on 245C, Notes 4: Sobolev sp…

Real analysis relative to a finite measure space

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

12 comments

Leave a comment Cancel reply

For commenters

Real analysis relative to a finite measure space

Share this:

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

12 comments

Leave a comment Cancel reply

For commenters