The 2014 Fields medallists have just been announced as (in alphabetical order of surname) Artur Avila, Manjul Bhargava, Martin Hairer, and Maryam Mirzakhani (see also these nice video profiles for the winners, which is a new initiative of the IMU and the Simons foundation). This time four years ago, I wrote a blog post discussing one result from each of the 2010 medallists; I thought I would try to repeat the exercise here, although the work of the medallists this time around is a little bit further away from my own direct area of expertise than last time, and so my discussion will unfortunately be a bit superficial (and possibly not completely accurate) in places. As before, I am picking these results based on my own idiosyncratic tastes, and they should not be viewed as necessarily being the “best” work of these medallists. (See also the press releases for Avila, Bhargava, Hairer, and Mirzakhani.)
Artur Avila works in dynamical systems and in the study of Schrödinger operators. The work of Avila that I am most familiar with is his solution with Svetlana Jitormiskaya of the ten martini problem of Kac, the solution to which (according to Barry Simon) he offered ten martinis for, hence the name. (The problem had also been previously posed in the work of Azbel and of Hofstadter.) The problem involves perhaps the simplest example of a Schrödinger operator with non-trivial spectral properties, namely the almost Mathieu operator defined for parameters
and
by a discrete one-dimensional Schrödinger operator with cosine potential:
This is a bounded self-adjoint operator and thus has a spectrum that is a compact subset of the real line; it arises in a number of physical contexts, most notably in the theory of the integer quantum Hall effect, though I will not discuss these applications here. Remarkably, the structure of this spectrum depends crucially on the Diophantine properties of the frequency
. For instance, if
is a rational number, then the operator is periodic with period
, and then basic (discrete) Floquet theory tells us that the spectrum is simply the union of
(possibly touching) intervals. But for irrational
(in which case the spectrum is independent of the phase
), the situation is much more fractal in nature, for instance in the critical case
the spectrum (as a function of
) gives rise to the Hofstadter butterfly. The “ten martini problem” asserts that for every irrational
and every choice of coupling constant
, the spectrum is homeomorphic to a Cantor set. Prior to the work of Avila and Jitormiskaya, there were a number of partial results on this problem, notably the result of Puig establishing Cantor spectrum for a full measure set of parameters
, as well as results requiring a perturbative hypothesis, such as
being very small or very large. The result was also already known for
being either very close to rational (i.e. a Liouville number) or very far from rational (a Diophantine number), although the analyses for these two cases failed to meet in the middle, leaving some cases untreated. The argument uses a wide variety of existing techniques, both perturbative and non-perturbative, to attack this problem, as well as an amusing argument by contradiction: they assume (in certain regimes) that the spectrum fails to be a Cantor set, and use this hypothesis to obtain additional Lipschitz control on the spectrum (as a function of the frequency
), which they can then use (after much effort) to improve existing arguments and conclude that the spectrum was in fact Cantor after all!
Manjul Bhargava produces amazingly beautiful mathematics, though most of it is outside of my own area of expertise. One part of his work that touches on an area of my own interest (namely, random matrix theory) is his ongoing work with many co-authors on modeling (both conjecturally and rigorously) the statistics of various key number-theoretic features of elliptic curves (such as their rank, their Selmer group, or their Tate-Shafarevich groups). For instance, with Kane, Lenstra, Poonen, and Rains, Manjul has proposed a very general random matrix model that predicts all of these statistics (for instance, predicting that the -component of the Tate-Shafarevich group is distributed like the cokernel of a certain random
-adic matrix, very much in the spirit of the Cohen-Lenstra heuristics discussed in this previous post). But what is even more impressive is that Manjul and his coauthors have been able to verify several non-trivial fragments of this model (e.g. showing that certain moments have the predicted asymptotics), giving for the first time non-trivial upper and lower bounds for various statistics, for instance obtaining lower bounds on how often an elliptic curve has rank
or rank
, leading most recently (in combination with existing work of Gross-Zagier and of Kolyvagin, among others) to his amazing result with Skinner and Zhang that at least
of all elliptic curves over
(ordered by height) obey the Birch and Swinnerton-Dyer conjecture. Previously it was not even known that a positive proportion of curves obeyed the conjecture. This is still a fair ways from resolving the conjecture fully (in particular, the situation with the presumably small number of curves of rank
and higher is still very poorly understood, and the theory of Gross-Zagier and Kolyvagin that this work relies on, which was initially only available for
, has only been extended to totally real number fields thus far, by the work of Zhang), but it certainly does provide hope that the conjecture could be within reach in a statistical sense at least.
Martin Hairer works in at the interface between probability and partial differential equations, and in particular in the theory of stochastic differential equations (SDEs). The result of his that is closest to my own interests is his remarkable demonstration with Jonathan Mattingly of unique invariant measure for the two-dimensional stochastically forced Navier-Stokes equation
on the two-torus , where
is a Gaussian field that forces a fixed set of frequencies. It is expected that for any reasonable choice of initial data, the solution to this equation should asymptotically be distributed according to Kolmogorov’s power law, as discussed in this previous post. This is still far from established rigorously (although there are some results in this direction for dyadic models, see e.g. this paper of Cheskidov, Shvydkoy, and Friedlander). However, Hairer and Mattingly were able to show that there was a unique probability distribution to almost every initial data would converge to asymptotically; by the ergodic theorem, this is equivalent to demonstrating the existence and uniqueness of an invariant measure for the flow. Existence can be established using standard methods, but uniqueness is much more difficult. One of the standard routes to uniqueness is to establish a “strong Feller property” that enforces some continuity on the transition operators; among other things, this would mean that two ergodic probability measures with intersecting supports would in fact have a non-trivial common component, contradicting the ergodic theorem (which forces different ergodic measures to be mutually singular). Since all ergodic measures for Navier-Stokes can be seen to contain the origin in their support, this would give uniqueness. Unfortunately, the strong Feller property is unlikely to hold in the infinite-dimensional phase space for Navier-Stokes; but Hairer and Mattingly develop a clean abstract substitute for this property, which they call the asymptotic strong Feller property, which is again a regularity property on the transition operator; this in turn is then demonstrated by a careful application of Malliavin calculus.
Maryam Mirzakhani has mostly focused on the geometry and dynamics of Teichmuller-type moduli spaces, such as the moduli space of Riemann surfaces with a fixed genus and a fixed number of cusps (or with a fixed number of boundaries that are geodesics of a prescribed length). These spaces have an incredibly rich structure, ranging from geometric structure (such as the Kahler geometry given by the Weil-Petersson metric), to dynamical structure (through the action of the mapping class group on this and related spaces), to algebraic structure (viewing these spaces as algebraic varieties), and are thus connected to many other objects of interest in geometry and dynamics. For instance, by developing a new recursive formula for the Weil-Petersson volume of this space, Mirzakhani was able to asymptotically count the number of simple prime geodesics of length up to some threshold in a hyperbolic surface (or more precisely, she obtained asymptotics for the number of such geodesics in a given orbit of the mapping class group); the answer turns out to be polynomial in
, in contrast to the much larger class of non-simple prime geodesics, whose asymptotics are exponential in
(the “prime number theorem for geodesics”, developed in a classic series of works by Delsart, Huber, Selberg, and Margulis); she also used this formula to establish a new proof of a conjecture of Witten on intersection numbers that was first proven by Kontsevich. More recently, in two lengthy papers with Eskin and with Eskin-Mohammadi, Mirzakhani established rigidity theorems for the action of
on such moduli spaces that are close analogues of Ratner’s celebrated rigidity theorems for unipotently generated groups (discussed in this previous blog post). Ratner’s theorems are already notoriously difficult to prove, and rely very much on the polynomial stability properties of unipotent flows; in this even more complicated setting, the unipotent flows are no longer tractable, and Mirzakhani instead uses a recent “exponential drift” method of Benoist and Quint as a substitute. Ratner’s theorems are incredibly useful for all sorts of problems connected to homogeneous dynamics, and the analogous theorems established by Mirzakhani, Eskin, and Mohammadi have a similarly broad range of applications, for instance in counting periodic billiard trajectories in rational polygons.

48 comments
Comments feed for this article
12 August, 2014 at 11:32 pm
johngg
You wrote about the medalists 4 years ago not last year.
[Corrected, thanks – T.]
13 August, 2014 at 2:13 am
zr9558
Reblogged this on ZHANG RONG.
13 August, 2014 at 2:33 am
Media Item from “Haaretz” Today: “For the first time ever…” | Combinatorics and more
[…] The ICM 2014 started today in Seoul. The International congress taking place once every four years is an exciting event, celebrated by thousands of mathematicians in Seoul and many others all over the world. The opening ceremonies came with the announcement of Artur Avila, Manjul Bhargava, Martin Hairer, and Maryam Mirzakhani as 2014 Fields medalist, Subhash Khot won the Nevanlinna prize, Stanley Osher won the Gauss prize and Phillip Griffiths is the Chern medalist, and Adrián Paenza won the Leelavati Prize. Heartly congratulations to Artur, Manjul, Martin, Maryam, Subhash, Stanley, Phillip, and Adrián! This is also the first for Brazil and Iran! More on the Fields medalists works can be found on Terry Tao’s blog. […]
13 August, 2014 at 3:33 am
Gabriel
Impressive that 3 of the 4 winners represent important milestones:
First women + Iranian + Middle Eastern winner.
First Brazilian + Latin American winner.
First ethnic Indian winner.
Hairer is also the first Austrian winner, to my knowledge. :)
Hopefully an auspicious sign of things to come.
In addition, 2 of the 4 winners this year were former IMO medalists, giving another boost to the IMO’s prestige. It’ll be interesting to see which standout IMO participants from recent years follow in their footsteps. Lisa Sauermann? Teodor von Burg? Raúl Arturo Chávez Sarmiento? Jeck Lim?
14 August, 2014 at 10:09 am
william e emba
Lindenstrauss was the first Middle Eastern winner.
2 January, 2016 at 4:24 pm
Anonymous
Indian -Canadian/American, best of both worlds. But still brought up through the American system
13 August, 2014 at 4:53 am
Szilard
“First women + Iranian + Middle Eastern winner.
First Brazilian + Latin American winner.
First ethnic Indian winner. ”
I really hope that they have achieved something extraordinary that’s why they gor the award.
Giving an award based on gender and location is a very bad thing.
13 August, 2014 at 6:21 am
Scons Dut
You have seen by yourself that they did, indeed, achieve extraordinary things. There is nothing worrying in enjoying the mentionned facts.
13 August, 2014 at 4:39 pm
Gabriel
Please don’t make ignorant comments like this. All four of the 2014 medalists have been favorites among experts for years and have sterling research records. All of them have previously received many laurels for their contributions; Mirzakhani has won the AMS prize and Clay Award; Avila has won the EMS prize, and so on.
The Fields Medal selection process is about as meritocratic as such an award can be, and probably less clouded by political considerations than the Nobels for the hard sciences. I’ve yet to meet any reputable mathematician who thinks this year’s winners are undeserving.
18 October, 2014 at 3:52 pm
Mo Beans
Not sure if Tao’s already linked to these, but here are good lay-friendly press releases of the Fields winners along with their research if you’re still interested in knowing whether “they’ve achieved something extraordinary”:
Artur Avila (http://www.quantamagazine.org/20140812-a-brazilian-wunderkind-who-calms-chaos/)
Manjul Bhargava (http://www.quantamagazine.org/20140812-the-musical-magical-number-theorist/)
Martin Hairer (http://www.quantamagazine.org/20140812-in-mathematical-noise-one-who-heard-music/)
Maryam Mirzakhani (http://www.quantamagazine.org/20140812-a-tenacious-explorer-of-abstract-surfaces/)
They detail what the winners accomplished aside from what Tao covered above in his post (leaving out of course the mathematical details – broad conceptual brushstrokes are unavoidable if you’re writing for a nontechnical audience), so they should be interesting. Make no mistake, the quality of these winners’ publications are of the highest order. That they happen to be of X nationality and Y gender seems to me almost incidental, and rather irrelevant to the prize committee’s decision to award them the Fields.
13 August, 2014 at 5:54 am
Anonymous
Why not Ben Green? Jacob Lurie (at least he got $3 mil)?
15 August, 2014 at 4:47 pm
Anonymous
Giving Fields to Ben Green is like giving the second medal to Terry Tao. It is indeed slightly disappointing that Jacob Lurie has been passed over, since his insights and achievements certainly do not pale in the view of those of the current medalists.
13 August, 2014 at 8:15 am
Anonymous
Dear Terry, in your (nice!) description of Artur Ávila’s work, you use both and
and 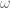 for the phase in the potential for the almost Mathieu operator, it seems. [Corrected, thanks – T.]
for the phase in the potential for the almost Mathieu operator, it seems. [Corrected, thanks – T.]
13 August, 2014 at 8:51 am
meditationatae
In dynamics of billiard balls on polygonal tables, Mirzakhani, Eskin, and Mohammadi apply their theorems to counting periodic billiard trajectories if the polygon is rational ; what part or parts of their hypotheses or theorems don’t go through for non-rational polygons?
13 August, 2014 at 9:12 am
Terence Tao
I’m not an expert on these things, but on looking through the relevant papers it appears that one needs the polygons to have angles commensurate with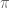 in order to associate such a polygon to a “flat surface” – a Riemann surface with a holomorphic 1-form whose zeroes have some integer multiplicity. (It looks like this construction goes back to a 1974 paper of Zemlyatov and Katok, and seems to basically arise from “unfolding” the polygon under reflections.) If one tries the same construction when one does not have angles commensurate with
in order to associate such a polygon to a “flat surface” – a Riemann surface with a holomorphic 1-form whose zeroes have some integer multiplicity. (It looks like this construction goes back to a 1974 paper of Zemlyatov and Katok, and seems to basically arise from “unfolding” the polygon under reflections.) If one tries the same construction when one does not have angles commensurate with 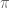 , it looks like one gets some nasty space instead that is somewhat worse than an orbifold, and I don’t know to what extent the methods in these papers carry over to such a setting.
, it looks like one gets some nasty space instead that is somewhat worse than an orbifold, and I don’t know to what extent the methods in these papers carry over to such a setting.
13 August, 2014 at 11:39 am
Anonymous
One can think of the unfolding construction as adding a copy of the table for each of the directions that a billiard ball could be traveling after bouncing off some number of sides. In other words, you want a copy of the table for each element
of the table for each element  in the group
in the group  generated by the linear parts (aka derivatives) of reflections through the sides of the table. You then glue side
generated by the linear parts (aka derivatives) of reflections through the sides of the table. You then glue side  of
of  to side
to side  of
of 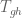 if
if  corresponds to reflection through side
corresponds to reflection through side  . In this way one obtains a surface. The group
. In this way one obtains a surface. The group  is finite exactly when the angles are all rational multiplies of
is finite exactly when the angles are all rational multiplies of 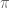 . So in these cases, the unfolding construction gives a nice compact surface. When
. So in these cases, the unfolding construction gives a nice compact surface. When  is infinite, the surface will not be compact, which is harder to work with, and so the construction is much less useful. The rational angle condition is not really so natural if you’re interested in general billiards. There are, however, a few results for general tables that can be proved by approximating by rational tables, for which the unfolding construction is fruitful.
is infinite, the surface will not be compact, which is harder to work with, and so the construction is much less useful. The rational angle condition is not really so natural if you’re interested in general billiards. There are, however, a few results for general tables that can be proved by approximating by rational tables, for which the unfolding construction is fruitful.
13 August, 2014 at 10:55 am
2014 Fields Medal and Nevanlinna Prize Winners Announced
[…] Terry Tao (previous Fields Medal Winner): Avila, Bhargava, Hairer, Mirzakhani […]
13 August, 2014 at 12:17 pm
Mark Meckes
The list of tags on this post made me notice the utterly meaningless coincidence that this year’s medalists’ names are in the same order whether you alphabetize by first names or by last names.
13 August, 2014 at 1:37 pm
James
Nontrivial observation considering all the Ma*s.
13 August, 2014 at 3:29 pm
Khot, Osher, Griffiths | What's new
[…] addition to the Fields medallists mentioned in the previous post, the IMU also awarded the Nevanlinna prize to Subhash Khot, the Gauss prize to Stan Osher (my […]
13 August, 2014 at 4:24 pm
Gabriel
I forgot to mention that Artur Avila is also the first Fields Medalist to receive his doctorate outside of the U.S. or Europe. He was educated from beginning to end in his native Brazil. What a coup for Brazil’s IMPA.
14 August, 2014 at 12:46 am
Gergely
There are counterexamples to what you say: Kodaira (Tokyo), Mori (Kyoto), Zelmanov (Novisibirsk), Lindenstrauss (Jerusalem).
14 August, 2014 at 6:58 pm
John
The guy was also a prodigy. He won an gold medal at the IMO and got his Phd. from the best pure and applied math institution in Brazil at 21.
14 August, 2014 at 11:08 am
Fields Medals 2014 | physics4me
[…] also: Avila, Bhargava, Hairer, Mirzakhani by Terence […]
15 August, 2014 at 3:43 am
Terrance Tao discusses the Fields Medal winners. | BUMPS
[…] addition to the Fields medallists mentioned in the previous post, the IMU also awarded the Nevanlinna prize to Subhash Khot, the Gauss prize to Stan Osher (my […]
15 August, 2014 at 9:29 am
Medallas Fields 2014, IMO 1995 y software para Mac | Adsu's Blog
[…] de descubrir, en esta entrada de Tao, unos vídeos sobre los medallistas Fields del […]
15 August, 2014 at 10:21 am
Día importante para las Matemáticas: Maryam Mirzakhani (Irán) gana una Medalla Fields | Ciencia | La Ciencia de la Mula Francis
[…] leer a Terence Tao, “Avila, Bhargava, Hairer, Mirzakhani,” What’s New, 12 Aug 2014, y “Khot, Osher, Griffiths,” What’s New, 12 Aug 2014. Tim Gowers, “ICM2014 […]
15 August, 2014 at 4:55 pm
Anonymous
Bhargava’s 66% BSD contribution to our understanding of the BSD conjecture seems to be a red herring: Bhargava’s result does not prove BSD for a single elliptic curve for which it was not known already by much deeper work of other authors (Gross-Zagier, Kolyvagin, Wei Zhang)! Bhargava simply puts known results together under an appealingly-looking average statement, which in practice is of rather limited use.
16 August, 2014 at 4:32 am
Cynicism
This is ridiculous. Before Bhargava’s work we knew basically nothing about the average rank of elliptic curves unconditionally. If you want to say that Bhargava’s work doesn’t tell us much about BSD for any single elliptic curve then both he and I would probably agree with you. But to say there’s limited use for knowing the average behavior of difficult-to-know quantities is unthinkable for any mathematician or math enthusiast.
16 August, 2014 at 5:00 am
Anonymous
I think you misunderstood my comment. I agree that the average rank information that he provides is very much of interest. The thing that I do not agree with is that this is any substantial progress towards BSD (the description of his work in the text calls the 66% aspect “one of the best results we have on BSD”). In particular, I think that the 66% aspect (which is Bhargava’s contribution) is of no practical use for BSD. Bhargava’s average rank work is surely substantial progress towards another problem in the arithmetic of elliptic curves (of completely different flavor), namely, the Katz-Sarnak 50-50 conjecture. But to me it doesn’t seem appropriate to use the 66% BSD as a selling point of Bhargava’s results, because the 66% is just repackaging of deeper results of others. Unfortunately, this was done even in the laudatio (although quite mildly).
17 August, 2014 at 7:07 am
Terence Tao
I admit I made a poor choice of words with “best result we have”; I was thinking in the technical sense used by analytic number theorists, in which “best” means “largest lower bound available” or “smallest upper bound available”, and not in the colloquial sense. (This problem of a scientific term being mistaken for a public meaning is pervasive in science, and I guess it caught me out too this time. I vaguely remember thinking while initially writing this post that I would use “one of the best” rather than “best” to indicate that I was only interpreting “best” in a narrow sense, but that clearly didn’t work out as intended.) I’ve reworded the post to remove this confusion (and also incorporated some other corrections sent to me by email).
(Added later) I agree that statistical results on BSD do not provide any obvious way forward to resolve the full BSD conjecture, but such statistical results may still be eventually useful in some analytic number theory applications as a partial substitute for the full BSD conjecture, in analogy to how the Bombieri-Vinogradov theorem (“GRH on the average”) is a useful substitute for actual GRH, or the density hypothesis (“RH is true for most zeroes of zeta”) is a useful substitute for actual RH. Presumably one needs to make further advances on the analytic rank side of BSD as well as the algebraic rank side of BSD to get to this point, though.
16 August, 2014 at 5:25 am
2014 Fields Medals | Not Even Wrong
[…] For two very different sorts of blog posts about the Fields Medal, see Terry Tao and […]
16 August, 2014 at 10:28 am
Fields Medals 2014 | babis' blog
[…] summarizes some of their scientific contributions. Terence Tao wrote a more technical article-post about this year’s […]
16 August, 2014 at 7:20 pm
Anonymous
Looking at some of the semi-popular-press stuff about the medalists’ work, Hairer seems to have done some new formalization of stochastic PDE that allowed mathematically rigorous treatment of stuff that previously was done only hand-wavingly by physicists. Can anyone describe what that was about and what difficulty was overcome? I thought this stuff went back to Wiener’s explanation of Brownian motion in the 1930’s. Is there a generally accessible introduction to the subject? It does sound interesting. Thanks.
18 August, 2014 at 11:04 am
Anonymous
The basic idea is that solutions to many physical SPDEs cannot have sufficient regularity to be classical, because the white noise which forces the system is not a function. If the SPDE is either linear or close to linear, this can be overcome by using some version of the theory of distributions or other classical techniques. Hairer’s work allows one to tackle SPDEs that are highly non-linear, such as the KPZ equation. One of the terms in this equation is the square of a gradient: since solutions typically only exist in the distributional sense it is not clear how one should make sense of this term. Hairer developed a framework called “Regularity structures” which one can think of as a generalization of Taylor approximations that allows one to prove well-posedness of equations of this type.
The most generally accessible introduction to this field (which is extremely new) currently available is probably this: http://arxiv.org/pdf/1401.3014v2.pdf
2 September, 2014 at 5:34 am
Olivier
“and the theory of Gross-Zagier and Kolyvagin that this work relies on is not available for other number fields than {{\bf Q}}”
In fact, it is valid over all totally real fields (albeit with complications).
[Thanks for the correction! – T.]
3 September, 2014 at 8:19 pm
Maryam Mirzakhani and Dynamics on Moduli Space | A Hitchhiker's Guide to the Ivory Tower
[…] by Terence Tao and […]
17 June, 2017 at 11:49 am
FIELDS MEDAL 2018
Who do you think will win the Fields Medal in 2018? Vote here (choose four names): https://poll.pollcode.com/44839318
24 June, 2017 at 10:53 am
FIELDS MEDAL 2018
Besides Peter Scholze, who do you think will win the Fields Medal in 2018 (choose up to three names)? Vote here: https://vote.pollcode.com/31229277
7 July, 2017 at 5:00 am
FIELDS MEDAL 2018
The final round of voting for the Fields Medal 2018: https://vote.pollcode.com/73641394
First round results: https://poll.pollcode.com/44839318_result
Second round results: https://poll.pollcode.com/31229277_result
15 July, 2017 at 10:21 am
Maryam Mirzakhani | What's new
[…] she won the Fields medal in 2014 (as I posted about previously on this blog), we corresponded for a while. The Fields medal is of course one of the highest honours one can […]
15 July, 2017 at 10:57 am
The unprecedented Best Seller! | My Blog
[…] she won the Fields medal in 2014 (as I posted about previously on this blog), we corresponded for a while. The Fields medal is of course one of the highest honours one can […]
15 July, 2017 at 2:14 pm
Jemas Kumar
Reblogged this on Jemas Kumar.
19 July, 2017 at 12:18 am
Anonymous
typo: In the last paragraph the word “with” should be removed from the sentence ending “…Benoist and Quint with as a substitute.”
[Corrected, thanks – T.]
22 July, 2017 at 1:48 am
some published posts about Maryam Mirzakhani | Mathpresso
[…] she won the Fields medal in 2014 (as I posted about previously on this blog), we corresponded for a while. The Fields medal is of course one of the highest honours one can […]
5 May, 2018 at 10:09 am
some published posts about Maryam Mirzakhani – Pangan 7
[…] she won the Fields medal in 2014 (as I posted about previously on this blog), we corresponded for a while. The Fields medal is of course one of the highest honours one can […]
1 August, 2018 at 9:01 am
Birkar, Figalli, Scholze, Venkatesh | What's new
[…] the two previous congresses in 2010 and 2014, I wrote blog posts describing some of the work of each of the winners. This time, though, I happened to be a member […]
17 July, 2020 at 12:50 pm
Some published posts about Maryam Mirzakhani | Diranlou
[…] she won the Fields medal in 2014 (as I posted about previously on this blog), we corresponded for a while. The Fields medal is of course one of the highest honours one can […]