In graph theory, the recently developed theory of graph limits has proven to be a useful tool for analysing large dense graphs, being a convenient reformulation of the Szemerédi regularity lemma. Roughly speaking, the theory asserts that given any sequence of finite graphs, one can extract a subsequence
which converges (in a specific sense) to a continuous object known as a “graphon” – a symmetric measurable function
. What “converges” means in this context is that subgraph densities converge to the associated integrals of the graphon
. For instance, the edge density
converge to the integral
the triangle density
converges to the integral
the four-cycle density
converges to the integral
and so forth. One can use graph limits to prove many results in graph theory that were traditionally proven using the regularity lemma, such as the triangle removal lemma, and can also reduce many asymptotic graph theory problems to continuous problems involving multilinear integrals (although the latter problems are not necessarily easy to solve!). See this text of Lovasz for a detailed study of graph limits and their applications.
One can also express graph limits (and more generally hypergraph limits) in the language of nonstandard analysis (or of ultraproducts); see for instance this paper of Elek and Szegedy, Section 6 of this previous blog post, or this paper of Towsner. (In this post we assume some familiarity with nonstandard analysis, as reviewed for instance in the previous blog post.) Here, one starts as before with a sequence of finite graphs, and then takes an ultraproduct (with respect to some arbitrarily chosen non-principal ultrafilter
) to obtain a nonstandard graph
, where
is the ultraproduct of the
, and similarly for the
. The set
can then be viewed as a symmetric subset of
which is measurable with respect to the Loeb
-algebra
of the product
(see this previous blog post for the construction of Loeb measure). A crucial point is that this
-algebra is larger than the product
of the Loeb
-algebra of the individual vertex set
. This leads to a decomposition
where the “graphon” is the orthogonal projection of
onto
, and the “regular error”
is orthogonal to all product sets
for
. The graphon
then captures the statistics of the nonstandard graph
, in exact analogy with the more traditional graph limits: for instance, the edge density
(or equivalently, the limit of the along the ultrafilter
) is equal to the integral
where denotes Loeb measure on a nonstandard finite set
; the triangle density
(or equivalently, the limit along of the triangle densities of
) is equal to the integral
and so forth. Note that with this construction, the graphon is living on the Cartesian square of an abstract probability space
, which is likely to be inseparable; but it is possible to cut down the Loeb
-algebra on
to minimal countable
-algebra for which
remains measurable (up to null sets), and then one can identify
with
, bringing this construction of a graphon in line with the traditional notion of a graphon. (See Remark 5 of this previous blog post for more discussion of this point.)
Additive combinatorics, which studies things like the additive structure of finite subsets of an abelian group
, has many analogies and connections with asymptotic graph theory; in particular, there is the arithmetic regularity lemma of Green which is analogous to the graph regularity lemma of Szemerédi. (There is also a higher order arithmetic regularity lemma analogous to hypergraph regularity lemmas, but this is not the focus of the discussion here.) Given this, it is natural to suspect that there is a theory of “additive limits” for large additive sets of bounded doubling, analogous to the theory of graph limits for large dense graphs. The purpose of this post is to record a candidate for such an additive limit. This limit can be used as a substitute for the arithmetic regularity lemma in certain results in additive combinatorics, at least if one is willing to settle for qualitative results rather than quantitative ones; I give a few examples of this below the fold.
It seems that to allow for the most flexible and powerful manifestation of this theory, it is convenient to use the nonstandard formulation (among other things, it allows for full use of the transfer principle, whereas a more traditional limit formulation would only allow for a transfer of those quantities continuous with respect to the notion of convergence). Here, the analogue of a nonstandard graph is an ultra approximate group in a nonstandard group
, defined as the ultraproduct of finite
-approximate groups
for some standard
. (A
-approximate group
is a symmetric set containing the origin such that
can be covered by
or fewer translates of
.) We then let
be the external subgroup of
generated by
; equivalently,
is the union of
over all standard
. This space has a Loeb measure
, defined by setting
whenever is an internal subset of
for any standard
, and extended to a countably additive measure; the arguments in Section 6 of this previous blog post can be easily modified to give a construction of this measure.
The Loeb measure is a translation invariant measure on
, normalised so that
has Loeb measure one. As such, one should think of
as being analogous to a locally compact abelian group equipped with a Haar measure. It should be noted though that
is not actually a locally compact group with Haar measure, for two reasons:
- There is not an obvious topology on
that makes it simultaneously locally compact, Hausdorff, and
-compact. (One can get one or two out of three without difficulty, though.)
- The addition operation
is not measurable from the product Loeb algebra
to
. Instead, it is measurable from the coarser Loeb algebra
to
(compare with the analogous situation for nonstandard graphs).
Nevertheless, the analogy is a useful guide for the arguments that follow.
Let denote the space of bounded Loeb measurable functions
(modulo almost everywhere equivalence) that are supported on
for some standard
; this is a complex algebra with respect to pointwise multiplication. There is also a convolution operation
, defined by setting
whenever ,
are bounded nonstandard functions (extended by zero to all of
), and then extending to arbitrary elements of
by density. Equivalently,
is the pushforward of the
-measurable function
under the map
.
The basic structural theorem is then as follows.
Theorem 1 (Kronecker factor) Let
be an ultra approximate group. Then there exists a (standard) locally compact abelian group
of the form
for some standard
and some compact abelian group
, equipped with a Haar measure
and a measurable homomorphism
(using the Loeb
-algebra on
and the Baire
-algebra on
), with the following properties:
- (i)
has dense image, and
is the pushforward of Loeb measure
by
.
- (ii) There exists sets
with
open and
compact, such that
- (iii) Whenever
with
compact and
open, there exists a nonstandard finite set
such that
- (iv) If
, then we have the convolution formula
where
are the pushforwards of
to
, the convolution
on the right-hand side is convolution using
, and
is the pullback map from
to
. In particular, if
, then
for all
.
One can view the locally compact abelian group as a “model “or “Kronecker factor” for the ultra approximate group
(in close analogy with the Kronecker factor from ergodic theory). In the case that
is a genuine nonstandard finite group rather than an ultra approximate group, the non-compact components
of the Kronecker group
are trivial, and this theorem was implicitly established by Szegedy. The compact group
is quite large, and in particular is likely to be inseparable; but as with the case of graphons, when one is only studying at most countably many functions
, one can cut down the size of this group to be separable (or equivalently, second countable or metrisable) if desired, so one often works with a “reduced Kronecker factor” which is a quotient of the full Kronecker factor
. Once one is in the separable case, the Baire sigma algebra is identical with the more familiar Borel sigma algebra.
Given any sequence of uniformly bounded functions for some fixed
, we can view the function
defined by
as an “additive limit” of the , in much the same way that graphons
are limits of the indicator functions
. The additive limits capture some of the statistics of the
, for instance the normalised means
converge (along the ultrafilter ) to the mean
and for three sequences of functions, the normalised correlation
converges along to the correlation
the normalised Gowers norm
converges along to the
Gowers norm
and so forth. We caution however that some correlations that involve evaluating more than one function at the same point will not necessarily be preserved in the additive limit; for instance the normalised norm
does not necessarily converge to the norm
but can converge instead to a larger quantity, due to the presence of the orthogonal projection in the definition (4) of
.
An important special case of an additive limit occurs when the functions involved are indicator functions
of some subsets
of
. The additive limit
does not necessarily remain an indicator function, but instead takes values in
(much as a graphon
takes values in
even though the original indicators
take values in
). The convolution
is then the ultralimit of the normalised convolutions
; in particular, the measure of the support of
provides a lower bound on the limiting normalised cardinality
of a sumset. In many situations this lower bound is an equality, but this is not necessarily the case, because the sumset
could contain a large number of elements which have very few (
) representations as the sum of two elements of
, and in the limit these portions of the sumset fall outside of the support of
. (One can think of the support of
as describing the “essential” sumset of
, discarding those elements that have only very few representations.) Similarly for higher convolutions of
. Thus one can use additive limits to partially control the growth
of iterated sumsets of subsets
of approximate groups
, in the regime where
stays bounded and
goes to infinity.
Theorem 1 can be proven by Fourier-analytic means (combined with Freiman’s theorem from additive combinatorics), and we will do so below the fold. For now, we give some illustrative examples of additive limits.
Example 2 (Bohr sets) We take
to be the intervals
, where
is a sequence going to infinity; these are
-approximate groups for all
. Let
be an irrational real number, let
be an interval in
, and for each natural number
let
be the Bohr set
In this case, the (reduced) Kronecker factor
can be taken to be the infinite cylinder
with the usual Lebesgue measure
. The additive limits of
and
end up being
and
, where
is the finite cylinder
and
is the rectangle
Geometrically, one should think of
and
as being wrapped around the cylinder
via the homomorphism
, and then one sees that
is converging in some normalised weak sense to
, and similarly for
and
. In particular, the additive limit predicts the growth rate of the iterated sumsets
to be quadratic in
until
becomes comparable to
, at which point the growth transitions to linear growth, in the regime where
is bounded and
is large.
If
were rational instead of irrational, then one would need to replace
by the finite subgroup
here.
Example 3 (Structured subsets of progressions) We take
be the rank two progression
where
is a sequence going to infinity; these are
-approximate groups for all
. Let
be the subset
Then the (reduced) Kronecker factor can be taken to be
with Lebesgue measure
, and the additive limits of the
and
are then
and
, where
is the square
and
is the circle
Geometrically, the picture is similar to the Bohr set one, except now one uses a Freiman homomorphism
for
to embed the original sets
into the plane
. In particular, one now expects the growth rate of the iterated sumsets
and
to be quadratic in
, in the regime where
is bounded and
is large.
Example 4 (Dissociated sets) Let
be a fixed natural number, and take
where
are randomly chosen elements of a large cyclic group
, where
is a sequence of primes going to infinity. These are
-approximate groups. The (reduced) Kronecker factor
can (almost surely) then be taken to be
with counting measure, and the additive limit of
is
, where
and
is the standard basis of
. In particular, the growth rates of
should grow approximately like
for
bounded and
large.
Example 5 (Random subsets of groups) Let
be a sequence of finite additive groups whose order is going to infinity. Let
be a random subset of
of some fixed density
. Then (almost surely) the Kronecker factor here can be reduced all the way to the trivial group
, and the additive limit of the
is the constant function
. The convolutions
then converge in the ultralimit (modulo almost everywhere equivalence) to the pullback of
; this reflects the fact that
of the elements of
can be represented as the sum of two elements of
in
ways. In particular,
occupies a proportion
of
.
Example 6 (Trigonometric series) Take
for a sequence
of primes going to infinity, and for each
let
be an infinite sequence of frequencies chosen uniformly and independently from
. Let
denote the random trigonometric series
Then (almost surely) we can take the reduced Kronecker factor
to be the infinite torus
(with the Haar probability measure
), and the additive limit of the
then becomes the function
defined by the formula
In fact, the pullback
is the ultralimit of the
. As such, for any standard exponent
, the normalised
norm
can be seen to converge to the limit
The reader is invited to consider combinations of the above examples, e.g. random subsets of Bohr sets, to get a sense of the general case of Theorem 1.
It is likely that this theorem can be extended to the noncommutative setting, using the noncommutative Freiman theorem of Emmanuel Breuillard, Ben Green, and myself, but I have not attempted to do so here (see though this recent preprint of Anush Tserunyan for some related explorations); in a separate direction, there should be extensions that can control higher Gowers norms, in the spirit of the work of Szegedy.
Note: the arguments below will presume some familiarity with additive combinatorics and with nonstandard analysis, and will be a little sketchy in places.
— 1. Proof of theorem —
By Freiman’s theorem for arbitrary abelian groups (see this paper of Green and Ruzsa), we can find an ultra coset progression such that
for some standard ; we abbreviate the latter inclusion as
. By an ultra coset progression, we mean the sumset of a nonstandard finite group
and a nonstandard generalised arithmetic progression
with (known as the rank) standard, the generators
in
and the dimensions
being nonstandard natural numbers. (To get the containment
, one can first use the Bogulybov lemma to get a large ultra coset progression
inside
, so that
can be covered by
translates of
; one can then add these translates to the generators of
to obtain an ultra coset progression
with the required properties.
We call the ultra coset progression -proper if the sums
for
and
for
are all distinct. If
fails to be
-proper, then we can find a containment
where the coset progression has strictly smaller rank than
; see e.g. Lemma 5.1 of this paper of Van Vu and myself). Iterating this fact, we see that we may assume without loss of generality that
is
-proper. In particular, the group
can now be parameterised by the sums
with
for
, with each element of
having exactly one representation of this form.
The dimensions are either bounded (and thus standard natural numbers) or unbounded. After permuting the generators if necessary, we may assume that
are unbounded and
are bounded for some
with
. We then have an external surjective group homomorphism
defined by
this will end up being the non-compact portion of the projection map that we will eventually construct. The image
is precompact in
(in fact it is compact, thanks to countable saturation).
Now we perform some Fourier analysis on (analogous to the usual theory of Fourier analysis on locally compact abelian groups). Define a frequency to be a measurable homomorphism
from
to
, and let
denote the space of such frequencies; this is an additive group, which should be thought of as a “Pontryagin dual” to
(even though
is not a locally compact group). Meanwhile, we have the (genuine) Pontryagin dual
of
, using the identification
The homomorphism then induces a dual homomorphism
, defined by the formula
for all and
. This homomorphism
is easily seen to be injective. If we let
denote the cokernel of this map, then
is an abelian group (which we will view as a discrete group) and we have the short exact sequence
Observe that is a divisible group. From this and a Zorn’s lemma argument we can split this short exact sequence, lifting
up to a subgroup
of
, so that the latter group can be viewed as the direct sum of
and
.
Let be the Pontryagin dual of
, that is to say the space of all homomorphisms
from
to
(with no measurability or continuity hypotheses imposed). This is a compact abelian group (it is a closed subset of
, which is compact by Tychonoff’s theorem). Set
. We have a homomorphism
, defined by
We claim that has dense image. Since
is surjective, it suffices to show that the map from
to
has dense image from
to
, where
is the kernel of . The closure of the image of
is a compact subgroup of
, so this map did not have dense image, there would exist a non-trivial
in the Pontryagin dual
of
which annihilates all of
. The map
then factors through
and thus can be identified with an element of
; but
and
only intersect at
, a contradiction. Thus
has dense image.
It is a routine matter to verify that is measurable (noting that the Baire algebra is generated by the product of measurable sets in
and cylinder sets in
), that
is precompact, and that the inverse image of any compact set is contained in
for some standard
. From this and the Riesz representation theorem, we can define a Haar measure
on
by defining
for all continuous, compactly supported functions ; the translation invariance of this measure follows from the surjectivity of
. From Urysohn’s lemma and the inner and outer regularity of Haar measures, one can then show that
is the pushforward of Loeb measure
under
.
Now we show the convolution property (3). First suppose that , which in particular implies that
for all , since the function
factors through
. By the Loeb measure construction, we can write
as the limit (in
) of functions
, where
are uniformly bounded nonstandard functions and
is some standard natural number. Then we have
which in particular implies that
where ranges over all nonstandard maps
of the form
for some and nonstandard homomorphism
. From (nonstandard) Fourier analysis, we conclude that
for any bounded nonstandard function , or equivalently that
and thus on taking limits we see that , and on taking further limits we see that
for any
, as required. This proves (3) when
; similarly when
. To finish off the general case of (3), it suffices to show that
for bounded measurable . By Fourier decomposition, we may assume that
takes the form
for some and some continuous compactly supported
, and similarly
for some and continuous compactly supported
.
If , then
for some
, and one can use this to show that
and
both vanish. Thus we may assume that
; using modulation symmetry we may then assume that
. It thus suffices to show that
A direct calculation shows that the left and right hand sides agree up to constants; but both sides also have integral when integrated against
, so they must agree identically.
Now, we prove the inclusions (1). The outer inclusion comes from the compactness (or precompactness) of
. For the inner inclusion, we note from (3) and the positive measure and symmetry of
that
is the pullback
of a continuous function on
that is positive at the origin, and thus also bounded away from zero on a neighbourhood
of the origin. This implies that the set
has full measure in
. We then let
be a smaller symmetric neighbourhood of the origin such that
. We then see that for any
, the sets
and
both have full measure in
, and hence
lies in
. This gives the inner inclusion
of (1).
Finally, we show the regularity claim (2). Given , we may apply Urysohn’s lemma to find non-negative bounded continuous functions
such that
is supported in
and is at least
on
. Letting
be the pullbacks of
by
, we conclude using (3) that
is at least
on
and vanishes outside of
. Approximating
in
by bounded nonstandard functions
supported in
, we conclude that
is at least
(say) on
and less than
(say) outside of
. If one then sets
to be the non-standard set where
, we obtain the claim.
— 2. Sample applications of theorem —
In this section we illustrate how this theorem can be used to reprove some existing results in additive combinatorics, reducing them to various statements in continuous harmonic analysis. We begin with a qualitative version of a result of Croot and Sisask on almost periods, which reduces to the classical fact that the convolution of two square-integrable functions is continuous.
Proposition 7 (Croot-Sisask) Let
be a
-approximate group in an additive group
, let
be subsets of
, and let
. Then there exists a subset
of
with
such that
for all
(using the non-normalised convolution
).
The Croot-Sisask argument in fact gives a quantitative lower bound of exponential type on , but such bounds are not available through the qualitative limiting arguments given here. The Croot-Sisask argument also works in non-commutative groups
; it is likely the arguments here would also extend to that setting once one developed a non-commutative version of Theorem 1, but we have not investigated that here.
Proof: By the usual transfer arguments, it suffices to show that when is an ultra approximate group,
are non-standard subsets of
, and
, there exists a nonstandard subset
of
with
such that
for all (using the normalised convolution
). But by (3),
is the pullback via
of a continuous compactly supported function, so (5) holds for
in
for some neighbourhood
of the identity, and thus by (2) it also holds for all
in some nonstandard
of positive Loeb measure. The claim follows.
Now we give a proof of Roth’s theorem (in the averaged form of Varnavides), at least for groups of odd order.
Proposition 8 (Roth’s theorem) Let
, let
be a finite group of odd order, and let
be such that
. Then there are
pairs
such that
.
Proof: By the usual transfer arguments, it suffices to show that when is a nonstandard finite group of odd order, and
is a nonstandard subset of
with
, then there are
pairs
such that
; equivalently, we need to show that
where . As
has positive measure,
is not identically zero. By a version of the Lebesgue differentiation theorem, we can then find a point
in the Kronecker factor group
such that
has positive density on every precompact neighbourhood of
, and is bounded away from zero on a subset of a symmetric open precompact neighbourhood
of
of density greater than
. From this and (3) we see that
is bounded away from zero on almost all of
for some neighbourhood
of
. Also, as
has odd order, the map
is a measure-preserving map on
, it must also be so on
, and so we conclude that
has positive measure in
, and (6) follows.
Finally, we give a more advanced application of additive limits, namely reproving a lemma of Eberhard, Green, and Manners.
Proposition 9 For every
there is
such that if
is such that
, then there is an arithmetic progression
such that
and
.
Proof: Here, we perform the transfer step more explicitly, as it is slightly trickier here. Suppose for contradiction that the claim failed, then there exists an and a sequence
with
but such that there is no arithmetic progression with
such that
. Note that
must go to infinity (otherwise one could take
to consist of a single element of
, which must be non-empty from (7). Taking ultraproducts, we arrive at a nonstandard subset
of
for some unbounded natural number
, such that
and such that there is no nonstandard arithmetic progression with
and
(say). Here
is the Loeb measure associated with the approximate group
and the group
that it generates. By inspection of the proof of Theorem 1, the Kronecker factor of this group can be taken to be
for some compact group
, with projection
given by
for some measurable map
, and Haar measure
given by the product of Lebesgue measure on
and the Haar probability measure
on
. If we let
, then
is supported in
and takes values in
, and from (3) and (8) we see that the set
is such that
We can view as a measurable function
, defined by
, and similarly the indicator function
can be viewed as a measurable function
defined by
. Being measurable,
may be approximated in
by piecewise constant functions. One can then adapt the proof of the Lebesgue differentiation theorem to show that almost all
are a Lebesgue point of
, in the sense that
Similarly, almost all is a Lebesgue point of
in the sense that
From this, we see that for almost all , we have the inclusion
up to null sets in , where the convolution is now with respect to the Haar probability measure
. On the other hand, from Fubini’s theorem we have
and
Also is supported on
. Thus by the pigeonhole principle, we may find an
such that
and such that (9) holds up to null sets, and such that is a Lebesgue point for
. If we fix this
and now set
and
, we thus have
At this point it is convenient to split the compact abelian group as
where is the connected component of the identity, thus
is a totally disconnected group. Let
be the pushforward of
to
via the projection map
, thus
is a measurable function of total integral
. We claim that
To see this, suppose for contradiction that
We may disintegrate
where is a measurable map from
to finite measures on
, such that for almost every
,
is supported on
and has total mass
. For almost every
and
, we then have that
is supported in . By Fubini’s theorem we have
where is the Haar probability measure on
. From (10), we conclude that for almost every
, there is a positive measure set of
such that
for a positive measure set of (in particular
), and that
is supported in
. On the other hand,
and
are supported on sets of measure at least
and
. Applying Kemperman’s theorem (see this previous post) , we conclude that
for almost every with
, and for a positive measure set of
. But this leads to a contradiction if we take
to be within
of the essential supremum of
. This proves (11).
As is totally disconnected, we can express the origin as the intersection of open subgroups. From this, (11), and a Lebesgue differentiation argument, we may find a coset
of an open subgroup
of
such that
Letting be a pullback of
to
, we thus have
Since is a Lebesgue point for
, we may thus find a neighbourhood
of
in
such that
or equivalently
To finish the proof of the claim, it then suffices to show that differs from a nonstandard arithmetic progression by a set of arbitrarily small Loeb measure.
Consider the quotient homomorphism formed by first using
to project
to
, then projecting to
, then to
. This is a Loeb measurable map, and thus the pointwise limit (up to null sets) by a nonstandard function. But observe that for
, one has
if and only if
for almost every
. In particuar, if
is a nonstandard function which is sufficiently close to
, then
if and only if
is the most common value of
for
. Using this, one can find a representative of
that is precisely a nonstandard function on
(say). Thus
is now a nonstandard map from
to the standard finite group
, and from construction one can check that
for all (and not merely almost all)
. From this it is easy to see that
is periodic with some bounded period, and that the level sets of
are infinite nonstandard arithmetic progressions of bounded spacing. The claim then follows.

15 comments
Comments feed for this article
12 October, 2014 at 4:00 pm
Anonymous
A few comments:
* “What “converges” means in this context means that” –> “What “converges” means in this context is that” ” and “
” and “ ”, reps., for absolut values instead of “
”, reps., for absolut values instead of “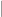 ” to get correct horixontal spacing
” to get correct horixontal spacing ” instead of “
” instead of “ ” to get correct horixontal spacing
” to get correct horixontal spacing
* Use “
* Should there be four integrals instead of three in the sixth displayed expression?
* Use “
[Corrected, thanks – T.]
12 October, 2014 at 4:02 pm
Anonymous
The last comment should be as follows:
* Use “ ” instead of “
” instead of “ ” for maps to get correct horizontal spacing
” for maps to get correct horizontal spacing
13 October, 2014 at 2:52 am
Mike
Click to access 0712.2749.pdf
13 October, 2014 at 12:28 pm
Francisco Javier Thayer
Consider a hyperfinite graph G for which some rescaling of the graph distance of G has the property that its infinitesimal collapse is locally compact. (infinitesimal collapse means the space obtained identifying elements infinitely close to each other — which yields always a complete metric space in which of course distances between points may be infinite). Such a rescaling may not exist, but it does for instance if the graph has polynomial growth for some rescaling. The infinitesimal collapse in this case is a length space and has a natural measure obtained by push-down of Loeb measure. Does this collapse have any relation to the graph-limit construction?
13 October, 2014 at 1:51 pm
Terence Tao
The two limits are analogous, but correspond to different scaling regimes. For the usual graph limits, one works with dense graphs, in which there are vertices for some large
vertices for some large  , and the number of edges is comparable to
, and the number of edges is comparable to 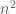 ; in particular, the typical graph distance between two vertices is of the order of
; in particular, the typical graph distance between two vertices is of the order of 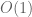 (in fact, unless the graph is pretty much k-partite for some bounded k, the graph distance between most pairs of vertices will be 1 or 2). For the asymptotic cone construction, one works with Cayley graphs in which the number of edges is instead comparable to
(in fact, unless the graph is pretty much k-partite for some bounded k, the graph distance between most pairs of vertices will be 1 or 2). For the asymptotic cone construction, one works with Cayley graphs in which the number of edges is instead comparable to  , and the graph distance between two vertices would be polynomial in
, and the graph distance between two vertices would be polynomial in  (if one is in the polynomial growth case). One then normalises the graph distance to be
(if one is in the polynomial growth case). One then normalises the graph distance to be 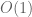 and takes a limit.
and takes a limit.
For bounded degree graphs, there is another notion of graph limit, based on what happens with local neighbourhoods of randomly chosen vertices at graph distance O(1). For Cayley graphs of finitely generated groups, this comes down to taking pointwise limits of the set of relations between generators, for instance with generators
with generators 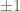 converges in this sense to
converges in this sense to  with the generators
with the generators 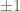 . This would also correspond to the asymptotic cone construction if one did not rescale the metric beforehand.
. This would also correspond to the asymptotic cone construction if one did not rescale the metric beforehand.
14 October, 2014 at 3:02 am
Chris Eagle
“The set ${E_\alpha}$ can then be viewed as a symmetric subset of ${E_\alpha \times E_\alpha}$”: surely ${E_\alpha}$ is a subset of $V_\alpha \times V_\alpha}$?
[Corrected, thanks – T.]
20 October, 2014 at 6:45 am
Sean Eberhard
Dear Terry,
This is a nice way of looking at these things. Has such a soft proof of Roth’s theorem (reduction to Lebesgue differentiation theorem) appeared before? I’ve always wanted to see such a proof.
In the proof of prop 4, by restricting to the symmetric case you get away with just the trivial case of Brunn-Minkowski
you get away with just the trivial case of Brunn-Minkowski  in
in  , but if you wanted a similar result for
, but if you wanted a similar result for 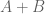 or even
or even 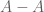 I guess you would actually need to say “Brunn-Minkowski” at some point. In general I tend to think of prop 4 as an incarnation of Brunn-Minkowski. (By the way, in the statement of prop 4 I think you want
I guess you would actually need to say “Brunn-Minkowski” at some point. In general I tend to think of prop 4 as an incarnation of Brunn-Minkowski. (By the way, in the statement of prop 4 I think you want  , not
, not  .)
.)
25 October, 2014 at 6:47 am
Terence Tao
Thanks for the correction!
Regarding Roth’s theorem, certainly the ergodic theory approach to Roth’s theorem can be routed through the Lebesgue differentiation theorem after reducing to the Kronecker factor there, which is also a compact group, and computing the second Host-Kra measure mu^{[2]} on that group. And in the graph theory approach there is an analogous proof (I think in Lovasz’s book, though I don’t have it handy right now) of Roth’s theorem via Lebesgue differentiation on the unit interval [0,1].
27 October, 2014 at 7:39 am
Sean Eberhard
Thanks for the references.
By the way, is it really true in Theorem 1 that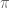 is always surjective? In other words, in the proof, is it really true that the image of
is always surjective? In other words, in the proof, is it really true that the image of 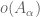 is a compact subgroup of
is a compact subgroup of  ? I do agree that the image of
? I do agree that the image of 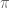 is always dense, and this seems to be enough for you (i.e., this still implies that the push-forward measure is translation-invariant). If
is always dense, and this seems to be enough for you (i.e., this still implies that the push-forward measure is translation-invariant). If  happens to be metrizable then
happens to be metrizable then 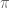 is surjective by countable saturation.
is surjective by countable saturation.
27 October, 2014 at 9:22 am
Terence Tao
Oh, thanks for pointing out that subtlety! I am so used to dealing with metrisable situations that I forgot that on non-metrisable spaces countable saturation is sometimes insufficient to guarantee closed images. But as you say, dense image is sufficient for the current application.
20 January, 2015 at 4:02 pm
Sean Eberhard
Correct me if I’m wrong but in fact I think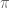 is *injective*. If we consider just the ultrafinite genuine group case for the moment, then there are lots of measurable characters on the ultraproduct coming from the ultraproduct of the dual groups: enough to separate points, by finite Fourier analysis. This implies that
is *injective*. If we consider just the ultrafinite genuine group case for the moment, then there are lots of measurable characters on the ultraproduct coming from the ultraproduct of the dual groups: enough to separate points, by finite Fourier analysis. This implies that 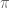 is injective.
is injective.
Somewhat related to this, I’m not sure I believe that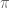 is (Loeb, Borel)-measurable. Though indeed the inverse images of the cylinder sets are measurable, unfortunately these do not generate the Borel sigma-algebra. I don’t have an example to prove this point though, so maybe I’ve just overlooked something. However I do beleive that
is (Loeb, Borel)-measurable. Though indeed the inverse images of the cylinder sets are measurable, unfortunately these do not generate the Borel sigma-algebra. I don’t have an example to prove this point though, so maybe I’ve just overlooked something. However I do beleive that 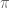 is (Loeb,Baire)-measurable, since by Stone-Weierstrass every continuous function on
is (Loeb,Baire)-measurable, since by Stone-Weierstrass every continuous function on  is the
is the  limit of a sequence of character sums.
limit of a sequence of character sums.
20 January, 2015 at 4:34 pm
Terence Tao
Yes, you’re right; I had forgotten about the distinctions between Baire and Borel in the inseparable case; I’ve updated the post to correct this. Regarding injectivity, I think you are right for the “universal” group T constructed in the blog post, but in practice one usually quotients down to a more manageable T (in particular, to a separable T, in order to avoid all these technical issues coming from inseparability), at which point injectivity is lost (but surjectivity is gained!). (But conclusion (iv) of the theorem need not hold for all functions f,g after such a quotienting; one can only save this conclusion for a separable space of functions, though this is usually plenty for applications.)
20 October, 2014 at 2:07 pm
Balazs Szegedy
I think that the following paper on mine (more recent than the one that you cite) is more relevant to this post:
http://arxiv.org/abs/1203.2260
In this paper I give a generalisation of the graph limit setting to the additive setting. I discuss how to take limits of subsets (or more generally functions) in compact abelian groups. Quite surprisingly the limit objects are defined on nil manifolds that are non-commutative structures.
Another very recent paper (joint with Lovasz) is about the non commutative setting:
http://arxiv.org/abs/1406.4958
Balazs
[Corrected, thanks – T.]
22 September, 2018 at 2:36 am
Group limits – Random Permutations
[…] few months ago on his blog Terry Tao explained how one could, by analogy with the theory of graph limits, replace the explicit […]
19 January, 2020 at 1:50 pm
The Kronecker factor of an ultrafinite group – Random Permutations
[…] few months ago on his blog Terry Tao explained how one could, by analogy with the theory of graph limits, replace the explicit […]