Analytic number theory is only one of many different approaches to number theory. Another important branch of the subject is algebraic number theory, which studies algebraic structures (e.g. groups, rings, and fields) of number-theoretic interest. With this perspective, the classical field of rationals , and the classical ring of integers
, are placed inside the much larger field
of algebraic numbers, and the much larger ring
of algebraic integers, respectively. Recall that an algebraic number is a root of a polynomial with integer coefficients, and an algebraic integer is a root of a monic polynomial with integer coefficients; thus for instance
is an algebraic integer (a root of
), while
is merely an algebraic number (a root of
). For the purposes of this post, we will adopt the concrete (but somewhat artificial) perspective of viewing algebraic numbers and integers as lying inside the complex numbers
, thus
. (From a modern algebraic perspective, it is better to think of
as existing as an abstract field separate from
, but which has a number of embeddings into
(as well as into other fields, such as the completed p-adics
), no one of which should be considered favoured over any other; cf. this mathOverflow post. But for the rudimentary algebraic number theory in this post, we will not need to work at this level of abstraction.) In particular, we identify the algebraic integer
with the complex number
for any natural number
.
Exercise 1 Show that the field of algebraic numbers
is indeed a field, and that the ring of algebraic integers
is indeed a ring, and is in fact an integral domain. Also, show that
, that is to say the ordinary integers are precisely the algebraic integers that are also rational. Because of this, we will sometimes refer to elements of
as rational integers.
In practice, the field is too big to conveniently work with directly, having infinite dimension (as a vector space) over
. Thus, algebraic number theory generally restricts attention to intermediate fields
between
and
, which are of finite dimension over
; that is to say, finite degree extensions of
. Such fields are known as algebraic number fields, or number fields for short. Apart from
itself, the simplest examples of such number fields are the quadratic fields, which have dimension exactly two over
.
Exercise 2 Show that if
is a rational number that is not a perfect square, then the field
generated by
and either of the square roots of
is a quadratic field. Conversely, show that all quadratic fields arise in this fashion. (Hint: show that every element of a quadratic field is a root of a quadratic polynomial over the rationals.)
The ring of algebraic integers is similarly too large to conveniently work with directly, so in algebraic number theory one usually works with the rings
of algebraic integers inside a given number field
. One can (and does) study this situation in great generality, but for the purposes of this post we shall restrict attention to a simple but illustrative special case, namely the quadratic fields with a certain type of negative discriminant. (The positive discriminant case will be briefly discussed in Remark 42 below.)
Exercise 3 Let
be a square-free natural number with
or
. Show that the ring
of algebraic integers in
is given by
If instead
is square-free with
, show that the ring
is instead given by
What happens if
is not square-free, or negative?
Remark 4 In the case
, it may naively appear more natural to work with the ring
, which is an index two subring of
. However, because this ring only captures some of the algebraic integers in
rather than all of them, the algebraic properties of these rings are somewhat worse than those of
(in particular, they generally fail to be Dedekind domains) and so are not convenient to work with in algebraic number theory.
We refer to fields of the form for natural square-free numbers
as quadratic fields of negative discriminant, and similarly refer to
as a ring of quadratic integers of negative discriminant. Quadratic fields and quadratic integers of positive discriminant are just as important to analytic number theory as their negative discriminant counterparts, but we will restrict attention to the latter here for simplicity of discussion.
Thus, for instance, when , the ring of integers in
is the ring of Gaussian integers
and when , the ring of integers in
is the ring of Eisenstein integers
where is a cube root of unity.
As these examples illustrate, the additive structure of a ring of quadratic integers is that of a two-dimensional lattice in
, which is isomorphic as an additive group to
. Thus, from an additive viewpoint, one can view quadratic integers as “two-dimensional” analogues of rational integers. From a multiplicative viewpoint, however, the quadratic integers (and more generally, integers in a number field) behave very similarly to the rational integers (as opposed to being some sort of “higher-dimensional” version of such integers). Indeed, a large part of basic algebraic number theory is devoted to treating the multiplicative theory of integers in number fields in a unified fashion, that naturally generalises the classical multiplicative theory of the rational integers.
For instance, every rational integer has an absolute value
, with the multiplicativity property
for
, and the positivity property
for all
. Among other things, the absolute value detects units:
if and only if
is a unit in
(that is to say, it is multiplicatively invertible in
). Similarly, in any ring of quadratic integers
with negative discriminant, we can assign a norm
to any quadratic integer
by the formula
where is the complex conjugate of
. (When working with other number fields than quadratic fields of negative discriminant, one instead defines
to be the product of all the Galois conjugates of
.) Thus for instance, when
one has
Analogously to the rational integers, we have the multiplicativity property for
and the positivity property
for
, and the units in
are precisely the elements of norm one.
Exercise 5 Establish the three claims of the previous paragraph. Conclude that the units (invertible elements) of
consist of the four elements
if
, the six elements
if
, and the two elements
if
.
For the rational integers, we of course have the fundamental theorem of arithmetic, which asserts that every non-zero rational integer can be uniquely factored (up to permutation and units) as the product of irreducible integers, that is to say non-zero, non-unit integers that cannot be factored into the product of integers of strictly smaller norm. As it turns out, the same claim is true for a few additional rings of quadratic integers, such as the Gaussian integers and Eisenstein integers, but fails in general; for instance, in the ring , we have the famous counterexample
that decomposes non-uniquely into the product of irreducibles in
. Nevertheless, it is an important fact that the fundamental theorem of arithmetic can be salvaged if one uses an “idealised” notion of a number in a ring of integers
, now known in modern language as an ideal of that ring. For instance, in
, the principal ideal
turns out to uniquely factor into the product of (non-principal) ideals
; see Exercise 27. We will review the basic theory of ideals in number fields (focusing primarily on quadratic fields of negative discriminant) below the fold.
The norm forms (1), (2) can be viewed as examples of positive definite quadratic forms over the integers, by which we mean a polynomial of the form
for some integer coefficients . One can declare two quadratic forms
to be equivalent if one can transform one to the other by an invertible linear transformation
, so that
. For example, the quadratic forms
and
are equivalent, as can be seen by using the invertible linear transformation
. Such equivalences correspond to the different choices of basis available when expressing a ring such as
(or an ideal thereof) additively as a copy of
.
There is an important and classical invariant of a quadratic form , namely the discriminant
, which will of course be familiar to most readers via the quadratic formula, which among other things tells us that a quadratic form will be positive definite precisely when its discriminant is negative. It is not difficult (particularly if one exploits the multiplicativity of the determinant of
matrices) to show that two equivalent quadratic forms have the same discriminant. Thus for instance any quadratic form equivalent to (1) has discriminant
, while any quadratic form equivalent to (2) has discriminant
. Thus we see that each ring
of quadratic integers is associated with a certain negative discriminant
, defined to equal
when
and
when
.
Exercise 6 (Geometric interpretation of discriminant) Let
be a quadratic form of negative discriminant
, and extend it to a real form
in the obvious fashion. Show that for any
, the set
is an ellipse of area
.
It is natural to ask the converse question: if two quadratic forms have the same discriminant, are they necessarily equivalent? For certain choices of discriminant, this is the case:
Exercise 7 Show that any quadratic form
of discriminant
is equivalent to the form
, and any quadratic form of discriminant
is equivalent to
. (Hint: use elementary transformations to try to make
as small as possible, to the point where one only has to check a finite number of cases; this argument is due to Legendre.) More generally, show that for any negative discriminant
, there are only finitely many quadratic forms of that discriminant up to equivalence (a result first established by Gauss).
Unfortunately, for most choices of discriminant, the converse question fails; for instance, the quadratic forms and
both have discriminant
, but are not equivalent (Exercise 38). This particular failure of equivalence turns out to be intimately related to the failure of unique factorisation in the ring
.
It turns out that there is a fundamental connection between quadratic fields, equivalence classes of quadratic forms of a given discriminant, and real Dirichlet characters, thus connecting the material discussed above with the last section of the previous set of notes. Here is a typical instance of this connection:
Proposition 8 Let
be the real non-principal Dirichlet character of modulus
, or more explicitly
is equal to
when
,
when
, and
when
.
- (i) For any natural number
, the number of Gaussian integers
with norm
is equal to
. Equivalently, the number of solutions to the equation
with
is
. (Here, as in the previous post, the symbol
denotes Dirichlet convolution.)
- (ii) For any natural number
, the number of Gaussian integers
that divide
(thus
for some
) is
.
We will prove this proposition later in these notes. We observe that as a special case of part (i) of this proposition, we recover the Fermat two-square theorem: an odd prime is expressible as the sum of two squares if and only if
. This proposition should also be compared with the fact, used crucially in the previous post to prove Dirichlet’s theorem, that
is non-negative for any
, and at least one when
is a square, for any quadratic character
.
As an illustration of the relevance of such connections to analytic number theory, let us now explicitly compute .
This particular identity is also known as the Leibniz formula.
Proof: For a large number , consider the quantity
of all the Gaussian integers of norm less than . On the one hand, this is the same as the number of lattice points of
in the disk
of radius
. Placing a unit square centred at each such lattice point, we obtain a region which differs from the disk by a region contained in an annulus of area
. As the area of the disk is
, we conclude the Gauss bound
On the other hand, by Proposition 8(i) (and removing the contribution), we see that
Now we use the Dirichlet hyperbola method to expand the right-hand side sum, first expressing
and then using the bounds ,
,
from the previous set of notes to conclude that
Comparing the two formulae for and sending
, we obtain the claim.
Exercise 10 Give an alternate proof of Corollary 9 that relies on obtaining asymptotics for the Dirichlet series
as
, rather than using the Dirichlet hyperbola method.
Exercise 11 Give a direct proof of Corollary 9 that does not use Proposition 8, instead using Taylor expansion of the complex logarithm
. (One can also use Taylor expansions of some other functions related to the complex logarithm here, such as the arctangent function.)
More generally, one can relate for a real Dirichlet character
with the number of inequivalent quadratic forms of a certain discriminant, via the famous class number formula; we will give a special case of this formula below the fold.
The material here is only a very rudimentary introduction to algebraic number theory, and is not essential to the rest of the course. A slightly expanded version of the material here, from the perspective of analytic number theory, may be found in Sections 5 and 6 of Davenport’s book. A more in-depth treatment of algebraic number theory may be found in a number of texts, e.g. Fröhlich and Taylor.
— 1. Ideals —
We begin by reviewing the notion of an ideal in an arbitrary commutative ring.
Definition 12 (Ideals) Let
be a commutative ring (in this set of notes, rings are understood to contain a multiplicative unit
). An ideal of
is an additive subgroup
of
with the property that
whenever
and
. Note that if
is an ideal, then the quotient
is well defined as a commutative ring. We write
for the quotient map from
to
, and write
if
, or equivalently if
is equal to
.
An ideal is proper if it is not all of. An ideal is principal if it is of the form
for some
, and non-zero if it is not the zero ideal
.
Ifare ideals, then the intersection
is an ideal, as is the sum
. The product set
need not be an ideal in general (it is not always closed under addition); however, we can define the product ideal
to be the ideal generated by this product set (that is, the intersection of all the ideals containing this product set). One can then define powers
for any
in the obvious fashion, with the convention that
. We say that
divides
if
, thus for instance
divides
for any ideals
. If
, we say that
strictly divides
.
An ideal is prime if it is proper, and it has the property that for anywith
, one has at least one of
or
true. Equivalently, an ideal
is prime if the quotient ring
is an integral domain.
One can easily check in the rational integers that product, divisibility, and primality correspond to their counterpart notions in the natural numbers. More precisely, if
are natural numbers, then
, that
divides
if and only if
divides
, and that
is prime if and only if
is prime. (But note that the zero ideal
is also prime, and can be viewed as a sort of “prime at infinity” from the perspective of scheme theory.) Also, if
is a natural number and
are integers, then
holds if and only if
. Thus we see that the above operations on ideals are quite compatible with their classical counterparts in
or
. Also, the integers form a principal ideal domain, in that every ideal
is principal; indeed, if
is non-zero, it is generated by the element of minimal norm. In particular, from the classical fundamental theorem of arithmetic we see that every non-zero ideal in
is uniquely factorisable (up to rearrangement) as the product of prime ideals.
Now we specialise to rings of quadratic integers, where
is a squarefree natural number. These more general rings
need no longer be principal ideal domains. For instance,
contains the non-principal ideal
. Closely related to this is the breakdown of the fundamental theorem of arithmetic for quadratic integers (i.e.
need not be a unique factorisation domain); for instance,
factors non-uniquely as
and
. Despite this, one still has unique factorisation at the level of ideals; for instance, in
it turns out that
factors uniquely as the product of
,
,
, and
. As we shall see, the precise failure of unique factorisation at the level of quadratic numbers can be quantified by an important number
, known as the class number of the ring of integers, where
is the discriminant mentioned in the introduction (equal to
when
, and
when
).
— 2. Unique factorisation of ideals —
Henceforth is a fixed squarefree natural number, and
is the ring of integers in
. We set the discriminant
equal to
when
and equal to
when
.
Exercise 13 (Algebraic interpretation of discriminant) Let
be an additive basis for
(thus
is generated by
as an additive group). Show that
We remark that the discriminant of a more general number field is defined similarly.
As mentioned in the introduction, one can view additively, as a rank two lattice in the complex numbers
. Any non-zero ideal
of
can then be seen to be a rank two sublattice of
, and in particular must have finite index. We refer to this index as the norm
of the ideal, thus
is the natural number defined by the formula
For the ring of quadratic integers we are considering here, one can interpret
geometrically as the area of the torus
, divided by the area of the torus
, which can be easily computed to be
.
It is clear that if divides
, then
divides
, since
is a quotient of
. Similarly, if
divides
and
, then one must have
. This implies the important Noetherian property:
does not contain any infinite strictly increasing sequence of ideals
since their norms must be strictly decreasing, creating an infinite descent which is absurd. This notion of norm is compatible with the notion of the norm of a quadratic integer:
Exercise 14 If
is a quadratic integer, show that
, where
was defined in the introduction.
We remark that for quadratic integers of positive discriminant the situation is slightly more complicated, because the norm of an individual element can now be negative, whereas the norm of an ideal is always positive. We will not dwell on this complication further here.
Now we develop a unique factorisation theory for ideals. We first establish that prime ideals are prime within the multiplicative structure of ideals (rather than of quadratic integers):
Lemma 15 Let
be a prime ideal that divides the product
of two ideals
. Then
must divide at least one of
.
Proof: If does not divide either of
, then we can find
that lie outside of
. As
is prime, we conclude that
also lies outside of
, and so
does not divide
, a contradiction.
Also, in a ring of quadratic integers, prime ideals are maximal:
Exercise 16 Show that the only ideals that divide a prime ideal
are
itself, and the full ring
.
If a non-zero ideal is not prime, then by definition there exist two quadratic integers
outside of
such that
. If we set
and
, we then see that
strictly divide
, and that
divides
. Thus any non-zero ideal
is either prime, or divides the product of two non-zero ideals that strictly divide it (and thus have smaller norm). Iterating this (and using the Noetherian property), we conclude
Proposition 17 Every non-zero ideal divides the product of a finite number of prime ideals.
A similar argument gives
Exercise 18 Show that every non-zero ideal is divisible by at least one prime ideal.
We now need a technical lemma that allows one to “invert” a prime ideal .
Lemma 19 Let
be a non-zero prime ideal. Then there exists a quadratic field element
that is not a quadratic integer (thus
), but is such that
.
Proof: Let be a non-zero element of
. By Proposition 17,
must divide some product
of prime ideals. In particular,
also divides
, which by Lemma 15 and Exercise 16 implies that one of the
, say
, is equal to
. By taking
to be minimal, we may assume that
does not divide
. Thus, we may find an element
of
that does not lie in
, but such that
is contained in
. Setting
, we obtain the claim.
Remark 20 We can formalise the notion of inverting an ideal by introducing the concept of a fractional ideal, which are to ideals as rational numbers are to integers, but we will not do so in this set of notes.
Now we can give the most difficult step of unique factorisation:
Proposition 21 Suppose
is a non-zero ideal that is divisible by a prime ideal
. Then one has
for some non-zero ideal
which is a strict divisor of
.
Proof: By the previous lemma, we can find that is not a quadratic integer, such that
. Note that
is an ideal dividing
, so by Exercise 16 is either equal to
or
.
Suppose first that . The ideal
is a rank two lattice, and thus isomorphic as an abelian group to
. The action of multiplication by
on
is then conjugate to the action of a
matrix with integer coefficients. By the Cayley-Hamilton theorem, this implies that there is a monic quadratic polynomial of
that annihilates
, and is thus zero (since
is an integral domain). In other words,
is an algebraic integer, and hence
, a contradiction. (Note here that we crucially used the fact that
contains all the algebraic integers of
; cf. Remark 4.)
Thus we must have . If we then set
, then we have
, and
is an ideal dividing
. We are thus done unless
, that is to say
. But one can then repeat the previous argument to conclude that
is an algebraic integer and thus in
, again reaching a contradiction.
We now have enough tools to mimic the usual proof of unique factorisation for natural numbers, to obtain the analogous result for ideals in a ring of quadratic integers:
Exercise 22 (Unique factorisation) Show that any non-zero ideal can be uniquely expressed (up to rearrangement) as a product
of non-zero prime ideals, with
. Show that one non-zero ideal
divides another
if and only if the number of times any given prime ideal
appears in the unique factorisation of
is less than or equal to the number of times it appears in
.
A basic application of unique factorisation is
Proposition 23 (Chinese Remainder Theorem) Let
be non-zero ideals that are coprime (they have no prime ideal divisors in common). Then the obvious ring homomorphism
from
to
, defined by setting
, is an isomorphism.
Proof: Observe that the ideal divides both
and
and must therefore be all of
, by unique factorisation and coprimality. Similarly, the ideal
is divisible by both
and
while dividing
, and must therefore be exactly
, by unique factorisation and coprimality. Since the kernel of
is
, we conclude that
is injective; it remains to show that
is surjective. Since
, we can split
for some
and
. But then
and
, and the surjectivity then follows since these two elements generate
as an
-module.
In the non-coprime case, we have the following basic fact.
Proposition 24 Let
be a non-zero prime ideal. Then for any non-negative integer
, we have
isomorphic (as a ring) to
.
Proof: By unique factorisation, is a strict divisor of
, thus we can find
that does not lie in
. This gives a ring homomorphism
defined by
. The kernel of this map is an ideal dividing
that does not contain
, and is thus
. Thus we have an injection from
to
.
It remains to show surjectivity. By several applications of Proposition 21, we may write for some non-zero ideal
not divisible by
. By the Chinese remainder theorem, we may then find, for any
, a quadratic integer
such that
and
. Thus
lies in both
and
, and hence in
by coprimality; thus
is a quadratic integer. By construction, we have
, giving the desired surjectivity.
Corollary 25 (Multiplicativity of norm) For any non-zero ideals
, we have
.
Proof: When are coprime this follows directly from the Chinese remainder theorem. By unique factorisation, it thus suffices to show that
for all natural numbers
. But this follows from Proposition 24 and induction on
.
Exercise 26 Show that the Gaussian integers and the Eisenstein integers are principal ideal domains. (Hint: if
is a non-zero ideal in one of these rings, consider a non-zero element of
of minimal norm.) Conclude a unique factorisation theorem for elements of these rings.
Exercise 27 Verify that in
, the principal ideal
factors into the four ideals mentioned in the introduction, and that these ideals are prime. What are the norms of all the ideals involved?
Remark 28 The unique factorisation theorem for ideals holds in the more general context of Dedekind domains, but we will not develop the abstract theory of Dedekind domains here.
— 3. Connection with the Kronecker symbol —
Let be a prime ideal, then
is a finite integral domain, and is thus a finite field (each non-zero element acts via multiplication by a permutation). On the other hand, since
is a rank two abelian group, this finite field must have rank at most two. We conclude that
is isomorphic to a finite field of order either
or
for some rational prime
, which is the characteristic of the field. In particular,
is either a prime
or a square
of that prime
. On the other hand, since
has characteristic
,
must divide
, which has norm exactly
by Exercise 14. By unique factorisation, we conclude that for each rational prime
, the ideal
is either prime of norm
, or is the product
of two prime ideals that each have norm
, and furthermore that all prime ideals arise in this fashion.
We can determine precisely which of the two is the case:
Proposition 29 Let
be a rational prime.
- If
is a quadratic residue modulo
, then
is the product of two prime ideals
of norm
.
is a quadratic non-residue modulo
, then
is a prime ideal of norm
.
Proof: We just handle the case and leave the
case as an exercise. Suppose there is an prime ideal
of norm
, then
is isomorphic to the field of order
. In particular, if
is a element of
not divisible by
, then
must be a multiple of
modulo
, thus one can find non-zero
such that
and
, which implies that
, since
are not both zero modulo
. Thus
(and hence
) is a quadratic residue modulo
. Conversely, if
(and hence
) is a quadratic residue, then we can find
with
and
with
not both zero modulo
, and then
is an ideal dividing
of norm
, and thus prime. The claim follows.
Exercise 30 Complete the proof of the proposition in the case
.
Exercise 31 Show that when
is a quadratic residue modulo
, the two prime ideals
appearing in the above proposition are distinct unless
divides
, in which case the two ideals are equal.
The above proposition gives us a formula for the number of prime ideals of a given norm. For any natural number , define the Kronecker symbol
to be the completely multiplicative function of
such that for each prime
,
equals
if
divides
, equals
if
is a non-zero quadratic residue mod
, and
if
is a non-zero quadratic nonresidue mod
. From the law of quadratic reciprocity, one can verify that
is a Dirichlet character of conductor
. For instance, if
,
.
Exercise 32 Show that for any natural number
, the number of ideals of norm
is equal to
.
Exercise 33 Prove Proposition 8.
Another way to phrase the conclusion of Exercise 32 is as the factorisation
(for at least), where
is the Riemann zeta function,
is the Dedekind zeta function
where ranges over prime ideals, and
is the Dirichlet
-function
For instance, in the case of the Gaussian integers , we have
— 4. Connection with quadratic forms —
Let us say that two ideals are equivalent if one has
for some
. This is clearly an equivalence relation; the equivalence class of
is simply the class of principal ideals. Using unique factorisation (and the fact that every ideal divides a principal ideal), the space of such equivalence classes is a group, called the class group of the ring of integers
.
One can analyse this class group by associating a positive definite quadratic form to each ideal
, by the formula
for all . Note that
for
, and so
takes values in the non-negative integers (and is strictly positive for non-zero
). Since
is a quadratic form in
, we see that
is a quadratic form on
.
We call two quadratic forms ,
equivalent if there is an additive group isomorphism
such that
for all
. This relation captures the equivalence relation on ideals:
Exercise 34 Let
be ideals. Show that
and
are equivalent if and only if
are equivalent.
A quadratic form on the standard lattice
is of the form
for some integers
. The discriminant of this quadratic form is defined to be
. This is an invariant with respect to invertible linear transformations of
. Thus, given any other quadratic form
on a rank two lattice
, one can define the discriminant of
by identifying
with
via a linear isomorphism; it is clear that this definition does not depend on the choice of isomorphism. It turns out that the quadratic form of all ideals have the same discriminant:
Exercise 35 Let
be an ideal. Show that
has discriminant
. (Hint: if one identifies
with
, show that
takes the form
for some linear transformation
of determinant
, and use this to show that
has the same discriminant as
.)
From Exercise 7 we see that the class group of is finite. The order of this group is known as the class number and will be denoted
.
In the converse direction, we have
Lemma 36 Let
be a positive definite quadratic form of discriminant
. Then there exists an ideal
such that
is equivalent to
.
In particular, the class group is in one-to-one correspondence with the equivalence classes of positive definite quadratic forms of a given discriminant, a famous result of Gauss. In particular, the group law on the class group induces the Gauss composition law on equivalence classes of quadratic forms of a given discriminant.
Proof: We perform some ad hoc computations in the case . If
, then
and
, which makes
even. One may verify that the set
is an additive subgroup of that is also closed under multiplication by
, and is thus an ideal; one may also calculate its norm to be
, with
for . This implies that
is equivalent to
as required.
Exercise 37 Complete the proof of the lemma by treating the
case.
Exercise 38 Show that
and
are inequivalent quadratic forms of discriminant
, and that all other quadratic forms of this discriminant are equivalent to one of these two forms.
Now we relate the distribution of norms of ideals to representation by quadratic forms.
Proposition 39 Let
be a natural number, and let
be representatives of the equivalence classes of positive definite quadratic forms of discriminant
. Then the number of ideals
with
is equal to the number of representations of
of the form
for some
and
, divided by the number
of units (i.e.
if
,
if
, or
otherwise, thanks to Exercise 5).
Proof: Suppose we can write for some
and
. By construction,
is isomorphic to
for some ideal
, and so we can write
for some
, thus
. By unique factorisation, we may write
for some ideal
of norm
. Note that if we replace
with a different index, then
is replaced with an inequivalent ideal, and then so is
. On the other hand, if we keep
fixed and replace
with some
, thus also replacing
with some
, then we also change
to a different ideal unless
, or equivalently if
differs from
by a unit, in which case
is unchanged. Thus we have a map from representations
with
and
to ideals of norm
whose multiplicity is exactly equal to the number
of units.
To conclude the proposition, we need to show that every ideal of norm
arises in this fashion. But by Lagrange’s theorem,
lies in
, and then
, giving the claim.
We can then give an elementary asymptotic for the norm of ideals:
Corollary 40 We have
for
, where
is the number of units.
Proof: By the preceding proposition, the left-hand side can be written as
The inner sum is the number of lattice points in the ellipse , which has area
by Exercise 6, since
has discriminant
. If one places a unit square centred at each such lattice point, one obtains a region that differs from the ellipse by a set of area
(since the difference set is contained in a
-neighbourhood of the boundary of the ellipse). The claim follows.
This, combined with Exercise 32, gives a special case of the famous Dirichlet class number formula, generalising Exercise 9:
Exercise 41 (Dirichlet class number formula) Show that
for
sufficiently close to
, and then conclude that
In particular, since the class number is clearly at least one, we obtain a “trivial” lower bound
This looks weaker than Siegel’s bound
for any (which we will discuss in later notes), but a key difference is that the trivial bound has effective constants, whereas Siegel’s bound is ineffective. The best effective bound currently known on
only improves on the trivial bound by a logarithmic factor, and involves quite deep and difficult mathematics relating to elliptic curves; see this survey of Goldfeld.
Remark 42 Most of the above discussion also extends to the rings of integers in real quadratic fields
of positive discriminant, with a few changes; for instance, there are now infinitely many units, quadratic integers may now have negative norm, and the field is now embedded (in two different ways) into
rather than into
. The ellipses of Exercise 6 become hyperbolae, which creates a logarithmic correction term (known as a regulator) in the class number formula. We leave the detailed modifications needed to the interested reader. It turns out that every real Dirichlet character will essentially arise from a quadratic field (of either positive or negative discriminant); see Chapters 5, 6 of Davenport for details. One can also consider higher degree number fields than quadratic fields; again, much of the above theory carries through in this case, but the characters
that then emerge are not necessarily Dirichlet characters, but lie instead in the more general class of Hecke characters. We will not discuss this more general theory here, but see for instance the book of Fröhlich and Taylor.
Remark 43 There is an important connection between class groups and abelian extensions of fields (an abelian version of the connection between Galois groups and arbitrary extensions of fields), known as class field theory, but we will not discuss this topic further in this course.
Exercise 44 Let
be a rational prime with
, thus generating a quadratic field
of discriminant
and the associated ring of integers
.
- (i) Show that for any rational integer
with
, that the only solutions to the equation
are
.
- (ii) Suppose further that the class number
is
, that is to say that
is a principal ideal domain. Conclude that
is prime for all rational integers
. (The converse statement is also true, a result of Rabinovitch.) For instance, the discriminant
is known to have class number one, giving Euler’s famous prime-generating polynomial
, which gives primes for
, as well as Legendre’s variant
, which gives primes for
. (This also generates some of the lines in Ulam’s spiral.) Unfortunately,
is the largest value of
with this property, thanks to the Stark-Heegner theorem.

21 comments
Comments feed for this article
29 November, 2014 at 8:07 am
tomcircle
Reblogged this on Math Online Tom Circle.
29 November, 2014 at 4:32 pm
Anonymous
The algebraic numbers don’t embed into the p-adics.
[Corrected, thanks – T.]
4 December, 2014 at 4:17 am
MrCactu5 (@MonsieurCactus)
If I recall, – isomorphic as fields, but not as normed spaces. This always confused me. http://ncatlab.org/nlab/show/p-adic+complex+number http://math.stackexchange.com/questions/338148/is-there-an-explicit-embedding-from-the-various-fields-of-p-adic-numbers-mathb
– isomorphic as fields, but not as normed spaces. This always confused me. http://ncatlab.org/nlab/show/p-adic+complex+number http://math.stackexchange.com/questions/338148/is-there-an-explicit-embedding-from-the-various-fields-of-p-adic-numbers-mathb
1 December, 2014 at 12:01 am
eigenlambda
prime ideals are only proper in rings of low dimension
1 December, 2014 at 12:05 am
eigenlambda
derp principal sorry :(
3 December, 2014 at 1:45 pm
anthonyquas
I think the area in Exercise 5 is out by a factor of 2.
[It looks alright to me – e.g. if and
and 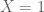 , then
, then  and the area is
and the area is 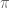 . -T.]
. -T.]
3 December, 2014 at 2:56 pm
anthonyquas
Oops.
3 December, 2014 at 3:01 pm
anthonyquas
So now I’m doubting myself, but I’m having a hard time following the calculations after the use of the Dirichlet hyperbola method in the proof of Corollary 2. It looks as though the second and third terms are . I don’t see why the first term is
. I don’t see why the first term is 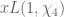 though.
though.
[Oops, there was a typo in one of the estimates needed to justify this first term; should be
should be 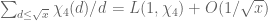 . Hopefully this resolves the issue – T.]
. Hopefully this resolves the issue – T.]
3 December, 2014 at 3:04 pm
anthonyquas
In Exercise 7, the summation is over , not
, not ![\mathbf Z[\sqrt{-1}]](https://s0.wp.com/latex.php?latex=%5Cmathbf+Z%5B%5Csqrt%7B-1%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) , right?
, right?
[Corrected, thanks – T.]
3 December, 2014 at 6:26 pm
anthonyquas
When defining the product of two ideals, the issue is that they may not be closed under addition (not multiplication) isn’t it?
[Corrected, thanks – T.]
4 December, 2014 at 3:41 pm
MeromorphicFunction
Is there a straightforward explanation, in your view, to classify whether a number theoretic question would be amenable to analytic techniques, or where algebraic theory would be a better approach?
It is ‘obvious’ that Sato-Tate belongs in the realm of algebraic number theory whilst issues of gaps between primes fall into the analytic landscape, but I can’t express why in words.
4 December, 2014 at 5:35 pm
Terence Tao
A good question! Broadly, I’d say that algebraic techniques are strongest when there is a lot of algebraic structure present in the problem, and analytic techniques are strongest when there is a lot of exploitable “mixing” (e.g. Dirichlet convolutions or additive convolutions, or (preferably) both). For instance, when trying to count representations as the sum of two squares, one should definitely use the algebraic structure of the Gaussian integers, but when trying to count representations as the sum of five or more squares, there is so much additive convolution going on that analytic methods become much more effective. (Four squares is an interesting borderline case in which one needs a mix of methods to get good results.)
In a separate direction, analytic methods tend to be best at finding solutions to equations in which we expect to have quite a large number of solutions (e.g. the expected number of solutions of height up to X is some power of X). Such methods are much worse at finding solutions when the solution set is expected to be very sparse (e.g. logarithmic in the height), or to show that there are no solutions at all (although they can sometimes be used to show that the existence of one solution repels other solutions, giving a finiteness theorem on the number of solutions without an effective bound on heights). For instance, I see no plausible path to using analytic methods to prove Fermat’s last theorem, though perhaps one could use those methods to prove enough of Faltings’ theorem (say) to show that the number of solutions for a fixed exponent is finite.
13 January, 2015 at 8:02 pm
Anonymous
A is much larger buts its inside Q…?
13 January, 2015 at 8:21 pm
Anonymous
+1…larger than the other Q, got it, plus one for being an idiot
22 January, 2015 at 4:14 pm
Martin Hughes
Has anyone ever tried to use wave theory to understand prime numbers? If you list all the numbers not excluded from being prime by 2 & 3 – i.e 6n-1 numbers in one column and 6n+1 numbers in the other – you get zigzag lines that could be thought of as waves between the columns.
The relation between the rows in these columns and the number is really neat. 5 has frequency of 5 rows and the wave is made up of a 3 down and then a 2. 7 has a 5 down then a 2. the waves – expressed as rows down – always relate to the numbers and so too to the combinations. The combined wave of 5 & 7 has a frequency. all the frequencies over 5 & 7 have a frequency defined in terms of 6n+-1 numbers.
There are many other patterns such as the two potential twin primes on each row share the same even number in their wave frequency. Each successive number has the previous one as its other wave part. we don’t need to sieve out the numbers that get hit by these waves since they don’t affect the pattern.
We just have to decide when we want to know if a particular number is prime and see what the wave theory tells us. numbers with lots of divisors show up as higher than those with less. primes will always have the same hight to their wave, their square will always have twice the height, and cubes three quarter the height. They look just like waves so why not treat them as such? I am not a maths wiz so I imagine that there is some reason why this is a ridiculous suggestion.
22 January, 2015 at 4:42 pm
Terence Tao
In a sense, yes: the main mathematical tool to analyse waves is Fourier analysis, which is also one of the major tools used to analyse the prime numbers, in effect treating the prime numbers (or proxies for the prime numbers, such as the von Mangoldt function) as a wave. This Fourier analysis can be done with respect to additive spacings between primes (leading to the Hardy-Littlewood circle method, which does indeed capture such phenomena as the primes being mostly supported on the numbers ) or multiplicative spacings between primes (leading to the theory of the Riemann zeta function). The latter is sometimes referred to as the “music of the primes”, which again invokes a wave analogy (sound waves, in this case); for instance, the zeroes of the Riemann zeta function can be thought of as the “notes” in the “music” that the primes comprise (the mathematical formalisation of this statement is known as the explicit formula).
) or multiplicative spacings between primes (leading to the theory of the Riemann zeta function). The latter is sometimes referred to as the “music of the primes”, which again invokes a wave analogy (sound waves, in this case); for instance, the zeroes of the Riemann zeta function can be thought of as the “notes” in the “music” that the primes comprise (the mathematical formalisation of this statement is known as the explicit formula).
However, a major problem with either of these approaches to prime number theory is that they have difficulty handling the “noisy” part of the wave – in the additive approach this contribution is known as the “minor arc” contribution, and in the multiplicative approach this corresponds to the contribution of the bulk of the non-trivial zeroes of the zeta function. This noise also obscures what is going on in the late stages of sieving processes such as the sieve of Eratosthenes; we understand pretty well what happens when we sieve out multiples of (say) 2, 3, 5 from the natural numbers up to when trying to isolate (say) twin primes, but the process of sieving out the multiples between, say,
when trying to isolate (say) twin primes, but the process of sieving out the multiples between, say, 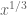 and
and  is much less well understood. One can make some pseudorandomness hypotheses about this “noise” which leads to predictions in analytic theory that look quite convincing (for instance giving asymptotics for the density of twin primes that agrees very well with numerics), but unfortunately fall short of a rigorous argument.
is much less well understood. One can make some pseudorandomness hypotheses about this “noise” which leads to predictions in analytic theory that look quite convincing (for instance giving asymptotics for the density of twin primes that agrees very well with numerics), but unfortunately fall short of a rigorous argument.
15 August, 2015 at 10:51 pm
A wave equation approach to automorphic forms in analytic number theory | What's new
[…] one (this fact is equivalent to the unique factorisation of the gaussian integers, as discussed in this previous post), every form in this space is equivalent (under the action of some element of ) with the standard […]
5 June, 2019 at 7:42 pm
Fermat Primes and the Gauss-Wantzel Theorem - AMSI Vacation Research Scholarships 2018/19
[…] https://terrytao.wordpress.com/2014/11/28/245a-supplement-1-a-little-bit-of-algebraic-number-theory-… […]
1 November, 2020 at 9:22 pm
Xiang Yu
Line 2 of the proof of Proposition 21: It states that “Noting that is an ideal dividing
is an ideal dividing 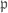 “. I do not understand how can we conclude this from the previous lemma. In Lemma 19,
“. I do not understand how can we conclude this from the previous lemma. In Lemma 19,  is defined as
is defined as  , so
, so  dividing
dividing 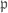 means that
means that  , which seems not obvious in the proof of Lemma 19. Could you explain a little bit more on the problem? Thanks
, which seems not obvious in the proof of Lemma 19. Could you explain a little bit more on the problem? Thanks
Line 7 of the proof of Proposition 24: There might be a typo. I think it should be “quadratic integer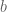 such that
such that 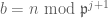 “.
“.
[Corrected, thanks. One should have worked with rather than
rather than  . -T]
. -T]
12 June, 2021 at 1:15 am
Sean Prendiville
Thanks for another great introduction!
Regarding §2 (Unique factorisation of ideals):
In this section, it would be good to caveat which results are specific to the particular rings in which we are working. For example, Exercise 16 is specific to the context (not all non-zero prime ideals are maximal in general commutative rings), whilst the preamble before Lemma 15 emphasises that this result holds in general. As written, it is not clear which facts hold in general commutative rings, and this could be confusing for a beginner (at least it was for me!).
Additional pedantic comment: some of the results of §2 require the prime ideal to be non-zero.
[Post updated to incorporate suggestions, thanks – T.]
11 October, 2021 at 9:19 am
254A, Supplement 4: Probabilistic models and heuristics for the primes (optional) | What's new
[…] to various finite groups of number-theoretic importance, such as the class groups discussed in Supplement 1, there are also heuristics of Cohen-Lenstra type. Historically, the first heuristic discussion of […]