The Polymath14 online collaboration has uploaded to the arXiv its paper “Homogeneous length functions on groups“, submitted to Algebra & Number Theory. The paper completely classifies homogeneous length functions 
on an arbitrary group 
, that is to say non-negative functions that obey the symmetry condition 
, the non-degeneracy condition 
, the triangle inequality 
, and the homogeneity condition 
. It turns out that these norms can only arise from pulling back the norm of a Banach space by an isometric embedding of the group. Among other things, this shows that 
can only support a homogeneous length function if and only if it is abelian and torsion free, thus giving a metric description of this property.
The proof is based on repeated use of the homogeneous length function axioms, combined with elementary identities of commutators, to obtain increasingly good bounds on quantities such as ![{\|[x,y]\|}](https://s0.wp.com/latex.php?latex=%7B%5C%7C%5Bx%2Cy%5D%5C%7C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
, until one can show that such norms have to vanish. See the previous post for a full proof. The result is robust in that it allows for some loss in the triangle inequality and homogeneity condition, allowing for some new results on “quasinorms” on groups that relate to quasihomomorphisms.
As there are now a large number of comments on the previous post on this project, this post will also serve as the new thread for any final discussion of this project as it winds down.
What's new 
17 comments
Comments feed for this article
11 January, 2018 at 9:06 pm
Terence Tao
I’ve also submitted the paper to Algebra & Number Theory. Thanks to everyone for their participation in what I found to be an enjoyable and productive project!
12 January, 2018 at 2:33 am
Tobias Fritz
I also want to say thanks to everyone! It has been a lot of fun and also a great learning experience.
I feel like our problem has been just about right for such a project: not too hard and not too easy, simple to grasp, and approachable from a lot of different angles. Especially concerning the level of difficulty, this problem was more rewarding than Polymath11 on the union-closed sets conjecture, where we had run out of steam after two months. I’m looking forward to possible future Polymath projects, whether that may be as a participant or as a curious spectator.
25 March, 2018 at 3:47 pm
Roy Abrams
Tobias, apologies for the late follow up, but in regards to Polymath 11, how does this idea sound?
1. Frankl’s Conjecture asserts that in any family of sets (1,2,3…) that is union closed, there is a least one element (a,b,c…) found in at least half of all the subsets of the set containing all elements in the family.
2. Arrange the sets in ascending order of cardinality, from smallest set to the set containing all elements. Sets of equal cardinality can be put in any order within the overall arrangement.
3. The smallest set is “irreducible.” The union of any two sets is either a subset of the larger one, or has cardinality greater than the larger one, or is, in the case of two sets of equal cardinality, a set of greater cardinality.
4. Number the sets from 1 to N in ascending order, N being the set of greatest cardinality.
5. Create the power set of all sets, 1 to N – 1.
6. Because set union is associative and commutative, and because union-closed families include every union, every set represented in the power set is a member of the union closed family, one of the numbered sets used as generators.
7. Some of these sets are entirely contained in their set of greatest cardinality. Some include all the sets enumerated, but belong to a set of greater cardinality that is not part of the bracketed sets.
8. Because the number of subsets of the power set is strictly larger that the set containing the original elements (and grows exponentially), each element will be represented by multiple subsets of the power set.
9. Therefore multiple subsets will be equivalent, representing the same unique generating set.
10. Equivalence of these subsets of the original set implies intersections, i.e., element(s) (a,b,c…) appear in more than one generating set.
11. Using the ‘irreducibility” of the least set (1), you should be able to establish a chain of subsets in which one is included in more than half the original sets (1,2,3…). Obviously, the power set grows must faster than the number of original sets, so a kind of induction might be possible.
12. For example, establish that 1 is a proper subset of 3, establish that 3 is a proper subset of 6, etc.
26 March, 2018 at 3:29 am
Tobias Fritz
I can follow your reasoning up to item 10, but the main problem is how to prove a statement along the lines of your item 11. One issue is that a set of least cardinality does not necessarily have abundance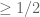
; in fact, it’s easy to construct examples showing that its abundance can be arbitrarily small, even when it’s the unique set of least cardinality.
My general feeling at the end of Polymath11 has been that we had just scratched the surface of the problem, getting some feel for how difficult it is. The naive hope that I had at the end is that it may be possible to derive a constant lower bound (but smaller than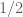
) by proving a suitable result on approximating every finite lattice by another type of lattice for which FUNC is known to hold, e.g. a geometric lattice. This goes in a vaguely similar direction as what you’re suggesting. But I don’t know how to go about this technically, and it will definitely require an enormous effort.
In any case, perhaps this discussion would be more appropriate over at the last Polymath11 thread?
26 March, 2018 at 7:01 am
Roy Abrams
Thanks, Tobias.
12 January, 2018 at 2:34 am
Anonymous
It seems that the numbering of results is not consecutive (e.g. results 1.1 and 1.2 are missing).
12 January, 2018 at 2:40 am
Tobias Fritz
We seem to be using an enumeration style where equations and theorem environments have a shared counter. So (1.1) and (1.3) are equations, and similarly in Section 2.
12 January, 2018 at 5:14 am
Siddhartha Gadgil
Thanks to everyone from me too. It was truly enjoyable and I learnt a lot.
Mainly as an exercise for my benefit. I have formalized (in the sense of computer verified, but with idiosyncratic foundations) the internal repetition lemma at http://siddhartha-gadgil.github.io/ProvingGround/tuts/LengthFunctions.html
13 January, 2018 at 4:58 pm
nicodean
Terence Tao wrote on 22.Dec 2017: “Secondly, again as with some previous Polymath projects, computer assistance was quite important, even if the final proof is not visibly computer-assisted in any way. […]. We’re still some way off from the dream of computers routinely generating large chunks of proofs and/or conjectures for us, but nevertheless they are playing an increasingly essential role in mathematics.”
Is there any possibility to summarize in more details of computer-assistance (by any of the participants; and on a more abstract level maybe, i am not an expert in this field)? Also maybe in the other polymath projects? Is there a structure of mathematical problems that are quite good for computer-assisted proofs? What where the insights, has it “just” been the calculation of difficult formulars – i.e. standard Mathematica problems? This is super interesting!
13 January, 2018 at 7:09 pm
Siddhartha Gadgil
The role of the computer (used by me) was to find a proof of an (at that time best) concrete bound on the length of the commutator of generators, and output this in a (barely) human readable form as [posted](https://github.com/siddhartha-gadgil/Superficial/wiki/A-commutator-bound). Pace Nielsen read through the proof and saw a pattern, with the “same” conjugacy and the “same” pair of triangle inequalities being repeatedly applied in this proof. This was used by him to get strong bounds, and then he and others refined and abstracted this to get the _splitting lemma_ in the paper.
There were two limitations of the way the computer proof was done:
* While the use of conjugacy invariance and triangle inequality was optimal and algorithmic, of which elements to take powers was manually specified by me. This should have been made smart, and would have soon enough except the extreme smartness of the people in this polymath group made this redundant (problem was solved within 24 hours of the first posted computer proof).
* More importantly, I used [domain specific foundations](https://github.com/siddhartha-gadgil/Superficial/blob/master/src/main/scala/freegroups/LinNormBound.scala), which could encode only one kind of proof, that a specific word has length bounded by a specific number. This rules out in particular both firmulas for bounds that are quatified (and so must invlove variables) and recursion/induction. To show that such results can be at least _encoded_ I formalized the [internal repetition trick](http://siddhartha-gadgil.github.io/ProvingGround/tuts/LengthFunctions.html).
More generally, where a computer helped was in following instructions of the form “try these method in lots of cases in lots of ways and give me the best proof for thess cases (or where we got a strong result)”. It is obvious that the “lots of cases” and “lots of ways” are much bigger numbers for computers than by hand. The question is how general one can be with “these methods”. I do think even in practice a lot of methods can be encoded, and this is underutilized as people underestimate this. In principle, in the era of Homotopy type theory and Deep learning, presumably every method can be encoded.
16 January, 2018 at 4:49 am
J Button
Hi – didn’t see the blog until the arxiv paper was posted and now
this feels rather late in the day (or sometime the next day) but
still: why can’t we argue thus….
Given
with homogeneous (pseudo-) length function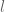 
,
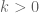be your favourite upper bound that holds for all![l([a,b])\leq k](https://s0.wp.com/latex.php?latex=l%28%5Ba%2Cb%5D%29%5Cleq+k&bg=ffffff&fg=545454&s=0&c=20201002)
for all 
. By![[a,b]^3=[aba^{-1},b^{-1}aba^{-2}][b^{-1}ab,b^2]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%5E3%3D%5Baba%5E%7B-1%7D%2Cb%5E%7B-1%7Daba%5E%7B-2%7D%5D%5Bb%5E%7B-1%7Dab%2Cb%5E2%5D&bg=ffffff&fg=545454&s=0&c=20201002)
![3l([a,b])\leq l([aba^{-1},b^{-1}aba^{-2}])+l([b^{-1}ab,b^2]) \leq 2k](https://s0.wp.com/latex.php?latex=3l%28%5Ba%2Cb%5D%29%5Cleq++l%28%5Baba%5E%7B-1%7D%2Cb%5E%7B-1%7Daba%5E%7B-2%7D%5D%29%2Bl%28%5Bb%5E%7B-1%7Dab%2Cb%5E2%5D%29+%5Cleq+2k&bg=ffffff&fg=545454&s=0&c=20201002)
, thus we now know ![l([a,b])\leq 2k/3](https://s0.wp.com/latex.php?latex=l%28%5Ba%2Cb%5D%29%5Cleq+2k%2F3&bg=ffffff&fg=545454&s=0&c=20201002)
holds for any
![l([a,b])\leq k(2/3)^n](https://s0.wp.com/latex.php?latex=l%28%5Ba%2Cb%5D%29%5Cleq+k%282%2F3%29%5En&bg=ffffff&fg=545454&s=0&c=20201002)
for all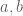 
and hence ![l([a,b])=0](https://s0.wp.com/latex.php?latex=l%28%5Ba%2Cb%5D%29%3D0&bg=ffffff&fg=545454&s=0&c=20201002)
.
let
commutators, thus
Culler’s identity
(sometimes seen in introductions to stable commutator length)
we have
commutator. So now use the argument recursively to get
16 January, 2018 at 5:05 am
Tobias Fritz
That’s a nice idea, but it doesn’t quite work like that: in any nonzero upper bound, the right-hand side also should be linear in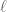
, e.g. of the form ![\ell([a.b])\leq k(\ell(a) + \ell(b))](https://s0.wp.com/latex.php?latex=%5Cell%28%5Ba.b%5D%29%5Cleq+k%28%5Cell%28a%29+%2B+%5Cell%28b%29%29&bg=ffffff&fg=545454&s=0&c=20201002)
. Using conjugation invariance, we can deduce from Culler’s identity that
assuming that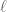
satisfies homogeneity and the triangle inequality on the nose. Thus ![\ell([a,b]) \leq k(\tfrac{2}{3}a + \tfrac{5}{3}b)](https://s0.wp.com/latex.php?latex=%5Cell%28%5Ba%2Cb%5D%29+%5Cleq+k%28%5Ctfrac%7B2%7D%7B3%7Da+%2B+%5Ctfrac%7B5%7D%7B3%7Db%29&bg=ffffff&fg=545454&s=0&c=20201002)
.
Doing a more refined analysis along the lines of Proposition 1 in the second blog post could be interesting, but I haven’t done this yet and find it hard to say whether it would have the potential to lead to an alternative proof or not.
16 January, 2018 at 8:26 am
J Button
Ah, yes – thanks! We don’t have a uniform upper bound for commutators (was going between a,b for free basis and for
arbitrary elements).
16 January, 2018 at 11:13 am
Lior Silberman
This is to record an erratum pointed out to us by email and its correction.
Let
be a group equipped with a homogeneous norm 
(
is necessarily abelian and torsion-free). Then this norm extends to a norm on the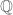 
-vectorspace 
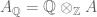. In detail, every element of 
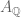has a representative of the form 
with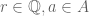 
and we set 
.
Now let $\overline{A_\mathbb{Q}}$ be the metric completion of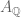
. This is still a normed group into which 
embeds, and is in fact an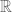 
-vectorspace: if 
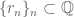and 
are Cauchy sequences and then so is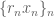 
and it is easy to check that its equivalence class depends only on the equivalence classes on the original sequences. Since also 
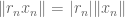it also follows that the norm is 
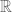-homogenous. In summary, 
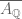is naturally a complete normed 
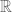-vector space, that is a Banach space.
Finally, there is a natural map of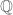
-vectorspaces 
. This map is injective since our extension of the norm was still a norm. Since the RHS is compatibly an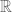 
-vectorspace, this induces a further map of 
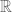-vectorspaces
However, the latter map need not be injective! In other words, when we pull back the norm from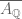
to 
, the result need only be a seminorm.
For example, if we start with the norm
on 
then the same formula defines a norm on 
but only a seminorm on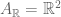 
. To get a norm we need to divide by the subspace 
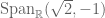which is compatible with everything we’ve said since this subspace is disjoint from the image of 
here so 
and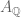 
still inject in the quotient (isometrically, as they must).
16 January, 2018 at 12:04 pm
Lior Silberman
Adding: this is all already in the paper; but we could clarify better the distinction between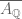
(in the paper called 
) and 
).
25 January, 2018 at 10:28 pm
Spontaneous Polymath 14 – A success! | The polymath blog
[…] This post is to report an unplanned polymath project, now called polymath 14 that took place over Terry Tao’s blog. A problem was posed by Apoorva Khare was presented and discussed and openly and collectively solved. (And the paper arxived.) […]
1 October, 2020 at 7:36 am
Terence Tao
Readers who had followed the Polymath14 project may be interested to know that the discussion for this project was used as a test data set for a collaborative research platform “Sophize”, as presented in this video.