I have just uploaded to the arXiv my paper “On the universality of the incompressible Euler equation on compact manifolds, II. Non-rigidity of Euler flows“, submitted to Pure and Applied Functional Analysis. This paper continues my attempts to establish “universality” properties of the Euler equations on Riemannian manifolds , as I conjecture that the freedom to set the metric
ought to allow one to “program” such Euler flows to exhibit a wide range of behaviour, and in particular to achieve finite time blowup (if the dimension is sufficiently large, at least).
In coordinates, the Euler equations read
where is the pressure field and
is the velocity field, and
denotes the Levi-Civita connection with the usual Penrose abstract index notation conventions; we restrict attention here to the case where
are smooth and
is compact, smooth, orientable, connected, and without boundary. Let’s call
an Euler flow on
(for the time interval
) if it solves the above system of equations for some pressure
, and an incompressible flow if it just obeys the divergence-free relation
. Thus every Euler flow is an incompressible flow, but the converse is certainly not true; for instance the various conservation laws of the Euler equation, such as conservation of energy, will already block most incompressible flows from being an Euler flow, or even being approximated in a reasonably strong topology by such Euler flows.
However, one can ask if an incompressible flow can be extended to an Euler flow by adding some additional dimensions to . In my paper, I formalise this by considering warped products
of
which (as a smooth manifold) are products
of
with a torus, with a metric
given by
for , where
are the coordinates of the torus
, and
are smooth positive coefficients for
; in order to preserve the incompressibility condition, we also require the volume preservation property
though in practice we can quickly dispose of this condition by adding one further “dummy” dimension to the torus . We say that an incompressible flow
is extendible to an Euler flow if there exists a warped product
extending
, and an Euler flow
on
of the form
for some “swirl” fields . The situation here is motivated by the familiar situation of studying axisymmetric Euler flows
on
, which in cylindrical coordinates take the form
The base component
of this flow is then a flow on the two-dimensional plane which is not quite incompressible (due to the failure of the volume preservation condition (2) in this case) but still satisfies a system of equations (coupled with a passive scalar field
that is basically the square of the swirl
) that is reminiscent of the Boussinesq equations.
On a fixed -dimensional manifold
, let
denote the space of incompressible flows
, equipped with the smooth topology (in spacetime), and let
denote the space of such flows that are extendible to Euler flows. Our main theorem is
Theorem 1
- (i) (Generic inextendibility) Assume
. Then
is of the first category in
(the countable union of nowhere dense sets in
).
- (ii) (Non-rigidity) Assume
(with an arbitrary metric
). Then
is somewhere dense in
(that is, the closure of
has non-empty interior).
More informally, starting with an incompressible flow , one usually cannot extend it to an Euler flow just by extending the manifold, warping the metric, and adding swirl coefficients, even if one is allowed to select the dimension of the extension, as well as the metric and coefficients, arbitrarily. However, many such flows can be perturbed to be extendible in such a manner (though different perturbations will require different extensions, in particular the dimension of the extension will not be fixed). Among other things, this means that conservation laws such as energy (or momentum, helicity, or circulation) no longer present an obstruction when one is allowed to perform an extension (basically this is because the swirl components of the extension can exchange energy (or momentum, etc.) with the base components in a basically arbitrary fashion.
These results fall short of my hopes to use the ability to extend the manifold to create universal behaviour in Euler flows, because of the fact that each flow requires a different extension in order to achieve the desired dynamics. Still it does seem to provide a little bit of support to the idea that high-dimensional Euler flows are quite “flexible” in their behaviour, though not completely so due to the generic inextendibility phenomenon. This flexibility reminds me a little bit of the flexibility of weak solutions to equations such as the Euler equations provided by the “-principle” of Gromov and its variants (as discussed in these recent notes), although in this case the flexibility comes from adding additional dimensions, rather than by repeatedly adding high-frequency corrections to the solution.
The proof of part (i) of the theorem basically proceeds by a dimension counting argument (similar to that in the proof of Proposition 9 of these recent lecture notes of mine). Heuristically, the point is that an arbitrary incompressible flow is essentially determined by
independent functions of space and time, whereas the warping factors
are functions of space only, the pressure field is one function of space and time, and the swirl fields
are technically functions of both space and time, but have the same number of degrees of freedom as a function just of space, because they solve an evolution equation. When
, this means that there are fewer unknown functions of space and time than prescribed functions of space and time, which is the source of the generic inextendibility. This simple argument breaks down when
, but we do not know whether the claim is actually false in this case.
The proof of part (ii) proceeds by direct calculation of the effect of the warping factors and swirl velocities, which effectively create a forcing term (of Boussinesq type) in the first equation of (1) that is a combination of functions of the Eulerian spatial coordinates (coming from the warping factors) and the Lagrangian spatial coordinates
(which arise from the swirl velocities, which are passively transported by the flow). In a non-empty open subset of
, the combination of these coordinates becomes a non-degenerate set of coordinates for spacetime, and one can then use the Stone-Weierstrass theorem to conclude. The requirement that
be topologically a torus is a technical hypothesis in order to avoid topological obstructions such as the hairy ball theorem, but it may be that the hypothesis can be dropped (and it may in fact be true, in the
case at least, that
is dense in all of
, not just in a non-empty open subset).

14 comments
Comments feed for this article
19 February, 2019 at 10:08 am
Anonymous
Awesome paper,I was just reading how to form eddies,seems I have many years to catch up to become your level
.
19 February, 2019 at 12:05 pm
Anonymous
There is an extraneous “. We say that” at the end of the post
[Corrected, thanks – T.]
19 February, 2019 at 2:20 pm
John Baez
“just obeys the divergence-free relation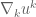 “. You want to add “= 0”.
“. You want to add “= 0”.
I’m just starting to read this blog post. Looks great!
[Corrected, thanks – T.]
20 February, 2019 at 3:59 am
Anonymous
Is there any indication that for large dimension it is easier to establish finite time blowup for some Euler flows?
20 February, 2019 at 6:47 am
Anonymous
Even the best PDE expert, they do not understand Terry’work.Me too.But I has seen a giant bridge across the Pacific of Pro.Tao.
Dr.Tao is not only a mathematician, he is regarded as the Coach of the world’s biggest football team in maths.He is very clever in tactics and strategy in doing maths.Opponent never discover Terry ‘s plot. Today I truly congratuate Terry. Next time I am waiting to be fun from Goldbach strong conjecture from Terry.At any rate , the knight Terry will certainly conquere Goldbach “monster” in early 2019. If this happens early, all that day I am full although I do not eat any more.
Best wishes,
28 February, 2019 at 12:02 am
Anonymous
I completely agree above ” anonymous” professor with such remark.I am not a mathematician.But I am very talented in guess and predictions.When I was a student, I was the fastest and the best accurate in doing multiple choices if comparing with the whole university.When I went out of university,I have many times of arguments with doctor, teacher, engineer,technician,processor….etc.But finally,the victories belong to me.I always win in betting which football team will win in World cup,I also win lottery over 200 times.So,I guarantee that Pro.Tao will do a next great breakthrough after FLT and Poincare conjecture in 2019.You try to imagine that 100 current famous mathematicians like 100 billiard cubes into a tables, and which cube will run into a hole.I affirm that only cube in a hole is certain Pro.Tao
2 March, 2019 at 8:15 am
Anonymous
Oh,regardless of yours’ dislike (10000 dislikes are not meaningful to me).I never lose in betting.This is the first time that I bet against the whole math community.Despite of saying 1000 times, I always claim that Pro.Tao will certainly do a century great breakthrough work in 2019.When I was a student , at the same time I against 1000 others(including professor),but I finally win.
8 March, 2019 at 6:40 pm
Anonymous
I find myself will agree. All PdE mathematicians bow down at Terry. Even expert find his Navier Stoke don’t blow up in Sobolev space, which I thought ever since my child years. In June 2016 Terry proves the Riemann hypotheses, which will change number theory ever since the days of Gauss and Fermat. If only he put the proof on ArXiV soon.
20 February, 2019 at 8:37 am
Terence Tao
Well, every smooth solution to the Euler equation ,
,  in some
in some  -dimensional manifold
-dimensional manifold  can be automatically lifted to a solution
can be automatically lifted to a solution  ,
, 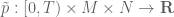 in a
in a 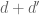 -dimensional product manifold
-dimensional product manifold 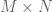 (for an arbitrary
(for an arbitrary 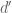 -dimensional manifold
-dimensional manifold  ) by considering the “purely horizontal” flow
) by considering the “purely horizontal” flow
and
for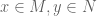 , where
, where 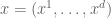 denote local coordinates for the
denote local coordinates for the  variable. As a consequence, if one can prove global regularity in higher dimensions, one automatically gets global regularity in lower dimensions as a consequence; contrapositively, if one can construct a lower dimensional example of finite time blowup, one also gets finite time blowup examples in all higher dimensions. So if one is set on proving finite time blowup, it ought to be easier to do so in higher dimensions.
variable. As a consequence, if one can prove global regularity in higher dimensions, one automatically gets global regularity in lower dimensions as a consequence; contrapositively, if one can construct a lower dimensional example of finite time blowup, one also gets finite time blowup examples in all higher dimensions. So if one is set on proving finite time blowup, it ought to be easier to do so in higher dimensions.
20 February, 2019 at 5:28 am
Richard Taylor
Once bitten twice shy, Terry? ;)
23 February, 2019 at 6:51 am
Anonymous
By compactifying the spacetime manifold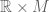 and considering the subgroup of automorphisms preserving the PDE system, if for some initial data there is a blowup at some spacetime point with corresponding time coordinate
and considering the subgroup of automorphisms preserving the PDE system, if for some initial data there is a blowup at some spacetime point with corresponding time coordinate  and there is an automorphism preserving the PDE system and sending this blowup point (with
and there is an automorphism preserving the PDE system and sending this blowup point (with  ) to a point with
) to a point with 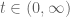 , it seems that such automorphism “transfers” the infinite-time blowup to a finite-time blowup. Hence it seems helpful to study this subgroup of spacetime automorphisms which preserve the PDE system.
, it seems that such automorphism “transfers” the infinite-time blowup to a finite-time blowup. Hence it seems helpful to study this subgroup of spacetime automorphisms which preserve the PDE system.
11 March, 2019 at 3:17 pm
Navies – Pages
[…] which is not quite incompressible (due to the failure of the volume preservation condition (2) in this case) but still satisfies a system of equations (coupled with a passive scalar […]
7 May, 2021 at 2:20 am
Cuatro matemáticos demuestran que era imposible predecir el destino de 29.000 patitos de goma en el mar – Info-spain
[…] la red social Twitter, se enteró de que el investigador australiano Terence Tao había publicado en su blog los últimos detalles de su batalla para resolver ese problema del milenio. Tao fue un niño […]
7 May, 2021 at 2:17 pm
Cuatro matemáticos demuestran que era imposible predecir el destino de 29.000 patitos de goma en el mar » Mascarillas para protección del coronavirus
[…] la red social Twitter, se enteró de que el investigador australiano Terence Tao había publicado en su blog los últimos detalles de su batalla para resolver ese problema del milenio. Tao fue un niño […]