We consider the incompressible Euler equations on the (Eulerian) torus , which we write in divergence form as
is the (inverse) Euclidean metric. Here we use the summation conventions for indices such as
(reserving the symbol
for other purposes), and are retaining the convention from Notes 1 of denoting vector fields using superscripted indices rather than subscripted indices, as we will eventually need to change variables to Lagrangian coordinates at some point. In principle, much of the discussion in this set of notes (particularly regarding the positive direction of Onsager’s conjecture) could also be modified to also treat non-periodic solutions that decay at infinity if desired, but some non-trivial technical issues do arise non-periodic settings for the negative direction.
As noted previously, the kinetic energy
But what is the precise level of regularity needed in order to for this anomalous energy dissipation to occur? To make this question precise, we need a quantitative notion of regularity. One such measure is given by the Hölder space for
, defined as the space of continuous functions
whose norm
Conjecture 1 (Onsager’s conjecture) Letand
, and let
.
- (i) If
, then any weak solution
to the Euler equations (in the Leray form
) obeys the energy conservation law (3).
- (ii) If
, then there exist weak solutions
to the Euler equations (in Leray form) which do not obey energy conservation.
This conjecture was originally arrived at by Onsager by a somewhat different heuristic derivation; see Remark 7. The numerology is also compatible with that arising from the Kolmogorov theory of turbulence (discussed in this previous post), but we will not discuss this interesting connection further here.
The positive part (i) of Onsager conjecture was established by Constantin, E, and Titi, building upon earlier partial results by Eyink; the proof is a relatively straightforward application of Littlewood-Paley theory, and they were also able to work in larger function spaces than (using
-based Besov spaces instead of Hölder spaces, see Exercise 3 below). The negative part (ii) is harder. Discontinuous weak solutions to the Euler equations that did not conserve energy were first constructed by Sheffer, with an alternate construction later given by Shnirelman. De Lellis and Szekelyhidi noticed the resemblance of this problem to that of the Nash-Kuiper theorem in the isometric embedding problem, and began adapting the convex integration technique used in that theorem to construct weak solutions of the Euler equations. This began a long series of papers in which increasingly regular weak solutions that failed to conserve energy were constructed, culminating in a recent paper of Isett establishing part (ii) of the Onsager conjecture in the non-endpoint case
in three and higher dimensions
; the endpoint
remains open. (In two dimensions it may be the case that the positive results extend to a larger range than Onsager’s conjecture predicts; see this paper of Cheskidov, Lopes Filho, Nussenzveig Lopes, and Shvydkoy for more discussion.) Further work continues into several variations of the Onsager conjecture, in which one looks at other differential equations, other function spaces, or other criteria for bad behavior than breakdown of energy conservation. See this recent survey of de Lellis and Szekelyhidi for more discussion.
In these notes we will first establish (i), then discuss the convex integration method in the original context of the Nash-Kuiper embedding theorem. Before tackling the Onsager conjecture (ii) directly, we discuss a related construction of high-dimensional weak solutions in the Sobolev space for
close to
, which is slightly easier to establish, though still rather intricate. Finally, we discuss the modifications of that construction needed to establish (ii), though we shall stop short of a full proof of that part of the conjecture.
We thank Phil Isett for some comments and corrections.
— 1. Energy conservation for sufficiently regular weak solutions —
We now prove the positive part (i) of Onsager’s conjecture, which turns out to be a straightforward application of Littlewood-Paley theory. We need the following relation between Hölder spaces and Littlewood-Paley projections:
Exercise 2 Letfor some
and
. Establish the bounds
Let be a weak solution to the Euler equations for some
, thus
To treat (7), we use Exercise 2 to conclude that
As shown by Constantin, E, and Titi, the Hölder regularity in the above result can be relaxed to Besov regularity, at least in non-endpoint cases:
Exercise 3 Let. Define the Besov space
to be the space of functions
such that the Besov space norm
Show that if
is a weak solution to the Euler equations, the energy
is conserved in time.
The endpoint case of the above exercise is still open; however energy conservation in the slightly smaller space
is known thanks to the work of Cheskidov, Constantin, Friedlander, and Shvydkoy (see also this paper of Isett for further discussion, and this paper of Isett and Oh for an alternate argument that also works on Riemannian manifolds).
As observed by Isett (see also the recent paper of Colombo and de Rosa), the above arguments also give some partial information about the energy in the low regularity regime:
Exercise 4 Letbe a weak solution to the Euler equations for
.
- (i) If
, show that the energy
is a
function of time. (Hint: express the energy as the uniform limit of
.)
- (ii) If
, show that the energy
is a
function of time.
Exercise 5 Letbe a weak solution to the Navier-Stokes equations for some
with initial data
. Establish the energy identity
Remark 6 An alternate heuristic derivation of thethreshold for the Onsager conjecture is as follows. If
, then from Exercise 2 we see that the portion of
that fluctuates at frequency
has amplitude
at most
; in particular, the amount of energy at frequencies
is at most
. On the other hand, by the heuristics in Remark 11 of 254A Notes 3, the time
needed for the portion of the solution at frequency
to evolve to a higher frequency scale such as
is of order
. Thus the rate of energy flux at frequency
should be
. For
, the energy flux goes to zero as
, and so energy cannot escape to frequency infinity in finite time.
Remark 7 Yet another alternate heuristic derivation of thethreshold arises by considering the dynamics of individual Fourier coefficients. Using a Fourier expansion
the Euler equations may be written as
In particular, the energy
at a single Fourier mode
evolves according to the equation
If
, then we have
for any
, hence by Plancherel’s theorem
which suggests that (up to logarithmic factors) one would expect
to be of magnitude about
. Onsager posited that for typically “turbulent” or “chaotic” flows, the main contributions to (8) come when
have magnitude roughly comparable to that of
, and that the various summands should not be correlated strongly to each other. For
, one might expect about
significant terms in the sum, which according to standard “square root cancellation heuristics” (cf. the central limit theorem) suggests that the sum is about as large as
times the main term. Thus the total flux of energy in or out of a single mode
would be expected to be of size
, and so the total flux in or out of the frequency range
(which consists of
modes
) should be about
. As such, for
the energy flux should decay in
and so there is no escape of energy to frequency infinity, whereas for
such an escape should be possible. Related heuristics can also support Kolmogorov’s 1941 model of the distribution of energy in the vanishing viscosity limit; see this blog post for more discussion. On the other hand, while Onsager did discuss the dynamics of individual Fourier coefficients in his paper, it appears that he arrived at the
threshold by a more physical space based approach, a rigorous version of which was eventually established by Duchon and Robert; see this survey of Eyink and Sreenivasan for more discussion.
— 2. The (local) isometric embedding problem —
Before we develop the convex integration method for fluid equations, we first discuss the simpler (and historically earlier) instance of this technique for the isometric embedding problem for Riemannian manifolds. To avoid some topological technicalities that are not the focus of the present set of notes, we only consider the local problem of embedding a small neighbourhood of the origin
in
into Euclidean space
.
Let be an open neighbourhood of
in
. A (smooth) Riemannian metric on
, when expressed in coordinates, is a family
of smooth maps
for
, such that for each point
, the matrix
is symmetric and positive definite. Any such metric
gives
the structure of an (incomplete) Riemannian manifold
. An isometric embedding of this manifold into a Euclidean space
is a map
which is continuously differentiable, injective, and obeys the equation
, where
is the usual inner product (or dot product) on
. In the differential geometry language from Notes 1, we are looking for an injective map
such that the Euclidean metric
on
pulls back to
via
:
.
The isometric embedding problem asks, given a Riemannian manifold such as , whether there is an isometric embedding from this manifold to a Euclidean space
; for simplicity we only discuss the simpler local isometric embedding problem of constructing an isometric immersion of
into
for some sufficiently small neighbourhood
of the origin. In particular for the local problem we do not need to worry about injectivity since (9) ensures that the derivative map
is injective at the origin, and hence
is injective near the origin by the inverse function theorem (indeed it is an immersion near the origin).
It is a celebrated theorem of Nash (discussed in this previous blog post) that the isometric embedding problem is possible in the smooth category if the dimension is large enough. For sake of discussion we just present the local version:
Theorem 8 (Nash embedding theorem) Suppose thatis sufficiently large depending on
. Then for any smooth metric
on a neighbourhood
of the origin, there is a smooth local isometric embedding
on some smaller neighbourhood
of the origin.
The optimal value of depending on
is not completely known, but it grows roughly quadratically in
. Indeed, in this paper of Günther it is shown that one can take
Proposition 9 Suppose that. Then there exists a smooth Riemannian metric
on an open neighbourhood
of the origin in
such that there is no smooth embedding
from any smaller neighbourhood
of the origin to
.
Proof: Informally, the reason for this is that the given field has
degrees of freedom (which is the number of independent fields after accounting for the symmetry
), but there are only
degrees of freedom for the unknown
. To make this rigorous, we perform a Taylor expansion of both
and
around the origin up to some large order
, valid for a sufficiently small neighbourhood
:
Remark 10 If one replaces “smooth” with “analytic”, one can reverse the arguments here using the Cauchy-Kowaleski theorem and show that any analytic metric oncan be locally analytically embedded into
; this is a classical result of Cartan and Janet.
Apart from the slight gap in dimensions, this would seem to settle the question of when a -dimensional metric may be locally isometrically embedded in
. However, all of the above arguments required the immersion map
to be smooth (i.e.,
), whereas the definition of an isometric embedding only required the regularity of
.
It is a remarkable (and somewhat counter-intuitive) result of Nash and Kuiper that if one only requires the embedding to be in , then one can embed into a much lower dimensional space:
Theorem 11 (Nash-Kuiper embedding theorem) Let. Then for any smooth metric
on a neighbourhood
of the origin, there is a
local isometric embedding
on some smaller neighbourhood
of the origin.
Nash originally proved this theorem with the slightly weaker condition ; Kuiper then obtained the optimal condition
. The case
fails due to curvature obstructions; for instance, if the Riemannian metric
has positive scalar curvature, then small Riemannian balls of radius
will have (Riemannian) volume slightly less than their Euclidean counterparts, whereas any
embedding into
will preserve both Riemannian length and volume, preventing such an isometric embedding from existing.
Remark 12 One striking illustration of the distinction between theand smooth categories comes when considering isometric embeddings of the round sphere
(with the usual metric) into Euclidean space
. It is a classical result (see e.g., Spivak’s book) that the only
isometric embeddings of
in
are the obvious ones coming from composing the inclusion map
with an isometry of the Euclidean space; however, the Nash-Kuiper construction allows one to create an
embedding of
into an arbitrarily small ball! Thus the
embedding problem lacks the “rigidity” of the
embedding problem. This is an instance of a more general principle that nonlinear differential equations such as (10) can become much less rigid when one weakens the regularity hypotheses demanded on the solution.
To prove this theorem we work with a relaxation of the isometric embedding problem. We say that is a short isometric embedding on
if
,
solve the equation
with the matrix
symmetric and positive definite for all
. With the additional unknown field
it is much easier to solve the short isometric problem than the true problem. For instance:
Proposition 13 Let, and let
be a smooth Riemannian metric on a neighbourhood
of the origin in
. There is at least one short isometric embedding
.
Proof: Set and
for a sufficiently small
, where
is the standard embedding, and
the Euclidean metric on
; this will be a short isometric embedding on some neighbourhood of the origin.
To create a true isometric embedding , we will first construct a sequence
of short embeddings with
converging to zero in a suitable sense, and then pass to a limit. The key observation is then that by using the fact that the positive matrices lie in the convex hull of the rank one matrices, one can add a high frequency perturbation to the first component
of a short embedding
to largely erase the error term
, replacing it instead with a much higher frequency error.
We now prove Theorem 11. The key iterative step is
Theorem 14 (Iterative step) Let, let
be a closed ball in
, let
be a smooth Riemannian metric on
, and let
be a short isometric embedding on
. Then for any
, one can find a short isometric embedding
to (11) on
with
Suppose for the moment that we had Theorem 14. Starting with the short isometric embedding on a ball
provided by Proposition 13, we can iteratively apply the above theorem to obtain a sequence of short isometric embeddings
on
with
We prove Theorem 14 through a sequence of reductions. Firstly, we can rearrange it slightly:
Theorem 15 (Iterative step, again) Let, let
be a closed ball in
, let
be a smooth immersion, and let
be a smooth Riemannian metric on
. Then there exists a sequence
of smooth immersions for
obeying the bounds
uniformly on
for
, where
denotes a quantity that goes to zero as
(for fixed choices of
).
Let us see how Theorem 15 implies Theorem 14. Let the notation and hypotheses be as in Theorem 14. We may assume to be small. Applying Theorem 15 with
replaced by
(which will be positive definite for
small enough), we obtain a sequence
of smooth immersions obeying the estimates
To prove Theorem 15, it is convenient to break up the metric into more “primitive” pieces that are rank one matrices:
Lemma 16 (Rank one decomposition) Letbe a closed ball in
, and let
be a smooth Riemannian metric on
. Then there exists a finite collection
of unit vectors
in
, and smooth functions
, such that
for all
. Furthermore, for each
, at most
of the
are non-zero.
Remark 17 Strictly speaking, the unit vectorsshould belong to the dual space
of
rather than
itself, in order to have the index
appear as subscripts instead of superscripts. A similar consideration occurs for the frequency vectors
from Remark 7. However, we will not bother to distinguish between
and
here (since they are identified using the Euclidean metric).
Proof: Fix a point in
. Then the matrix
is symmetric and positive definite; one can thus write
, where
is an orthonormal basis of (column) eigenvectors of
and
are the eigenvalues (we suppress for now the dependence of these objects on
). Using the parallelogram identity
Remark 18 Informally, Lemma 16 lets one synthesize a metricas a “convex integral” of rank one pieces, so that if the problem at hand has the freedom to “move” in the direction of each of these rank one pieces, then it also has the freedom to move in the direction
, at least if one is working in low enough regularities that one can afford to rapidly change direction from one rank one perturbation to another. This convex integration technique was formalised by Gromov in his interpretation of the Nash-Kuiper method as part of his “
-principle“, which we will not discuss further here.
One can now deduce Theorem 15 from
Theorem 19 (Iterative step, rank one version) Let, let
be a closed ball in
, let
be a smooth immersion, let
be a unit vector, and let
be smooth. Then there exists a sequence
of smooth immersions for
obeying the bounds
uniformly on
for
. Furthermore, the support of
is contained in the support of
.
Indeed, suppose that Theorem 19 holds, and we are in the situation of Theorem 15. We apply Lemma 16 to obtain the decomposition
It remains to prove Theorem 19. We note that the requirement that be an immersion will be automatic from (15) for
large enough since
was already an immersion, making the matrix
positive definite uniformly for
, and this being unaffected by the addition of the
perturbation and the positive semi-definite rank one matrix
.
Writing , it will suffice to find a sequence of smooth maps
supported in the support of
and obeying the approximate difference equation
.
To locate these functions , we use the method of slow and fast variables. First we observe by applying a rotation that we may assume without loss of generality that
is the unit vector
, thus
. We then use the ansatz
Remark 20 Informally, one should think of functionsthat are independent of the fast variable
as being of “low frequency”, and conversely functions that have mean zero in the fast variable
(thus
for all
) as being of “high frequency”. Thus for instance any smooth function on
can be uniquely decomposed into a “low frequency” component and a “high frequency” component, with the two components orthogonal to each other. In later sections we will start inverting “fast derivatives”
on “high frequency” functions, which will effectively gain important factors of
in the analysis. See also the table below for the dictionary between ordinary physical coordinates and fast-slow coordinates.
| Position | Slow variable |
| Fast variable | Fast variable |
| Function | Function |
| | |
| Low-frequency function | Function |
| High-frequency function | Function |
| N/A | Slow derivative |
| N/A | Fast derivative |
If we expand out using the chain rule, using and
to denote partial differentiation in the coordinates of the slow and fast variables respectively, and noting that all terms with at least one power of
can be absorbed into the
error, we see that we will be done as long as we can construct
to obey the bounds
are viewed as functions of the slow variable
only. The original approach of Nash to solve this equation was to use a function
that was orthogonal to the entire gradient of
, thus
. Taking derivatives in
one would conclude that
Lemma 21 (Constructing an orthogonal frame) Letbe an immersion. If
, then there exist smooth vector fields
such that at every point
,
are unit vectors orthogonal to each other and to
for
.
Proof: Applying the Gram-Schmidt process to the linearly independent vectors for
, we can find an orthonormal system of vectors
, depending smoothly on
, whose span is the same as the span of the
. Our task is now to find smooth functions
solving the system of equations
.
For this is possible at the origin
from the Gram-Schmidt process. Now we extend in the
direction to the line segment
. To do this we evolve the fields
by the parallel transport ODE
This concludes Nash’s proof of Theorem 11 when . Now suppose that
. In this case we cannot locate two unit vector fields
orthogonal to each other and to the entire gradient of
; however, we may still obtain one such vector field
by repeating the above arguments. By Gram-Schmidt, we can then locate a smooth unit vector field
which is orthogonal to
and to
for
, but for which the quantity
is positive. If we use the “Kuiper corrugation” ansatz
This can be done by an explicit construction:
Exercise 22 (One-dimensional corrugation) For any positiveand any
, show that there exist smooth functions
solving the ODE
and which vary smoothly with
(even at the endpoint
), and obey the bounds
(Hint: one can renormalise
. The problem is basically to locate a periodic function
mapping
to the circle
of mean zero and Lipschitz norm
that varies smoothly with
. Choose
for some smooth and small
that is even and compactly supported in
with mean zero on each interval, and then choose
to be odd.)
This exercise supplies the required functions , completing Kuiper’s proof of Theorem 11 when
.
Remark 23 For sake of discussion let us restrict attention to the surface case. For the local isometric embedding problem, we have seen that we have rigidity at regularities at or above
, but lack of regularity at
. The precise threshold at which rigidity occurs is not completely known at present: a result of Borisov (also reproven here) gives rigidity at the
level for
, while a result of de Lellis, Inauen, and Szekelyhidi (building upon a series of previous results) establishes non-rigidity when
. For recent results in higher dimensions, see this paper of Cao and Szekelyhidi.
— 3. Low regularity weak solutions to Navier-Stokes in high dimensions —
We now turn to constructing solutions (or near-solutions) to the Euler and Navier-Stokes equations. For minor technical reasons it is convenient to work with solutions that are periodic in both space and time, and normalised to have zero mean at every time (although the latter restriction is not essential for our arguments, since one can always reduce to this case after a Galilean transformation as in 254A Notes 1). Accordingly, let denote the periodic spacetime
Let (for now, our discussion will apply both to the Navier-Stokes equations
and the Euler equations
). Smooth solutions to Navier-Stokes equations then take the form
Much as we replaced the equation (10) in the previous section with (11), we will consider the relaxed version , known as the Reynolds stress (cf. the Cauchy stress tensor from 254A Notes 0). If
,
,
are smooth solutions to (26), (27), (28), with
having mean zero at every time, then we call
a Navier-Stokes-Reynolds flow (or Euler-Reynolds flow, if
). Note that if
then we recover a solution to the true Navier-Stokes equations. Thus, heuristically, the smaller
is, the closer
and
should become to a solution to the true Navier-Stokes equations. (The Reynolds stress tensor
here is a rank
tensor, as opposed to the rank
tensor
used in the previous section to measure the failure of isometric embedding, but this will not be a particularly significant distinction.)
Note that if is a Navier-Stokes-Reynolds flow, and
,
,
are smooth functions, then
will also be a Navier-Stokes-Reynolds flow if and only if
has mean zero at every time, and
obeys the difference equation
is a difference Navier-Stokes-Reynolds flow at
.
It will be thus of interest to find, for a given , difference Navier-Stokes-Reynolds flows
at
with
small, as one could hopefully iterate this procedure and take a limit to construct weak solutions to the true Euler equations. The main strategy here will be to choose a highly oscillating (and divergence-free) correction velocity field
such that
approximates
up to an error which is also highly oscillating (and somewhat divergence-free). The effect of this error can then eventually be absorbed efficiently into the new Reynolds stress tensor
. Of course, one also has to manage the other terms
,
,
,
appearing in (29). In high dimensions it turns out that these terms can be made very small in
norm, and can thus be easily disposed of. In three dimensions the situation is considerably more delicate, particularly with regards to the
and
terms; in particular, the transport term
term is best handled by using a local version of Lagrangian coordinates. We will discuss these subtleties in later sections.
To execute above strategy, it will be convenient to have an even more flexible notion of solution, in which is no longer required to be perfectly divergence-free and mean zero, and is also allowed to be slightly inaccurate in solving (29). We say that
is an approximate difference Navier-Stokes-Reynolds flow at
if
,
,
are smooth functions obeying the system
If the error terms , as well as the mean of
, are all small, one can correct an approximate difference Navier-Stokes-Reynolds flow
to a true difference Navier-Stokes-Reynolds flow
with only small adjustments:
Exercise 24 (Removing the error terms) Letbe a Navier-Stokes-Reynolds flow, and let
be an approximate difference Navier-Stokes-Reynolds flow at
. Show that
is an approximate difference Navier-Stokes-Reynolds flow at
, where
and
is the mean of
, thus
(Hint: one will need at some point to show that
has mean zero in space at every time; this can be achieved by integrating (32) in space.)
Because of this exercise we will be able to tolerate the error terms if they (and the mean
) are sufficiently small.
As a simple corollary of Exercise 24, we have the following analogue of Proposition 13:
Proposition 25 Let. Then there exist smooth fields
,
such that
is a Navier-Stokes-Reynolds flow. Furthermore, if
is supported in
for some compact time interval
, then
can be chosen to also be supported in this region.
Proof: Clearly is an approximate difference Navier-Stokes-Reynolds flow at
, where
Now, we show that, in sufficiently high dimension, a Navier-Stokes-Reynolds flow can be approximated (in an
sense) as the limit of Navier-Stokes-Reynolds flows
, with the Reynolds stress
going to zero.
Proposition 26 (Weak improvement of Navier-Stokes-Reynolds flows) Let, and let
be sufficiently large depending on
. Let
be a Navier-Stokes-Reynolds flow. Then for sufficiently large
, there exists a Navier-Stokes-Reynolds flow
obeying the estimates
for all
, and such that
Furthermore, if
is supported in
for some interval
, then one can arrange for
to be supported on
for any interval
containing
in its interior (at the cost of allowing the implied constants in the above to depend also on
).
This proposition can be viewed as an analogue of Theorem 14. For an application at the end of this section it is important that the implied constant in (36) is uniform in the choice of initial flow . The estimate (35) can be viewed as asserting that the new velocity field
is oscillating at frequencies
, at least in an
sense. In the next section, we obtain a stronger version of this proposition with more quantitative estimates that can be iterated to obtain higher regularity weak solutions.
To simplify the notation we adopt the following conventions. Given an -dimensional vector
of differential operators, we use
to denote the
-tuple of differential operators
with
. We use
to denote the
-tuple formed by concatenating
for
. Thus for instance the estimate (35) can be abbreviated as
Proof: We can assume that is non-zero, since if
we can just take
. We may assume that
is supported in
for some interval
(which may be all of
), and let
be an interval containing
in its interior. To abbreviate notation, we allow all implied constants to depend on
.
Assume is sufficiently large. Using the ansatz
It will in fact suffice to construct an approximate difference Navier-Stokes-Reynolds flow at
supported on
and obeying the bounds
, since an application of Exercise 24 and some simple estimation will then give a difference Navier-Stokes-Reynolds flow
obeying the desired estimates (using in particular the fact that
is bounded on
and
, as can be seen from Littlewood-Paley theory; also note that (39) can be used to ensure that the mean of
is very small).
To construct this approximate solution, we again use the method of fast and slow variables. Set , and introduce the fast-slow spacetime
, which we coordinatise as
; we use
to denote partial differentiation in the coordinates of the slow variable
, and
to denote partial differentiation in the coordinates of the fast variable
. We also use
as shorthand for
. Define an approximate fast-slow solution to the difference Navier-Stokes-Reynolds equation at
(at the frequency scale
) to be a tuple
of smooth functions
,
,
that obey the system of equations
Let denote the tuple
. Suppose that for any sufficiently large
, we can construct an approximate fast-slow solution
to the difference equations at
supported on supported on
that obeys the bounds
. (Informally, the presence of the derivatives
means that the fields involved are allowed to oscillate in time at wavelength
, in the slow variable
at wavelength
, and in the fast variable
at wavelength
.) From (46) and the choice of
we then have
It remains to construct an approximate fast-slow solution supported on
with the required bounds (46)–(51). Actually, in this high-dimensional setting we can afford to simplify the situation here by removing some of the terms (and in particular eliminating the role of the reference velocity field
). Define a simplified fast-slow solution at
to be a tuple
of smooth functions on
obeying the simplified equations
of smooth functions on
supported on
obeying the bounds
, then the
will be an approximate fast-slow solution supported on
obeying the required bounds (46)–(51), where
Now we need to construct a simplified fast-slow solution supported on
obeying the bounds (56)–(60). We do this in stages, first finding a solution that cancels off the highest order terms
and
, and also such that
has mean zero in the fast variable
(so that it is “high frequency” in the sense of Remark 20). This still leads to fairly large values of
and
, but we will then apply a “divergence corrector” to almost completely eliminate
, followed by a “stress corrector” that almost completely eliminates
, at which point we will be done.
We turn to the details. Our preliminary construction of the velocity field will be a “Mikado flow”, consisting of flows along narrow tubes. (Earlier literature used other flows, such as Beltrami flows; however, Mikado flows have the advantage of being localisable to small subsets of spacetime, which is particularly useful in high dimensions.) We need the following modification of Lemma 16:
Exercise 27 Letbe a compact subset of the space of positive definite
matrices
. Show that there exist non-zero lattice vectors
and smooth functions
for some
such that
for all
. (This decomposition is essentially due to de Lellis and Szekelyhidi. The subscripting and superscripting here is reversed from that in Lemma 16; this is because we are now trying to decompose a rank
tensor rather than a rank
tensor.)
We would like to apply this exercise to the matrix with entries . We thus need to select the pressure
so that this matrix is positive definite. There are many choices available for this pressure; we will take
Now for each , the closed subgroup
is a one-dimensional subset of
, so the
-neighbourhood of this subgroup has measure
; crucially, this will be a large negative power of
when
is very large. let
be a translate of this
-neighbourhood such that all the
are disjoint; this is easily accomplished by the probabilistic method for
large enough, translating each of the
by an independent random shift and noting that the probability of a collision goes to zero as
(here we need the fact that we are in at least three dimensions).
Let be a large integer (depending on
) to be chosen later. For any
, let
be a scalar test function supported on
that is constant in the
direction, thus
Let denote the function
This looks worse than (56)–(60). However, observe that is supported on the set
, which has measure
, which for
large enough can be taken to be (say)
. Thus by Cauchy-Schwarz one has
. Also, from construction (particularly (66)) we see that
is of mean zero in the
variable (thus it is “high frequency” in the sense of Remark 20).
We are now a bit closer to (56)–(60), but our bounds on are not yet strong enough. We now apply a “divergence corrector” to make
much smaller. Observe from construction that
where
We have now achieved the bound (59); the remaining estimate that needs to be corrected for is (60). This we can do by a modification of the previous argument, where we now work to reduce the size of rather than
. Observe that as
is “high frequency” (mean zero in the
variable), one can write
As an application of this proposition we construct a low-regularity weak solution to high-dimensional Navier-Stokes that does not obey energy conservation. More precisely, for any , let
be the Banach space of periodic functions
which are divergence free, and of mean zero at every time. For
, define a time-periodic weak
solution
of the Navier-Stokes (or Euler, if
) equations to be a function
that solves the equation
Corollary 28 (Low regularity non-trivial weak solutions) Assume that the dimensionis sufficiently large. Then for any
, there exists a periodic weak
solution
to Navier-Stokes which equals zero at time
, but is not identically zero. In particular, periodic weak
solutions are not uniquely determined by their initial data, and do not necessarily obey the energy inequality
Proof: Let be an element of
that is supported on
and is not identically zero (it is easy to show that such an element exists). By Proposition 25, we may then find a Navier-Stokes-Reynolds flow
also supported on
. Let
be sufficiently large. By applying Proposition 26 repeatedly (with say
) and with a sufficiently rapidly increasing sequence
, we can find a sequence
of Navier-Stokes-Reynolds flows supported on (say)
obeying the bounds
— 4. High regularity weak solutions to Navier-Stokes in high dimensions —
Now we refine the above arguments to give a higher regularity version of Corollary 28, in which we can give the weak solutions almost half a derivative of regularity in the Sobolev scale:
Theorem 29 (Non-trivial weak solutions) Let, and assume that the dimension
is sufficiently large depending on
. Then for any
, there exists a periodic weak
solution
which equals zero at time
, but is not identically zero. In particular, periodic weak
solutions are not uniquely determined by their initial data, and do not necessarily obey the energy inequality (74).
This result is inspired by a three-dimensional result of Buckmaster and Vicol (with a small value of ) and a higher dimensional result of Luo (taking
, and restricting attention to time-independent solutions). In high dimensions one can create fairly regular functions which are large in
type norms but tiny in
type norms; when using the Sobolev scale
to control the solution
(and
type norms to measure an associated stress tensor), this has the effect of allowing one to treat as negligible the linear terms
in (variants of) the Navier-Stokes equation, as well as interaction terms between low and high frequencies. As such, the analysis here is simpler than that required to establish the Onsager conjecture. The construction used to prove this theorem shows in fact that periodic weak
solutions are in some sense “dense” in
, but we will not attempt to quantify this fact here.
In the proof of Corollary 28, we took the frequency scales to be extremely rapidly growing in
. This will no longer be good enough for proving Theorem 29, and in fact we need to take a fairly dense set of frequency scales in which
for a small
. In order to do so, we have to replace Proposition 26 with a more quantitative version in which the dependence of bounds on the size of the original Navier-Stokes-Reynolds flow
is made much more explicit.
We turn to the details. We select the following parameters:
- A regularity
;
- A quantity
, assumed to be sufficiently small depending on
;
- An integer
, assumed to be sufficiently large depending on
; and
- A dimension
, assumed to be sufficiently large depending on
.
As before, we abbreviate as
. We write
for the spatial gradient to distinguish it from the time derivative
.
The main iterative statement (analogous to Theorem 14) starts with a Navier-Stokes-Reynolds flow oscillating at spatial scales up to some small wavelength
, and modifies it to a Navier-Stokes-Reynolds flow
oscillating at a slightly smaller wavelength
, with a smaller Reynolds stress. It can be viewed as a more quantitative version of Proposition 26.
Theorem 30 (Iterative step) Letbe sufficiently large depending on the parameters
. Set
. Suppose that one has a Navier-Stokes-Reynolds flow
obeying the estimates
for some
. Set
. Then there exists a Navier-Stokes-Reynolds flow
obeying the estimates
Furthermore, if
is supported on
for some interval
, then one can ensure that
is supported in
, where
is the
-neighbourhood of
.
Let us assume Theorem 30 for the moment and establish Theorem 29. Let be chosen to be supported on (say)
and not be identically zero. By Proposition 25, we can then find a Navier-Stokes-Reynolds flow
supported on
. Let
be a sufficiently large parameter, and set
, then the hypotheses (75), (76) will be obeyed for
large enough. Set
for all
. By iteratively applying Theorem 30, we may find a sequence
of Navier-Stokes-Reynolds flows, all supported on (say)
, obeying the bounds
It remains to establish Theorem 30. It will be convenient to introduce the intermediate frequency scales
Before we begin the rigorous argument, we first give a heuristic explanation of the numerology. The initial solution has about
degrees of regularity controlled at
. For technical reasons we will upgrade this to an infinite amount of regularity, at the cost of worsening the frequency bound slightly from
to
. Next, to cancel the Reynolds stress
up to a smaller error
, we will perturb
by some high frequency correction
, basically oscillating at spatial frequency
(and temporal frequency
), so that
is approximately equal to
(minus a pressure term) after averaging at spatial scales
. Given the size bound (76), one expects to achieve this with
of
norm about
. By exploiting the small gap between
and
, we can make
concentrate on a fairly small measure set (of density something like
), which in high dimension allows us to make linear terms such as
and
(as well as the correlation terms
and
) negligible in size (as measured using
type norms) when compared against quadratic terms such as
(cf. the proof of Proposition 26). The defect
will then oscillate at frequency
, but can be selected to be of size about
in
norm, because can choose
to cancel off all the high-frequency (by which we mean
or greater) contributions to this term, leaving only low frequency contributions (at frequencies
or below). Using the ellipticity of the Laplacian, we can then express this defect as
where the
norm of
is of order
We now turn to the rigorous details. In a later part of the argument we will encounter a loss of derivatives, in that the new Navier-Stokes-Reynolds flow has lower amounts of controlled regularity (in both space and time) than the Navier-Stokes-Reynolds flow
used to construct it. To counteract this loss of derivatives we need to perform an initial mollification step, which improves the amount of regularity from
derivatives in space and time to an unlimited number of derivatives in space and time, at the cost of worsening the estimates on
slightly (basically by replacing
with
).
Proposition 31 (Mollification) Let the notation and hypotheses be as above. Then we can find a Navier-Stokes-Reynolds flowobeying the estimates
and
for all
, and such that
and
Furthermore, if
is supported on
for some interval
, then one can ensure that
is supported in
, where
is the
-neighbourhood of
.
We remark that this sort of mollification step is now a standard technique in any iteration scheme that involves loss of derivatives, including the Nash-Moser iteration scheme that was first used to prove Theorem 8.
Proof: Let be a bump function (depending only on
) supported on the region
of total mass
, and define the averaging operator
on smooth functions
by the formula
Observe that are convolution operators and thus commute with each other and with the partial derivatives
. If we apply the operator
to (26), (27), (28), we see that
is Navier-Stokes-Reynolds flow, where
We abbreviate . For any
, we have
From (81) and decomposing as linear combinations of
, we have
Finally we prove (78). By the triangle inequality it suffices to show that . The claim (83) follows from (81), (76), after writing
as a linear combination of
and noting that
. For (84), if we again write
as a linear combination of
and uses (81) and the Leibniz rule, one can bound the left-hand side of (84) by
We return to the proof of Theorem 30. We abbreviate . Let
be the Navier-Stokes-Reynolds flow constructed by Proposition 31. By using the ansatz
Now, we pass to fast and slow variables. Let denote the tuple
Exercise 32 By using the method of fast and slow variables as in the previous section, show that to construct the approximate Navier-Stokes-Reynolds flowat
obeying the bounds (86), (88), (89), (90), (91), it suffices to locate an approximate fast-slow solution
to the difference Navier-Stokes-Reynolds equation at
(at frequency scale
rather than
) and supported in
that obey the bounds
As in the previous section, we can then pass to simplified fast-slow soutions:
Exercise 33 Show that to construct the approximate fast-slow solutionto the difference equation at
obeying the estimates of the previous exercise, it will in fact suffice to locate a simplified fast-slow solution
at
(again at frequency scale
) supported on
, obeying the bounds (92), (93), (95), (96) and
(Hint: one will need the estimate
from Proposition 31.)
Now we need to construct a simplified fast-slow solution at
supported on
obeying the bounds (92), (93), (95), (96), (97). As in the previous section, we do this in stages, first finding a solution that cancels off the top order terms
and
, and also such that
is “ high frequency” (mean zero in
). Then we apply a divergence corrector to completely eliminate
, followed by a stress corrector that almost completely eliminates
.
As before, we need to select so that
is positive definite. In the previous section we essentially took
to be a large multiple of
, but now we will need good control on the derivatives of
, which requires a little more care. Namely, we will need the following technical lemma:
Lemma 34 (Smooth polar-type decomposition) There exists a factorisation, where
,
are smooth, supported on
, and obey the estimates
Proof: We may assume that is not identically zero, since otherwise the claim is trivial. For brevity we write
and
. From (78) we have
denote the spacetime cylinder
, and let
denote the maximal function
Strictly speaking we are not quite done because is not supported in
, but if one applies a smooth cutoff function in time that equals
on
(where
is supported in time) and vanishes outside of
, we obtain the required support property without significantly affecting the estimates.
Let be the factorisation given by the above lemma. If we set
for a sufficiently large constant
depending only on
, then
Let be the disjoint tubes in
from the previous section, with width
rather than
. Construct the functions
as in the previous section, and again set
The divergence corrector can be applied without difficulty:
Exercise 35 Show that there is a simplified fast-slow solutionsupported in
obeying the estimates
The crucial thing here is the tiny gain in the third estimate, with the first factor
coming from a “slow” derivative
and the second factor
coming from essentially inverting a “fast” derivative
.
Finally, we apply a stress corrector:
Exercise 36 Show that there is a simplified fast-slow solutionsupported in
obeying the estimates
Again, we have a crucial gain of coming from applying a slow derivative and inverting a fast one.
Since
— 5. Constructing low regularity weak solutions to Euler —
Throughout this section, we specialise to the Euler equations in the three-dimensional case
(although all of the arguments here also apply without much modification to
as well). In this section we establish an analogue of Corollary 28:
Proposition 37 (Low regularity non-trivial weak solutions) There exists a periodic weaksolution
to Euler which equals zero at time
, but is not identically zero.
This result was first established by de Lellis and Szekelyhidi. Our approach will deviate from the one in that paper in a number of technical respects (for instance, we use Mikado flows in place of Beltrami flows, and we place more emphasis on the method of fast and slow variables). A key new feature, which was not present in the high-dimensional Sobolev-scale setting, is that the material derivative term in the difference Euler-Reynolds equations is no longer negligible, and needs to be treated by working with an ansatz in Lagrangian coordinates (or equivalently, an ansatz transported by the flow). (This use of Lagrangian coordinates is implicit in the thesis of Isett, this paper of de Lellis and Szekelyhidi, and in the later work of Isett.)
Just as Corollary 28 was derived from Proposition 26, the above proposition may be derived from
Proposition 38 (Weak improvement of Euler-Reynolds flows) Letbe an Euler-Reynolds flow supported on a strict compact subinterval
. Let
be another interval in
containing
in its interior. Then for sufficiently large
, there exists a Euler-Reynolds flow
supported in
obeying the estimates
for all
, and such that
also, we have a decomposition
where
are smooth functions obeying the bounds
The point of the decomposition (115) is that it (together with the smallness bounds (116)) asserts that the velocity correction is mostly “high frequency” in nature, in that its low frequency components are small. Together with (112), the bounds roughly speaking assert that it is only the frequency
components of
that can be large in
norm. Unlike the previous estimates, it will be important for our arguments that
is supported in a strict subinterval
of
, because we will not be able to extend Lagrangian coordinates periodically around the circle. Actually the long-time instability of Lagrangian coordinates causes significant technical difficulties to overcome when one wants to construct solutions in higher regularity Hölder spaces
, and in particular for
close to
; we discuss this in the next section.
Exercise 39 Deduce Proposition 37 from Proposition 38. (The decomposition (116) is needed to keepclose to
in a very weak topology – basically the
topology – but one which is still sufficent to ensure that the limiting solution constructed is not identically zero.)
We now begin the proof of Proposition 38, repeating many of the steps used to prove Proposition 26. As before we may assume that is non-zero, and that
is supported in
. We can assume that
is also a strict subinterval of
.
Assume is sufficiently large; by rounding we may assume that
is a natural number. Using the ansatz
As before, we permit ourselves some error:
Exercise 40 Show that it suffices to construct an approximate difference Euler-Reynolds flowat
supported on
and obeying the bounds
for
, and for which we have a decomposition
obeying (116).
It still remains to construct the approximate difference Euler-Reynolds flow obeying the claimed estimates. By definition, has to obey the system of equations
is divergence-free, the first equation (122) may be rewritten as
is the material Lie derivative of
, thus
in (126) will turn out to be rather harmless; the main new difficulty is dealing with the material Lie derivative term
. We will therefore invoke Lagrangian coordinates in order to convert the material Lie derivative
into the more tractable time derivative
(at the cost of mildly complicating all the other terms in the system).
We introduce a “Lagrangian torus” that is an isomorphic copy of the Eulerian torus
; as in the previous section, we parameterise this torus by
, and adopt the usual summation conventions for the indices
. Let
be a trajectory map for
, that is to say a smooth map such that for every time
, the map
is a diffeomorphism and one obeys the ODE
Recall from Notes 1 that
- (i) Any Eulerian scalar field
on
can be pulled back to a Lagrangian scalar field
on
by the formula
- (ii) Any Eulerian vector field
on
can be pulled back to a Lagrangian vector field
on
by the formula
whereis the inverse of the matrix
, defined by
and - (iii) Any Eulerian rank
tensor
on
, can be pulled back to a Lagrangian rank
tensor
on
by the formula
Exercise 41 (Pullback and divergence)
- (i) If
is a smooth Eulerian vector field, show that the pullback of the divergence of
equals the divergence of the pullback of
:
(Hint: you will need to use the fact that
is volume-preserving. Similarly to Lemma 3 and Exercise 4 of Notes 1, one can establish this either using the laws of integration or the laws of differentiation.).
- (ii) Show that there exist smooth functions
for
with the following property: for any smooth Eulerian rank
tensor
on
, with divergence
, one has
(In fact,
is the Christoffel symbol
associated with the pullback
of the Euclidean metric – but we will not need this precise formula. The right-hand side may also be written (in Penrose abstract index notation) as
, where
is the covariant derivative associated to
.)
- (iii) Show that for any smooth Eulerian vector fields
on
with
, one has
(Hint: use (i), (ii), and the Leibniz rule.)
As remarked upon in the exercise, these calculations can be streamlined using the theory of the covariant derivative in Riemannian geometry; we will not develop this theory further here, but see for instance these two blog posts.
If one now applies the pullback operation to the system (126), (123), (124), (125) (and uses Exercise 16 from Notes 1 to convert the material Lie derivative into the ordinary time derivative) one obtain the equivalent system
This problem looks complicated, but the net effect of moving to the Lagrangian formulation is to arrive at a problem that is nearly identical to the Eulerian one, but in which the material Lie derivative has been replaced by the ordinary time derivative
, and several lower order terms with smooth variable coefficients have been added to the system.
Now that the dangerous transport term in the material Lie derivative has been eliminated, it is now safe to use the method of fast-slow variables, but now on the Lagrangian torus rather than the Eulerian torus
. We now parameterise the fast torus
by
(thus we think of
now as a “Lagrangian fast torus” rather than a “Eulerian fast torus”) and use the ansatz
If is chosen to be “high frequency” (mean zero in the fast variable
), then we can automatically obtain the estimate (148), as one may obtain the decomposition (142) with
As in previous sections, we can relax the conditions on and
:
Exercise 42
- (i) (Stress corrector) Show that we may replace the condition (147) with the condition that
for all
, and that
is of high frequency (mean zero in
). (Hint: add a corrector of size
to
,
so that the main term
now cancels off
, and the other terms created by the correction are of size
and of mean zero in
. Then iterate.)
- (ii) (Divergence corrector) After performing the modifications in (i), show that we may replace the condition (146) with the condition that
for all
, and that
has mean zero in
. (Note that correcting for
will modify
by
, but this will make a negligible contribution to (149) for
large enough.)
We can now repeat the Mikado flow construction from previous sections:
Exercise 43 Set. Construct a smooth vector field
supported on
, with
of mean zero in
, obeying the equations
and such that
is of mean zero in
, obeying the bounds (144) for all
. Also show that for a sufficiently large absolute constant
not depending on
, one can ensure that the matrix with entries
is positive semi-definite at every point
. (Hint: You will need to apply Lemma 34 in order to place a certain positive definite matrix in a compact set independent of
, so that the number
of rank one pieces produced by Exercise 27 is also independent of
.)
If we now set
— 6. Constructing high regularity weak solutions to Euler —
We now informally discuss how to modify the arguments above to establish the negative direction (ii) of Onsager’s conjecture. The full details are rather complicated (and arranged slightly differently from the presentation here), and we refer to Isett’s original paper for details. See also a subsequent paper of Buckmaster, De Lellis, Szekelyhidi, and Vicol for a simplified argument establishing this statement (as well as some additional strengthenings of it).
Let , let
be a small quantity, and let
be a large integer. The main iterative step, analogous to Theorem 30, roughly speaking (ignoring some technical logarithmic factors) takes an Euler-Reynolds flow
obeying the estimates that look like
, and obtains a new Euler-Reynolds flow
close to
that obeys the estimates
; see Lemma 2.1 of Isett’s original paper for a more precise statement (in a slightly different notation), which also includes various estimates on the difference
that we omit here. In contrast to previous arguments, it is useful for technical reasons to not impose time regularity in the estimates. Once this claim is formalised and proved, conclusions such as Onsager’s conjecture follow from the usual iteration arguments.
To achieve this iteration step, the first step is a mollification step analogous to Proposition 31 in which one perturbs the initial flow to obtain additional spatial regularity on the solution. Roughly speaking, this mollification allows one to replace the purely spatial differential operator appearing in (151), (153) with
for
much larger than
(in practice there are some slight additional losses, which we will ignore here).
Now one has to solve the difference equation. We focus on the equation (126) and omit the small errors involving . Suppose for the time being that we could magically replace the material Lie derivative
here by an ordinary time derivative, thus we would be trying to construct
solving an equation such as
However, one also has the terms and
, which (in contrast to the high-dimensional Sobolev scale setting) cannot be ignored in this low-dimensional Hölder scale problem. The natural time scale of oscillation here is
, coming from the usual heuristics concerning the Euler equation (see Remark 11 from 254A Notes 3). With this heuristic,
and
should both behave like
, these expressions would be expected to have amplitude
. They still oscillate at the high frequency
, though, and lead to a stress corrector of magnitude about
. This however remains acceptable for
up to
, which in principle resolves Onsager’s conjecture.
Now we have to remove the “cheat” of replacing the material Lie derivative by the ordinary time derivative. As we saw in the previous section, the natural way to fix this is to work in Lagrangian coordinates. However, we encounter a new problem: if one initialises the trajectory flow map to be the identity at some given time
, then it turns out that one only gets good control on the flow map and its derivatives for times
within the natural time scale
of that initial time
; beyond this, the Gronwall-type arguments used to obtain bounds start to deteriorate exponentially. Because of this, one cannot rely on a “global” Lagrangian coordinate system as in the previous section. To get around this, one needs to partition the time domain
into intervals
of length about
, and construct a separate trajectory map adapted to each such interval. One can then use these “local Lagrangian coordinates” to construct local components
of the velocity perturbation
that obey the required properties on each such interval. This construction is essentially the content of the “convex integration lemma” in Lemma 3.3 of Isett’s paper.
However, a new problem arises when trying to “glue” these local corrections together: two consecutive time intervals
will overlap, and their corresponding local corrections
will also overlap. This leads to some highly undesirable interaction terms between
and
(such as the fast derivative of
) which are very difficult to make small (for instance, one cannot simply ensure that
have disjoint spatial supports as they are constructed using different local Lagrangian coordinate systems). On the other hand, if the original Reynolds stress
had a special structure, namely that it was only supported on every other interval
(i.e., on the
for all
even, or the
for all
odd), then these interactions no longer occur and the iteration step can proceed.
One could try to then resolve the problem by correcting the odd and even interval components of the stress in separate stages (cf. how Theorem 19 can be iterated to establish Theorem 15), but this is inefficient with regards to the
parameter, in particular this makes the argument stop well short of the optimal
threshold. To attain this threshold one needs the final ingredient of Isett’s argument, namely a “gluing approximation” (see Lemma 3.2 of Isett’s paper), in which one tales the (mollified) initial Euler-Reynolds flow
and replaces it with a nearby flow
in which the new Reynolds stress
is only supported on every other interval
. Combining this gluing approximation lemma with the mollification lemma and convex integration lemma gives the required iteration step. (One technical point is that this gluing has to create some useful additional regularity along the material derivative, in the spirit of Remark 38 of Notes 1, as such regularity will be needed in order to justify the convex integration step.)
To obtain this gluing approximation, one takes an -separated sequence of times
, and for each such time
, one solves the true Euler equations with initial data
at
to obtain smooth Euler solutions
on a time interval centred at
of lifespan
, that agree with
at time
. (It is non-trivial to check that these solutions even exist on such an interval, let alone obey good estimates, but this can be done if the initial data was suitably mollified, as is consistent with the heuristics in Remark 11 from 254A Notes 3.) One can then glue these solutions together around the reference solution
by defining

25 comments
Comments feed for this article
10 January, 2019 at 3:23 am
Anonymous
The formatting is messed up (equations showing as raw TeX instead of being rendered) in several places in the article. Btw if you don’t mind my asking, how do you compose these entries? Do you write them out on paper before transcribing to TeX? Or just type TeX directly? Thanks.
10 January, 2019 at 9:50 am
Terence Tao
I didn’t see any raw TeX in the latest version (though there were some overflowing latex displays which I reformatted). It could have been a transient WordPress LaTeX rendering issue.
I use Luca Trevisan’s LateX to WordPress converter, see the bottom of https://terrytao.wordpress.com/about/ as well as http://lucatrevisan.wordpress.com/latex-to-wordpress/ .
10 January, 2019 at 11:18 am
Anonymous
What a wonderful post. Thank you very much Terry
10 January, 2019 at 11:48 am
Auf Achse
Thank you very much for this very interesting post.
It is also worth checking out a beautiful recent survey on the developments towards Onsager‘s conjecture by De Lellis and Székelyhidi:
Click to access 1901.02318.pdf
10 January, 2019 at 4:20 pm
Camillo De Lellis
Dear Terry,
thanks for the beautiful post!
I am not sure whether I have understood correctly your last paragraph that naive attempts to invert the divergence operator lead to poor estimates. But it might be inaccurate, because in this note we do invert the divergence in the most “obvious way”, through an elliptic operator, after the glueing (cf. Section 4):
Click to access Onsager96.pdf
Best,
Camillo
10 January, 2019 at 7:39 pm
Terence Tao
Thanks for this reference, which I had somehow missed!
My discussion was based on that in the start of Section 7 of Isett’s paper https://arxiv.org/pdf/1608.08301.pdf where he says the best estimate he can get from naively inverting the divergence is estimate (50) of that paper which is unsatisfactory. I’m not sure how to reconcile this statement with the estimates in Proposition 4.3 of your paper. Is the point that the commutator estimates with the advective derivative provide a better estimate on the “obvious” choice of antidivergence than what is described in Section 7 of Isett’s paper?
11 January, 2019 at 1:46 am
Camillo De Lellis
Yes, the point is precisely that commuting the antidivergence with the advective derivative gives a better estimate. In a first draft of our proof we did have a lemma where we commuted the antidivergence and the advective derivative. Then we discovered that the proof becomes very elementary and simple if one instead commutes the Biot-Savart operator. So, in the version I linked above, the key is actually Proposition 3.4.
If I remember correctly (I have a bad connection at the moment and I don’t find a copy of Phil’s paper in my laptop), the improvement compared to Phil’s estimate (50) is, in our notation, the factor in our estimate (3.16). The relevant computations on the commutator are between eq. (3.19) and eq. (3.21).
in our estimate (3.16). The relevant computations on the commutator are between eq. (3.19) and eq. (3.21).
11 January, 2019 at 9:11 am
Terence Tao
Thanks for the clarification! The construction and estimation of the antidivergence was the one part of Isett’s paper that I didn’t delve into in detail as it seemed particularly technical; it’s good to know that in fact one can avoid much of this technicality. I have updated the lecture notes accordingly.
16 January, 2019 at 10:16 pm
Phil Isett
About estimating the anti-divergence, one can say a little more about why it works. Commuting with the advective derivative produces a suitable bound for the anti-divergence only if one assumes a priori that the anti-divergence itself already obeys a suitable bound. To get this argument to close depends on the structure of the evolution equation obeyed by the anti-divergence; it is a dynamical estimate that is stronger than the bound one would get by trying to estimate the anti-divergence directly. A similar statement applies to the linearized Euler term that appears in this evolution equation; the direct bound is not sharp enough and the term has to be treated by a dynamical argument.
About improving the timescale: It is possible to improve the timescale of the gluing approximation by using a combination of the approach of Camillo and coauthors (Buckmaster et al.) and my own. Doing so helps to obtain the best known estimate towards the endpoint case of Onsager’s conjecture. The way this improvement works is explained in the last section of my endpoint paper:
https://arxiv.org/abs/1706.01549
Note that obtaining any result of endpoint type requires avoiding power losses in frequency during the iteration, so the strategy I developed in my original proof of Onsager’s conjecture is important for this application because it avoids such power losses.
14 January, 2019 at 9:55 am
Chungachanga
I’m an alien from nearby galaxy, and I wonder how stupid Terence Tao is. The problems he is trying to solve are actualy our elementary school homework.
5 February, 2019 at 8:53 am
test
An alien who can’t spell probably doesn’t know what they’re talking about.
17 January, 2019 at 1:34 am
terminology: equation collapse | Physics Forums
[…] happens. Another term are regular and abnormal solutions, I think. At least Tao used them here: https://terrytao.wordpress.com/2019/01/08/255b-notes-2-onsagers-conjecture/ fresh_42, Jan 17, 2019 at 3:34 […]
17 January, 2019 at 5:10 am
Javohir
Mr. Terence Tao
What kind of email can I send you?
18 January, 2019 at 3:47 am
Javohir
Dear prof. Tao
I have a simple question in math. How can I send you an email?
18 January, 2019 at 6:39 am
Mohd
Hi I learnt from your math thank you for your teaching moreover I am always looking forward for more mathematics journal entries.thank you sir
19 January, 2019 at 8:35 am
Anonymous
Please allow me express my idea here:over three years (2016,2017,2018)Pro.Tao has not still got any medal yet.What a sadly!While everyday , Pro Tao is very patient and active as well as very effective in doing math if comparison with the rest of mathematicians.I hope Pro Tao will make a hattrick in 2019(ProTao will receive Shaw prize,Wolf prize,Abel prize at the same time)I think Pro Tao is very worth having three honors in 2019.Who agrees with me , up like
24 January, 2019 at 2:05 pm
jair2030
Dear Professor Tao,
My name is jai Ramanathan and I really love math,i have a uncountable amount of mental problems and would like your advice in staying in math.I love problem solving but when I an “punished” for solving a question wrong during a assignment and hence affecting my grade,i am an extremely non-creative thinker and a rote learner,would you advise some strategries for me in real analysis courses,your reply would mean the whole world to me.
Many Thanks,
Jai
1 October, 2019 at 4:45 pm
Anonymous
“I have a uncountable amount of mental problems”
same here buddy
28 January, 2019 at 3:12 am
claesjohnson
Hi Terence
I argue that the Clay Problem can be answered by computation:
https://claesjohnson.blogspot.com/2019/01/solution-of-clay-navier-stokes-problem.html
Any comment?
Best regards
Claes
28 January, 2019 at 11:46 am
Anonymous
On a different page of your blog you’ve also disproved P = NP. Wow!
19 February, 2019 at 9:57 am
On the universality of the incompressible Euler equation on compact manifolds, II. Non-rigidity of Euler flows | What's new
[…] equations provided by the “-principle” of Gromov and its variants (as discussed in these recent notes), although in this case the flexibility comes from adding additional dimensions, rather than by […]
8 March, 2019 at 4:46 pm
doing the homework
Possible correction: in the definition of $\mathbf d^i$, the $\grad_x\cdot\grad_y$ should be done $m-1$ times.
[Corrected, thanks – T.]
11 March, 2019 at 3:17 pm
Navies – Pages
[…] Euler equations provided by the “-principle” of Gromov and its variants (as discussed in these recent notes), although in this case the flexibility comes from adding additional dimensions, rather than by […]
17 April, 2019 at 5:09 am
On the universality of the incompressible Euler equation on compact manifolds, II. Non-rigidity of Euler flows – 刘展均工作室
[…] as the Euler equations provided by the “-principle” of Gromov and its variants (as discussed in these recent notes), although in this case the flexibility comes from adding additional dimensions, rather than by […]
9 June, 2022 at 6:49 am
Michele Gorini
Dear Mr. Tao, , we see from the chain rule that
, we see from the chain rule that  is an approximate difference Navier-Stokes-Reynolds flow at U supported on
is an approximate difference Navier-Stokes-Reynolds flow at U supported on  , where»
, where»  and so on. I called the slow variables
and so on. I called the slow variables 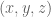 , and the fast ones will be
, and the fast ones will be  .
. , and similar relations. So when I compute the Laplacian, abbreviating
, and similar relations. So when I compute the Laplacian, abbreviating  , I should get
, I should get ![\Delta_{\underline x}v(t,\underline x)=[(\partial_x+N_1\partial_X)^2+(\partial_y+N_1\partial_Y)^2+(\partial_z+N_1\partial_Z)^2]\boldmath v(t,\underline x,\underline X)=[\partial_x^2+2N_1\partial_x\partial_X+N_1^2\partial_X^2+\partial_y^2+2N_1\partial_y\partial_Y+N_1^2\partial_Y^2+\partial_z^2+2N_1\partial_z\partial_Z+N_1^2\partial_Z^2]\boldmath v(t,\underline x,\underline X)=(\Delta_{\underline x}+N_1^2\Delta_{\underline X}+2N_1\nabla_{\underline x}\cdot\nabla_{\underline X}](https://s0.wp.com/latex.php?latex=%5CDelta_%7B%5Cunderline+x%7Dv%28t%2C%5Cunderline+x%29%3D%5B%28%5Cpartial_x%2BN_1%5Cpartial_X%29%5E2%2B%28%5Cpartial_y%2BN_1%5Cpartial_Y%29%5E2%2B%28%5Cpartial_z%2BN_1%5Cpartial_Z%29%5E2%5D%5Cboldmath+v%28t%2C%5Cunderline+x%2C%5Cunderline+X%29%3D%5B%5Cpartial_x%5E2%2B2N_1%5Cpartial_x%5Cpartial_X%2BN_1%5E2%5Cpartial_X%5E2%2B%5Cpartial_y%5E2%2B2N_1%5Cpartial_y%5Cpartial_Y%2BN_1%5E2%5Cpartial_Y%5E2%2B%5Cpartial_z%5E2%2B2N_1%5Cpartial_z%5Cpartial_Z%2BN_1%5E2%5Cpartial_Z%5E2%5D%5Cboldmath+v%28t%2C%5Cunderline+x%2C%5Cunderline+X%29%3D%28%5CDelta_%7B%5Cunderline+x%7D%2BN_1%5E2%5CDelta_%7B%5Cunderline+X%7D%2B2N_1%5Cnabla_%7B%5Cunderline+x%7D%5Ccdot%5Cnabla_%7B%5Cunderline+X%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
. and company.
and company.
I have a small question.
In this post, you say «For any shift
From the chain rule,
However, the equations that define approximate fast-slow solutions do not have any trace of those mixed terms. Am I missing something? Can we say those terms are zero? Otherwise what becomes of them?
PS You have an \eqref[bd-5} which does not render because of that open square bracket, it is around the point where you define
[Corrected (and missing terms reinstated), thanks – T.]