Ben Krause, Mariusz Mirek, and I have uploaded to the arXiv our paper Pointwise ergodic theorems for non-conventional bilinear polynomial averages. This paper is a contribution to the decades-long program of extending the classical ergodic theorems to “non-conventional” ergodic averages. Here, the focus is on pointwise convergence theorems, and in particular looking for extensions of the pointwise ergodic theorem of Birkhoff:
Theorem 1 (Birkhoff ergodic theorem) Letbe a measure-preserving system (by which we mean
is a
-finite measure space, and
is invertible and measure-preserving), and let
for any
. Then the averages
converge pointwise for
-almost every
.
Pointwise ergodic theorems have an inherently harmonic analysis content to them, as they are closely tied to maximal inequalities. For instance, the Birkhoff ergodic theorem is closely tied to the Hardy-Littlewood maximal inequality.
The above theorem was generalized by Bourgain (conceding the endpoint , where pointwise almost everywhere convergence is now known to fail) to polynomial averages:
Theorem 2 (Pointwise ergodic theorem for polynomial averages) Letbe a measure-preserving system, and let
for any
. Let
be a polynomial with integer coefficients. Then the averages
converge pointwise for
-almost every
.
For bilinear averages, we have a separate 1990 result of Bourgain (for functions), extended to other
spaces by Lacey, and with an alternate proof given, by Demeter:
Theorem 3 (Pointwise ergodic theorem for two linear polynomials) Letbe a measure-preserving system with finite measure, and let
,
for some
with
. Then for any integers
, the averages
converge pointwise almost everywhere.
It has been an open question for some time (see e.g., Problem 11 of this survey of Frantzikinakis) to extend this result to other bilinear ergodic averages. In our paper we are able to achieve this in the partially linear case:
Theorem 4 (Pointwise ergodic theorem for one linear and one nonlinear polynomial) Letbe a measure-preserving system, and let
,
for some
with
. Then for any polynomial
of degree
, the averages
converge pointwise almost everywhere.
We actually prove a bit more than this, namely a maximal function estimate and a variational estimate, together with some additional estimates that “break duality” by applying in certain ranges with , but we will not discuss these extensions here. A good model case to keep in mind is when
and
(which is the case we started with). We note that norm convergence for these averages was established much earlier by Furstenberg and Weiss (in the
case at least), and in fact norm convergence for arbitrary polynomial averages is now known thanks to the work of Host-Kra, Leibman, and Walsh.
Our proof of Theorem 4 is much closer in spirit to Theorem 2 than to Theorem 3. The property of the averages shared in common by Theorems 2, 4 is that they have “true complexity zero”, in the sense that they can only be only be large if the functions involved are “major arc” or “profinite”, in that they behave periodically over very long intervals (or like a linear combination of such periodic functions). In contrast, the average in Theorem 3 has “true complexity one”, in the sense that they can also be large if
are “almost periodic” (a linear combination of eigenfunctions, or plane waves), and as such all proofs of the latter theorem have relied (either explicitly or implicitly) on some form of time-frequency analysis. In principle, the true complexity zero property reduces one to study the behaviour of averages on major arcs. However, until recently the available estimates to quantify this true complexity zero property were not strong enough to achieve a good reduction of this form, and even once one was in the major arc setting the bilinear averages in Theorem 4 were still quite complicated, exhibiting a mixture of both continuous and arithmetic aspects, both of which being genuinely bilinear in nature.
After applying standard reductions such as the Calderón transference principle, the key task is to establish a suitably “scale-invariant” maximal (or variational) inequality on the integer shift system (in which with counting measure, and
). A model problem is to establish the maximal inequality
The first step is to understand when the single-scale estimate (2) can come close to equality. A key example to keep in mind is when ,
,
where
is a small modulus,
are such that
,
is a smooth cutoff to an interval
of length
, and
is also supported on
and behaves like a constant on intervals of length
. Then one can check that (barring some unusual cancellation) (2) is basically sharp for this example. A remarkable result of Peluse and Prendiville (generalised to arbitrary nonlinear polynomials
by Peluse) asserts, roughly speaking, that this example basically the only way in which (2) can be saturated, at least when
are supported on a common interval
of length
and are normalised in
rather than
. (Strictly speaking, the above paper of Peluse and Prendiville only says something like this regarding the
factors; the corresponding statement for
was established in a subsequent paper of Peluse and Prendiville.) The argument requires tools from additive combinatorics such as the Gowers uniformity norms, and hinges in particular on the “degree lowering argument” of Peluse and Prendiville, which I discussed in this previous blog post. Crucially for our application, the estimates are very quantitative, with all bounds being polynomial in the ratio between the left and right hand sides of (2) (or more precisely, the
-normalized version of (2)).
For our applications we had to extend the inverse theory of Peluse and Prendiville to an
theory. This turned out to require a certain amount of “sleight of hand”. Firstly, one can dualise the theorem of Peluse and Prendiville to show that the “dual function”
Using these inverse theorems (and the Ionescu-Wainger multiplier theory) one still has to understand the “major arc” portion of (1); a model case arises when are supported near rational numbers
with
for some moderately large
. The inverse theory gives good control (with an exponential decay in
) on individual scales
, and one can leverage this with a Rademacher-Menshov type argument (see e.g., this blog post) and some closer analysis of the bilinear Fourier symbol of
to eventually handle all “small” scales, with
ranging up to say
where
for some small constant
and large constant
. For the “large” scales, it becomes feasible to place all the major arcs simultaneously under a single common denominator
, and then a quantitative version of the Shannon sampling theorem allows one to transfer the problem from the integers
to the locally compact abelian group
. Actually it was conceptually clearer for us to work instead with the adelic integers
, which is the inverse limit of the
. Once one transfers to the adelic integers, the bilinear operators involved split up as tensor products of the “continuous” bilinear operator

17 comments
Comments feed for this article
4 August, 2020 at 1:57 am
qwerty
Theorem 2: did you mean p>1?
[Corrected, thanks – T.]
2 September, 2020 at 7:59 am
IQ news
I believe the author of this blog is a person with a high IQ. I read an article about him with the highest IQ in America.
4 August, 2020 at 12:58 pm
Anonymous
Is the upper bound 3/2 in theorem 3 the best possible ?
7 August, 2020 at 9:49 am
Terence Tao
This question (or its counterpart for the closely related bilinear Hilbert transform) is actually one of the key open problems in time frequency analysis; the standard time-frequency techniques break down past this threshold, but this has not yet led to an actual counterexample to boundedness or convergence beyond this point. See for instance https://arxiv.org/abs/1409.3875 for some attempts to create such counterexamples.
6 August, 2020 at 3:32 am
Anonymous
Should $G(x) = H(x)$ rather than $G(x) = F(x)$ to respect the $N^2$ spatial scale?
[Corrected, thanks – T.]
7 August, 2020 at 1:04 pm
Satan
terence tao Let me attempt to make the path integral rigorous.
you can define the path integral as follows.
you discretize the 3d space and you define a path from point (x,y,z) to point (x’,y’,z’) by adjacent cubes.
for every such discrete path you give it a weight which is as follows:
the number of algorithms which produce this path divided by the total number of algorithms – and taking this limit to infinity, in other words the probability of a random algorithm generator to produce an algorithm which produce this path.
then you sum over all path each multiplied by its weigh, and because you discretized the space you take this infinite sum to the limit of infinity such that in each step the cubes that divide the space are smaller and smaller
7 August, 2020 at 6:38 pm
Asaf
Are there characteristic factors (in the sense of Furstenberg-Weiss) for those types of averages?
Another question – is the convergence result becomes easier when we assume some mixing condition on one system (or both)?
10 August, 2020 at 7:24 pm
Terence Tao
For these averages the characteristic factor is the profinite (or rational Kronecker) factor, i.e., the factor generated by the periodic functions (or the rational spectrum of the shift). This is basically already in the original paper of Furstenberg and Weiss (at least for the quadratic polynomial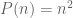 ).
).
Mixing conditions certainly make norm convergence easier, but to my knowledge there is no way to use mixing hypotheses to simplify the proof of pointwise ae convergence for these averages. But there is prior work establishing pointwise convergence for multilinear polynomial averages for exact endomorphisms and K-automorphisms by Derrien and Lesigne (reference [20] in the paper).
7 August, 2020 at 7:09 pm
Mike Jones
Where did you submit this paper?
13 August, 2020 at 4:32 pm
The Ionescu-Wainger multiplier theorem and the adeles | What's new
[…] I’ve just uploaded to the arXiv my paper The Ionescu-Wainger multiplier theorem and the adeles“. This paper revisits a useful multiplier theorem of Ionescu and Wainger on “major arc” Fourier multiplier operators on the integers (or lattices ), and strengthens the bounds while also interpreting it from the viewpoint of the adelic integers (which were also used in my recent paper with Krause and Mirek). […]
16 August, 2020 at 9:59 am
Anonymous
Within the references of the paper uploaded on ArXiv, a minor correction related to the ref #20: Un théorème … Annales de l’Institut Henri Poincaré (IHP)
16 August, 2020 at 10:35 am
Anonymous
Congratulations for your paper.
In order to improve it, within the references of its first version uploaded on the ArXiv plateform, here are very minor corrections and precisions related to :
– the ref #15: … des groupes p-adiques. Bulletin de la Société Mathématique de France (SMF), 89:43-75, Paris, France, 1961.
– the ref #20: Un théorème … Annales de l’Institut Henri Poincaré (IHP) en probabilités et statistiques, 32(6):765-778, Paris, France, 1996.
– the ref #23: for paraproducts. (the final dot is missing)
Kind regards
26 August, 2020 at 10:03 pm
Chen
Just found a typo, in Theorem 2, the second “polynpmial”.
[Corrected, thanks – T.]
2 September, 2020 at 2:03 pm
Huang
Another typo founded: “Fubini’s theorem, Holder’s inequality” => “Fubini’s theorem, Ho¨lder’s inequality”
[Corrected, thanks – T.]
25 April, 2024 at 11:35 am
Anonymous
Hello, professor Tao: I’d like to know more on open question (7) in the paper. Based on the spirit the similarity on the proof of boundedness of bilinear Hilbert transform and bilinear maximal function. Could we expect to use the methods in the paper to establish the bounededness of bilinear Radon transform (or its truncation version):
25 April, 2024 at 3:23 pm
Terence Tao
It’s possible, but not guaranteed. The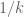 weight potentially generates additional logarithmic divergences in many of the estimates used in our arguments; the question is whether the various gains that we also manage to obtain are sufficiently strong to counteract this divergence. My initial guess is that a naive replication of our arguments will fail to contain these divergences (for instance, the L^p improving inequalities probably fail once such weights are introduced), but it is possible that the argument could somehow be refactored in a way that the logarithmic divergences are only experienced when considering those components of the proof that have really strong additional cancellations. One reason to pursue questions like this is that it may force the person researching these questions to develop a more efficient or simpler proof of our original theorem in order to be able to extend it to the singular setting; I certainly don’t claim that our arguments are the *only* way to proceed for these sorts of questions!
weight potentially generates additional logarithmic divergences in many of the estimates used in our arguments; the question is whether the various gains that we also manage to obtain are sufficiently strong to counteract this divergence. My initial guess is that a naive replication of our arguments will fail to contain these divergences (for instance, the L^p improving inequalities probably fail once such weights are introduced), but it is possible that the argument could somehow be refactored in a way that the logarithmic divergences are only experienced when considering those components of the proof that have really strong additional cancellations. One reason to pursue questions like this is that it may force the person researching these questions to develop a more efficient or simpler proof of our original theorem in order to be able to extend it to the singular setting; I certainly don’t claim that our arguments are the *only* way to proceed for these sorts of questions!
As discussed in the paper, there may be model versions of these questions on other domains than the integers, such as the reals, the p-adics, or the adeles, which may be worth studying first as toy problems that already capture some, but not all, of the main difficulties.
26 April, 2024 at 10:06 am
Anonymous
Thanks for detailed explications!