Asgar Jamneshan and I have just uploaded to the arXiv our paper “Foundational aspects of uncountable measure theory: Gelfand duality, Riesz representation, canonical models, and canonical disintegration“. This paper arose from our longer-term project to systematically develop “uncountable” ergodic theory – ergodic theory in which the groups acting are not required to be countable, the probability spaces one acts on are not required to be standard Borel, or Polish, and the compact groups that arise in the structural theory (e.g., the theory of group extensions) are not required to be separable. One of the motivations of doing this is to allow ergodic theory results to be applied to ultraproducts of finite dynamical systems, which can then hopefully be transferred to establish combinatorial results with good uniformity properties. An instance of this is the uncountable Mackey-Zimmer theorem, discussed in this companion blog post.
In the course of this project, we ran into the obstacle that many foundational results, such as the Riesz representation theorem, often require one or more of these countability hypotheses when encountered in textbooks. Other technical issues also arise in the uncountable setting, such as the need to distinguish the Borel -algebra from the (two different types of) Baire
-algebra. As such we needed to spend some time reviewing and synthesizing the known literature on some foundational results of “uncountable” measure theory, which led to this paper. As such, most of the results of this paper are already in the literature, either explicitly or implicitly, in one form or another (with perhaps the exception of the canonical disintegration, which we discuss below); we view the main contribution of this paper as presenting the results in a coherent and unified fashion. In particular we found that the language of category theory was invaluable in clarifying and organizing all the different results. In subsequent work we (and some other authors) will use the results in this paper for various applications in uncountable ergodic theory.
The foundational results covered in this paper can be divided into a number of subtopics (Gelfand duality, Baire -algebras and Riesz representation, canonical models, and canonical disintegration), which we discuss further below the fold.
— 1. Gelfand duality —
Given a compact Hausdorff space , one can form the space
of continuous functions from
to
; such functions are necessarily bounded and compactly supported, and they form a commutative unital
-algebra. Conversely, given a commutative unital
-algebra
, one can produce the Gelfand spectrum
, which we define here as the collection of unital
-homomorphisms
from
to
. This spectrum can be viewed as a subset of
and inherits a topology from the product topology on that latter space that turns the spectrum into a compact Hausdorff space. The classical Gelfand duality between compact Hausdorff spaces and unital commutative
-algebras asserts that these two operations
and
“essentially invert” each other:
is homeomorphic to
, and
is isomorphic as a commutative unital
-algebra to
. In fact there is a more precise statement: the operations
,
are in fact contravariant functors that form a duality of categories between the category
of compact Hausdorff spaces and the category
of commutative unital
-algebras. This duality of categories asserts, roughly speaking, that the operations
,
and the Gelfand duality isomorphisms interact in the “natural” fashion with respect to morphisms: for instance, any continuous map
between compact Hausdorff spaces induces a commutative unital
-homomorphism
defined by the pullback map
, and similarly any commutative unital
-homomorphism
induces a continuous map
defined by
, and the homeomorphisms between
and
and between
and
commute with the continuous maps
and
in the “natural” fashion. These sorts of properties are routine to verify and mostly consist of expanding out all the definitions.
It is natural to ask what the analogous Gelfand duality is for locally compact Hausdorff spaces. Somewhat confusingly, there appeared to be two such Gelfand dualities in the literature, which appeared at first glance to be incompatible with each other. Eventually we understood that there were two natural categories of locally compact Hausdorff spaces, and dually there were two natural categories of (non-unital) commutative algebras dual to them:
- The category
of locally compact Hausdorff spaces, whose morphisms consist of arbitrary continuous maps between those spaces.
- The subcategory
of locally compact Hausdorff spaces, whose morphisms consist of continuous proper maps between those spaces.
- The category
of commutative
algebras (not necessarily unital), whose morphisms were
homomorphisms
which were non-degenerate in the sense that
is dense in
(this was automatic in the unital case, but now needs to be imposed as an additional hypothesis).
- The larger category
of commutative
algebras (not necessarily unital), whose morphisms were non-degenerate
homomorphisms
into the multiplier algebra
of
. (It is not immediately obvious that one can compose two such morphisms together, but it can be shown that every such homomorphism has a unique extension to a homomorphism from
to
, which can then be used to create a composition law.)
The map that takes a locally compact space to the space of continuous functions that vanish at infinity, together with the previously mentioned Gelfand spectrum map
, then forms a duality of categories between
and
, and between
and
. Furthermore, these dualities of categories interact well with the two standard compactifications of locally compact spaces: the Stone-Cech compactification
, and the Alexandroff compactification
(also known as the one point compactification). From a category theoretic perspective, it is most natural to interpret
as a functor from
to
, and to interpret
as a functor from
to the category
of pointed compact Hausdorff spaces (the notation here is a special case of comma category notation). (Note in particular that a continuous map
between locally compact Hausdorff spaces needs to be proper in order to guarantee a continuous extension
to the Alexandroff compactification, whereas no such properness condition is needed to obtain a continuous extension
to the Stone-Cech compactification.) In our paper, we summarized relationships between these functors (and some other related functors) in the following diagram, which commutes up to natural isomorphisms:

Thus for instance the space of bounded continuous functions on a locally compact Hausdorff space
is naturally isomorphic to the multiplier algebra of
, and the Stone-Cech compactification
is naturally identified with the Gelfand spectrum of
:
Almost every component of the above diagram was already stated somewhere in the literature; our main contribution here is the synthesis of all of these components together into the single unified diagram.
— 2. Baire -algebras and Riesz duality —
Now we add measure theory to Gelfand duality, by introducing -algebras and probability measures on the (locally) compact Hausdorff side of the duality, and by introducing traces on the
-algebra side. Here we run into the issue that there are three natural choices of
-algebra one can assign to a topological space
:
- The Borel
-algebra, generated by the open (or closed) subsets of
.
- The
-Baire
-algebra, generated by the bounded continuous functions on
(equivalently, one can use arbitrary continuous functions on
; these are also precisely the sets whose indicator functions are Baire functions with respect to a countable ordinal).
- The
-Baire
-algebra, generated by the compactly supported continuous functions on
(equivalently, one can use continuous functions on
going to zero at infinity; these are also precisely the sets generated by compact
sets).
For compact Hausdorff spaces, the two types of Baire -algebras agree, but they can diverge for locally compact Hausdorff spaces. Similarly, the Borel and Baire algebras agree for compact metric spaces, but can diverge for more “uncountable” compact Hausdorff spaces. This is most dramatically exemplified by the Nedoma pathology, in which the Borel
-algebra of the Cartesian square
of a locally compact Hausdorff space
need not be equal to the product of the individual Borel
-algebra, in contrast to the Baire
-algebra which reacts well with the product space construction (even when there are uncountably many factors). In particular, the group operations on a locally compact Hausdorff group can fail to be Borel measurable, even though they are always Baire measurable. For these reasons we found it desirable to adopt a “Baire-centric” point of view, in which one prefers to use the Baire
-algebras over the Borel
-algebras in compact Hausdorff or locally compact Hausdorff settings. (However, in Polish spaces it seems Borel
-algebras remain the more natural
-algebra to use.) It turns out that the two Baire
-algebras can be divided up naturally between the two categories
of locally compact Hausdorff spaces, with the
-Baire
-algebra naturally associated to
and the
-algebra naturally associated to
. The situation can be summarized by the following commuting diagram of functors between the various categories of (locally) compact Hausdorff spaces and the category
of concrete measurable spaces (sets equipped with a
-algebra):

To each category of (locally) compact Hausdorff spaces, we can then define an associated category of (locally) compact Hausdorff spaces equipped with a Radon probability measure, where the underlying -algebra is as described above, and “Radon” means “compact
-inner regular”. For instance,
is the category of compact Hausdorff spaces equipped with a Baire probability measure
with the inner regularity property

Again, each component of this diagram was essentially already in the literature in either explicit or implicit form. In the paper we also review the Riesz representation theory for traces on rather than
, in which an additional “
-smoothness” property is needed in order to recover a Radon probability measure on
. The distinction between Baire and Borel
-algebras ends up being largely elided in the Riesz representation theory, as it turns out that every Baire-Radon probability measure (using either of the two Baire algebras) on a locally compact Hausdorff has a unique extension to a Borel-Radon probability measure (where for Borel measures, the Radon property is now interpreted as “compact inner regular” rather than “compact
inner regular”).
— 3. The canonical model of opposite probability algebras —
Given a concrete probability space – a set
equipped with a
-algebra
and a probability measure
– one can form the associated probability algebra
by quotienting the
-algebra
by the null ideal
and then similarly quotienting the measure
to obtain an abstract countably additive probability measure
. More generally, one can consider abstract probability algebras
where
is a
-complete Boolean algebra and
is a countably additive probability measure with the property that
whenever
. This gives a category
. Actually to align things closer to the category of concrete probability spaces
, it is better to work with the opposite category
of opposite probability algebras
where the directions of the morphisms are reversed.
Many problems and concepts in ergodic theory are best phrased “up to null sets”, which can be interpreted category-theoretically by applying a suitable functor from a concrete category such as to the opposite probability algebra category
to remove all the null sets. However, it is sometimes convenient to reverse this process and model an opposite probability algebra by a more concrete probability space, and to also model morphisms
between opposite probability algebras (
-complete Boolean homomorphisms from
to
that preserve measure) by concrete maps. Ideally the model spaces should also be compact Hausdorff spaces, and the model morphisms continuous maps, so that methods from topological dynamics may be applied. There are various ad hoc ways to create such models in “countable” settings, but it turns out that there is a canonical and “universal” model
of any opposite probability algebra
that one can construct in a completely functorial setting (so that any dynamics on the opposite probability algebra
automatically carry over to concrete dynamics on
). The quickest way to define this model is by the formula
- (Topological structure)
is a compact Hausdorff space. In fact it is a Stone space with the additional property that every Baire-measurable set is equal to a clopen set modulo a Baire-meager set (such spaces we call
-spaces in our paper). Furthermore a Baire set is null if and only if it is meager. Any opposite probability algebra morphism
gives rise (in a functorial fashion) to a surjective continuous map
with the additional property that the inverse image of Baire-meager sets are Baire-meager. Furthermore, one has the (somewhat surprising) “strong Lusin property”: every element of
has a unique representative in
(thus, every bounded measurable function on
is equal almost everywhere to a unique continuous function).
- (Concrete model) The opposite probability algebra of
is (naturally) isomorphic to
.
- (Universality) There is a natural inclusion (in the category
of abstract probability spaces) from
(which is
interpreted in
) into
, which is universal amongst all inclusions of
into compact Hausdorff probability spaces.
- (Canonical extension) Every abstractly measurable map from
to a compact Hausdorff space
has a unique extension to a continuous map from
to
.
This canonical model seems quite analogous to the Stone-Cech compactification
. For instance the analogue of the canonical extension property for
is that every continuous map from a locally compact space
to a compact Hausdorff space
has a unique extension to a continuous map from
to
. In both cases the model produced is usually too “large” to be separable, so this is a tool that is only available in “uncountable” frameworks.
There is an alternate description of the canonical model, which is basically due to Fremlin, and is based on Stone-type dualities rather than Riesz type dualities. Namely, one starts with the -complete Boolean algebra attached to the opposite probability space
, and constructs its Stone dual, which is a
space. Every Baire set in this space is equal modulo Baire-meager sets to a clopen set, which by Stone duality is identifiable with an element of the probability algebra. The measure on
then induces a measure on the
-space, and this compact Hausdorff probability space can serve as the canonical model
. The functoriality of this construction is closely tied to the functoriality of the Loomis-Sikorski theorem (discussed in this previous blog post). The precise connection in terms of functors and categories is a little complicated to describe, though, as the following diagram indicates:

One quick use of the canonical model is that it allows one to perform a variety of constructions on opposite probability algebras by passing to the canonical model and performing the analogous operation there. For instance, if one wants to construct a product of some number of opposite probability algebras, one can first take the product
of the concrete models (as a compact Hausdorff probability space), then extract the opposite probability algebra of that space. We will similarly use this model to construct group skew-products and homogeneous skew-products in a later paper.
— 4. Canonical disintegration —
Given a probability space and a probability-preserving factor map
from
to another probability space
, it is often convenient to look for a disintegration of
into fibre measures
with the property that the conditional expectation
of a function
(defined as the orthogonal projection in
to
, viewed as a subspace in
) is given pointwise almost everywhere by
Among other things, the canonical disintegration makes it easy to construct relative products of opposite probability algebras, and we believe it will also be of use in developing uncountable versions of Host-Kra structure theory.

37 comments
Comments feed for this article
4 October, 2020 at 5:32 pm
Allen Knutson
I was briefly worried that in your categorical account you’d avoided the term “adjoint functor”. I was glad to see that it’s used in the actual paper (even if probably not enough times).
7 October, 2020 at 3:41 pm
Terence Tao
Yeah, the Stone-Cech compactification, canonical model, and Loomis-Sikorski functors are all left-adjoint to “forgetful functors” (or more precisely “casting functors”, since one can quibble as to whether actions such as passing from concrete to point-free frameworks and then quotienting out null sets counts as “forgetting structure”). In particular this deepens the analogy between the canonical model and the Stone-Cech compactification. I could imagine that some of the other universality properties of the canonical model that we list are simply abstract nonsense consequences of this adjunction, but in any case we found it instructive to work them out in a more pedestrian fashion.
4 October, 2020 at 5:56 pm
Edgawliet
This is so heavy.
5 October, 2020 at 12:31 am
David Roberts
It is a neat result that a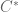 -algebra always admits a second topology (in addition to the Banach topology), the *strict* topology, and that the underlying vector space of the multiplier algebra is the completion in this topology. Even better, the two vector space topologies are compatible, making what Cooper calls a “Saks space”, and the multiplier algbra is the Saks space completion. Cooper also defined (commutative) *Saks algebras*, and commutative
-algebra always admits a second topology (in addition to the Banach topology), the *strict* topology, and that the underlying vector space of the multiplier algebra is the completion in this topology. Even better, the two vector space topologies are compatible, making what Cooper calls a “Saks space”, and the multiplier algbra is the Saks space completion. Cooper also defined (commutative) *Saks algebras*, and commutative 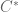 -algebras give rise to these in this way, and then the multiplier algebra is the Saks *algebra* completion. This is (as one could expect, a functorial operation. All of this is in the commutative case; the non-commutative case has not been treated, but it is on my long wish-list of things to do, if anyone else finds such a thing interesting.
-algebras give rise to these in this way, and then the multiplier algebra is the Saks *algebra* completion. This is (as one could expect, a functorial operation. All of this is in the commutative case; the non-commutative case has not been treated, but it is on my long wish-list of things to do, if anyone else finds such a thing interesting.
The functor from commutative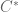 -algebras to complete (commutative) Saks algebras is what is known as a “relative monad”, and the “larger category” of
-algebras to complete (commutative) Saks algebras is what is known as a “relative monad”, and the “larger category” of 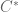 -algebras with the more interesting morphisms is the Kleisli category of this relative monad. So the construction of this larger category is in some sense quite formal, since an analogue of the strict topology can be defined on any topological (
-algebras with the more interesting morphisms is the Kleisli category of this relative monad. So the construction of this larger category is in some sense quite formal, since an analogue of the strict topology can be defined on any topological ( )-algebra, in a canonical way.
)-algebra, in a canonical way.
5 October, 2020 at 7:29 am
fb
I think there is a misspell of the author in the Maths Reviews link : it is actually V. A. Rokhlin instead of V. A. Rohlin if I am not mistaken
(see : http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=sm&paperid=5995&option_lang=eng)
[Thanks, this will be corrected in the next revision of the ms. -T]
5 October, 2020 at 11:38 am
Dmitri
The claim about the misspelling is incorrect: the article itself spells it as Rohlin, not Rokhlin. See the scanned PDF file here: https://web.archive.org/web/20150722004152/http://ma.huji.ac.il/~matang02/rohlin.pdf
5 October, 2020 at 11:51 am
fb
I do not think; the author is :
https://en.wikipedia.org/wiki/Vladimir_Abramovich_Rokhlin
5 October, 2020 at 9:29 am
Anonymous
Are these foundational results based on assuming the standard ZFC set theory?
5 October, 2020 at 10:31 am
Terence Tao
Yes, we work in ZFC, and in particular assume the axiom of choice; several Hahn-Banach type extension theorems are implicitly used in order to affirm various dualities such as Stone duality or Gelfand duality. Certainly the Stone-Cech compactification cannot be constructed with the desired properties without the axiom of choice (possibly one might be able to get away with something slightly weaker such as the ultrafilter lemma, but I am not an expert on these subtleties).
5 October, 2020 at 9:39 am
novac
Dear Professor
French typos founded in the last reference of your extraordinary paper [50] (Weil, 1937):
– a structure —-> à structure
– sure la topologie —–> sur la topologie
Your sincerely
[Thanks, this will be corrected in the next version of the ms. -T]
5 October, 2020 at 10:33 am
Chen
A minor typo p. 2 : “aforementioned” instead of “above-mentioned”.
[This will be changed in the next revision of the ms – T.]
5 October, 2020 at 1:37 pm
Anonymous
How is this a typo
5 October, 2020 at 4:11 pm
Mark Lewko
Could you say a bit about the potential combinatorial implications/applications of the longer term program?
6 October, 2020 at 7:40 am
Terence Tao
One of our primary goals is to be able to establish the inverse conjecture for the Gowers norm and the Host-Kra structure theorem for measure-preserving systems in a unified fashion, as if one takes an “ultraproduct” of the former one gets something that resembles an “uncountable” version of the latter. (The Camarena-Szegedy and Candela-Szegedy proof of the former proceeds somewhat along these lines but falls short of recovering the entirety of the Host-Kra theory.) We also expect this approach to give a strengthened version of the inverse conjecture that has more uniformity properties with respect to the underlying group (or approximate group) with respect to which one is computing the Gowers norm.
A bit more speculatively, once we have a completely rigorous way to transfer back and forth between additive combinatorics and ergodic theory (beyond the existing Furstenberg correspondence principle, which comes close to, but does not quite manage, to connect the Gowers type theory to the Host-Kra type theory), one could hope to be able to directly apply other deep results in ergodic theory to additive combinatorial settings (as opposed to merely reasoning by analogy, which is basically the current state of affairs). For instance the theory of joinings is a basic tool in ergodic theory which so far has only made a very modest appearance in additive combinatorics.
6 October, 2020 at 11:08 am
Anonymous
In other words, this program may have the potential to unify several mathematical branches by creating correspondences (or “bridges”) among them.
5 October, 2020 at 5:04 pm
David Roberts
On a style point, definition A.1 is inconsistent with the other usage. “A category Cat is a class of objects (which we refer to as Cat-objects),” conflicts with the long-standing convention in category theory to have “Cat” reserved to refer to the category of (small, say) categories. Saying instead “A category C is a class of objects (which we refer to as C-objects),” will then make more sense. Now C is a placeholder, and the following examples are the cases C=Set and C=Grp. The same is true for Definition A.4 and all the surrounding discussion. And for A.13 etc. It’s even worse there, since functors are the morphisms in Cat, so writing a generic functor as , where this is now a morphism in the category of categories, is really, really grating. And it continues. This not a good look.
, where this is now a morphism in the category of categories, is really, really grating. And it continues. This not a good look.
This feels like what I imagine it would feel like to a harmonic analysist if a category theorist invented their own notation for objects in analysis that conflicts with decades of established notation. Imagine someone deciding was a good notation for the space of continuous functions, because they preserve limits…).
was a good notation for the space of continuous functions, because they preserve limits…).
[Good point, this will be changed in the next revision of the ms (fortunately it amounted to changing one line of LaTeX code) -T.]
5 October, 2020 at 5:24 pm
LonYing
What an incredible paper!!!
In the bibliography the ref #27 should be yet completed by ‘arXiv:2010.00574 (2020).’ instead of ‘Preprint.’
Best regards and congratulations for your contribution
[Thanks, this will be corrected in the next revision of the ms. -T]
5 October, 2020 at 5:46 pm
Karl
Concerning the ref [50] if a previous post has already pointed out typos in the title, it should be nevertheless corrected as follows: “Publications de l’Institut Mathématique de l’Université de Strasbourg, Vol. 551, Strasbourg, France, (1938).” instead of “Actualités … (1937).”
[Thanks, this will be corrected in the next revision of the MS. -T]
5 October, 2020 at 6:09 pm
Mike
in the ref #44 ‘Band’ (in German) ‘Issue’ (in English) if you want to be explicit
6 October, 2020 at 3:15 pm
Zhao
In my opinion the preceeding post, which is not very clear, means that if you want to be more explicit for non German readers you should replace in the ref [44] the term “Band” by the term “Issue”.
Kind regards
6 October, 2020 at 4:48 pm
LeBron
Dear Pr. Dr. Tao,
In order to be exhaustive, you could add in the bibliography the second corresponding reference of Hewitt & Ross entitled “Abstract Harmonic Analysis. Volume II. …. Springer Verlag”.
7 October, 2020 at 3:48 am
Oliver Knill
I always had been under the impression that what you can do with countable group actions in ergodic theory can be done in the uncountable case too. There are mechanisms in classical ergodic theory like time one maps or Poincare return maps for example which allow to reduce flows to maps. Also for groups which are inverse limits of groups like p-adic integers one could expect the limit to behave nicely. Also extension of the Mackey Zimmer theorem mentioned in the previous blog entry to the uncountable case confirms also that there is not much new. As a motivation for this part of ergodic theory it would be good to have a concrete example of an uncountable group action on a probability space, where a new ergodic phenomenon happens. The motivation from combinatorics has been mentioned already, but one can suspect that these combinatorial results can be attacked also by traditional ergodic theory of countable group actions once one knows how to do it.
7 October, 2020 at 11:26 am
Terence Tao
What seems to be emerging from our investigations is that uncountable ergodic theory closely resembles countable ergodic theory *when set up correctly*, but if one sets things up naively one often runs into pathological counterexamples. For instance, there are various representation theorems (e.g., Maharam-von Neumann) for actions of countable groups that roughly speaking allow an abstract action of a countable group on a complete probability space to be modeled by a concrete action on the same space which agrees almost everywhere with the abstract action. But this fails in the uncountable setting, and not just of “pathological” examples: there is a result of Glasner, Tsirelson, and Weiss that shows that a very natural uncountable group, namely the automorphism group of Gaussian measure, does not act in pointwise fashion on the natural probability space supporting that Gaussian measure. On the other hand, the canonical model given in our paper does give such a pointwise action that is even continuous. The catch is that this action is not on the original probability space, but rather on the Stone space of the underlying probability algebra, which is still compact but is otherwise rather large (in particular, it is not separable or metrisable). Nevertheless this seems to be the “right” concrete model to use in uncountable ergodic theory (we rely on it extensively to prove the uncountable Mackey-Zimmer theorem, for instance).
In a similar fashion, when working with cocycles taking values in inseparable compact groups we initially assumed naively that we should use the Borel sigma algebra on these groups to perform our analysis, but very quickly ran into the Nedoma pathology, which among other things shows that the group options can fail to be Borel measurable, causing huge difficulties. However if one sets up the entire theory using Baire sigma algebras instead of Borel sigma algebras then everything works very nicely, just as in the separable case. (Initially this caused some concern for us because Haar measure is usually defined on the Borel sigma algebra rather than the Baire sigma algebra, but in fact it can be defined on either, with both being equally canonical, because every Baire-Radon probability measure turns out to have a unique Borel-Radon extension.) While these subtleties are perhaps just technicalities, they were somewhat surprising at least to us, and I think the careful untangling of these issues has been edifying (for instance the revelation for us that there were two distinct categories of locally compact Hausdorff spaces which divvied up between them all the various analytic structures of such spaces greatly clarified for us the rather confusing functorial status of basic operations such as the Alexandroff and Stone-Cech compactifications).
7 October, 2020 at 1:55 pm
David Roberts
“The catch is that this action is not on the original probability space, but rather on the Stone space of the underlying probability algebra, which is still compact but is otherwise rather large (in particular, it is not separable or metrisable).”
This makes me vaguely think that looking at locales might be worthwhile. See for instance discussion at this blog post: https://projects.lsv.ens-cachan.fr/topology/?page_id=1597
7 October, 2020 at 3:11 pm
Terence Tao
Yeah, locales are pretty close in spirit to the categories studied here: we play with concrete topological spaces, concrete measurable spaces, and abstract measurable spaces, but we don’t attempt to describe abstract topological spaces, which is what locales are best suited for. One could in particular imagine a completely abstract Riesz representation theorem on certain locales (maybe such a theorem already exists in the literature).
If one restricts attention to *measurable* locales then one arrives at a category that contains our category of opposite probability algebras (once the actual probability measure is forgotten). There is a Stone and “von Neumann” duality of categories between (measurable) locales and either hyperstonean spaces or commutative von Neumann algebras (not equipped with a trace) that was worked out recently by Pavlov. These could be useful if one wished to extend the Riesz representation theorems in this paper to other localizable spaces (and indeed there are already some Riesz representation theorems at this level of generality). We discuss this a bit in Remark 9.3 of the current paper.
7 October, 2020 at 1:00 pm
Asgar Jamneshan
In a forthcoming paper, P. Durcik, R. Greendfeld, A. Iseli and J. Madrid and myself establish an uncountable version of the amenable ergodic Roth theorem of Bergelson, McCutcheon and Zhang, and by using ultraproducts we can derive from this extension that the set of multiple recurrence times of Roth type is uniformly syndetic over a whole class of systems where the acting groups can be taken from a uniformly amenable set of groups. (As was mentioned previously, taking ultraproducts naturally leads to uncountable systems, even for finite systems). As a special case, we obtain a uniform syndeticity result for a class of countable systems with a single uniformly amenable group (e.g., the integers) acting. It is not immediately obvious to us how one could deduce such a combinatorial uniformity result from an ergodic theory for countable group actions.
7 October, 2020 at 4:47 am
.
Is there any relation to Voevodsky’s category theory work on probability?
7 October, 2020 at 11:51 am
Terence Tao
From what I understand of Voevodsky’s theory, he is working with a category of measurable spaces, in which the morphisms are probability kernels rather than measurable functions. That’s certainly an interesting category (for instance, it is the natural category with which to study Markov processes, which seems to be a key focus of Voevodsky’s work) but we do not use it in this current paper.
7 October, 2020 at 12:52 pm
.
A second question would be the following natural one. Would this new formulation have any relevance to quantum mechanics where probabilities can be given a complex interpretation?
7 October, 2020 at 1:04 pm
Terence Tao
Presumably the framework to consider quantum mechanics would be noncommutative probability, which in our formulation amounts to replacing the category of commutative tracial von Neumann algebras by the category of arbitrary tracial von Neumann algebras. One can also consider noncommutative topology (by similarly removing the requirement of commutativity on the various categories of C^* algebras here). There does seem to be a small amount of literature on, say, noncommutative Riesz representation theorems (e.g., this paper) but it does not seem to be an extensively explored subject currently.
On the other hand it’s not clear to me what the noncommutative analogues of the various dualities in this paper (Gelfand duality, Riesz duality, probability duality, Stone duality) are – it’s reasonably obvious in all the cases what the noncommutative object is on the “algebra” side (one simply removes the requirement that the algebra be commutative), but it’s less clear what is happening on the “physical space” side. For instance, how should one define a “noncommutative compact Hausdorff space”, other than as “an opposite object to a unital C^* algebra”?
7 October, 2020 at 2:23 pm
.
Sorry for making my question unclear. All probability models that apply to qm seem to be countable. When we say superposition of states this would mean there is a necessity to invoke uncountable models and thus would the new framework provide anything new to qm?
7 October, 2020 at 3:18 pm
Terence Tao
I could potentially imagine that certain quantum field theories (as well as several putative quantum gravity theories) might require an inseparable Hilbert space to model them properly, but generally speaking the mathematical foundational issues with such theories are far more severe than just the separable/inseparable distinction, to the point that the inseparability of the Hilbert space is the least of one’s mathematical concerns with such theories. Physically, of course, one can only ever make a finite number of observations, let alone a countable or uncountable number, so I would imagine that it would be difficult to establish physically meaningful distinctions between countable and uncountable quantum mechanics (though perhaps there are subtleties, in the spirit for instance of the recent negative solution to the Connes embedding problem). The quote of Richard Hamming on an analogous question is perhaps apropos: “Does anyone believe that the difference between the Lebesgue and Riemann integrals can have physical significance, and that whether say, an airplane would or would not fly could depend on this difference? If such were claimed, I should not care to fly in that plane.”
7 October, 2020 at 8:21 pm
.
I guess from an ‘applicable’ view point there isn’t much. I would also imagine the mathematician’s job is also not to make planes. However.the engineer’s job is not to fly planes either does not preclude the engineer from not knowing the engineering of flight and contribute to making planes.
17 October, 2020 at 1:59 pm
.
Sorry but does countability have anything to do with quantumness of this universe? Do uncountable models have any roles?
[See my previous answer from Oct 7. -T]
7 October, 2020 at 4:28 pm
Xinhua
Dear Professor
In the noncommutative case could you use the framework of quaternions in your different new models?
8 October, 2020 at 11:37 am
Pablo
Is there a connexion of your work with the recent paper of Gilles Pisier on C* algebras uploaded to ArXiv last August?
6 December, 2021 at 7:39 am
The structure of arbitrary Conze-Lesigne systems | What's new
[…] There is an additional technical issue worth pointing out here (which unfortunately was glossed over in some previous work in the area). Because the cocycle equation (1) and the Conze-Lesigne equation (3) are only valid almost everywhere instead of everywhere, the action of on is technically only a near-action rather than a genuine action, and as such one cannot directly define to be the stabiliser of a point without running into multiple problems. To fix this, one has to pass to a topological model of in which the action becomes continuous, and the stabilizer becomes well defined, although one then has to work a little more to check that the action is still transitive. This can be done via Gelfand duality; we proceed using a mixture of a construction from this book of Host and Kra, and the machinery in this recent paper of Asgar and myself. […]