Rachel Greenfeld and I have just uploaded to the arXiv our paper “The structure of translational tilings in “. This paper studies the tilings
of a finite tile
in a standard lattice
, that is to say sets
(which we call tiling sets) such that every element of
lies in exactly one of the translates
of
. We also consider more general tilings of level
for a natural number
(several of our results consider an even more general setting in which
is periodic but allowed to be non-constant).
In many cases the tiling set will be periodic (by which we mean translation invariant with respect to some lattice (a finite index subgroup) of
). For instance one simple example of a tiling is when
is the unit square
and
is the lattice
. However one can modify some tilings to make them less periodic. For instance, keeping
one also has the tiling set
The most well known conjecture in this area is the Periodic Tiling Conjecture:
Conjecture 1 (Periodic tiling conjecture) If a finite tilehas at least one tiling set, then it has a tiling set which is periodic.
This conjecture was stated explicitly by Lagarias and Wang, and also appears implicitly in this text of Grunbaum and Shepard. In one dimension there is a simple pigeonhole principle argument of Newman that shows that all tiling sets are in fact periodic, which certainly implies the periodic tiling conjecture in this case. The
case was settled more recently by Bhattacharya, but the higher dimensional cases
remain open in general.
We are able to obtain a new proof of Bhattacharya’s result that also gives some quantitative bounds on the periodic tiling set, which are polynomial in the diameter of the set if the cardinality of the tile is bounded:
Theorem 2 (Quantitative periodic tiling in) If a finite tile
has at least one tiling set, then it has a tiling set which is
-periodic for some
.
Among other things, this shows that the problem of deciding whether a given subset of of bounded cardinality tiles
or not is in the NP complexity class with respect to the diameter
. (Even the decidability of this problem was not known until the result of Bhattacharya.)
We also have a closely related structural theorem:
Theorem 3 (Quantitative weakly periodic tiling in) Every tiling set of a finite tile
is weakly periodic. In fact, the tiling set is the union of at most
disjoint sets, each of which is periodic in a direction of magnitude
.
We also have a new bound for the periodicity of tilings in :
Theorem 4 (Universal period for tilings in) Let
be finite, and normalized so that
. Then every tiling set of
is
-periodic, where
is the least common multiple of all primes up to
, and
is the least common multiple of the magnitudes
of all
.
We remark that the current best complexity bound of determining whether a subset of tiles
or not is
, due to Biro. It may be that the results in this paper can improve upon this bound, at least for tiles of bounded cardinality.
On the other hand, we discovered a genuine difference between level one tiling and higher level tiling, by locating a counterexample to the higher level analogue of (the qualitative version of) Theorem 3:
Theorem 5 (Counterexample) There exists an eight-element subsetand a level
tiling
such that
is not weakly periodic.
We do not know if there is a corresponding counterexample to the higher level periodic tiling conjecture (that if tiles
at level
, then there is a periodic tiling at the same level
). Note that it is important to keep the level fixed, since one trivially always has a periodic tiling at level
from the identity
.
The methods of Bhattacharya used the language of ergodic theory. Our investigations also originally used ergodic-theoretic and Fourier-analytic techniques, but we ultimately found combinatorial methods to be more effective in this problem (and in particular led to quite strong quantitative bounds). The engine powering all of our results is the following remarkable fact, valid in all dimensions:
Lemma 6 (Dilation lemma) Suppose thatis a tiling of a finite tile
. Then
is also a tiling of the dilated tile
for any
coprime to
, where
is the least common multiple of all the primes up to
.
Versions of this dilation lemma have previously appeared in work of Tijdeman and of Bhattacharya. We sketch a proof here. By the fundamental theorem of arithmetic and iteration it suffices to establish the case where is a prime
. We need to show that
. It suffices to show the claim
, since both sides take values in
. The convolution algebra
(or group algebra) of finitely supported functions from
to
is a commutative algebra of characteristic
, so we have the Frobenius identity
for any
. As a consequence we see that
. The claim now follows by convolving the identity
by
further copies of
.
In our paper we actually establish a more general version of the dilation lemma that can handle tilings of higher level or of a periodic set, and this stronger version is useful to get the best quantitative results, but for simplicity we focus attention just on the above simple special case of the dilation lemma.
By averaging over all in an arithmetic progression, one already gets a useful structural theorem for tilings in any dimension, which appears to be new despite being an easy consequence of Lemma 6:
Corollary 7 (Structure theorem for tilings) Suppose thatis a tiling of a finite tile
, where we normalize
. Then we have a decomposition
where each
is a function that is periodic in the direction
, where
is the least common multiple of all the primes up to
.
Proof: From Lemma 6 we have for any
, where
is the Kronecker delta at
. Now average over
(extracting a weak limit or generalised limit as necessary) to obtain the conclusion.
The identity (1) turns out to impose a lot of constraints on the functions , particularly in one and two dimensions. On one hand, one can work modulo
to eliminate the
and
terms to obtain the equation
For level tilings the analogue of (2) becomes
We are currently studying what this machinery can tell us about tilings in higher dimensions, focusing initially on the three-dimensional case.

18 comments
Comments feed for this article
8 October, 2020 at 12:03 pm
Chris
A first typo just founded in the ref [HN] : “Caractérisation” instead of “Caracterisation”.
[This will be corrected in the next revision of the ms -T.]
8 October, 2020 at 1:16 pm
Anonymous
Is there any known complete(!) classification of “tiling types” (in addition to translational tiling) in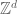 ?
?
8 October, 2020 at 3:26 pm
Hansen
On the blog in the proof of corollary 7 the word ‘function’ may be omitted after ‘Kronecker delta’ i.e. ‘Kronecker delta at’ ===> ‘Kronecker delta function at’.
8 October, 2020 at 3:37 pm
Luis
In the paragraph of the blog located between Theorem 2 and Theorem 3, “Even” –>> “Even if”
[This is not the intended meaning. -T]
8 October, 2020 at 9:50 pm
Anonymous
Who are you to correct him? You (and presumably all your aliases above) obviously don’t know about the subject or the English language. Most of your suggestions are nonsense.
9 October, 2020 at 12:41 am
domotorp
I wanted to suggest to change “in the sense that is the disjoint union” -> “in the sense that IT is the disjoint union”, but now I’m not sure I still dare…
[Corrected, thanks – T.]
8 October, 2020 at 8:15 pm
Raphael
In the preprint 2 sentesec before Remark 1.2 “implies that the problem of determine whether a tile F tiles Zd or not is decidable.”
[Thanks, this will be corrected in the next revision of the ms. -T]
9 October, 2020 at 12:45 am
domotorp
As you note in the preprint, you do not allow rotations. Could any of these methods work if you do? AFAIK, the discrete Einstein problem is still open.
9 October, 2020 at 7:10 am
Terence Tao
In the discrete setting, every tile only has a finite number of rotational copies of it that stay in the lattice, and so tiling with one tile by both translations and rotations is a special case of tiling by translation (i.e., by [orientation-preserving] rigid motions) using more than one (but only finitely many) tiles. For the more general question of translational tiling by a finite set of tiles the tiling problem becomes quite nasty – tilings no longer need to be periodic, and in fact there are tile sets for which the question of whether a tiling exists is in fact undecidable (a result of Berger). However, in these constructions the tile set does not consist simply of rotations of a single tile, so the decidability or periodisability of rigid motion tilings remains open. It seems unlikely to me that the dilation lemma continues to hold if rotations are permitted, and this lemma is critical to our approach, so I don’t think our methods give any positive results towards tiling by rigid motions. Still, the Berger-type constructions hint that such tilings could be significantly less well-behaved than translational tilings.
9 October, 2020 at 6:50 pm
Dan Asimov
In the phrase “discrete einstein problem” the word “einstein” should be lowercased, since it refers literally to “one stone” and not to a person.
9 October, 2020 at 8:12 am
Craig
If I’m not mistaken, one of the two components in your second tiling set example needs a “+1” added to the y coordinate. Otherwise you never cover the odd-y elements of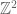 .
.
[Corrected, thanks – T.]
9 October, 2020 at 8:16 am
Sabino Lamonaca
I have never had to deal with such difficult topics.
19 August, 2021 at 7:35 am
Undecidable translational tilings with only two tiles, or one nonabelian tile | What's new
[…] conjecture is known in two dimensions (by work of Bhattacharya when , and more recently by us when ), but remains open in higher dimensions. By the preceding discussion, the conjecture implies […]
3 March, 2022 at 8:34 pm
Measurable tilings by abelian group actions | What's new
[…] my preprint “Measurable tilings by abelian group actions“. This paper is related to an earlier paper of Rachel Greenfeld and myself concerning tilings of lattices , but now we consider the more general situation of tiling a measure […]
4 March, 2022 at 2:00 pm
Anonymous
Is there any heuristic “justification” for conjecture 1?
4 March, 2022 at 3:13 pm
Terence Tao
I think there is an informal intuition that it is “easier” to tile space periodically than it is to tile aperiodically, especially if one does not simply “cheat” by starting with a periodic tiling and “sliding” some of the tiles in it to make it technically aperiodic. The discovery in the 1960s that aperiodic sets of tiles exist at all was considered surprising at the time, but all constructions seemed to require far more than one single tile. An aperiodic tiling also needs a quite extreme level of coordination between the Fourier transform of
also needs a quite extreme level of coordination between the Fourier transform of  and the (distributional) Fourier transform of
and the (distributional) Fourier transform of 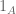 , in particular the latter needs to be supported in the zero set of the former (together with the origin). This hints at an additional difficulty in constructing a single aperiodic tile, as opposed to aperiodic sets of multiple tiles where the Fourier transforms seem to be far less constrained. (This is also related to the dilation lemma being available for tilings by one tile, but not by multiple tiles.)
, in particular the latter needs to be supported in the zero set of the former (together with the origin). This hints at an additional difficulty in constructing a single aperiodic tile, as opposed to aperiodic sets of multiple tiles where the Fourier transforms seem to be far less constrained. (This is also related to the dilation lemma being available for tilings by one tile, but not by multiple tiles.)
19 September, 2022 at 7:31 pm
A counterexample to the periodic tiling conjecture | What's new
[…] (as first observed by Newman), and was proven for by Bhattacharya (with a new proof given by Greenfeld and myself). The continuous periodic tiling conjecture was established for by Lagarias and Wang. By an old […]
19 September, 2022 at 10:22 pm
A counterexample to the periodic tiling conjecture - Veja Online
[…] (as first noticed by Newman), and was confirmed for by Bhattacharya (with a brand new proof given by Greenfeld and myself). The continual periodic tiling conjecture was established for by Lagarias and Wang. By an […]