I was asked the following interesting question from a bright high school student I am working with, to which I did not immediately know the answer:
Question 1 Does there exist a smooth functionwhich is not real analytic, but such that all the differences
are real analytic for every
?
The hypothesis implies that the Newton quotients are real analytic for every
. If analyticity was preserved by smooth limits, this would imply that
is real analytic, which would make
real analytic. However, we are not assuming any uniformity in the analyticity of the Newton quotients, so this simple argument does not seem to resolve the question immediately.
In the case that is periodic, say periodic with period
, one can answer the question in the negative by Fourier series. Perform a Fourier expansion
. If
is not real analytic, then there is a sequence
going to infinity such that
as
. From the Borel-Cantelli lemma one can then find a real number
such that
(say) for infinitely many
, hence
for infinitely many
. Thus the Fourier coefficients of
do not decay exponentially and hence this function is not analytic, a contradiction.
I was not able to quickly resolve the non-periodic case, but I thought perhaps this might be a good problem to crowdsource, so I invite readers to contribute their thoughts on this problem here. In the spirit of the polymath projects, I would encourage comments that contain thoughts that fall short of a complete solution, in the event that some other reader may be able to take the thought further.

33 comments
Comments feed for this article
4 May, 2021 at 1:58 pm
Is there a non-analytic function with all differences analytic? – Mathematics, for all Mankind!
[…] Is there a non-analytic function with all differences analytic? […]
4 May, 2021 at 2:16 pm
Real-user
Hi,
This is a very interesting question. What about posting it in math.stackexchange, or mathoverflow?
4 May, 2021 at 6:03 pm
sylvainjulien
Maybe a detour via algebraic geometry considering germs of real analytic functions could work? I’m also thinking of drawing a parallel with differential geometry viewing the map that maps f to its finite Newtion quotient of parameter h as an analogue of a tangent vector, and the real analyticity of f emerging as a result of the existence of a connexion.
4 May, 2021 at 6:37 pm
Lior Silberman
Let be as given in the problem. Suppose we could find an analytic function
be as given in the problem. Suppose we could find an analytic function  so that
so that 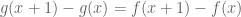 . Then
. Then 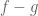 would be a periodic function with analytic difference quotients, hence analytic by the solution above and it would follow that
would be a periodic function with analytic difference quotients, hence analytic by the solution above and it would follow that  is analytic as well.
is analytic as well.
It thus suffices to solve the following problem: given a real analytic function satisfying an appropriate hypothesis find an analytic function
satisfying an appropriate hypothesis find an analytic function  so that
so that  .
.
For a flavour of the hypothesis note that if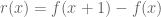 and
and  is integrable then
is integrable then  vanishes on the integers, and
vanishes on the integers, and  is continuous so might possibly have an inverse Fourier transform.
is continuous so might possibly have an inverse Fourier transform.
4 May, 2021 at 8:00 pm
Xiaowei Xu
Maybe this is too elementary and I am sure you have considered this. But we could have worked with the telescoping sum
Then we have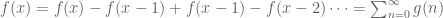 . By the hypothesis, each
. By the hypothesis, each 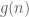 is analytic and have the radius of convergence in an open set of the form
is analytic and have the radius of convergence in an open set of the form 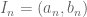 . Thus we just need some type of Baire-Category theorem to ensure that
. Thus we just need some type of Baire-Category theorem to ensure that  . Since
. Since  is only smooth, we could not really restrict the size of
is only smooth, we could not really restrict the size of 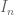 , but
, but  shrinking to zero would imply
shrinking to zero would imply  behaves badly near
behaves badly near 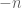 (or positive
(or positive  ) for large enough
) for large enough  . Since there is nothing particular about
. Since there is nothing particular about  being an integer, this showed
being an integer, this showed  should be “almost” non-analytic almost everywhere on large enough values in
should be “almost” non-analytic almost everywhere on large enough values in 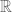 . However, if
. However, if  is analytic somewhere a translation argument showed this cannot exist. So
is analytic somewhere a translation argument showed this cannot exist. So  must be nowhere analytic and its translations also gradually “become worse”. But I am not sure if this is useful for anything.
must be nowhere analytic and its translations also gradually “become worse”. But I am not sure if this is useful for anything.
4 May, 2021 at 8:58 pm
julien PUYDT
The indicator function for the rational numbers, denote it by , has the property that for each
, has the property that for each  rational,
rational,  is zero hence analytic, even though
is zero hence analytic, even though  isn’t even continuous.
isn’t even continuous.
Granted, that doesn’t solve the question for all real, but it’s still a nice example, as it’s pretty trivial to explain to a young student and already shows how tricky things can become.
real, but it’s still a nice example, as it’s pretty trivial to explain to a young student and already shows how tricky things can become.
5 May, 2021 at 12:08 am
Anonymous
I actually thought of this same example, but didn’t end up writing it because I’m an amateur. Glad to see it actually got some attention :)
I was also wondering about solutions to slight variations of the problem. For example, what if we remove the smoothness condition on , or what if we want that
, or what if we want that  takes values in some set different than
takes values in some set different than  ? I was thinking something along the lines of
? I was thinking something along the lines of  taking values in some set
taking values in some set  , and then taking
, and then taking  to be the indicator function of a set
to be the indicator function of a set  that is invariant by translations under elements of
that is invariant by translations under elements of  . The case of the above comment would then be
. The case of the above comment would then be 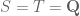 .
.
Yet another interesting variation would be replacing the difference by some other function of and
and 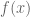 , for example there some or any arbitrary linear combination. I might be completely wrong, but something tells me that if we find an example for one linear combination, then we can easily modify it to an example for most (all?) linear combinations.
, for example there some or any arbitrary linear combination. I might be completely wrong, but something tells me that if we find an example for one linear combination, then we can easily modify it to an example for most (all?) linear combinations.
5 May, 2021 at 12:54 pm
Anonymous
This idea is applicable to any additive group of real numbers (which may be generated from any set
of real numbers (which may be generated from any set  of real numbers – as the smallest additive group containing
of real numbers – as the smallest additive group containing  ).
). is Hamel basis, then the smallest additive group containing
is Hamel basis, then the smallest additive group containing  is
is  .
.
It is interesting to observe that if
7 May, 2021 at 11:32 am
Aditya Guha Roy
If you demand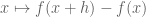 to be analytic for every
to be analytic for every 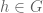 where
where  is an additive subgroup of
is an additive subgroup of 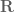 but
but  then taking
then taking  to be the indicator function of
to be the indicator function of  suffices, since in this case
suffices, since in this case  is clearly not analytic, and also
is clearly not analytic, and also 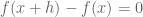 for every
for every 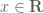 and every
and every 
5 May, 2021 at 2:16 am
Rafal Filipow
The question considered in the post is connected with the so called “the difference property in the sense of de Bruijn” (see [1], and a very good survey [2]).
We say that a family F of functions has the difference property if for each function f such that f(x+h)-f(x) belongs to F for each h, there are g in F and an additive function A such that f = g + A.
In [1], de Bruijn proved that the family of all analytic functions has the difference property. Consequently, if all differences f(x+h)-f(x) are analytic, there is an analytic g and an additive A with f=g+A. Now, if we assume that f is smooth, then both f and g are bounded on the unit interval [0,1]. It means that the additive function A is bounded on [0,1] as well, so A is in fact linear. All in all, f is analytic as a sum of 2 analytic functions.
Best,
Rafal Filipow
[1] N. G. de Bruijn, Functions whose differences belong to a given class. Nieuw Arch. Wiskunde (2) 23, (1951). 194–218.
[2] M. Laczkovich, The difference property. Paul Erdős and his mathematics, I (Budapest, 1999), 363–410, Bolyai Soc. Math. Stud., 11, János Bolyai Math. Soc., Budapest, 2002.
5 May, 2021 at 5:35 am
itaibn
First of all, it would be nice to have a short name for the property in the question. Perhaps “difference-analytic”? I suggest that this term is not restricted to smooth functions, but perhaps to arbitrary functions whose differences is analytic, since we might want to prove partial results such as that if such a function is continuous then it is . On the other hand, Julien’s remark suggests that there might exist pretty wild non-continuous difference-analytic functions, so it might be worth excluding them.
. On the other hand, Julien’s remark suggests that there might exist pretty wild non-continuous difference-analytic functions, so it might be worth excluding them.
I was hoping it might be possible to start with one difference-analytic function , and transform it into another difference-analytic function which is periodic. One approach I considered is by multiplying with an analytic function
, and transform it into another difference-analytic function which is periodic. One approach I considered is by multiplying with an analytic function  . Alas, this does not work:
. Alas, this does not work:
The first term is analytic, but we couldn’t possibly know that the second term is analytic without already knowing that is analytic.
is analytic.
On the other hand, the convolution of with a function
with a function  of compact support is difference-analytic, as
of compact support is difference-analytic, as
which is analytic since it is a convolution of an analytic function and a function of compact support, and such a convolution is analytic because a function is analytic iff it has a holomorphic extension. and
and  need to be regular enough so that the convolution makes sense.
need to be regular enough so that the convolution makes sense.
5 May, 2021 at 7:33 am
Terence Tao
It occurs to me that the Steinhaus lemma could be useful. For any![h \in [0,1]](https://s0.wp.com/latex.php?latex=h+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) , the function
, the function  is analytic, and so obeys bounds
is analytic, and so obeys bounds 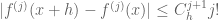 for all
for all  , all
, all ![x \in [-10,10]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B-10%2C10%5D&bg=ffffff&fg=545454&s=0&c=20201002) (say), and some constant
(say), and some constant  depending on
depending on  . As I mentioned in the main post, there is no uniformity assumed on the analyticity and so
. As I mentioned in the main post, there is no uniformity assumed on the analyticity and so 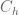 could behave in a bad way with respect to
could behave in a bad way with respect to  . However, if for each
. However, if for each  we let
we let  be the set of
be the set of ![h \in [0,1]](https://s0.wp.com/latex.php?latex=h+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) such that
such that  , then the
, then the  are measurable and exhaust
are measurable and exhaust ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) , hence one of the
, hence one of the  must have positive measure. The Steinhaus lemma then gives us an interval
must have positive measure. The Steinhaus lemma then gives us an interval 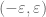 around the origin that lies in
around the origin that lies in 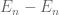 . Thus if
. Thus if  then there exists
then there exists  such that
such that 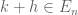 , hence for any
, hence for any ![x \in [-5,5]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B-5%2C5%5D&bg=ffffff&fg=545454&s=0&c=20201002) and any
and any  we have
we have
and hence by the triangle inequality we now have a uniform bound

whenever ,
,  , and
, and ![x \in [-5,5]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B-5%2C5%5D&bg=ffffff&fg=545454&s=0&c=20201002) . Not sure where to go from here (still not enough uniformity to pass to the limit in the Newton quotient) but it does seem one step closer to making
. Not sure where to go from here (still not enough uniformity to pass to the limit in the Newton quotient) but it does seem one step closer to making  analytic.
analytic.
5 May, 2021 at 8:28 am
Terence Tao
I took a look at de Bruijn’s paper mentioned in Rafal’s answer and it turns out he basically uses the same argument as above (but with Baire category instead of Steinhaus) and completes the argument as follows. For any![x \in [-1,1]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B-1%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) , the
, the 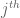 divided difference
divided difference  is of the form
is of the form 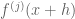 for some
for some  , where
, where  . On the other hand, since
. On the other hand, since  is bounded on say
is bounded on say ![[-2,2]](https://s0.wp.com/latex.php?latex=%5B-2%2C2%5D&bg=ffffff&fg=545454&s=0&c=20201002) , this divided difference is bounded by
, this divided difference is bounded by 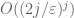 . From the previous bound and the triangle inequality we now have
. From the previous bound and the triangle inequality we now have
for any and
and ![x \in [-1,1]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B-1%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) , and this gives the analyticity of
, and this gives the analyticity of  in this interval, and similarly for the rest of the real line.
in this interval, and similarly for the rest of the real line.
Alternatively, one can integrate the inequality

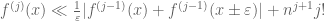
 , and iterate to obtain a similar estimate.
, and iterate to obtain a similar estimate.
using the fundamental theorem of calculus to conclude that
for either choice of sign
7 May, 2021 at 8:01 pm
duck_master
I think this basically means that you answered (this high-schooler’s) question. One note: Since we assumed a-priori that $f$ can be essentially an arbitrary function, the notation $f^{(j)}$ doesn’t really make sense unless it’s referring to some kind of divided difference (because $f$ can be arbitrary far from being non-differentiable as many times as you want). I think this invalidates the proof on a surface level but there’s a slightly modified version of it that doesn’t suffer from this problem.
By the way, I’ve never understood how we can get bounds of the type $|f^j|\leq CD^j j!$ for some $C, D$ for an arbitrary true real-analytic function $f$. I understand that any sequence of numbers $(a_j)_{j = 1}^{\infty}$ with bounds $|a_j|\leq CD^j j!$ is trivially the derivative sequence of a real-analytic function near zero by Taylor’s theorem, but I haven’t been able to come up with a converse of this (which would be that the derivative sequence of a real-analytic function can *only* be such a sequence).
7 May, 2021 at 8:08 pm
duck_master
Sorry, I don’t know how to write math-that-displays-properly on this comments section, so that’s why there are lots of dollar signs. I think it’s a math tag or something, but I don’t know. You should make it clearer somewhere.
Tests: \frac{1}{2}, \(\frac{1}{2}\), \[\frac{1}{2}\], \begin{equation}\frac{1}{2}\end{equation}, $$\frac{1}{2}$$
Again but with spaces for posterity: \ f r a c { 1 } { 2 } , \ ( \ f r a c { 1 } { 2 } \ ) , \ [ \ f r a c { 1 } { 2 } \ ] , \ b e g i n { e q u a t i o n } \ f r a c { 1 } { 2 } \ e n d { e q u a t i o n } , $ $ \ f r a c { 1 } { 2 } $ $
[Instructions for using LaTeX are at the bottom left of the blog – T.]
5 May, 2021 at 8:21 am
Márton Elekes
A function class C has the so called difference property, if the following holds: if f(x+h)-f(x) is in C for every h then f = g + A, where g is in C and A is an additive function (i.e. A(x + y) = A(x) + A(y) for every x,y).
In the following paper it was shown that the class of real analytic functions has the difference property:
de Bruijn, N. G.
Functions whose differences belong to a given class.
Nieuw Arch. Wiskunde (2) 23, (1951). 194–218.
This implies that if f is, say, measurable, and the differences f(x+h)-f(x) are all real analytic, then f itself is real analytic.
For more information on the difference property see e.g.
Laczkovich, M. (H-EOTVO-AN)
The difference property. Paul Erdős and his mathematics, I (Budapest, 1999), 363–410,
Bolyai Soc. Math. Stud., 11, János Bolyai Math. Soc., Budapest, 2002.
5 May, 2021 at 10:25 am
Hello
if we replace f differentiable or continuous instead of smooth what is the answer?
7 May, 2021 at 12:22 pm
Aditya Guha Roy
See section 1.6 from the measure theory textbook by prof. Tao.
5 May, 2021 at 10:37 am
Johan Aspegren
The sums and negations of analytic functions are analytic. From $A- B = A + (-B)$ you can just calculate $f(x+h) – f(x) – (f(x +h) – f(x)) = -2f(x)$ is analytic, thus f(x) is analytic?
5 May, 2021 at 11:29 am
Johan Aspegren
Sorry, a calculation mistake. $f(x+h) – f(x) – (f(x +h) – f(x)) = 0. $ I don’t know much about analytic functions, but I remember that if it holds on a point it holds in some interval. So $f(0+y) – f(0) +f(0) – f(0-y)= 2f(y) $ is analytic if $f$ is odd. $f(0+y) – f(0) +f(0) – f(0-y)= 0$ is if $f$ is even. Every analytic function is a sum of it’s odd and even parts so $f$ should be analytic because this holds for any $y$.
7 May, 2021 at 9:37 am
Johan Aspegren
It seems that for even part I need this $f(0+y) – f(0) – f(0) + f(0-y)= -2f(0) +2f(y)$. However, W.L.O.G we can assume that $f(0) = 0.$ Thus, $f(0 + h) – f(0) = f(h)$ is analytic is enough.
11 June, 2022 at 1:14 am
Mr.Postman
We are not elitistic or anything…all I got was one thumb down. Tell that kid that If she wants to do deep works she is in wrong company.
7 May, 2021 at 7:44 am
Donald
Take a hypothetical such function f. It must clearly be nonanalytic in every open neighbourhood. let k(x)=exp(-1/x) (0 for x<=0). let p(x) be formed by taking the talor expansion of f(x)/k(x) at 1. let P(x)=k(x)p(x). This is an analytic function at every point except 0. So f(x)-P(x) is not analytic, and has all derivatives 0 at 1.
(with the taylor series at point 0 not being effected.) flip this round, swaping 0 and 1. You now have a function F(x) such that F(x) is not analytic, and F(x) has a taylor series of 0 at points 0 and 1.
If you make this cyclic, the analytic difference property should hold. Even at the endpoints, its analytic at both sides, and the taylor series at the sides is the same, so analytic. Thus we have constructed a periodic function with this property. Contradiction.
(Probably an error somewhere here, don't know where.)
7 May, 2021 at 11:03 am
Anonymous
8 May, 2021 at 4:59 am
Aditya Guha Roy
Reblogged this on Aditya Guha Roy's weblog.
3 June, 2021 at 1:05 pm
Anonymous
Definitely
18 June, 2021 at 8:27 pm
Aditya Guha Roy
Another problem of a similar flavour is the following question from the Miklos Schweitzer competition, 2019 :
If is a measurable function such that
is a measurable function such that 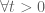 the function
the function 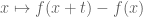 is locally integrable, then
is locally integrable, then  must also be locally integrable.
must also be locally integrable.
Unlike the original problem, this result can be proved in a rather elementary way by showing that if for some one has
one has 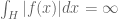 then one has either
then one has either 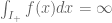 or
or  where $I_+ , I_-$ are respectively the set of points in
where $I_+ , I_-$ are respectively the set of points in 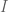 at which
at which  is
is  and eventually obtain that
and eventually obtain that  for some
for some 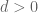 and some measurable
and some measurable  which would refute the local integrability of the difference function
which would refute the local integrability of the difference function 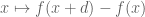 (for that particular choice of
(for that particular choice of 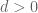 ).
).
20 June, 2021 at 10:35 am
Anonymous
Is there a smooth but nowhere real analytic function on ?
?
20 June, 2021 at 3:53 pm
Anonymous
https://en.wikipedia.org/wiki/Non-analytic_smooth_function#A_smooth_function_which_is_nowhere_real_analytic
21 June, 2021 at 11:00 am
Anonymous
It seem that in the example given in this wikipedia article, there is an error in the estimate for the radius of convergence because by Stirling’s formula
11 August, 2021 at 8:20 pm
Mehdi Morshedi
Could we use Fourier integral instead of Fourier series, and extend the same proof for non periodic case?
15 August, 2021 at 2:36 pm
h0sane
Question Dr. Tao: would the infamous piecewise function defined on R work? Where f := 0 for x <= 0 And e^{-1/x} otherwise? This is infinitely differentials but but the Taylor series converges to 0. Would this be an example of them your question holds? Thanks I’m advance, – fellow math student/learner/doer.
14 September, 2021 at 4:32 pm
More analysis questions from a high school student | What's new
[…] few months ago I posted a question about analytic functions that I received from a bright high school student, which turned out to be […]