Louis Esser, Burt Totaro, Chengxi Wang, and myself have just uploaded to the arXiv our preprint “Varieties of general type with many vanishing plurigenera, and optimal sine and sawtooth inequalities“. This is an interdisciplinary paper that arose because in order to optimize a certain algebraic geometry construction it became necessary to solve a purely analytic question which, while simple, did not seem to have been previously studied in the literature. We were able to solve the analytic question exactly and thus fully optimize the algebraic geometry construction, though the analytic question may have some independent interest.
Let us first discuss the algebraic geometry application. Given a smooth complex -dimensional projective variety
there is a standard line bundle
attached to it, known as the canonical line bundle;
-forms on the variety become sections of this bundle. The bundle may not actually admit global sections; that is to say, the dimension
of global sections may vanish. But as one raises the canonical line bundle
to higher and higher powers to form further line bundles
, the number of global sections tends to increase; in particular, the dimension
of global sections (known as the
plurigenus) always obeys an asymptotic of the form
It follows from a deep result obtained independently by Hacon–McKernan, Takayama and Tsuji that there is a uniform lower bound for the volume of all
-dimensional projective varieties of general type. However, the precise lower bound is not known, and the current paper is a contribution towards probing this bound by constructing varieties of particularly small volume in the high-dimensional limit
. Prior to this paper, the best such constructions of
-dimensional varieties basically had exponentially small volume, with a construction of volume at most
given by Ballico–Pignatelli–Tasin, and an improved construction with a volume bound of
given by Totaro and Wang. In this paper, we obtain a variant construction with the somewhat smaller volume bound of
; the method also gives comparable bounds for some other related algebraic geometry statistics, such as the largest
for which the pluricanonical map associated to the linear system
is not a birational embedding into projective space.
The space is constructed by taking a general hypersurface of a certain degree
in a weighted projective space
and resolving the singularities. These varieties are relatively tractable to work with, as one can use standard algebraic geometry tools (such as the Reid–Tai inequality) to provide sufficient conditions to guarantee that the hypersurface has only canonical singularities and that the canonical bundle is a reflexive sheaf, which allows one to calculate the volume exactly in terms of the degree
and weights
. The problem then reduces to optimizing the resulting volume given the constraints needed for the above-mentioned sufficient conditions to hold. After working with a particular choice of weights (which consist of products of mostly consecutive primes, with each product occuring with suitable multiplicities
), the problem eventually boils down to trying to minimize the total multiplicity
, subject to certain congruence conditions and other bounds on the
. Using crude bounds on the
eventually leads to a construction with volume at most
, but by taking advantage of the ability to “dilate” the congruence conditions and optimizing over all dilations, we are able to improve the
constant to
.
Now it is time to turn to the analytic side of the paper by describing the optimization problem that we solve. We consider the sawtooth function , with
defined as the unique real number in
that is equal to
mod
. We consider a (Borel) probability measure
on the real line, and then compute the average value of this sawtooth function
If one considers the deterministic case in which is a Dirac mass supported at some real number
, then the Dirichlet approximation theorem tells us that there is
such that
is within
of an integer, so we have
Theorem 1 (Optimal bound for sawtooth inequality) Let.
In particular, we have
- (i) If
for some natural number
, then
.
- (ii) If
for some natural number
, then
.
as
.
We establish this bound through duality. Indeed, suppose we could find non-negative coefficients such that one had the pointwise bound
After solving the sawtooth problem, we became interested in the analogous question for the sine function, that is to say what is the best bound for the inequality
Theorem 2 For any, one has
In particular,
Interestingly, a closely related cotangent sum recently appeared in this MathOverflow post. Verifying the lower bound on boils down to choosing the right test measure
; it turns out that one should pick the probability measure supported the
with
odd, with probability proportional to
, and the lower bound verification eventually follows from a classical identity

14 comments
Comments feed for this article
26 July, 2021 at 11:22 am
Anonymous
Is it possible to generalize the above optimal sawtooth and sine inequalities to similar inequalities for a general class of periodic functions?
27 July, 2021 at 11:04 am
Terence Tao
I think there should be analogous results for any periodic function that vanishes near the origin, though perhaps not with as precise a bound as we found for the sawtooth and sine functions. Perhaps one reasonable conjecture is that the optimal bound for, say, a trigonometric polynomial vanishing at the origin, is always comparable to .
.
16 September, 2021 at 1:50 pm
duck_master
I’ve devoted quite a bit of thought to this conjecture. Here’s what I have so far. For notational consistency I’ll refer to the trigonometric polynomial* which we’re studying as as you’ve done (when trying to estimate
as you’ve done (when trying to estimate 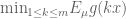 ). WARNING: this is an unusually long comment.
). WARNING: this is an unusually long comment.
First of all, one should restrict to be odd, or at the very least to be a function of expectation zero over its entire period. If
to be odd, or at the very least to be a function of expectation zero over its entire period. If  has a positive expectation, the uniform measure
has a positive expectation, the uniform measure  over the entire period already scores at
over the entire period already scores at  with respect to what we’re trying to optimize, which is within a constant factor of the trivial upper bound
with respect to what we’re trying to optimize, which is within a constant factor of the trivial upper bound 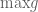 .* I expect similar things to hold for other functions that are periodic but not odd.
.* I expect similar things to hold for other functions that are periodic but not odd.
However, if we restrict to be odd (so that we can write
to be odd (so that we can write  ), then the two halves of this conjecture – upper and lower bounds – still vastly differ in difficulty. Upper bounds are easy: we know that
), then the two halves of this conjecture – upper and lower bounds – still vastly differ in difficulty. Upper bounds are easy: we know that 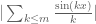 is always bounded (I believe strictly by 2 from graphing, though I lack a reference or proof for this at hand), so by the triangle inequality we can trivially conclude that
is always bounded (I believe strictly by 2 from graphing, though I lack a reference or proof for this at hand), so by the triangle inequality we can trivially conclude that  , so that
, so that 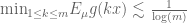 .
.
In contrast with upper bounds, lower bounds for odd are far more difficult, though I’ve managed (I think) to obtain the desired lower bound when
are far more difficult, though I’ve managed (I think) to obtain the desired lower bound when  . As in each case I considered, we just use the measure
. As in each case I considered, we just use the measure 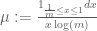 .*** **** To illustrate the difficulties I encountered in the
.*** **** To illustrate the difficulties I encountered in the  case, it suffices to consider the case
case, it suffices to consider the case 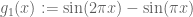 ; we can compute
; we can compute 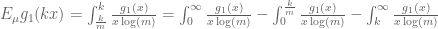 . Ordinarily, the first term would be the main term and be about
. Ordinarily, the first term would be the main term and be about 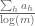 , whereas the other terms would be like error terms; however, in this case, the main term *cancels*! The second term is about
, whereas the other terms would be like error terms; however, in this case, the main term *cancels*! The second term is about  since
since  , and the third term is about some factor of
, and the third term is about some factor of  (I believe that
(I believe that 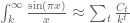 for appropriate constants
for appropriate constants  and integers
and integers 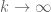 , though I again lack a reference or proof for this). Optimizing with respect to k using standard AM-GM trickery, we obtain a lower bound of
, though I again lack a reference or proof for this). Optimizing with respect to k using standard AM-GM trickery, we obtain a lower bound of  , which is still respectable, but far below what we want. (A generalization of this argument would give
, which is still respectable, but far below what we want. (A generalization of this argument would give  , where A is a positive rational number.)
, where A is a positive rational number.)
*Though I expect this to hold for functions that are much less regular, such as all analytic functions, or perhaps even all functions for which each successive derivative is only undefined at a set of measure zero.
**I actually discovered this while pondering the model case of the “even sawtooth” , which we can define as the only function of period 1 satisfying
, which we can define as the only function of period 1 satisfying 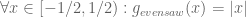 . Naturally, if we are allowed to study arbitrary functions
. Naturally, if we are allowed to study arbitrary functions  , then a natural approach is to find nice pointwise bounds
, then a natural approach is to find nice pointwise bounds 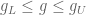 and to then estimate
and to then estimate  . The oddness constraint obviously makes this approach unavailable.
. The oddness constraint obviously makes this approach unavailable.
***Inspiration for this choice: I noticed that each of the optimal measures you constructed devoted roughly equal weight to the scales where $r:=\lceil\log_2(m)\rceil$, so I decided to choose a smooth measure that also shared this feature. Also, if
where $r:=\lceil\log_2(m)\rceil$, so I decided to choose a smooth measure that also shared this feature. Also, if  is negative, or the analogue of that, then simply flip this measure to the opposite side of zero.
is negative, or the analogue of that, then simply flip this measure to the opposite side of zero.
****I have a heuristic argument for this: Dyadically divide your measure into the scales measured at the previous footnote. The contribution to
into the scales measured at the previous footnote. The contribution to 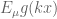 from scales that are much smaller than
from scales that are much smaller than 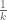 is close to zero because
is close to zero because  if
if  belongs to such a scale. The contribution from scales much *larger* than
belongs to such a scale. The contribution from scales much *larger* than 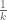 is also close to zero because multiplication by
is also close to zero because multiplication by  causes the distribution at this scale modulo period to resemble the uniform distribution (in the sense, at least, of distributions converging in probability), so its contribution will be about the expectation of
causes the distribution at this scale modulo period to resemble the uniform distribution (in the sense, at least, of distributions converging in probability), so its contribution will be about the expectation of  , which is also zero. Hence the only significant contributions will come from the scales close to that of
, which is also zero. Hence the only significant contributions will come from the scales close to that of 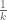 , which will have to be about a constant times the measure of such a scale. Since
, which will have to be about a constant times the measure of such a scale. Since  has
has  scales to accommodate, the mimimum expectation must be at most
scales to accommodate, the mimimum expectation must be at most 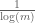 .
.
26 July, 2021 at 5:03 pm
Allen Knutson
You once told me it’d be a cold day in Hell when you wrote an algebraic geometry paper, with snow expected, so maybe I shouldn’t press you on the following issues (but I will!). If you want to talk about the “canonical line bundle”, you should probably ask that your variety be smooth. (Technically, it’s enough that your variety be Gorenstein.) Later (in “The space X” paragraph) it seems that you don’t actually want to require X smooth, and indeed don’t actually want the canonical sheaf to be a line bundle, just a reflexive sheaf. But you mention resolving the singularities, so maybe your varieties actually _are_ smooth?
27 July, 2021 at 11:02 am
Terence Tao
Fair enough, I’ve now added the hypothesis that the variety is smooth, though my understanding is that if the variety has only canonical singularities (and the canonical sheaf is reflexive) then any smooth resolution of the variety will produce the same volume. So one can just as well work with smooth models in this case.
15 August, 2021 at 2:27 pm
h0sane
Sorry I’m still a beginner, but by variety do you mean algebraic varieties ? Sorry if silly question I’m barely applying for PhDs this year so forgive me for my naive ness. I briefly studied them in my intro to Riemann surface course via Algebraic Curves & Riemann surfaces by Miranda. Thank you – fellow math student.
26 July, 2021 at 6:35 pm
Anonymous
Minor typos: The last equation is missing an equals sign and the last paragraph is trying to put the accent over the j and not the second e in Fej\’er
[Corrected, thanks – T.]
27 July, 2021 at 6:56 pm
Rex
What do you mean by in the phrase “for which
in the phrase “for which  does not admit a birational embedding into projective space”. The divisor?
does not admit a birational embedding into projective space”. The divisor?
[Yeah, or more precisely a complete linear system of divisors. I guess this is more commonly denoted , will edit to reflect this. -T]
, will edit to reflect this. -T]
28 July, 2021 at 9:59 pm
Rex
Let me spell this out just to make sure I understand correctly. We are saying there is no birational embedding of into a projective space such that the pullback of (the linear system of)
into a projective space such that the pullback of (the linear system of)  gives the linear system
gives the linear system  ?
?
31 July, 2021 at 10:41 am
Terence Tao
I’m not sure that’s an equivalent formulation. The way it is normally phrased is that each natural number induces a morphism (called the
induces a morphism (called the 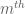 pluricanonical map) from
pluricanonical map) from  to the projective space
to the projective space 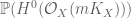 formed by evaluating the linear system
formed by evaluating the linear system  at every point and projectivising. The property of being of general type is precisely equivalent to this canonical map being a birational embedding for large enough
at every point and projectivising. The property of being of general type is precisely equivalent to this canonical map being a birational embedding for large enough  . The result of Hacon-McKernan, Takayama, and Tsuji referred to in the blog post asserts that the bound for “large enough” can be made uniform in the dimension
. The result of Hacon-McKernan, Takayama, and Tsuji referred to in the blog post asserts that the bound for “large enough” can be made uniform in the dimension  of
of  (this is related to the “minimal model program” in algebraic geometry, though I am not familiar with the details). The examples we have show that the bound still needs to grow quite quickly in
(this is related to the “minimal model program” in algebraic geometry, though I am not familiar with the details). The examples we have show that the bound still needs to grow quite quickly in  (at least
(at least  , to be precise). But as far as I know, this does not rule out the possibility of having a non-pluricanonical birational embedding into a lower dimensional projective space. I’ve modified the text in the blog post to try to clarify this point.
, to be precise). But as far as I know, this does not rule out the possibility of having a non-pluricanonical birational embedding into a lower dimensional projective space. I’ve modified the text in the blog post to try to clarify this point.
6 August, 2021 at 1:40 pm
BabaEpsilon
Hi Terence Tao the Great,
The legend says that every field of mathematics you get into, you advance the field.
I would like you to get into Geometric complexity theory because it is the most promising approach towards solving P vs NP we have right now.
6 August, 2021 at 10:51 pm
Anonymous
Don’t worry verry much,
You wait a little time , Pro Tao certainly makes maths community going from this amazing to another amazing. ProTao is still very young, but he has published more 300 papers within short time, this has not been made by any other mathematician in the world if considering the same his generation. By the way, he is still a human , he is not a machine, he needs much time to rest, he spends a little time in caring his family . But , I really inform you that pro Tao has made a great breakthrough on Navier Stokes existence and smoothness this year. Only owner of this Clay miillenium award is pro Tao. I am allowed to reveal my name, but I am always near pro Tao every minute, every hour.
Bye,
7 August, 2021 at 9:22 pm
twocents
If you noticed he does not get into speculative stuff (which includes geometric complexity theory) but observes ‘expert’ opinion which he gets a lot and there are a lot of self-proclaimed experts out there and he only goes in after a convincing argument. He is not Gauss but we know he is more talented than anyone anyone has known.
15 August, 2021 at 2:26 pm
🔜 i’ll get it: Varieties of general type with many vanishing plurigenera, and optimal sine and sawtooth inequalities. #TerenceTheGoat – Mathematics, for all Mankind!
[…] Varieties of general type with many vanishing plurigenera, and optimal sine and sawtooth inequalitie… […]