Asgar Jamneshan and myself have just uploaded to the arXiv our preprint “The inverse theorem for the Gowers uniformity norm on arbitrary finite abelian groups: Fourier-analytic and ergodic approaches“. This paper, which is a companion to another recent paper of ourselves and Or Shalom, studies the inverse theory for the third Gowers uniformity norm
Theorem 1 (Inverse theorem for) Let
be a finite abelian group, and let
be a
-bounded function with
for some
. Then:
- (i) (Correlation with locally quadratic phase) There exists a regular Bohr set
with
and
, a locally quadratic function
, and a function
such that
- (ii) (Correlation with nilsequence) There exists an explicit degree two filtered nilmanifold
of dimension
, a polynomial map
, and a Lipschitz function
of constant
such that
Such a theorem was proven by Ben Green and myself in the case when was odd, and by Samorodnitsky in the
-torsion case
. In all cases one uses the “higher order Fourier analysis” techniques introduced by Gowers. After some now-standard manipulations (using for instance what is now known as the Balog-Szemerédi-Gowers lemma), one arrives (for arbitrary
) at an estimate that is roughly of the form
So the key step is to obtain a representation of the form (1), possibly after shrinking the Bohr set a little if needed. This has been done in the literature in two ways:
- When
is odd, one has the ability to divide by
, and on the set
one can establish (1) with
. (This is similar to how in single variable calculus the function
is a function whose second derivative is equal to
.)
- When
, then after a change of basis one can take the Bohr set
to be
for some
, and the bilinear form can be written in coordinates as
for somewith
. The diagonal terms
cause a problem, but by subtracting off the rank one form
one can write
on the orthogonal complement offor some coefficients
which now vanish on the diagonal:
. One can now obtain (1) on this complement by taking
In our paper we can now treat the case of arbitrary finite abelian groups , by means of the following two new ingredients:
- (i) Using some geometry of numbers, we can lift the group
to a larger (possibly infinite, but still finitely generated) abelian group
with a projection map
, and find a globally bilinear map
on the latter group, such that one has a representation
of the locally bilinear formby the globally bilinear form
when
are close enough to the origin.
- (ii) Using an explicit construction, one can show that every globally bilinear map
has a representation of the form (1) for some globally quadratic function
.
To illustrate (i), consider the Bohr set in
(where
denotes the distance to the nearest integer), and consider a locally bilinear form
of the form
for some real number
and all integers
(which we identify with elements of
. For generic
, this form cannot be extended to a globally bilinear form on
; however if one lifts
to the finitely generated abelian group
To illustrate (ii), the key case turns out to be when is a cyclic group
, in which case
will take the form
This concludes the Fourier-analytic proof of Theorem 1. In this paper we also give an ergodic theory proof of (a qualitative version of) Theorem 1(ii), using a correspondence principle argument adapted from this previous paper of Ziegler, and myself. Basically, the idea is to randomly generate a dynamical system on the group , by selecting an infinite number of random shifts
, which induces an action of the infinitely generated free abelian group
on
by the formula
This transference principle approach seems to work well for the higher step cases (for instance, the stability of polynomials result is known in arbitrary degree); the main difficulty is to establish a suitable higher step inverse theorem in the ergodic theory setting, which we hope to do in future research.

15 comments
Comments feed for this article
28 December, 2021 at 1:57 pm
Anonymous
Is it possible to unify/combine the analytic and ergodic approaches?
29 December, 2021 at 10:30 am
Terence Tao
I believe this will eventually be the case. Certainly there are close analogies between the two approaches and a partial dictionary between the two; to give just one example, being measurable with respect to the Kronecker factor in the ergodic theory approach corresponds to being well approximated by a linear combination of a bounded number of Fourier characters in the Fourier-analytic approach. The framework of nilspace structures on hyperfinite abelian groups is in some sense a partial unification of the two approaches, though at our current level of understanding, nilspaces don’t seem to fully capture all the dynamical structure that the ergodic theory approach exploits (or all of the additive combinatorial structure that the Fourier analytic approach exploits). Hopefully as research advances, these approaches will become more unified, but it is still a work in progress.
29 December, 2021 at 1:00 am
Helen
I have passed the entrance exam,and making effort to become a good student in math,and trying to understand your blog~
31 December, 2021 at 9:10 pm
Rohan Bhardwaj
Dear Tao,
Since you have solved a part of Collatz Conjecture, I hope you may help me.
Will it be helpful to find a series of odd numbers that follow Collatz conjecture?
Thank you
Best
Rohan
4 January, 2022 at 5:45 pm
Michael Hunter
Is your work primarily in creating binding geometric structures for prime distributions, to upper and lower bound for a measure of convergence/predictability?
I’m enjoying reading your posts!
Have an awesome day.
13 January, 2022 at 2:52 pm
CFNB
Line 7 of the post: “…on an arbitrary finite abelian group $f$”, should replace f by G.
Additionally, in the abstract for the paper, the first line reads “…for the Gowers uniformity norm […] on an arbitrary finite group G”. Surely this should be an arbitrary finite *abelian* group G?
[Corrected, thanks – T.]
20 February, 2022 at 7:54 am
Jas, the Physicist
How do I even begin to understand this blog. Should I just start with your real analysis lecture series/notes/book?
21 February, 2022 at 5:54 am
Uwe Stroinski
Definition 1.4 (ii) of regular Bohr sets in your paper is not consistent with your usual definition.
[I don’t see the inconsistency; the definition is taken from Definition 4.24 of my book with Van Vu. -T]
3 March, 2022 at 8:46 am
Uwe Stroinski
In that case it is a minor typo. One needs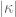 in the inequality.
in the inequality.
[Thanks, this will be corrected in the next version of the ms – T.]
27 May, 2022 at 2:14 pm
Notes on inverse theorem entropy | What's new
[…] the norm on an arbitrary finite abelian group, the recent inverse theorem of Jamneshan and myself gives (after some calculations) a bound of the polynomial form on the -entropy for some , which […]
15 August, 2022 at 3:16 pm
Anonymous
Is there a good reference for Calderon Transference principle?
16 August, 2022 at 11:06 am
Anonymous
A paper titled “Ergodic theory and translation invariant operators” is a good place to start.
16 August, 2022 at 11:35 pm
Dilip Kulkarni
3x-1 seems to reach. Is this something well known and has attention like 3x+1
x=1 -> 3.1-1=2, 2/2 =1 loop 1-2-1
x=2 –> 1 loop
x=3 –> 8–>4–>2–>1 loop 1-2-1
x=4 –> 2–>1 loop
x=5 –> 14 –>7–>20–>10 –>5 loop to 14
x=6 –> 3 –>8–>4–>2–>1 loop to 2
x=7 –> 20 –>10–>5–>14–>7–>20 loop to 7
x=8 –> 4–>2–>1
x=9 –>26–>13–>38–>19–>56–>28–>14–>7–>20 loop to 7
x=10 –>5–>14 –>7–>20–>10 loop
10 March, 2023 at 8:59 am
A Host–Kra ${bf F}^omega_2$-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the $U^6({bf F}^n_2)$ norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse th
[…] developed in that paper (see also this paper of Towsner for a closely related principle, and this paper of Jamneshan and I for a refinement). In a paper with Bergelson and Ziegler, we were able to establish Conjecture 2 in […]
10 March, 2023 at 9:00 am
A Host–Kra ${bf F}^omega_2$-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the $U^6({bf F}^n_2)$ norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse th
[…] developed in that paper (see also this paper of Towsner for a closely related principle, and this paper of Jamneshan and I for a refinement). In a paper with Bergelson and Ziegler, we were able to establish Conjecture 2 in […]