Last updated: Feb 24, 2024
Solving Mathematical Problems (Second edition)
Terence Tao
Oxford University Press, Oxford, England: 2006
Paper, 128 pages. ISBN13: 9780199205608
ISBN10: 0199205604
This book discusses various Olympiad level problems and how one can go about trying to solve them. It is the second edition of an earlier first-edition run. It has also been translated into Portugese as “Como resolver problemas matemáticos” by Paulo Ventura Araújo for the Sociedade Portuguesa de Matemática; into Chinese as “解题·成长· 快乐——陶哲轩教你学数学” (ISBN 9787301154472) by Qinglin Yu (于青林) for Peking University Press; and into Italian as “Risolvere problemi matematici. Il mio punto di vista” (ISBN 8896973880) by Samuele Maschio amd Carlo Càssola for Scienza Express Edizioni SNC (reviewed here by Alberto Saracco).
It has been reviewed for the Notices of the American Mathematical Society by Loren Larson.
- Sample chapters (Preface, strategy, problems in number theory)
— Errata —
- In page 2, “Problem 1.1 question” should just be “Problem 1.1”.
- In page 6, second to last paragraph, “once can avoid” should be “one can avoid”.
- In page 7, “ompute” should be “compute”, and “put clear denominators” should be “clear denominators”. On the fourth displayed equation,
should be
, and
should be
.
- In page 9, example (e), “876” should be “376”. “which are exactly” should be “which have exactly”. In example (d),
should be
.
- In page 16, bottom, “217” should be “
“. “if this question is true, then the original question is true” should be “if the answer to the original question is “yes”, then so is the answer to this question”.
- In page 25, third paragraph: one of the “n”s should be in math mode.
- In page 33, Exercise 2.5: For an additional challenge, prove this exercise without using Bertrand’s postulate.
- In page 35: In the quote, “that was originally” should be “than was originally”.
- In page 37, second display:
should be
.
- In page 40, “smells heavily on” should be “smells heavily of”.
- In page 42,
should be
in one of the displays.
- In page 44, 5ab should be (13) (two occurrences)
- In page 45, Problem 3.4, there should be no commas between
and
. “are all integers” should be “are all distinct integers”. One should delete all references to
, for instance deleting the factor
in the problem box, and also
and
in the next page.
- In page 46, in the sentence “But polynomials only have as many degrees of freedom as their degree”, insert “with leading coefficient 1” after “polynomials”.
- In page 47, Exercise 3.7, the
should be a
, one should look at
rather than
, and “are integers” should be “are distinct integers”.
- On page 50, the intersection of BC and AI should be labeled D.
- In the second to last line on page 52, “either
or
” should be “either
or
“.
- In the diagram on page 53, the angle at D should be
, and the angle at E should be
.
- In page 58, one of the instances of
should be in math mode (like all the other instances). “on the same side of
” should be “on the same side of
“.
- In page 63, third line, “inner square” should be “inner rectangle”.
- In page 65-66, the informal geometric argument given is incomplete, the issue being that just because the sum of side lengths of
is (say) bigger than 1, it is not immediately obvious that the same is true for, say,
. But one can check using algebra that if
, then
, and similarly with the inequalities reversed; this allows the argument as stated to be made rigorous. (One can also argue by considering the rectangle with the narrowest side, and showing that it is adjacent to one which is even narrower if its sides do not add up to length 1.)
- In page 66, problem 44, there is a
missing at the end of the string of equations, thus
.
- Page 74, second paragraph: “this can be true is of” should be “this can be true is if”
- Page 76-77: The informal topological argument here does not quite work as stated, for if two rectangles with integer horizontal lengths (say) are connected by a common horizontal line segment rather than a common vertical one, then the lengths do not add together as suggested in the argument. To fix this, one needs a more complicated colouring scheme. Namely, one colours the interiors of rectangles with integer horizontal lengths green, and those with integer vertical lengths red. As for the edges, one colours the (open) vertical edges green and the (open) horizontal edges red. There are a few remaining corners which are not on any open edge that remain to be coloured; these can be assigned either red or green arbitrarily. With this colouring, any green path between the two horizontal edges of the big rectangle can be used to deduce the integer horizontal length of that rectangle, and similarly for a red path between the two vertical edges. (There are also several other proofs, for instance one can induct on the number of rectangles.)
- In page 77, second-to-last paragraph, “it seems that the assertion is plausible” should be “it seems plausible that the procedure always terminates”.
- In the diagrams on page 79 and page 82, the labels C and D should be switched.
- In page 82, “X is a quarter-length or less from M” should be “X is a quarter-length or more from M”.
- In page 87, second-to-last paragraph, “eliminated (c)” should be “eliminated is (c)”.
- In page 90, second paragraph: “ths game” should be “this game”.
- In page 92, third paragraph: “that it is a sure” should be “that is a sure”. In the second to last line, “all sure losers, as we have shown above” should be “all sure winners, as we have shown above”.
- In page 95: change all occurrences of “rouble” to “ruble” (for consistency). In the third paragraph, “in terms of equation” should be “in terms of equations”.
- In page 96, last line: “restricted to between” should be “restricted to lie between”.
- In page 97, second paragraph: “
” should be “
or
“, and so the example values of s should now read
.
- In the references, “G.A. Hardy” should be “G.H. Hardy”.
— Errata to the Chinese version —
- In p. 40(d), “如果k是正奇數,則 1^k+2^k+…+n^k 可被 n+1 整除”, n+1 should be n(n+1)/2.
- In p. 76, “幸好第一個因數(p-1)i 和 p^2 是互質的(因為(p-1)i 和 p 是互質的)”, the i’s should be factorial symbols.
- In p. 146, “與一些三角形和圓有關的∠APF,看起來似乎是比較「主流」的角”, APF should be ABF.
- In p. 154, “若 n 為偶數,令 m=(n+2)/1”, (n+2)/1 should be n/2+1.
- In p. 202, ” 我們只能說 s = ±4 (mod 20),因此羊的數量可能是 4、16、24、36、44、56 等”,
” should be “
or
“, and so the example values of s should now read
.
Thanks to Paulo Ventura Araújo, Thomas Drucker, Tathagata Gupta, Percival Li, ouzi, Cecil Rousseau, Naoki Sato, dsilvestre, Arnstein Skåra, Tom Verhoeff, Weiyu Xu, Li Yan, Au Cheuk Yin, and 현민 오 for corrections.

41 comments
Comments feed for this article
31 July, 2007 at 8:37 am
Anonymous
404 on the link to the first edition.
23 February, 2008 at 6:32 pm
dsilvestre
I think on page 52 on the last two lines where it says “because we want to prove that either B=60º or A=Y”, it should instead say “because we want to prove that either A=60º or B=Y”.
(I wrote A for alfa, B for beta, etc)
25 February, 2008 at 9:38 am
Terence Tao
Thanks for the correction!
8 April, 2008 at 2:32 am
Radu Grigore
Nitpick: In Chapter 2 Wilson’s theorem is stated as “(n-1)!+1 is a multiple of n if and only if n is a prime number” and the next page says that “we do not consider 1 to be a prime number.”
8 December, 2008 at 7:41 pm
percyli
I think that there is an “D” missing on page 50’s graph.
9 December, 2008 at 6:56 am
Terence Tao
Thanks!
15 December, 2008 at 3:12 pm
MathOMan
Concerning page 76-77. , the other using the tensor calculus. You can find it here.
, the other using the tensor calculus. You can find it here.
Your corrected solution is beautiful. I have discussed it in my blog alongside two other solutions, one using integration of
Above you also mention the possibility of “induction on the number of rectangles” — how does that work?
19 March, 2009 at 9:00 am
Antonio
Greetings,
In Portuguese Mathematics is Matemática, without the h.
The title of your book in Portuguese is “Como resolver problemas matemáticos”, by “Sociedade Portuguesa de Matemática”. [Corrected, thanks – T.]
16 March, 2010 at 10:58 am
Livro de Terence Tao Como Resolver Problemas Matemáticos « problemas | teoremas
[…] Solving mathematical problems: a personal perspective, Deakin University Press, 1992. No post Solving Mathematical Problems, de 1997, no seu blogue What’s New, sobre a 2.ª edição do original Solving Mathematical […]
17 May, 2010 at 3:07 pm
marco
es posible descargar sus textos en formato pfd?
gracias
19 May, 2010 at 1:43 am
palibacsi
I would appreciate it, if occasionally higher-level mathematical problems were discussed in a similar style and by various authors, where even the eventually dismissed ideas and avenues of attack are documented. I hope there is room for it at least on the internet.
I think it would be interesting to see how different mathematicians make use of the existing literature while working on a problem and how they find the sources that eventually turn out to be helpful.
If something like this already exists, I will be glad to know where.
My impression is that far too many students get the false impression that they will never be able to produce the kind of polished solutions and proofs they always read and I hope that this can be overcome in this way. The next step would be to draw the students’ attention to these discussions.
Perhaps the polymath projects are quite close to it, but on a level too high to reach a large enough part of the students.
19 May, 2010 at 1:50 am
palibacsi
On top it says that the second edition of Solving Mathematical Problems has 150 pages, but the one on my desk has only 103 pages. If there are another 47 pages of this wonderful book, I must get them!
19 May, 2010 at 7:26 am
Terence Tao
Hmm, strange, I don’t remember where that number came from. The official OUP page lists 128 pages (presumably counting blank pages, etc.), so I’ll go with that number.
19 May, 2010 at 12:05 pm
palibacsi
Counting blank pages, etc., there are actually 128 pages.
12 April, 2012 at 3:56 pm
jh
Hello, professor, i got a question for (d) of p.9 of this book, “If k is a positive odd number, then 1k +2k +. . .+nk is divisible by n+1.”
when
n=5 k=3,
1^3+2^3+3^3+4^3+5^3=225 (not divisible by 6)
in case,
i think you intended when n=(even) whole expression is divisible by n(n+1)/2
(you showed it at problem 2.6)
[Correction added, thanks – T.]
13 September, 2012 at 5:00 pm
João Jorge
Hi there, on problem 2.6, page 25, there is something that I can´t see. I suppose it’s obvious. “If the two factors are coprime, then our objective is equivalent to proving both of” “(factor 1)|(expression) and (factor 2)|(expression)”. Why it´s necessary the two factors being coprimes ? It’s maybe a dumb question but please someone enlighten me !
Thanx,
Regards.
14 September, 2012 at 8:08 am
Terence Tao
The claim “a|n and b|n” is not logically equivalent to “ab|n” in general, but instead to “lcm(a,b)|n”, where lcm(a,b) is the least common multiple of a and b. For example, to show that an integer n is divisible by 24=6*4, it is insufficient to demonstrate that n is divisible by 6 and 4 separately (n=12 is a counterexample). Of course, if a and b are coprime, then lcm(a,b)=ab, and so logical equivalence is restored in this case.
On the other hand, the converse implication is always true: “ab|n” implies both “a|n” and “b|n”, regardless of how many common factors a and b have.
14 September, 2012 at 12:12 pm
João Jorge
Hi again,
First thanx for the reply, and second for the elucidation.
It was kind of obvious, but I wasn´t seeing it.
By the way I am studying your book “analysis”. I’m a portuguese student on 2ºyear of 3 on economics, on a further 2 years masters degree.
My course don’t have much mathematics, so I’m teaching myself.
I do it because I like maths, and I need a strong basis to be more analitical, quantitative, beeing more capable of study advanced technical books, and improve mind thinking.
I have good grades on mathematics now, but not really good ones. I think I’m very clever, “small genius”, but always frooze on tests. Some teachers said that I have an excellent mathematical reasoning.
On 12º my math teacher gave me 1 more value on 0-20 scale because of a probablistic problem that I solved with sequencies.
Do you have any suggestion how I should aproach tests?
With a final comment I would like to express my admiration for your work, community interaction, and the reasons why you work on mathematics.
Thanx, and good luck for everything in your life,
Regards.
15 January, 2015 at 9:49 am
Soumyadip
Mr. Tao. You are doing a really great and selfless job. Much respect. :)
11 July, 2015 at 6:00 am
译:解决数学问题 by 陶哲轩 | 万里风云
[…] 解决问题,无论是对作业题还是对人类未曾解决的问题,当然都是数学学科的重要方面,尽管这并不是唯一的方面。在今后你的研究生涯里,你会发现,人们往往通过知识(包括你自己领域和别的领域的知识)、经验、耐心、和勤奋工作来解决问题;但是对于中小学、大学、或者数学竞赛里的题目,人们需要一套稍微与众不同的问题解决技巧。我写过一整本关于在这个层面上解决数学题的书;而且,那本书的第一章就在讨论通用的问题解决策略。当然,市面上也有很多其他关于解决问题的书,比如波利亚的《怎样解题》——我自己在准备数学奥林匹克竞赛时,就在学习这本书。 […]
18 July, 2016 at 8:29 am
Solving mathematical problems | nguyen Huynh Huy's Blog
[…] mathematics competitions one needs a slightly different set of problem solving skills. I do have a book on how to solve mathematical problems at this level; in particular, the first chapterdiscusses general problem-solving strategies. There […]
5 January, 2018 at 5:54 am
404
In page 92, second last line: “symmetry 4 x 3, 4 x 2, 4 x 1 are all sure losers, as we have shown above” should be “symmetry 4 x 3, 4 x 2, 4 x 1 are all sure winners, as we have shown above”.
[Correction added, thanks – T.]
19 May, 2018 at 8:44 am
gpanda
Hi Prof. Tao, on Problem 2.2 in Ch. 2 page 16, “(If 10 people each randomly pick one two-digit number, there is a sizeable (9.5%) chance of a match, …”. I’ve no idea how to get 9.5%, if you mean the probability of at least two people choose a same 2-digit number, shouldn’t it be 1 – P(90,10)/(90^10) = 40.5%? Like Birthday problem?
Thanks.
29 December, 2018 at 6:17 am
innosolo
I have been trying to study this book. Please how do I download it for study?
4 June, 2020 at 9:30 pm
Totsuka
Hi Mr. Terence. Your book is very exciting to me. I have a question. In page 48,Exercise 3.8. If the polynomial is 5x-3, f(a)-f(b) can not equal 1, but 5 or -5 when a and b are consecutive.I think not enough assumptions. Could you give me a reply?
6 June, 2020 at 7:45 pm
Terence Tao
This example is consistent with the exercise. (The exercise asks to prove that it is not possible for f(a)-f(b) to equal 1 unless a,b are consecutive integers.)
8 June, 2020 at 1:20 am
Totsuka
Thank you for your kind reply. I understood that I took a mistake with an English grammar. I wish you the best of luck!
10 June, 2020 at 12:19 am
Usman Nizami
Sir Tao,
Can these ideas are helpful for gaps in Prime numbers If we look at prime numbers they give us an interesting patterns. We divide prime numbers in three categories. Lower prime numbers (less than a finite integer M), Medium prime numbers (Greater than M but less than N ) and Higher prime numbers (greater than or equal to N{ a arbitrarily large integer greater than M}). Working with lower prime is like working in quantum mechanics with sub atomic particles and asking why 1 is not a prime and 2 is prime and so on . Working with higher prime is like talking about black holes and large scale structure of space time . While medium prime numbers are finite but can be made as many as we want. So let us work on them regarding some conjecture of number theory like Goldbatch’s conjecture , Riemann Hypothesis , twin prime like conjectures etc.
I have some suggestions.
1) Redefining Peano axioms
2) Using ZFC axioms for some theorems
3) Defining addition and division in terms of basic multiplication and subtraction instead doing opposite, which is very common now a days.
4) Using 0 and 5,6,7 and multiplication and subtraction, with subtraction the basic axioms like induction will be used instead additions are used now a days. (See Book on Analysis by Prof. Terence Tao. )
5) Defining 2 , 3 , 8, 9, 20 etc. in terms of 0, 5 or 7 the way distance is defined in terms of speed of light in Relativity .
7) Redefining Prime numbers to include non euclidean Prime numbers ,
{Taking fun of S Aaronson into axioms https://www.scottaaronson.com/blog/?p=1948}. Aaronson said “So then, do you think that statements of arithmetic, like there being no prime number between 24 and 28, might also be like the Parallel Postulate? That there might be some other, equally-valid “non-Euclidean arithmetic” where there is a prime between 24 and 28? What exactly would one mean by that?”
28 September, 2020 at 6:39 pm
현민 오
On page 58, “if B, D are on the same side of AB” I think AB should be AC
[Correction added, thanks – T.]
20 February, 2022 at 8:20 am
Jas, the Physicist
I will do my best.
18 March, 2022 at 4:27 am
Maths-student
A question regarding page 38, Problem 3.2:
Are we not done already after finding that f(2^n) = 2^n (now called (1))?
Because of (c) we know that if our input increases by 1, our output has to increase by at least 1 as well (for integers). (1) shows that increasing the input by 1 cant increase the output by more than 1, as counting onward to the next power of 2 would otherwise hurt either (1) or (c). Isnt that enough already to show f(n) = n for all positive integers n?
Greetings
[Yes, this works also. -T]
8 November, 2022 at 4:09 am
Les rectangles revisités une fois de plus - Math 'O Man
[…] une petite recherche sur internet, je me rends sur son blog personnel et j’y trouve une liste d’errata où il corrige, entre autres, cette preuve. Voici l’amélioration qu’il […]
3 October, 2023 at 3:53 am
Anonymous
Hallo, does anyone know where can i find the solutions for the exercises in this book?
22 October, 2023 at 7:38 am
Anonymous
I think in page 19, under 2.2 Diophantine equations, “even if everything is integral” should be “even if everything is integer” and after that, “integral factorization” should be “integer factorization”. Or is only me misunderstanding the words.
8 November, 2023 at 11:46 am
Anonymous
Hi everyone, in page 57 Theorem 4.2, the fact that PQT and PTR are similar triangles ist not so clear for me. In the book it says only: “observe that PQT is similar to PTR”. Can someone please give a proof of that to me.
9 November, 2023 at 3:17 pm
Terence Tao
10 November, 2023 at 12:32 pm
Anonymous
Thank you very much for the explanation. It’s now clear to me!
9 December, 2023 at 11:32 am
Anonymous
Hi Professor, I have a question on page 31-32. at the bottom of page 31 it says that “we can ‘double up’, making use of the fact that (-a)^2=a^2. It really confused me. I can’t see why we can get the expression 1/2[1/1^2+1/2^2+…+1/(p-1)^2] (mod p) from the fact that (-a)^2=a^2. Can you please explain how the cancelation or combination works here?
9 December, 2023 at 7:10 pm
Terence Tao
For instance, if , we are using
, we are using  to observe that the quantities
to observe that the quantities  and
and  are equal to each other, and hence equal to their average:
are equal to each other, and hence equal to their average:
But, modulo 5, is equal to
is equal to 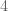 , and
, and  is equal to
is equal to  , so this expression can be rearranged as
, so this expression can be rearranged as
10 December, 2023 at 2:15 am
ljoyxa
I think you are talking about p=5. But I have got the idea. I would never figure it out by myself, if you haven’t answer that. I thought there were some combinations happening. Thanks a lot!
7 February, 2024 at 12:23 pm
ouzi
Hi Professor Tao, I am reading you book and I think I have found a typo in page 42 about the property homogeneous polynomials. It says there . I think the
. I think the  here should be
here should be  with n the degree of the homogeneous polynomial.
with n the degree of the homogeneous polynomial.
[Erratum added, thanks – T.]