Structure and Randomness: pages from year one of a mathematical blog
American Mathematical Society, 2008
298 pages
ISBN-10: 0-8218-4695-7
ISBN-13: 978-0-8218-4695-7
Last updated Nov 25, 2022
This is a book version of my blog, covering many (though not all) of my articles in 2007, reworked into a publishable format (and in particular, with formal and updated references).
A draft copy of the book is available here. Note that the formatting for this internet version is significantly different from that in the final print version, in particular the page numbering does not correspond at all.
Here is a (2MB) PDF file containing the front cover of the book.
The official AMS web page for this book is here.
A review of the book for the American Scientist is here.
Here is a review for the MAA.
— Errata —
- Page 21: In Proposition 1.8,
should be
.
- Page 22: In Proposition 1.10,
should be
.Page 51: In Lemma 1.34(2),
should be
.
- Page ???: In the start of Section 1.9, the requirement
should be added to the definition of a linear recurrence sequence.
- Page 54: The phrase “nonstandard ultrafilter on
” requires some clarification. It should be “ultrafilter on
that extends an ultraproduct of nonprincipal ultrafilters on
“.
- Section 2.2, page ???: “need thus need” should be “thus need”.
- Page ???: In the proof of Lemma 2.28, in the final two displays, the left absolute value and integral signs should be interchanged.
- Page 86: In the final display, the exponent of
on the LHS should be deleted. Similarly on the first display of page 87.
- Page 95, Figure 1: The graph of
is missing two edges (namely, the long diagonal edges between opposite corners of the graph).
- Page 96: The inequality
is only valid for connected graphs with at least one cycle. In general, one only has
. One must then delete all terms involving the number 6 in the rest of the section. One can then replace “To solve the optimisation problem exactly, one needs to solve a cubic; but we can perform a much cheaper computation” by “One can solve the optimisation problem exactly, but we can perform a cheaper computation”.
- Page 101: Footnote 67 is incorrect and should be deleted.
- Page 102:
should be
.
- Page 103: The sentence “More generally, any Riemannian manifold…” is incorrect and should be deleted, replaced instead with the sentence “Similarly, the hy0erbolic plane
is isomorphic to
“.
- Page 104: In first paragraph: the modular curve should be
. In the footnote, add “and an obvious left action of
,” after the final comma.
- Page 128: In the second and third displays,
should be
.
- Page 129: “decaying faster” should be “decaying faster or having smaller amplitude”.
- Page 143: The proof that
is not correct as stated (the perturbations indicated do not preserve the property of being an
-flow). A correct argument is as follows. Call an edge of an
-flow unsaturated if it has weight strictly between 0 and
, and similarly call a vertex unsaturated if its net inflow or outflow is strictly less than
. Observe that if e is an unsaturated edge, then the final vertex u of e will either have an unsaturated edge leading out of it (if u is unsaturated) or another unsaturated edge leading into it (if u is saturated). Similarly, the initial vertex u’ of e will either have an unsaturated edge leading into it (if u is unsaturated) or another unsaturated edge leading out of it (if u is saturated). Thus, if there is at least one unsaturated edge, then by iterating the above observations, one can find an oriented cycle along unsaturated edges with the property that at any saturated vertex u, the number of edges flowing along the cycle into u equals the number of edges flowing against the cycle into u, and the number of edges flowing along the cycle out of u equals the number of edges flowing against the cycle out of u. For this cycle, one can modify the flow as indicated in the text to reduce the number of edges in the
-flow.
- Page 137: In the last line of Case 1, “multiply (1.47) by…” should be “raise (1.47) to the power
and then multiply by…”, and
should be
.
- Page 148: In the first line,
should read
.
- Page 180: In the second display,
should be
.
- Page 257: When selecting the large prime
, it is necessary that
is larger than 2. This is needed in order for the binomial expansion of
to be expressible in the desired form
where the polynomials
have coefficients in the p-adic integers, because the number of times
divides
can be bounded below by
, which goes to infinity as
provided that
is larger than 2.
- Page 267: In the third display,
should be
.
- Section 2.9.4: The application of the tensor power trick to the Riesz-Thorin theorem is only valid in the regime
.
- Section 2.10?: In (2.8),
should be
.
Thanks to Ravindra Bapat, Alan Chang, Dion, Norman Hardy, Matthew Kahle, Chris Kimmel, JamesL, Avi Levy, Russ Lyons, Arturo Magadin, Kirane Mokhtar, David P. Moulton, Kamil Rychlewicz , David Speyer, Caleb Stanford, Nikodem Szpak, Tobias and Tony, Chao Weng, Sheng-Peng Wu, and Yuncheng for corrections.


17 comments
Comments feed for this article
4 February, 2008 at 6:00 am
Prokrastination oder Blogroll (I): Terence Tao at LEMUREN-Blog
[…] Lässt man sich von den grösstenteils mathematisch anspruchsvollen Beiträgen, welche Tao nun in einem Buch zusammenfassen und veröffentlichen wird, so findet man dort neben Hinweisen zu “Career-Advice” und “On […]
6 August, 2008 at 6:02 am
the future of this blog | neverendingbooks
[…] I can see the point in setting up a blog connected to a book you once wrote or intend to write (such as Not Even Wrong or Terry Tao). […]
23 November, 2008 at 2:41 pm
Structure and Randomness: pages from year one of mathematical blog « What’s new
[…] AMS has just notified me that the book version of the first year of my blog, now retitled “Structure and Randomness: pages from year one of a mathematical blog“, is now available. An official web page for this book has also been set up here, though it […]
29 January, 2009 at 10:27 am
Poincaré’s legacies: pages from year two of a mathematical blog « What’s new
[…] in the previous book, those comments and corrections from readers which were of a substantive and mathematical nature […]
28 August, 2009 at 11:37 am
» Science 2.0: What Every Scientist Needs to Know About How the Web is Changing the Way They Work Information/Science
[…] Tao’s blog is professional enough that it has been formally published in two volumes: “Structure and Randomness: pages from year one of a mathematical blog” and “Poincaré’s legacies: pages from year two of a mathematical […]
8 February, 2010 at 2:27 pm
An epsilon of room: pages from year three of a mathematical blog « What’s new
[…] a mathematical blog“. It largely follows the format of my previous two blog books, “Structure and Randomness“ and “Poincaré’s […]
2 May, 2012 at 7:32 am
Arturo Magidin
I believe there is an error on page 95, Figure 1. The graph labeled as $K_{3,3}$ is not $K_{3,3}$, since the corner vertices are not connected to the opposite corners.
[Correction added, thanks – T.]
2 August, 2013 at 6:18 pm
Matt
I recently purchased this book in e-form through Google books – I was surprised that unlike the beautifully published print version, which I also own, Google appears to be selling a rather low-quality scanned version of your book, wrinkles visible, which is not searchable, text-reflow-able, nor available to read when not plugged into the internet. If I know mathematicians, I know that most would be appalled that their work was being presented, even sold, in such degraded form. Would you be kind enough to contact your publisher, AMS, and urge them to supply EPUB versions of your books to Google? This would be greatly appreciated, and I very much look forward to reading your articles on the subway without needing a wheelbarrow to carry the all the dead trees :) Thanks!
26 May, 2016 at 8:55 am
Kerri
Structure and randomness : where a simple law explodes into quantum elements of order that describe the bounds of physics. Where space is as important in understanding the order of structures as energy and matter is. These concepts are Real within Prime structure and pi, some of our favorite explorations of infinite possibility.
13 November, 2017 at 12:48 pm
Anonymous
There are a couple errors on pages 21-22. Propositions 1.8 and 1.10 are not correctly stated; a counterexample to both is
\epsilon = 4/5
k = 2
M = 4
x_1 = 0, x_2 = 0.1, x_3 = 0.9, x_4 = 1
The bound needed on M in Proposition 1.8 is stronger: $\lfloor\frac{M-1}{k}\rfloor \geq \epsilon$. Along the same lines, the bound needed on M in Proposition 1.10 is $\lfloor\log_2 (M) \rfloor$.
With these modifications, the proofs alluded to after each proposition do work. I suggest also changing $x_k, x_2k, x_3k, …$ to $x_1, x_{1+k}, x_{1+2k}, …$ on page 21 and removing the variable k from Proposition 1.10.
Thank you for the excellent article; I’m still working through it.
[Errata added, thanks – T.]
2 October, 2019 at 5:16 am
rongjiang pan
A Proof of Collatz Conjecture in Binary
https://github.com/ronaldpan/Collatz
21 January, 2024 at 8:33 am
Anonymous
Lemma: Union of a set of connected sets is again connected, if its intersection is non-empty.
Proof: If the set contains only one set, it is trivial. Otherwise, if one can split the union by using two disjoint open sets, then, by connectivity of each set, each set must choose its side. Now, if all of them choose to be on one side, then there is no split. So, some must be on one side, while some must be on the other. But then the intersection is empty.
Each point has its connected component. No two connected components can touch each other. Also, a clopen set and its complement constitute a pair of disjoint open sets.
Any clopen set is a union of connected components.
23 January, 2024 at 8:30 pm
Anonymous
Lemma: In ,
, ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) is a connected set.
is a connected set.
Proof: Suppose to the contrary, we can split the segment by a pair of disjoint (non-empty) open sets . So, we have
. So, we have  and
and 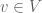 . Wlog, suppose
. Wlog, suppose  and
and  ,
, 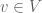 , consider the set
, consider the set ![S=\{x|[u,x]\subseteq U\}](https://s0.wp.com/latex.php?latex=S%3D%5C%7Bx%7C%5Bu%2Cx%5D%5Csubseteq+U%5C%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Set
. Set  . If
. If 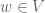 then for any
then for any  ,
, ![[w-\epsilon,w]](https://s0.wp.com/latex.php?latex=%5Bw-%5Cepsilon%2Cw%5D&bg=ffffff&fg=545454&s=0&c=20201002) must intersect
must intersect  so that
so that  cannot be open. If
cannot be open. If  then for any
then for any  ,
, ![[w,w+\epsilon]](https://s0.wp.com/latex.php?latex=%5Bw%2Cw%2B%5Cepsilon%5D&bg=ffffff&fg=545454&s=0&c=20201002) must intersect
must intersect  so that
so that  cannot be open.
cannot be open.
Corollary: In , every convex set is connected.
, every convex set is connected.
27 January, 2024 at 7:51 am
Anonymous
Claim: , where
, where  .
. is open and connected. Assume that some
is open and connected. Assume that some  continuously bijects
continuously bijects  and
and 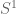 and that its inverse
and that its inverse 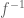 is continuous. Let
is continuous. Let  . It is fairly easy to see that
. It is fairly easy to see that  and
and  are disjoint and open in
are disjoint and open in  .
.  ,
,  are open in
are open in  . If none is empty,
. If none is empty,  ,
,  are disjoint open non-empty sets. Thus,
are disjoint open non-empty sets. Thus,  is disconnected. So some needs to be empty. If, for now, both are empty. In this case,
is disconnected. So some needs to be empty. If, for now, both are empty. In this case,  has cardinality
has cardinality  .
.  cannot biject
cannot biject  (containing just one element) to a unit circle
(containing just one element) to a unit circle 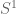 . It remains to falsify the last case wherein exactly one is empty. Wlog, assume
. It remains to falsify the last case wherein exactly one is empty. Wlog, assume  is empty. So,
is empty. So,  .
.
 is open and connected. Let
is open and connected. Let  . It is fairly easy to see that
. It is fairly easy to see that  and
and  are disjoint and open in
are disjoint and open in  .
.  ,
,  are open in
are open in  . If none is empty,
. If none is empty,  ,
,  are disjoint open non-empty sets. Thus,
are disjoint open non-empty sets. Thus,  is disconnected. So some needs to be empty. It cannot be the case that
is disconnected. So some needs to be empty. It cannot be the case that  is empty since
is empty since  belongs to it.
belongs to it.  must be empty. So,
must be empty. So,  .
. . Still in the last case, we notice that yet another set, namely,
. Still in the last case, we notice that yet another set, namely,  is open and connected. Let
is open and connected. Let  . As before, define
. As before, define  and
and  . Some needs to be empty by the same argument. Since
. Some needs to be empty by the same argument. Since  and
and  , none can be empty.
, none can be empty. . Or, all of your computability-theory related papers can be well understood.
. Or, all of your computability-theory related papers can be well understood.
Proof:
What we have obtained so far is
Now take this as a gift
10 February, 2024 at 10:53 pm
T Retsu
Buhrman communicated the following theorem to Fortnow.
Theorem 15: .
. parallel-querying oracle machine
parallel-querying oracle machine  and for each
and for each  let
let 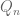 be the union of the set of all queries to
be the union of the set of all queries to  made by
made by  on all
on all  of length
of length  . Our advice
. Our advice  is
is  .
.
Proof: Given an
Our machine on input
machine on input  and advice
and advice  works as follows:
works as follows:
– Compute : enumerate through all
: enumerate through all  (including
(including  certainly), compute the set of parallel queries made by
certainly), compute the set of parallel queries made by 
 formulae out of
formulae out of  , each with an assignment.
, each with an assignment.
– Guess exactly
– For each guessed formula, verify that its guessed assignment is satisfying. (If any guess is wrong, reject and halt)
Well, all guesses are correct and we now have all the information needed to smoothly simulate answering the queries (yes if it is in the
answering the queries (yes if it is in the  guessed formulae, no otherwise). Accept or reject just as the deterministic
guessed formulae, no otherwise). Accept or reject just as the deterministic  (at the end of each long non-deterministic branch till now).■
(at the end of each long non-deterministic branch till now).■
A computational perspective of mathematics as a happy new lunar year wish!
17 February, 2024 at 11:13 am
T Retsu
Fortnow-Santhanam-Williams have quite an interesting theorem in their paper joint “Fixed-Polynomial Size Circuit Bounds”.
Theorem 14: For all , for all
, for all  , if
, if ![\mathrm{P}^\mathrm{NP}[n^c]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BP%7D%5E%5Cmathrm%7BNP%7D%5Bn%5Ec%5D&bg=ffffff&fg=545454&s=0&c=20201002) has
has  -size circuits, then
-size circuits, then ![\mathrm{NTIME}[n^{c-0.0000000001}]\subseteq\mathrm{MATIME}[n^k\mathrm{polylog}(n)]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BNTIME%7D%5Bn%5E%7Bc-0.0000000001%7D%5D%5Csubseteq%5Cmathrm%7BMATIME%7D%5Bn%5Ek%5Cmathrm%7Bpolylog%7D%28n%29%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
9 March, 2024 at 7:04 pm
Anonymous
S.Dolan has a very interesting article on The Mathematical Gazette of CambridgeUP:
105.38 A very simple proof of the two-squares theorem