I’ve just uploaded to the ArXiV my paper “Norm convergence of multiple ergodic averages for commuting transformations“, submitted to
Ergodic Theory and Dynamical Systems. This paper settles in full generality the norm convergence problem for several commuting transformations. Specifically, if is a probability space and
are commuting measure-preserving transformations, then for any bounded measurable functions
, the multiple average
(1)
is convergent in the norm topology (and thus also converges in probability). The corresponding question of pointwise almost everywhere convergence remains open (and quite difficult, in my opinion). My argument also does not readily establish a formula as to what this limit actually is (it really establishes that the sequence is Cauchy in
rather than convergent).
The l=1 case of this theorem is the classical mean ergodic theorem (also known as the von Neumann ergodic theorem). The l=2 case was established by Conze and Lesigne. The higher l case was partially resolved by Frantzikinakis and Kra, under the additional hypotheses that all of the transformations , as well as the quotients
, are ergodic. The special case
was established by Host-Kra (with another proof given subsequently by Ziegler). Another relevant result is the Furstenberg-Katznelson theorem, which asserts among other things when
is non-negative and not identically zero, then the inner product of the expression (1) with f has a strictly positive limit inferior as
. This latter result also implies Szemerédi’s theorem.
It is also known that the Furstenberg-Katznelson theorem can be proven by hypergraph methods, and in fact my paper also proceeds by a hypergraph-inspired approach, although the language of hypergraphs is not explicitly used in the body of the argument. (In contrast to the work of Host-Kra and Ziegler, no nilsystems appear in the proof.)
In fact, the first step in the argument is to replace the infinitary norm convergence result by an equivalent finitary norm convergence result, in exactly the same way that the infinite convergence principle is equivalent to the finite convergence principle. (This is in marked contrast with the usual ergodic-theory approach to these problems, in which one tries to prove the infinitary statement first, by purely infinitary means, and only deduces the finitary counterpart as a corollary at the very end of the argument.) In the finitary counterpart of this norm convergence result, the abstract dynamical system X is replaced by a very concrete one, namely the product of l cyclic groups, with the standard set of l commuting shifts. The main advantage of this concrete setting is that it has an obvious Cartesian product structure, which lets one interpret the functions
as weighted hypergraphs, and which allows the technology of the hypergraph regularity lemma to be applied. (Actually we will only need a weak version of this lemma, similar to the “Koopman-von Neumann-type theorems” that appear for instance in my work with Ben on arithmetic progressions of primes, or to the weak regularity lemma of Frieze and Kannan.)
Roughly speaking, the idea is now to induct on the “complexity” of the functions . Informally, a function f on, say,
(actually for technical reasons we use
) is of complexity d if it only depends of d of the coordinates, or if it is a polynomial combination of such functions (with quantitative bounds on the polynomial involved). The regularity lemma allows one to approximate a complexity d function by a complexity d-1 function, plus an error which is sufficiently “pseudorandom” or “uniform” to be negligible for the purposes of the norm convergence problem. We iterate this all the way down to d=1, at which point one is at the level of the mean ergodic theorem and one can proceed by a variety of methods.
One amusing side-effect of the finitary nature of the argument was that I needed a finitary version of the Lebesgue dominated convergence theorem, which I include as an appendix. Actually, one does not strictly speaking need this theorem to run the argument, if one is willing to add a little bit more notation instead, but the finitary convergence theorem may be of some independent interest.
While the methods in the paper are finitary, it seems likely that a more traditional infinitary ergodic proof of this theorem should be possible (once one figures out how to obtain the counterpart of Cartesian product structure in the infinitary setting). It would thus be interesting to obtain a second proof of this result.

19 comments
Comments feed for this article
11 July, 2007 at 3:59 pm
Top Posts « WordPress.com
[…] Norm convergence of multiple ergodic averages for commuting transformations I’ve just uploaded to the ArXiV my paper “Norm convergence of multiple ergodic averages for commuting […] […]
11 July, 2007 at 6:00 pm
Peter McNamara
Terry,
I was wondering about the role of the assumption of commutativity that the transformations in this paper, and in the Furstenberg-Katznelson theorem are assumed to satisfy. Firstly, is there a simple example showing the necessity of this commutativity assumption? And secondly, can anything be salvaged if this assumption is dropped? I cannot hazard much of a guess having not looked in any detail at the arguments involved.
Peter
12 July, 2007 at 4:52 pm
Terence Tao
Dear Peter,
The Furstenberg-Katznelson theorem holds if the shifts generate a nilpotent group, but not if they generate just a solvable group or worse. See
A. Leibman, Multiple recurrence theorem for nilpotent group actions, Geom. and Func. Anal. 4 (1994), 648-659.
and
V. Bergelson, A. Leibman, Failure of Roth theorem for solvable groups of exponential growth, Ergodic Theory and Dynam. Systems 24 (2004), 45–53.
In my own paper, the commutativity was used to move the problem to one in the lattice , at which point one can use a simple arithmetic substitution to convert the problem into a hypergraph one. I suspect that something similar can also be done in the nilpotent case. A good test problem would be to reprove the norm convergence for multiple polynomial powers of a single shift by these methods (this was shown recently by Frantzikinakis-Kra using nilsystems).
, at which point one can use a simple arithmetic substitution to convert the problem into a hypergraph one. I suspect that something similar can also be done in the nilpotent case. A good test problem would be to reprove the norm convergence for multiple polynomial powers of a single shift by these methods (this was shown recently by Frantzikinakis-Kra using nilsystems).
14 July, 2007 at 5:13 am
Zaiaku
[…] Norm convergence of multiple ergodic averages for commuting transformations I’ve just uploaded to the ArXiV my paper “Norm convergence of multiple ergodic averages for commuting […] […]
10 August, 2007 at 12:27 pm
Henry Towsner
I’ve been thinking about what an infinitary version of the argment would look like, and put up a short outline of an infinitary analog of this proof:
Click to access NormConvergence.pdf
Some of the features–in particular, the passage from an average to an integral (which, in the infinitary version, seems to require a generalized form of the Furstenberg correspondence)–look like they might be independently interesting.
Henry
10 August, 2007 at 7:59 pm
Terence Tao
Dear Henry,
Very nice (and quick)! I am happy to see the Furstenberg correspondence principle being developed in both directions; we usually use it as a narrow bridge between the finitary and infinitary worlds when it really should be a six-lane freeway :-). As usual, things get a lot cleaner in the infinitary world with most of the epsilons and other parameters being efficiently hidden from sight.
The main reason I couldn’t get anywhere in the infinitary world was the lack of a product structure, which is why I descended back to the finitary world. But it’s good to see that the same product structure can also be now recovered in the infinitary setting, even if it is a little odd to have to go back and forth across the Furstenberg correspondence to do so.
12 August, 2007 at 8:37 pm
Terence Tao
p.s. It occurs to me that the product Furstenberg correspondence principle you discovered may help elucidate an odd little phenomenon I observed in appendix B of one of my papers:
http://front.math.ucdavis.edu/math.CO/0602037
It is known that the Furstenberg recurrence theorem in ergodic theory is equivalent (via the correspondence principle) to Szemeredi’s theorem, which is a consequence of a hypergraph removal lemma. In the above paper I deduce the latter lemma from an infinitary analogue, showing that certain systems of sigma algebras obey a “uniform intersection property”. I was always a bit dissatisfied by this passage back and forth between the finitary and infinitary worlds; in particular, there should be a direct way to establish the Furstenberg recurrence theorem (or the more general Furstenberg-Katznelson multidimensional recurrence theorem) from the uniform intersection property, but I was not able to do this in an elegant way in the appendix. Perhaps the new correspondence principle can sort this out a bit better…
15 August, 2007 at 8:59 am
Henry Towsner
Where I used the product construction, the only issue was splitting up the commuting transformations to be independent from each other. The embedding into tripartite graphs uses sums, so it isn’t automatic that the same technique will work, although it’s certainly possible. I’m having a bit of trouble working through appendix B (in particular, I’m not following the definitions of E_23 and E_31; for instance, the definition of E_23 makes reference to the parameter k_1, and I’m not clear what k_1 refers to in this definition).
Which reminds me that there was one step in your norm convergence paper I didn’t follow: you say that ||Delta_N h||_1<=||h||_1, but it’s not obvious to me why this is the case, since ||h||_1 includes all the “off-diagonal” parts of h, which collectively have measure (approaching) 1.
15 August, 2007 at 9:37 am
Terence Tao
Oops, that is a typo in Appendix B. in ,
,  should be
should be 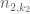 , and in
, and in 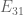 ,
, 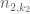 should be
should be  . (Ugh.)
. (Ugh.)
As for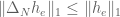 , one has to use the fact that
, one has to use the fact that 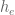 is e-measurable for some e which is strictly smaller than {1,…,l+1} but contains l+1, so that the diagonal is nicely transverse to the sigma-algebra of
is e-measurable for some e which is strictly smaller than {1,…,l+1} but contains l+1, so that the diagonal is nicely transverse to the sigma-algebra of 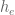 . Indeed, one can then check for any n that the function
. Indeed, one can then check for any n that the function 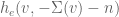 has exactly the same L^1 norm as
has exactly the same L^1 norm as  (due to the ability to “move” arbitrarily in some index i in {1,…,l} \ e, which renders the constraint
(due to the ability to “move” arbitrarily in some index i in {1,…,l} \ e, which renders the constraint  ineffectual), and the contraction property then follows from Minkowski’s inequality.
ineffectual), and the contraction property then follows from Minkowski’s inequality.
4 September, 2007 at 11:48 am
Henry Towsner
After looking for a while, I think some additional idea would be needed to handle the additive structure in the hypergraph setup. The construction I used in my notes doesn’t seem flexible enough to handle that directly.
Also, I have another question about your paper. For d>1, are there any uniform functions with large L^2 norm? In the infinitary case, it seems that there shouldn’t be (every function is in the L^2 limit of the complexity 1, and therefore complexity 2 anti-uniform, functions, since this is essentially the definition of the product structure). But if this is right, it seems to give a proof that avoids the inductive step: after proving the case for d=1, any g_e can be decomposed into the sum of a complexity 1 function and a function with small L^2 norm, using the general properties of the product, withou the need for a Koopman-von Neumann type decomposition. Then prod g_e can be decomposed into pieces in which either some element of the product has small norm (ensuring that the entire product does as well), or have complexity 1 (immediately, without needing to pass through the anti-uniform functions), and a product of complexity 1 functions is already known to converge.
4 September, 2007 at 12:55 pm
Terence Tao
Dear Henry,
There are definitely uniform functions of any order with large L^2 norm, for instance consider a random function f on Z_P^l which equals +1 or -1 at each element of Z_P^l with equal and independent probability. Then this function f is large in L^2, but a simple computation using the Chernoff inequality and the union bound shows that with very high probability, f is going to have a very small inner product against all products of functions of l-1 of the l variables. (Basically, there are only about exp( O( P^{l-1} ) ) of these functions that one has to consider, but for each such function one is going to have a small inner product with f with a probability like exp( – c P^l ) for some c > 0, and so the union bound is going to be favourable.)
One has to be a little cautious here when extrapolating intuition about measurability from the infinite world to the finite world. It is true that every measurable function in a product space can be approximated by a linear combination of measurable functions in the factor spaces; however, there is no quantitative bound as to how complex a combination one needs in order to obtain a desired level of approximation; one needs quantitative bounds on the complexity in order to obtain a meaningful finitary world. In the finitary world, random functions such as the one I described above are, technically speaking, measurable, but they are very high complexity, and are indeed essentially orthogonal to all low-complexity (or anti-uniform) objects.
Incidentally, there was a slight error in Section 2 of my paper; I cannot require my generic point x_0 to witness the ergodic theorem (equation (3)) for every f in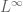 (and in fact the equation doesn’t make sense for such f, since they are only defined up to almost everywhere equivalence). But one only needs (3) to be true for functions which are polynomial combinations of the original functions
(and in fact the equation doesn’t make sense for such f, since they are only defined up to almost everywhere equivalence). But one only needs (3) to be true for functions which are polynomial combinations of the original functions  with rational coefficients, so there is no difficulty. (Alternatively, one can place a topology on X and require f_1,…,f_l to be continuous.) But your own writeup may need some adjusting to fix the same problem.
with rational coefficients, so there is no difficulty. (Alternatively, one can place a topology on X and require f_1,…,f_l to be continuous.) But your own writeup may need some adjusting to fix the same problem.
5 September, 2007 at 9:00 am
John Griesmer
Henry,
Indeed, your Lemma 2.1 gives the desired convergence as a consequence of convergence in the complexity one case. It also gives the multiple recurrence theorems of Szemerédi and Furstenberg-Katznelson as a consequence of the Poincaré
recurrence theorem. I can elaborate if you like.
6 September, 2007 at 12:46 pm
Henry Towsner
John,
I’m afraid it looks Lemma 2.1 has all these powerful consequences because it isn’t true. Tim Austin has pointed out that the argument I gave has a significant gap, and it looks like it can’t be patched without weakening the lemma. I’m looking into how to weaken it to something true, but anything true shouldn’t have consequences nearly so strong. (Indeed, it should be just enough to justify an infinitary version of Tao’s original argument.)
17 October, 2007 at 11:50 am
Henry Towsner
I believe I’ve repaired the infinitary version, and posted a new draft at
Click to access NormConvergence.pdf
It uses a weaker structure theorem, taking the original space and passing to an extension of a product space with an additional technical property. Unfortunately, I haven’t found any way to obtain this other than with a Loeb measure argument.
30 January, 2008 at 6:52 pm
254A, Lecture 8: The mean ergodic theorem « What’s new
[…] for commuting shifts , which does not seem possible using the other arguments given here; see this paper of mine for details. Further quantitative analysis of the mean ergodic theorem can be found in this paper […]
31 August, 2008 at 4:09 pm
The correspondence principle and finitary ergodic theory « What’s new
[…] This is of course a well-known result with many short and elegant proofs; the proof method that we sketch here (essentially due to Avigad, Gerhardy, and Towsner) is lengthier and messier than the purely infinitary proofs, but can be extended to some situations in which it had been difficult to proceed in an infinitary manner (in particular on my result on convergence for multiple commuting transformations, as discussed in this post of mine). […]
30 November, 2008 at 8:39 am
254A, Lecture 10: The Furstenberg correspondence principle « What’s new
[…] a (rather complicated looking) finitary analogue; see the papers of Avigad-Gerhardy-Towsner and of myself on this subject. Finally, we have implicitly been using a similar correspondence principle between […]
25 October, 2012 at 10:10 am
Walsh’s ergodic theorem, metastability, and external Cauchy convergence « What’s new
[…] strengthens and generalises a number of previous convergence results in ergodic theory (including one of my own), with a remarkably simple proof. Walsh’s argument is phrased in a finitary language […]
11 December, 2013 at 10:31 am
Convergence and Recurrence of Z actions | I Can't Believe It's Not Random!
[…] any such that . The convergence result associated with this result was establish by Tao in 2007, after some particular cases by Conze and Lesigne, and states that the […]