In this lecture, we describe the simple but fundamental Furstenberg correspondence principle which connects the “soft analysis” subject of ergodic theory (in particular, recurrence theorems) with the “hard analysis” subject of combinatorial number theory (or more generally with results of “density Ramsey theory” type). Rather than try to set up the most general and abstract version of this principle, we shall instead study the canonical example of this principle in action, namely the equating of the Furstenberg multiple recurrence theorem with Szemerédi’s theorem on arithmetic progressions.
In 1975, Szemerédi established the following theorem, which had been conjectured in 1936 by Erdős and Turán:
Theorem 1. (Szemerédi’s theorem) Let
be an integer, and let A be a set of integers of positive upper density, thus
. Then A contains a non-trivial arithmetic progression
of length k. (By “non-trivial” we mean that
.) [More succinctly: every set of integers of positive upper density contains arbitrarily long arithmetic progressions.]
This theorem is trivial for k=1 and k=2. The first non-trivial case is k=3, which was proven by Roth in 1953 and will be discussed in a later lecture. The k=4 case was also established by Szemerédi in 1969.
In 1977, Furstenberg gave another proof of Szemerédi’s theorem, by establishing the following equivalent statement:
Theorem 2. (Furstenberg multiple recurrence theorem) Let
be an integer, let
be a measure-preserving system, and let E be a set of positive measure. Then there exists
such that
is non-empty.
Remark 1. The negative signs here can be easily removed because T is invertible, but I have placed them here for consistency with some later results involving non-invertible transformations, in which the negative sign becomes important.
Exercise 1. Prove that Theorem 2 is equivalent to the apparently stronger theorem in which “is non-empty” is replaced by “has positive measure”, and “there exists ” is replaced by “there exist infinitely many
“.
Note that the k=1 case of Theorem 2 is trivial, while the k=2 case follows from the Poincaré recurrence theorem (Theorem 1 from Lecture 8). We will prove the higher k cases of this theorem in later lectures. In this one, we will explain why, for any fixed k, Theorem 1 and Theorem 2 are equivalent.
Let us first give the easy implication that Theorem 1 implies Theorem 2. This follows immediately from
Lemma 1. Let
be a measure-preserving system, and let E be a set of positive measure. Then there exists a point x in X such that the recurrence set
has positive upper density.
Indeed, from Lemma 1 and Theorem 1, we obtain a point x for which the set contains an arithmetic progression of length k and some step r, which implies that
is non-empty.
Proof of Lemma 1. Observe (from the shift-invariance of ) that
. (1)
On the other hand, the integrand is at most 1. We conclude that for each N, the set must have measure at least
. This implies that the function
is not absolutely integrable even after excluding an arbitrary set of measure up to
, which implies that
is not finite a.e., and the claim follows (cf. the proof of the Borel-Cantelli lemma).
Now we show how Theorem 2 implies Theorem 1. If we could pretend that “upper density” was a probability measure on the integers, then this implication would be immediate by applying Theorem 2 to the dynamical system . Of course, we know that the integers do not admit a shift-invariant probability measure (and upper density is not even additive, let alone a probability measure). So this does not work directly. Instead, we need to first lift from the integers to a more abstract universal space and use a standard “compactness and contradiction” argument in order to be able to build the desired probability measure properly.
More precisely, let A be as in Theorem 1. Consider the topological boolean Bernoulli dynamical system with the product topology and the shift
. The set A can be viewed as a point in this system, and the orbit closure
of that point becomes a subsystem of that Bernoulli system, with the relative topology.
Suppose for contradiction that A contains no non-trivial progressions of length k, thus for all
. Then, if we define the cylinder set
to be the collection of all points in X which (viewed as sets of integers) contain 0, we see (after unpacking all the definitions) that
for all
.
In order to apply Theorem 2 and obtain the desired contradiction, we need to find a shift-invariant Borel probability measure on X which assigns a positive measure to E.
For each integer N, consider the measure which assigns a mass of
to the points
in X for
, and no mass to the rest of X. Then we see that
. Thus, since A has positive upper density, there exists some sequence
going to infinity such that
. On the other hand, by vague sequential compactness (Lemma 1 of Lecture 7) we know that some subsequence of
converges in the vague topology to a probability measure
, which then assigns a positive measure to the (clopen) set E. As the
are asymptotically shift invariant, we see that
is invariant also (as in the proof of Corollary 1 of Lecture 7). As
now has all the required properties, we have completed the deduction of Theorem 1 from Theorem 2.
Exercise 2. Show that Theorem 2 in fact implies a seemingly stronger version of Theorem 1, in which the conclusion becomes the assertion that the set has positive upper density for infinitely many r.
Exercise 3. Show that Theorem 1 in fact implies a seemingly stronger version of Theorem 2: If are sets in a probability space with uniformly positive measure (i.e.
), then for any k there exists positive integers n, r such that
.
— Varnavides type theorems —
A similar “compactness and contradiction” argument (combined with a preliminary averaging-over-dilations trick of Varnavides) allows us to use Theorem 2 to imply the following apparently stronger statement (observed by Bergelson, Host, McCutcheon, and Parreau):
Theorem 3. (Uniform Furstenberg multiple recurrence theorem) Let
be an integer and
. Then for any measure-preserving system
and any measurable set E with
we have
(2)
for all
, where
is a positive quantity which depends only on k and
(i.e. it is uniform over all choices of system and of the set E with measure at least
).
Exercise 4. Assuming Theorem 3, show that if N is sufficiently large depending on k and , then any subset of
with cardinality at least
will contain at least
non-trivial arithmetic progressions of length k, for some
. (This result for k=3 was first established by Varnavides via an averaging argument from Roth’s theorem.) Conclude in particular that Theorem 3 implies Theorem 1.
It is clear that Theorem 3 implies Theorem 2; let us now establish the converse. We first use an averaging argument of Varnavides to reduce Theorem 3 to a weaker statement, in which the conclusion (2) is not asserted to hold for all N, but instead one asserts that
(2′)
is true for some depending only on k and
(note that the r=0 term in (2′) has been dropped, otherwise the claim is trivial). To see why one can recover (2) from (2′), observe by replacing the shift T with a power
that we can amplify (2′) to
(2”)
for all a. Averaging (2”) over we easily conclude (2).
It remains to prove that (2”) holds under the hypotheses of Theorem 3. Our next reduction is to observe that for it suffices to perform this task for the boolean Bernoulli system with the cylinder set
as before. To see this, recall from Example 5 of Lecture 2 that there is a morphism
from any measure-preserving system
with a distinguished set E to the system
with the product
-algebra
, the usual shift
, and the set
, and with the push-forward measure
. Specifically,
sends any point x in X to its recurrence set
. Using this morphism it is not difficult to show that the claim (2) for
and E would follow from the same claim for
and
.
We still need to prove (2”) for the boolean system. The point is that by lifting to this universal setting, the dynamical system and the set E have been canonically fixed; the only remaining parameter is the probability measure
. But now we can exploit vague sequential compactness again as follows.
Suppose for contradiction that Theorem 3 failed for the boolean system. Then by carefully negating all the quantifiers, we can find such that for any
there is a sequence of shift-invariant probability measures
on X with
,
(3)
as . Note that if (3) holds for one value of
, then it also holds for all smaller values of
. A standard diagonalisation argument then allows us to build a sequence
as above, but which obeys (3) for all
.
Now we are finally in a good position to apply vague sequential compactness. By passing to a subsequence if necessary, we may assume that converges vaguely to a limit
, which is a shift-invariant probability measure. In particular we have
, while from (3) we see that
(4)
for all ; thus the sets
all have zero measure for
. But this contradicts Theorem 2 (and Exercise 1). This completes the deduction of Theorem 3 from Theorem 2.
— Other recurrence theorems and their combinatorial counterparts —
The Furstenberg correspondence principle can be extended to relate several other recurrence theorems to their combinatorial analogues. We give some representative examples here (without proofs). Firstly, there is a multidimensional version of Szemerédi’s theorem (compare with Exercise 7 from Lecture 4):
Theorem 4 (Multidimensional Szemerédi theorem) Let
, let
, and let
be a set of positive upper Banach density (which means that
, where
). Then A contains a pattern of the form
for some
and
.
Note that Theorem 1 corresponds to the special case when and
.
This theorem was first proven by Furstenberg and Katznelson, who deduced it via the correspondence principle from the following generalisation of Theorem 2:
Theorem 5 (Recurrence for multiple commuting shifts) Let
be an integer, let
be a probability space, let
be measure-preserving bimeasurable maps which commute with each other, and let E be a set of positive measure. Then there exists
such that
is non-empty.
Exercise 5. Show that Theorem 4 and Theorem 5 are equivalent.
Exercise 6. State an analogue of Theorem 3 for multiple commuting shifts, and prove that it is equivalent to Theorem 5.
There is also a polynomial version of these theorems (cf. Theorem 1 from Lecture 5), which we will also state in general dimension:
Theorem 6 (Multidimensional polynomial Szemerédi theorem) Let
, let
be polynomials with
, and let
be a set of positive upper Banach density. Then A contains a pattern of the form
for some
and
.
This theorem was established by Bergelson and Leibman, who deduced it from
Theorem 7 (Polynomial recurrence for multiple commuting shifts) Let k,
,
, E be as in Theorem 5, and let
be as in Theorem 6. Then there exists
such that
is non-empty, where we adopt the convention
(thus we are making the action of
on X explicit).
Exercise 7. Show that Theorem 6 and Theorem 7 are equivalent.
Exercise 8. State an analogue of Theorem 3 for polynomial recurrence for multiple commuting shifts, and prove that it is equivalent to Theorem 7. (Hint: first establish this in the case that each of the are monomials, in which case there is enough dilation symmetry to use the Varnavides averaging trick. Interestingly, if one only restricts attention to one-dimensional systems k=1, it does not seem possible to deduce the uniform polynomial recurrence theorem from the non-uniform polynomial recurrence theorem, thus indicating that the averaging trick is less universal in its applicability than the correspondence principle.)
In the above theorems, the underlying action was given by either the integer group or the lattice group
. It is not too difficult to generalise these results to the semigroups
and
(thus dropping the assumption that the shift maps are invertible), by using a trick similar to that used in Exercise 9 of Lecture 4, or by using the correspondence principle back and forth a few times. A bit more surprisingly, it is possible to extend these results to even weaker objects than semigroups. To describe this we need some more notation.
Define a partial semigroup to be a set G together with a partially defined multiplication operation
for some subset
, which is associative in the sense that whenever
is defined, then
is defined and equal to
, and vice versa. A good example of a partial semigroup is the finite subsets
of a fixed set S, where the multiplication operation
is disjoint union, or more precisely
when A and B are disjoint, and
is undefined otherwise.
Remark 2. One can extend a partial semigroup to be a genuine semigroup by adjoining a new element to G, and redefining multiplication
to equal
if it was previously undefined (or if one of a or b was already equal to
). However, we will avoid using this trick here, as it tends to complicate the notation a little.
One can take Cartesian products of partial semigroups in the obvious manner to obtain more partial semigroups. In particular, we have the partial semigroup for any
, defined as the collection of d-tuples
of finite sets of natural numbers (not necessarily disjoint), with the partial semigroup law
whenever
and
are disjoint for each
.
If is a probability space and
is a partial semigroup, we define a measure-preserving action of G on X to be an assignment of a measure-preserving transformation
(not necessarily invertible) to each
, such that
whenever
is defined.
An action T of on X is known as an IP system on X; it is generated by a countable number
of commuting measure-preserving transformations, with
. (Admittedly, it is possible that the action of the empty set is not necessarily the identity, but this turns out to have a negligible impact on matters.) An action T of
is then a collection of d simultaneously commuting IP systems.
Furstenberg and Katznelson showed the following generalisation of Theorem 5:
Theorem 8 (IP multiple recurrence theorem) Let T be an action of
on a probability space
. Then there exists a non-empty set
such that
is non-empty, where
is the group element which equals A in the
position and is the empty set otherwise.
It has a number of combinatorial consequences, such as the following strengthening of Szemerédi’s theorem:
Theorem 9. (IP Szemerédi theorem) Let A be a set of integers of positive upper density, let
, and let
be infinite. Then A contains an arithmetic progression
of length k in which r lies in FS(B), the set of finite sums of B (cf. Hindman’s theorem from Lecture 5).
(There is also a multidimensional version of this theorem, but it requires a fair amount of notation to state properly.)
Exercise 9. Deduce Theorem 9 from Theorem 8.
Exercise 10. Using Theorem 9, show that for any k, and any set of integers A of positive upper density, the set of steps r which occur in the arithmetic progressions in A of length k is syndetic.
Exercise 11. Using Theorem 8, show that if is a finite field, and
is the canonical vector space over
spanned (in the algebraic sense) by a countably infinite number of basis vectors, show that any subset A of
of positive upper Banach density (which means that
contains affine subspaces of arbitrarily high dimension.
The IP recurrence theorem is already very powerful, but even stronger theorems are known. For instance, Furstenberg and Katznelson established the following deep strengthening of the Hales-Jewett theorem (Theorem 8 from Lecture 5), as well as of Exercise 11 above:
Theorem 10 (Density Hales-Jewett theorem) Let A be a finite alphabet. If E is a subset of
of positive upper Banach density, then E contains a combinatorial line.
This theorem was deduced (via an advanced form of the correspondence principle) by a somewhat complicated recurrence theorem which we will not state here; rather than the action of a group, semigroup, or partial semigroup, one instead works with an ensemble of sets (as in Exercise 3), and furthermore one regularises the system of the probability space and set ensemble (which can collectively be viewed as a random process) to be what Furstenberg and Katznelson call a strongly stationary process, which (very) roughly means that the statistics of this process look “the same” when restricted to any combinatorial subspace of a fixed dimension.
Remark 3. Similar correspondence principles can be established connecting property testing results for graphs and hypergraphs to the measure theory of exchangeable measures: see this paper of myself, and of myself and Austin, for details. There is also a correspondence principle connecting ergodic convergence theorems with a (rather complicated looking) finitary analogue; see the papers of Avigad-Gerhardy-Towsner and of myself on this subject. Finally, we have implicitly been using a similar correspondence principle between topological dynamics and colouring Ramsey theorems in our previous lectures (in particular Lecture 3, Lecture 4, and Lecture 5).
Remark 4. The Furstenberg correspondence principle also comes tantalisingly close to deducing my theorem with Ben that the primes contain arbitrarily long arithmetic progressions from Szemerédi’s theorem. More precisely, they show that any subset A of a genuinely random set of integers with logarithmic-type density B, with A having positive relative upper density with respect to B, contains arbitrarily long arithmetic progressions; see this unpublished note of myself. Unfortunately, the almost primes are not known to quite obey enough “correlation conditions” to behave sufficiently pseudorandomly that these arguments apply to the primes, though perhaps there is still a “softer” way to prove our theorem than the way we did it (there is for instance some recent work by Trevisan, Tulsiani, and Vadhan in this direction).

26 comments
Comments feed for this article
11 February, 2008 at 9:14 pm
254A, Lecture 11: Compact systems « What’s new
[…] and the next few will be to give a proof of the Furstenberg recurrence theorem (Theorem 2 from the previous lecture). Along the way we will develop a structural theory for measure-preserving […]
22 February, 2008 at 2:39 pm
254A, Lecture 12: Weakly mixing systems « What’s new
[…] can then immediately establish the k=3 case of Furstenberg’s theorem (Theorem 2 from Lecture 10) by combining the above result with the ergodic decomposition (Proposition 4 from Lecture 9). The […]
1 March, 2008 at 11:05 pm
254A, Lecture 13: Compact extensions « What’s new
[…] those spaces X which are regular, though an inspection of the Furstenberg correspondence principle (Lecture 10) shows that this is in fact automatic for the purposes of such tasks as proving Szemerédi’s […]
1 March, 2008 at 11:05 pm
254A, Lecture 13: Compact extensions « What’s new
[…] those spaces X which are regular, though an inspection of the Furstenberg correspondence principle (Lecture 10) shows that this is in fact automatic for the purposes of such tasks as proving Szemerédi’s […]
2 July, 2008 at 9:30 pm
Szemeredi’s theorem « Abner’s Postgraduate Days
[…] 254A, Lecture 10: The Furstenberg correspondence principle […]
29 November, 2008 at 6:05 am
liuxiaochuan
dear Professor Tao:
I have several questions(or corrections).
1, In the proof of Lemma 1, I didn’t get how the Borel-Cantelli lemma are used. I only tried to prove it from definition of upper limit of sets.
2, In exercise 4, I think is too large for the lemma to be correct. Anyway, I can only do it with
is too large for the lemma to be correct. Anyway, I can only do it with  .
.
3,In the proof of Theorem 3, the first sentences of two paragraphs after (2”), it should be “It remains to prove that (2”) holds” and “We still need to prove (2”) for”, not (2)
4,In both the statement of theorem 4 and theorem 6, A should be a set of positive upper Banach density, “positive” missing.
29 November, 2008 at 9:04 am
Terence Tao
Dear liuxiaochuan,
Thanks for the corrections! It’s true that Lemma 1 doesn’t directly use the Borel-Cantelli lemma, but the method of proof is similar (one analyses the sum of indicator functions of the sets involved).
For exercise 4, the trick is to take advantage of both the translation invariance and dilation invariance in the space of arithmetic progressions: using only one of these symmetries will only give the bound of , but you need both to get
, but you need both to get  . For this purpose it can be convenient to to embed
. For this purpose it can be convenient to to embed 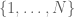 into a slightly larger cyclic group, e.g. one of prime order, although this is not strictly necessary (e.g. Varnavides’ original argument did not do this).
into a slightly larger cyclic group, e.g. one of prime order, although this is not strictly necessary (e.g. Varnavides’ original argument did not do this).
29 November, 2008 at 9:48 pm
liuxiaochuan
Dear Professor Tao:
About 4, I think I finally get it. Thanks.
By the way, in theorem 6, A is a set of positive upper Banach density, “positive” still missing.
5 October, 2009 at 3:50 am
Ergodic Ramsey Theory (by Yuri Lima) « Disquisitiones Mathematicae
[…] 3. Furstenberg’s Correspondence Principle. […]
14 December, 2009 at 1:51 pm
ERT4: Multiple Ergodic Averages « Disquisitiones Mathematicae
[…] we’ll see in forecoming posts, this actually proves Szemerédi’s Theorem, via a correspondence principle between sets of integers of positive density and measure-preserving systems. One year after, […]
25 March, 2010 at 11:44 pm
Theorem 22: Szemeredi’s theorem « Theorem of the week
[…] to have nothing to do with a combinatorial problem). In particular, he developed the Furstenberg correspondence principle, and this and related ideas have led to many proofs of other results, including some that seemed […]
23 May, 2010 at 8:38 pm
Solutions to Ergodic Theory: Lecture ten « Xiaochuan Liu's Weblog
[…] Note: Professor Terence Tao Began posting his lecture notes about the course “ergodic theory” early in 2008. I try doing all the exercises. This is the eleven exercises in lecture two. Here is the the page of this course,and here is the page of this lecture. […]
25 July, 2010 at 8:23 am
Yiannis
hi — small typo (?) in the statement of Lemma 1: do you want $x\in E$ instead of $x\in X$?
23 January, 2011 at 7:13 am
The Peter-Weyl theorem, and non-abelian Fourier analysis on compact groups « What’s new
[…] I’ve recently become interested in the theory around Hilbert’s fifth problem, due to the existence of a correspondence principle between locally compact groups and approximate groups, which play a fundamental role in arithmetic combinatorics. I hope to elaborate upon this correspondence in a subsequent post, but I will mention that versions of this principle play a crucial role in Gromov’s proof of his theorem on groups of polynomial growth (discussed previously on this blog), and in a more recent paper of Hrushovski on approximate groups (also discussed previously). It is also analogous in many ways to the more well-known Furstenberg correspondence principle between ergodic theory and combinatorics (also discussed previously). […]
3 June, 2011 at 7:55 pm
The Furstenberg multiple recurrence theorem and finite extensions « What’s new
[…] As is well known, the Furstenberg multiple recurrence theorem is equivalent to Szemerédi’s theorem, thanks to the Furstenberg correspondence principle; see for instance these lecture notes of mine. […]
26 November, 2011 at 12:43 pm
P (@mathe_magician)
I just encountered this post and I was wondering how restrictive is your shift invariance assumption?If i’m correct, a measure preserving system is always shift invariant by your definition.
Does lemma 1 hold if the shift invariance assumption is dropped?
26 November, 2011 at 1:14 pm
Terence Tao
Very little can be said if there is no shift-invariance (or something resembling shift-invariance) assumed. For instance, consider the circle shift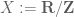 ,
,  for some real
for some real  , let
, let  be the (highly non-invariant) Dirac mass at 0, and let
be the (highly non-invariant) Dirac mass at 0, and let 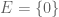 . Then Lemma 1 completely fails. (Of course, this is not anywhere close to a measure-preserving system.)
. Then Lemma 1 completely fails. (Of course, this is not anywhere close to a measure-preserving system.)
27 March, 2013 at 7:33 pm
An informal version of the Furstenberg correspondence principle | What's new
[…] to the string , and leads to the Furstenberg correspondence principle, discussed for instance in these previous blog posts. Such principles allow one to rigorously pass back and forth between the […]
20 July, 2015 at 8:22 pm
A nonstandard analysis proof of Szemeredi’s theorem | What's new
[…] to an averaging argument of Varnavides; see for instance Chapter 11 of my book with Van Vu or this previous blog post for a discussion. We have removed the cases as they are trivial and somewhat […]
5 March, 2017 at 10:38 am
Furstenberg limits of the Liouville function | What's new
[…] a function on the natural numbers taking values in , one can invoke the Furstenberg correspondence principle to locate a measure preserving system – a probability space together with a […]
13 April, 2017 at 2:27 pm
254A, Lecture 15: The Furstenberg-Zimmer structure theorem and the Furstenberg recurrence theorem | What's new
[…] are needed for other recurrence results involving IP systems or Hales-Jewett type results; see Lecture 10 for more […]
27 November, 2020 at 9:51 pm
Marcel K. Goh
Hi Prof. Tao, I am wondering exactly how averaging (2”) over all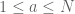 gives (2). I tried interchanging the sums but I’m not sure how that removes the
gives (2). I tried interchanging the sums but I’m not sure how that removes the  from the exponents of T. Is the
from the exponents of T. Is the 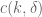 in (2), (2′), and (2”) the same constant?
in (2), (2′), and (2”) the same constant?
28 November, 2020 at 12:30 pm
Terence Tao
The various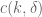 are not the same (the bound obtained in (2) will be about
are not the same (the bound obtained in (2) will be about  times smaller than the one in (2”)). Actually one should average (2”) over those
times smaller than the one in (2”)). Actually one should average (2”) over those 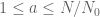 ; the point being that every
; the point being that every  has at most
has at most  representations of the form
representations of the form  with
with 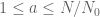 and
and  .
.
28 November, 2020 at 1:52 pm
Marcel K. Goh
Thanks, Prof. Tao! That cleared it up for me.
10 February, 2024 at 10:52 pm
Anonymous
Hi Prof. Tao.
It appears that the link for your unpublished note your refer to in Remark 4 is dead.
[Link updated – T.]
11 February, 2024 at 1:16 am
T Retsu
He has converted the note to pdf:
https://www.math.ucla.edu/~tao/preprints/Expository/limiting.pdf