I’ve just uploaded to the arXiv the short note “A remark on primality testing and the binary expansion“, submitted to the Journal of the Australian Mathematical Society. In this note I establish the following result: for any sufficiently large integer n, there exists an n-bit prime p, such that the numbers for
are all composite. In particular, if one flips any one of the bits in the binary expansion of the prime p, one obtains a composite number. As a consequence, one obtains the (rather plausible) consequence that in order to (deterministically) test whether an n-bit integer is prime or not, one needs (in the worst-case) to read all n bits of the prime. (This question was posed to me by my colleague here at UCLA, Yiannis Moschovakis.)
Primes p of the form mentioned in the above result are somewhat rare at first; the first some prime is . But in fact, the argument in my note shows that the set of such primes actually has positive relative density inside the set of all primes. (Amusingly, this means that one can apply a theorem of Ben Green and myself and conclude that there are arbitrarily long arithmetic progressions of such primes, although I doubt that there is any particular significance or application to this conclusion.)
The same remark applies to other bases; thus, for instance, there exist infinitely many prime numbers with the property that if one changes any one of the base 10 digits of that number, one obtains a composite number. (Presumably the first such number can be located by computer search, though I did not attempt to do so.) [Update, Feb 25: see comments.]
Heuristically, a random n-bit integer has roughly a 1/n chance (up to multiplicative constants such as ) of being prime. So amongst the 2n numbers
for
and a fixed prime p, one expects about O(1) of these numbers to be prime on the average. A more refined calculation (using the Hardy-Littlewood prime tuples conjecture) suggests that the expected number of primes exceeds 1 (in fact it should be asymptotically
, where
is the twin prime constant), which means that the main result is unlikely to be established purely by the first moment method. Fortunately, a little bit of elementary sieving using, of all things, the prime factors of Mersenne numbers, allows one to manipulate the expected number of primes to be significantly less than 1, to the point where standard upper bound sieves (in particular, the Selberg sieve) give satisfactory results.
It is nice for a change to write an elementary paper of six eight pages in length; the only moderately advanced tools I use here are the prime number theorem in arithmetic progressions, and the standard upper bound from the Selberg sieve for any two-dimensional sieving problem (in which one is allowed to eliminate up to two residue classes mod q for every prime q).
[Update, Feb 25: It has been pointed out to me that the base 2 result was implicitly obtained by Cohen and Selfridge, and explicitly pointed out by Sun, using the covering congruence method of Erdős, so I have rewritten the paper to focus primarily on the case of general bases (to which it is not entirely clear that a set of covering congruences exists). The earlier version (which focused only on the base 2 case, and so is slightly simpler) can be found here.]
[Update, Feb 26: It should now also be possible to prove the following generalisation: for any base a and any r, there should exist infinitely many primes which become composite whenever one changes one of the digits, and also appends or deletes up to r of digits on either end of the digit expansion. My method comes very close to establishing this result, except for one annoying issue arising from the fact that numbers such as (with j, l = O(1)) can occasionally have a huge number of prime factors. This seems to be a rare event, though, so presumably one should be able to modify the argument to obtain this result. I’ll leave this for someone else to try, though. One should also be similarly able to replace “change one of the digits” to “delete or insert a digit at an arbitrary location”.]

21 comments
Comments feed for this article
25 February, 2008 at 1:19 pm
Ben
There’s a typo on the bottom of page 3: “wheneverf i if of this form” should be changed to “whenever i is of this form”.
25 February, 2008 at 2:18 pm
Thomas
Dear Terry, that’s very insteresting. I think these primes (at least in base 2) are called “sigularly dead end primes”, see sequence A065092 on OEIS.
25 February, 2008 at 5:46 pm
Anonymous
294001, I think.
25 February, 2008 at 6:32 pm
Terence Tao
Thanks for the comments (and for the solution to the little puzzle)!
25 February, 2008 at 8:47 pm
Jens Kruse Andersen
The base-10 case is called a weakly prime. The first are in http://www.research.att.com/~njas/sequences/A050249. I found the 1000-digit example (17*10^1000-17)/99+21686652 for http://www.primepuzzles.net/puzzles/puzz_017.htm.
25 February, 2008 at 11:31 pm
Tony
Sequence A065092 does not exactly meet your requirements because if prime p is an n-bit number then A065092 also requires that the (n+1)-bit number p+2^n is composite. Hence, the correct sequence, which is not in OEIS yet, has additional terms. That sequence begins 127, 173, 191, 223, 233, 239, 251, 257, 277, 337,…
26 February, 2008 at 11:39 am
Emmanuel Kowalski
Concerning the result of Heath-Brown and Puchta you mention in the paper (about even integers large enough being sum of two primes and at most 13 powers of 2, which is a rather remarkable approximation to Goldbach’s conjecture, first considered by Linnik if I remember right), Pintz and Ruzsa have announced that 13 can be replaced by 8, but the paper is not yet published (this is mentioned e.g. in “On the sum of two primes and k powers of two”, by Languasco, Pintz and Zaccagnini, Bull. London Math. Soc. 39 (2007) 771–780).
Either result is really impressive…
26 February, 2008 at 2:47 pm
Terence Tao
Dear all: Thanks for the references!
26 February, 2008 at 3:35 pm
harrison
Re the February 26 update: For fixed a, r, are there infinitely many primes that become composite when any r digits in their base-a expansion are changed? I can’t see an obvious heuristics in either direction (although I admittedly haven’t worked through the arithmetic of the PNT on this one.) Does anyone know an obvious counterexample?
26 February, 2008 at 4:41 pm
Terence Tao
Dear Harrison,
I suspect the answer is negative when a is large and r is at least 2, though actually proving this is probably hopeless with current technology. The prime number theorem asserts, roughly speaking, that an n-digit number has a probability about 1/n of being prime (suppressing constants). On the other hand, the number of ways one can modify r digits of an n-digit number (with r fixed and n going to infinity) is comparable to n^r. Non-rigorous heuristics then suggest that the probability that any given number will remain composite after _all_ possible r-digit modifications is about (1-1/n)^{n^r} ~ exp( – n^{r-1} ). On the other hand, the number of n-digit numbers is about exp(n). This suggests (but does not prove) that for sufficiently large n, there are only finitely many numbers with this property for r > 2.
On the other hand, one can try to use covering congruences to make an end run around this problem; by considering what happens in small moduli (mod 2, mod 3, etc.) one can already eliminate a significant fraction of all r-digit modifications from being prime by choosing the initial prime to lie in a well-chosen residue class. It may be that by pushing this enough one can get some positive result for small a and r. For instance, it was recently established by Yuan (Acta Arith. 2004) that there are infinitely many numbers which become composite after subtracting any two powers of two.
26 February, 2008 at 7:37 pm
anonymous
A tiny note: if the goal is to show that you have to examine every digit to prove primality, then this is immediate in bases larger than 2. For instance in base 10 you can change any digit to make the sum of the digits of the number divisible by 9, which would make it composite. I realize this is different from *any* change of digit making it composite, which is what you’re after…
29 February, 2008 at 12:22 am
Jonathan Vos Post
This is also related to:
http://www.research.att.com/~njas/sequences/A133219
A133219 Smallest composite integer in base n which remains composite after altering any one or two digits.
n a(n)
2 1010100
3 2200100
4 20130000
5 3243003420
6 55111253530
7 5411665056000
8 33254100107730
9 210324811482600
10 977731833235239280
OFFSET
2,1
COMMENT
Changing the most significant digit to 0 is allowed. The problem (base 10) was posed by W. Sierpinski, published in 1977. There are an infinite number of solutions if a certain Erdos conjecture on congruences is true. a(2) through a(9) are proved minimal, a(10) has not yet been proved minimal.
LINKS
Witold Jarnicki and Maciej Zenczykowski, On a property of the number 977731833235239280.
EXAMPLE
a(3) base 10 = 1953.
a(4) base 10 = 34560.
a(5) base 10 = 7000485.
a(6) base 10 = 354748446.
a(7) base 10 = 77478704205.
a(8) base 10 = 1878528135128.
a(9) base 10 = 48398467146642.
KEYWORD
base,more,nonn
AUTHOR
Jonathan Vos Post (jvospost2(AT)yahoo.com), Oct 11 2007 [not the preferred email address anymore]
EXTENSIONS
a(2) and the definition were corrected by Witold Jarnicki, Oct 11 2007
31 March, 2008 at 11:45 am
Dave
Fermat’s (Little) Theorem: If p is a prime and if a is any integer, then ap = a (mod p). In particular, if p does not divide a, then ap-1 = 1 (mod p).
I think it would be interesting to use base 3 a ternary code in investigating primes. More specifically I would explore pseudoprimes. Further I would explore Mersenne numbers and Stern primes as they are unusual subsets within primality. I wouldn’t consider your paper so elementry as you may think. I would choose pseudoprimes first and see what develops.
If you can envision all primes as a tapestry, I would consider unusual subsets of primes as focal points within the tapestry.
14 May, 2008 at 12:35 am
Jaime Montuerto
dear Dr Tao,
I am working on a binary factoring algorithm and discovered this interesting property of 3 bit binary polynomials, 2^x + 2^y + 2^z , if x,y,z are all even, then the sum of these binary terms is multiple of 3. Is there a known theorem about this?
Jaime Montuerto
Sydney Australia
16 May, 2008 at 11:01 am
Terence Tao
Dear Jaime,
If x,y,z are all even, then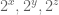 are all powers of 4. Since 4 = 1 mod 3,
are all powers of 4. Since 4 = 1 mod 3, 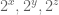 will also be equal to 1 mod 3, which is why
will also be equal to 1 mod 3, which is why  is a multiple of 3.
is a multiple of 3.
21 May, 2008 at 9:28 pm
Jaime Montuerto
Dear Terry,
Thank you very much for your response. It is also true that 2^x+2^y+2^z, if all x,y,z are all odd it’s also multiple of 3. The problem of a prime in binary form
and if one of the bit is flip off (remove) the result would have a 1/2 chance of being multiple of 3. And if not multiple of 3 then the remainder would flip from 1 to 2 and vice versa.
This problem has the same algorithmic difficulty with even goldbach conjecture, ‘all even number is sum of 2 prime numbers’. I have an algorithm that gets pairs of primes for this. The basic component is exactly analysing what bit/s to transfer to another factor and what to add.
These are the result of my works.
1. Two even power bits equals to one odd power bit. 2^x+2^y = 2^z
ie, x,y are even and z is odd.
2. Two odd power bits equals to one even power bit. The opposite of above.
3. One even bit and one odd bit is a multiple of 3. Hence fermat numbers with one odd power bit is always multiple of 3, 1 being considered to have even power bit.
3. So that a set of 3 odd or even bits is multiple of 3.
Hence in analyzing the multiplicity by 3 of all binary integers just group all even power and odd power bits into set of 3 or simply the remainder of 3 to the sum, the remaining odd and even just paired them up. The result would have either no bit remains, one odd bit or one even bit. That’s why removing or adding a bit to any prime number would result in a 1/2 chance of being multiple of 3.
I am not quite sure whether these are quite obvious the way you show the
first one.
truly appreciated,
jaime
23 May, 2008 at 9:46 am
Terence Tao
Dear Jaime,
Divisibility with regard to small moduli (2, 3, etc.) are best approached using modular arithmetic; note from Cauchy’s theorem (or Euler’s theorem) that 2^x mod p is periodic in x with period p-1, which is why one has a lot of regularity when looking at small moduli.
But the bulk of the difficulty in primality testing is not with the small moduli, but with the large moduli. Consider for instance two numbers n and m. n is a 500-bit prime, whereas m is the product of two 250-bit primes. Both of these numbers are not divisible by 2, 3, 5, 7, or indeed by any prime with 249 bits or less. Nevertheless, only one of them is prime. How does one distinguish between the two just from the binary expansion? Applying divisibility tests all the way up to the 250 bit level is impractical. There are of course other methods for primality testing (for instance, Cauchy’s theorem as mentioned above already filters out most (though not all) non-primes), but they do require a certain amount of number theory beyond the modular arithmetic of small moduli.
23 May, 2008 at 10:50 pm
Jaime Montuerto
Dear Terry,
Again thanks for your considerable response.
Extending my argument I only mentioned prime 3 because it has those interesting properties. But there is a misinterpretation in my analysis in terms of the probability of being multiple of 3 if any bit is removed. It’s not 1/2 chance but 1/4 chance of being multiple of 3.
Here a more elaborated analysis.
Any prime larger than 3 has either 1 or 2 remainder mod 3. This is the same as saying a 1/2 chance of either 1 or 2. In my algorithm, any bit has the same remainder mod 3. Therefore if a particular prime in question say has 1 remainder and removing any bit has same 1/2 probability of being 1. So the actual probability is 1/2 * 1/2.
The probability with prime 5 is 1/4 * 1/4. The first probability is that any prime chosen would have a 1/4 chance of remainder in one of {1,2,3,4} and the second probability factor is that a bit removed would have same probability of being the same remainder.
This is the same for 7 of 1/6*1/6, 11 of 1/10*1/10, 13 of 1/12*1/12 and so on till the largest prime but less than the actual prime in question. Then i noticed that all these probabilities are the actual euler totient function square of the small primes.
So the probability of a smaller prime being the factor of a composite result would be its 1/phi(small prime) * 1/phi(small prime). As a whole, the overall probability is the summations of these probabilities. Hence, 1/2*1/2 + 1/4*1/4 + 1/6*1/6 + … + 1/square of totient function of largest prime.
This summation is uncannily similar to the riemann zeta function summation. For the term 1/n^2 in the riemann zeta function, what is the semiotic meaning of n in relation to euler totient term function (1 – 1/p)? Somehow it seems to me that the relationship of n to p is its totient function. So that the euler expression factor of (1-1/p) on the right hand side of equation is the probability of that prime p whereas the equivalent term of probability in the riemann zeta function is 1/n^2 which is to say that 1/square of the totient function of p. The 1/n^2 is the probability that relates to (1-1/p) as one to one mapping.
This is just an observation. And I hope I am clear in what I have said.
I would be happy for any reaction you could give.
Thanks again for your response – it was much appreciated.
Jaime
3 July, 2008 at 5:19 am
liuxiaochuan
Dear Professor 陶:
Xian-Jin Li uploaded a paper giving a proof of the Riemann hypothesis.
http://arxiv.org/abs/0807.0090
I wonder if you are paying attention to this.
刘
1 August, 2010 at 12:02 am
Charles Johnson
A proof of the Riemann hypothesis
Authors: Xian-Jin Li
(Submitted on 1 Jul 2008 (v1), last revised 6 Jul 2008 (this version, v4))
Abstract: This paper has been withdrawn by the author, due to a mistake on page 29.
5 April, 2013 at 2:56 pm
Warren D.Smith
1. typo: the “prime” 231 should have been 331 on the first page of your paper.
2. your paper’s main result theorem 1.2 can be strengthened so that the 1<=i is replaced by 0<=i. To do so, employ Brun's theorem (stated as "corollary A3" on Tao paper's last page)
to see that the proportion of the weaker theorem's
primes N which disobey this strengthened theorem, is
asymptotically zero.
3. Define P to be an "every bit matters" prime if altering any single bit in its binary representation, destroys primality. I conjecture that a constant fraction B of all primes, are every bit matters primes.
I conjecture that B=exp(-2*C2/ln2) where
C2=0.660161815846869573927812110014
is the Hardy-Littlewood twin prime constant.
Thus B=0.14884878474999065378100135978.
Similar notions can be defined for radices other than 2.
Then similar exact conjectures can be made.
One can prove a positive lower bound on liminfB, but sadly I
have no proof that liminfB=limsupB<1.
4. To prove limsupB<1 one would want (at least) to prove there exist
an infinity of primes such that when you alter one bit, you still have a prime.
I can prove that there exist an infinite set of primes, such that
altering 2 bits in their binary form, still gives a prime.
Indeed, this is even true if the two bits are demanded to lie in
the $n^{0.51}$ last bits of that prime (for n-bit-long primes written
in binary, all large-enough n).