In Lecture 11, we studied compact measure-preserving systems – those systems in which every function
was almost periodic, which meant that their orbit
was precompact in the
topology. Among other things, we were able to easily establish the Furstenberg recurrence theorem (Theorem 1 from Lecture 11) for such systems.
In this lecture, we generalise these results to a “relative” or “conditional” setting, in which we study systems which are compact relative to some factor of
. Such systems are to compact systems as isometric extensions are to isometric systems in topological dynamics. The main result we establish here is that the Furstenberg recurrence theorem holds for such compact extensions whenever the theorem holds for the base. The proof is essentially the same as in the compact case; the main new trick is to not to work in the Hilbert spaces
over the complex numbers, but rather in the Hilbert module
over the (commutative) von Neumann algebra
. (Modules are to rings as vector spaces are to fields.) Because of the compact nature of the extension, it turns out that results from topological dynamics (and in particular, van der Waerden’s theorem) can be exploited to good effect in this argument.
[Note: this operator-algebraic approach is not the only way to understand these extensions; one can also proceed by disintegrating into fibre measures
for almost every
and working fibre by fibre. We will discuss the connection between the two approaches below.]
— Hilbert modules —
Let be a measure-preserving system, and let
be a factor map, i.e. a morphism from X to another system
. The algebra
can be viewed (using
) as a subalgebra of
; indeed, it is isomorphic to
, where
is the pullback of
by
.
Example 1. Throughout these notes we shall use the skew shift as our running example. Thus, in this example, with shift
for some fixed
(which can be either rational or irrational),
with shift
, with factor map
. In this case,
can be thought of (modulo equivalence on null sets, of course) as the space of bounded functions on
which depend only on the first variable.
Example 2. Another (rather trivial) example is when the factor system Y is simply a point. In this case, is the space of constants and can be identified with
. At the opposite extreme, another example is when Y is equal to X. It is instructive to see how all of the concepts behave in each of these two extreme cases, as well as the typical intermediate case presented in Example 1.
The idea here will be to try to “relativise” the machinery of Hilbert spaces over to that of Hilbert modules over
. Roughly speaking, all concepts which used to be complex or real-valued (e.g. inner products, norms, coefficients, etc.) will now take values in the algebra
. The following table depicts the various concepts that will be relativised:
| Absolute / unconditional | Relative / conditional |
| Constants |
Factor-measurable functions |
| Expectation |
Conditional expectation |
| Inner product |
Conditional inner product |
| Hilbert space |
Hilbert module |
| Finite-dimensional subspace |
Finitely generated module |
| Almost periodic function | Conditionally almost periodic function |
| Compact system | Compact extension |
| Hilbert-Schmidt operator | Conditionally Hilbert-Schmidt operator |
| Weakly mixing function | Conditionally weakly mixing function |
| Weakly mixing system | Weakly mixing extension |
(The last few notions in this table will be covered in the next lecture, rather than this one.)
Remark 1. In information-theoretic terms, one can view Y as representing all the observables in the system X that have already been “measured” in some sense, so that it is now permissible to allow one’s “constants” to depend on that data, and only study the remaining information present in X conditioning on the observed values in Y. Note though that once we activate the shift map T, the data in Y will similarly shift (by S), and so the various fibres of can interact with each other in a non-trivial manner, so one should take some caution in applying information-theoretic intuition to this setting.
We have already seen that the factor Y induces a sub--algebra
of
. We therefore have a conditional expectation map
defined for all absolutely integrable f by the formula
. (1)
In general, this expectation only lies in , though for the functions we shall eventually study, the expectation will always lie in
when needed.
As stated in the table, conditional expectation will play the role in the conditional setting that the unconditional expectation plays in the unconditional setting. Note though that the conditional expectation takes values in the algebra
rather than in the complex numbers. We recall that conditional expectation is linear over this algebra, thus
(2)
for all absolutely integrable f, g and all .
Example 3. Continuing Example 1, we see that for any absolutely integrable f on , we have
almost everywhere.
Let be the space of all
such that the conditional norm
(3)
lies in (rather than merely in
, which it does automatically). Thus for instance we have the inclusions
. (4)
The space is easily seen to be a vector space over
, and moreover (thanks to (2)) is a module over
.
Exercise 1. If we introduce the inner product
(5)
(which, initially, is only in ), establish the pointwise Cauchy-Schwarz inequality
(6)
Example 4. Continuing Examples 1 and 3, consists (modulo null set equivalence) of all measurable functions
such that
is bounded a.e. in y, with the relative inner product
(7)
defined a.e. in y. Observe in this case that the relative Cauchy-Schwarz inequality (6) follows easily from the standard Cauchy-Schwarz inequality.
Exercise 2. Show that the function is a norm on
, which turns that space into a Banach space. (Hint: you may need to “relativise” one of the standard proofs that
is complete. You may also want to start with the skew shift example to build some intuition.) Because of this completeness, we refer to
as a Hilbert module over
.
As is a morphism, one can easily check the intertwining relationship
(7)
for all and integers n. As a consequence we see that the map T (and all of its powers) preserves the space
, and furthermore is conditionally unitary in the sense that
(8)
for all and integers n.
In the Hilbert space one can create finite dimensional subspaces
for any
. Inside such subspaces we can create the bounded finite-dimensional zonotopes
. Observe (from the Heine-Borel theorem) that a subset E of
is precompact if and only if it can be approximated by finite-dimensional zonotopes in the sense that for every
, there exists a finite-dimensional zonotope Z of
such that E lies within the
neighbourhood of Z.
Remark 2. There is nothing special about zonotopes here; just about any family of bounded finite-dimensional objects would suffice for this purpose. In fact, it seems to be slightly better (for the purposes of quantitative analysis, and in particular in controlling the dependence on dimension d) to work instead with octahedra, in which the constraint is replaced by
; see this paper of mine in which this perspective is used.
Inspired by this, let us make some definitions. A finitely generated module of is any submodule of
of the form
, where
. Inside such a module we can define a finitely generated module zonotope
.
Definition 1. A subset E of
is said to be conditionally precompact if for every
, there exists a finitely generated module zonotope Z of
such that E lies within the
-neighbourhood of Z (using the norm from Exercise 2).
A function
is said to be conditionally almost periodic if its orbit
is conditionally precompact.
A function
is said to be conditionally almost periodic in measure if every
there exists a set E in Y of measure at most
such that
is conditionally almost periodic.
The system X is said to be a compact extension of Y if every function in
is conditionally almost periodic in measure.
Example 5. Any bounded subset of is conditionally precompact (though note that it need not be precompact in the topological sense, using the topology from Exercise 2). In particular, every function in
is conditionally almost periodic.
Example 6. Every system is a compact extension of itself. A system is a compact extension of a point if and only if it is a compact system.
Example 7. Consider the skew shift (Examples 1, 3, 4), and consider the orbit of the function . A computation shows that
(9)
which reveals (for irrational) that f is not almost periodic in the unconditional sense. However, observe that all the shifts
lie in the zonotope
generated by a single generator f, and so f is conditionally almost periodic.
Exercise 3. Consider the skew shift (Examples 1,3,4,7). Show that a sequence is conditionally precompact if and only if the sequences
are precompact in
(with the usual Lebesgue measure) for almost every y.
Exercise 4. Show that the space of conditionally almost periodic functions in is a shift-invariant
module, i.e. it is closed under addition, under multiplication by elements of
, and under powers
of the shift operator.
Exercise 5. Consider the skew shift (Examples 1,3,4,7 and Exercise 3) with irrational, and let
be the function defined by setting
whenever
and
. Show that f is conditionally almost periodic in measure, but not conditionally almost periodic. Thus the two notions can be distinct even for bounded functions (a subtlety that does not arise in the unconditional setting).
Exercise 6. Let denote the collection of all measurable sets E in X such that
is conditionally almost periodic in measure. Show that
is a shift-invariant sub-
-algebra of
that contains
, and that a function
is conditionally almost periodic in measure if and only if it is
-measurable. (In particular,
is the maximal compact extension of Y.) [Hint: you may need to truncate the generators
of various module zonotopes to be in
rather than
.]
Exercise 7. Show that the skew shift (Examples 1, 3, 4, 7 and Exercises 3,5) is a compact extension of the circle shift. (Hint: Use Example 7 and Exercise 6. Alternatively, approximate a function on the skew torus by its vertical Fourier expansions. For each fixed horizontal coordinate y, the partial sums of these vertical Fourier series converge (in the vertical sense) to the original function, pointwise in y. Now apply Egorov’s theorem.)
Exercise 8. Show that each of the iterated skew shifts (Exercise 8 from Lecture 9) are compact extensions of the preceding skew shift.
Exercise 9. Let be a measure-preserving system, let G be a compact metrisable group with a closed subgroup H, let
be measurable, and let
be the extension of Y with underlying space
, with measure equal to the product of
and Haar measure, and shift map
. Show that
is a compact extension of Y.
— Multiple recurrence for compact extensions —
Let us say that a measure-preserving system obeys the uniform multiple recurrence (UMR) property if the conclusion of the Furstenberg multiple recurrence theorem holds for this system, thus for all
and all non-negative
with
, we have
. (10)
Thus in Lecture 11 we showed that all compact systems obey UMR, and in Lecture 12 we showed that all weakly mixing systems obey UMR. The Furstenberg multiple recurrence theorem asserts, of course, that all measure-preserving systems obey UMR.
We now establish an important further step (and, in many ways, the key step) towards proving that theorem:
Theorem 1. Suppose that
is a compact extension of
. If Y obeys UMR, then so does X.
Note that the converse implication is trivial: if a system obeys UMR, then all of its factors automatically do also.
Proof of Theorem 1. Fix , and fix a non-negative function
with
. Our objective is to show that (10) holds. As X is a compact extension, f is conditionally almost periodic in measure; by definition (and uniform integrability), this implies that f can be bounded from below by another conditionally almost periodic function which is non-negative with positive mean. Thus we may assume without loss of generality that f is conditionally almost periodic.
We may normalise and
for some
. The reader may wish to follow this proof using the skew shift example as a guiding model.
Let be a small number (depending on k and
) to be chosen later. If we set
, then E must have measure at least
.
Since f is almost periodic, we can find a finitely generated module zonotope whose
-neighbourhood contains the orbit of f. In other words, we have an identity of the form
(11)
for all n, where with norm at most 1, and
is an error with
almost everywhere.
By splitting into real and imaginary parts (and doubling d if necessary) we may assume that the are real-valued. By further duplication we can also assume that
for each i. By rounding off
to the nearest multiple of
for each y (and absorbing the error into the
term) we may assume that
is always a multiple of
. Thus each
only takes on
values.
Let K be a large integer (depending on k, d, ,
) to be chosen later. Since the factor space Y obeys UMR, and E has positive measure in Y, we know that
(12)
In other words, there exists a constant such that
(13)
for a set of n of positive lower density, where is the set
. (14)
Let n be as above. By definition of and
(and (8)), we see that
(15)
for all and
. Meanwhile, from (11) we have
(16)
for all and
.
Fix y. For each , the d-tuple
ranges over a set of cardinality
. One can view this as a colouring of
into
colours. Applying van der Waerden’s theorem (Exercise 3 from Lecture 4), we can thus find (if K is sufficiently large depending on
) an arithmetic progression
in
for each y such that
. (17)
The quantities a(y) and r(y) can of course be chosen to be measurable in y. By the pigeonhole principle, we can thus find a subset of
of measure at least
for some
depending on c, K, d,
but independent of n, and an arithmetic progression
in
such that
(18)
for all . (The quantities a and r can still depend on n, but this will not be of concern to us.)
Fix these values of a, r. From (16), (18) and the triangle inequality we see that
(19)
for all and
. Recalling that f was normalised to have
norm 1, it is then not hard to conclude (by induction on k and the relative Cauchy-Schwarz inequality) that
(20)
and thus (by another application of relative Cauchy-Schwarz)
. (21)
But from (15) we have
(22)
and so by several more applications of relative Cauchy-Schwarz we have
(23)
for some positive quantity . From (21), (23) we conclude that
(24)
for , if
is small enough. Integrating this in y and using the shift-invariance we conclude that
. (25)
The quantity r depends on n, but ranges between 1 and K-1, and so (by the non-negativity of f)
(26)
for a set of n of positive lower density. Averaging this for n from 1 to N (say) one obtains (10) as desired.
Thus for instance we have now established UMR for the skew shift as well as higher iterates of that shift, thanks to Exercises 7 and 8.
Remark 3. One can avoid the use of Hilbert modules, etc. by instead appealing to the theory of disintegration of measures (Theorem 4 from Lecture 9). We sketch the details as follows. First, one has to restrict attention to those spaces X which are regular, though an inspection of the Furstenberg correspondence principle (Lecture 10) shows that this is in fact automatic for the purposes of such tasks as proving Szemerédi’s theorem. Once one disintegrates with respect to
, the situation now resembles the concrete example of the skew shift, with the fibre measures
playing the role of integration along vertical fibers
. It is then not difficult (and somewhat instructive) to convert the above proof to one using norms such as
rather than the module norm
. We leave the details to the reader (who can also get them from Furstenberg’s book).
Remark 4. It is an intriguing question as to whether there is any interesting non-commutative extension of the above theory, in which the underlying von Neumann algebra is replaced by a non-commutative von Neumann algebra. While some of the theory seems to extend relatively easily, there does appear to be some genuine difficulties with other parts of the theory, particularly those involving multiple products such as
.
Remark 5. Just as ergodic compact systems can be described as group rotation systems (Kronecker systems), it turns out that ergodic compact extensions can be described as (inverse limits of) group quotient extensions, somewhat analogously to Lemma 2 from Lecture 6. Roughly speaking, the idea is to first use some spectral theory to approximate conditionally almost periodic functions by conditionally quasiperiodic functions – those functions whose orbit lies on a finitely generated module zonotope (as opposed to merely being close to one). One can then use the generators of that zonotope as a basis from which to build the group quotient extension, and then use some further trickery to make the group consistent across all fibres. The precise machinery for this is known as Mackey theory; it is of particular importance in the deeper structural theory of dynamical systems, but we will not describe it in detail here, instead referring the reader to the papers of Furstenberg and of Zimmer.
[Update, Mar 5: Exercise added.]
[Update, Mar 12: Definition of conditionally almost periodic measure tweaked (to an equivalent definition) in order to simplify the proof of Theorem 1.]

31 comments
Comments feed for this article
2 March, 2008 at 9:24 pm
254A, Lecture 14: Weakly mixing extensions « What’s new
[…] Hilbert-Schmidt operators, randomness, weak mixing Having studied compact extensions in the previous lecture, we now consider the opposite type of extension, namely that of a weakly mixing extension. Just as […]
6 March, 2008 at 11:21 am
Anonymous
All the formulas in this post seem to lack backlashases before TeX commands.
6 March, 2008 at 1:28 pm
John Armstrong
Anonymous, this is a problem on WordPress’ end, as I noted earlier today, or possibly all the way back to the new version of PHP, which Blake Stacey noticed recently.
28 December, 2008 at 12:16 am
liuxiaochuan
Dear Professor Tao:
I got several small corrections and a question:
1, In Example 1, the shift should be
2, In (3), the right hand side should be
3,in Exercise 3, the tex cod “\cdot”, with “\”missing.
and
I don’t know how to compute (9).
28 December, 2008 at 9:41 am
Terence Tao
Thanks for the corrections! There were some typos in (9); one can work things out by first computing what is by induction (it is
is by induction (it is  ).
).
8 January, 2009 at 9:14 am
254A, Lecture 15: The Furstenberg-Zimmer structure theorem and the Furstenberg recurrence theorem « What’s new
[…] for a point, and we have already shown that UMR is preserved by compact extensions (Theorem 1 of Lecture 13) and by weakly mixing extensions (Theorem 1 of Lecture 14). The former result lets us climb the […]
24 October, 2009 at 11:35 am
Ergodic Ramsey Theory (by Yuri Lima) « Disquisitiones Mathematicae
[…] Compact and weak-mixing […]
16 June, 2010 at 2:01 pm
Alex
Dear Professor Tao,
About Remark 4, do you have any reference in which this question have been studied?
thanks,
Alex
16 June, 2010 at 3:12 pm
Terence Tao
I recently wrote a paper with Tim Austin and Tanja Eisner on this topic at
There is also previous work by Niculescu-Stroh-Zsido, Duvenhage, and Beyers-Duvenhage-Stroh, among others. Roughly speaking, it seems that triple averages are still more or less OK if one makes reasonable assumptions (such as ergodicity), but higher order averages can behave quite badly unless one makes very strong assumptions (e.g. asymptotic abelianness).
1 May, 2011 at 3:34 pm
ERT16: Compact extensions « Disquisitiones Mathematicae
[…] This post of Terence Tao has much in common with our discussion. […]
3 June, 2011 at 7:55 pm
The Furstenberg multiple recurrence theorem and finite extensions « What’s new
[…] that the multiple recurrence property is preserved under compact extensions; see for instance these lecture notes, which is devoted entirely to this step. This step requires quite a bit of measure-theoretic and/or […]
22 October, 2011 at 12:35 pm
pavel zorin
Dear Prof. Tao,
could you please give some hints or references on how to approximate conditionally almost periodic functions by conditionally quasiperiodic functions?
For me this would be the last step in understanding why the factor in Exercise 6 coincides with that defined by Furstenberg in his ’77 paper.
best regards,
pavel
22 October, 2011 at 1:27 pm
Terence Tao
I’m not sure how you are defining conditionally quasiperiodic functions in general, but in the case of compact extensions, it is possible to represent such extensions (under some mild topological assumptions on the underlying space) as extensions by compact abelian groups, at which point one can use Fourier analysis in that group to approximate arbitrary functions in the extension by functions which are “conditionally quasiperiodic” in the sense that they are finite linear combinations of functions that are eigenfunctions of the group action (or equivalently, are scalar multiples of characters in almost every fibre).
Furstenberg’s book contains a number of equivalent characterisations of compact extensions, and on the relationship between a number of slightly different versions of relative almost periodicity.
26 October, 2011 at 10:55 am
Anonymous
I used the definition from Remark 5. The problem was that the construction of the representation as a group extension say by Furstenberg assumes that the extension is spanned by generalized eigenfunctions.
I have now adapted the argument from Lemma 2.14.17 in your book (using conditional Hilbert-Schmidt operators) to show that the generalized eigenfunctions are dense in conditionally almost periodic functions.
By the way, in the book (Proposition 2.14.11) you take a weak limit of operators on L²(X|Y). In that particular case a limit can be constructed explicitly using the mean ergodic theorem on as in Furstenberg’s book. Is there also an abstract proof of existence? (the problem being that L²(X|Y) is not a Hilbert space and fiberwise constructions are not straightforward because there may be uncountably many fibers).
as in Furstenberg’s book. Is there also an abstract proof of existence? (the problem being that L²(X|Y) is not a Hilbert space and fiberwise constructions are not straightforward because there may be uncountably many fibers).
26 October, 2011 at 11:35 am
Terence Tao
Ah, I see where you are coming from now. Yes, by taking a bunch of “conditional eigenspaces” of a conditional Hilbert-Schmidt operator, one can achieve the desired approximatino.
With regards to the weak limit, I guess one needs to use the weak topology of L^2(X) rather than L^2(X|Y) to get weak compactness. Note that the operators S_N involved are uniformly bounded in L^2(X). I’ll make a note of that in the errata.
5 December, 2012 at 8:29 pm
Joel Moreira
Dear Prof. Tao
In the proof of Theorem 1, right after equation (17) you claim that a(y) and r(y) can be made measurable in y. Maybe I’m missing something obvious but I don’t understand why this is true, could you give some additional explanation?
5 December, 2012 at 9:02 pm
Terence Tao
Arrange the set of pairs in some well-ordered fashion (e.g. lexicographic) and then for each
in some well-ordered fashion (e.g. lexicographic) and then for each  , take
, take  to be the minimal
to be the minimal  that obeys the required property.
that obeys the required property.
5 December, 2012 at 9:13 pm
Joel Moreira
Well, I was having trouble figuring out why the set of y’s for which some fixed (a,r) works is measurable, but after taking some time to write down the definitions I figured it out. Thank you for the quick answer.
1 January, 2013 at 3:14 pm
cuttheknot
Dear Prof. Tao, how can I deduce inequality (23) from (22)?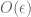 come from in (22)? (Shouldn’t it be identical to (15)?)
come from in (22)? (Shouldn’t it be identical to (15)?)
Also, where does the
1 January, 2013 at 6:10 pm
Terence Tao
Iterating relative Cauchy-Schwarz will give (23) from (22) when k is a power of two; the general case then follows since f is bounded by 1 (and every k is certainly bounded above by a power of two).
You’re right that (22) just follows from (15) without the epsilon loss; I’ll amend the text to reflect this.
2 January, 2013 at 3:44 am
cuttheknot
Ok, now I see. Thank you!
21 May, 2013 at 4:30 pm
Multiple recurrence and convergence results associated to $F_{p}^{omega}$-actions | What's new
[…] is the Haar probability measure on ; see this previous blog post. The equation defining corresponds to the constraint (4) mentioned earlier. Among other things, […]
20 July, 2015 at 8:23 pm
A nonstandard analysis proof of Szemeredi’s theorem | What's new
[…] This gives the structure of a (pre-)Hilbert module over , as discussed in this previous blog post. […]
22 December, 2016 at 6:57 am
Mike Schnurr
I’m still trying to grapple with the Hilbert module, so I have a question about conditional precompactness that might be pretty basic in light of a better understanding of the module.
First of all, am I correct in presuming that if then for all
then for all  I will assume I am correct on this for my main question
I will assume I am correct on this for my main question
Now, I’m working with a different formulation of conditional precompactness. Namely, is conditionally precompact if for all
is conditionally precompact if for all  there exists
there exists  such that
such that 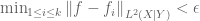 a.e. So if I have
a.e. So if I have  conditionally almost periodic with
conditionally almost periodic with  for a given
for a given  can my
can my 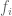 be chosen such that
be chosen such that  I would imagine it is possible, same as nearly all considerations with norms of functions. Still, I need to be sure, and I don't understand the Hilbert module well enough at this point to figure out how to grapple with answering it on my own.
I would imagine it is possible, same as nearly all considerations with norms of functions. Still, I need to be sure, and I don't understand the Hilbert module well enough at this point to figure out how to grapple with answering it on my own.
22 December, 2016 at 12:21 pm
Terence Tao
The answer to the first question is “Yes”, assuming of course that is measure preserving. I’m afraid I don’t understand the second question – how is the set
is measure preserving. I’m afraid I don’t understand the second question – how is the set  related to the function
related to the function  ?
?
22 December, 2016 at 1:46 pm
Mike Schnurr
Sorry for not making it clearer. Since is conditionally almost periodic, I mean for
is conditionally almost periodic, I mean for  to be exactly the set
to be exactly the set 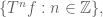 where yes,
where yes,  is measure preserving. Additionally (if relevant),
is measure preserving. Additionally (if relevant),  is an extension of some
is an extension of some  and I’m even assuming both are invertible
and I’m even assuming both are invertible
23 December, 2016 at 12:06 pm
Terence Tao
In which case you probably mean rather than
rather than  . One can certainly achieve this normalisation, though it is somewhat unnatural to do so: one can partition
. One can certainly achieve this normalisation, though it is somewhat unnatural to do so: one can partition  into small sets
into small sets 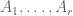 , and then replace each of the
, and then replace each of the 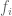 by functions
by functions 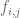 for
for  , where
, where 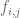 is defined to equal
is defined to equal 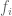 on
on 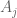 and is chosen more or less arbitrarily on the remaining portion of
and is chosen more or less arbitrarily on the remaining portion of  (or
(or  ) in order to achieve the required normalisation
) in order to achieve the required normalisation  .
.
25 August, 2020 at 7:41 am
Abhishek Khetan
Dear Prof. Tao,
I have a question regarding Exmaple 7.
We have . Fix
. Fix  and write
and write 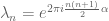 . Then
. Then  .
.
You have mentioned that is not (unconditionally) almost periodic if
is not (unconditionally) almost periodic if  is irrational. I am trying to see what changes when
is irrational. I am trying to see what changes when  is rational.
is rational.
To check for almost periodicity, we need to look at the quantity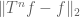 which by Fubini is equal to
which by Fubini is equal to  . By a change of variable this is same as
. By a change of variable this is same as  which does not depend on the choice of
which does not depend on the choice of  .
.
So my conclusion is that is not almost peiodic regardless of the choice of
is not almost peiodic regardless of the choice of  . Is this correct or have I made a mistake somwhere?
. Is this correct or have I made a mistake somwhere?
Also, there is a minor typo in Example 3. The expression should be replaced by
should be replaced by 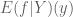 .
.
Thank you.
31 August, 2020 at 5:14 pm
Terence Tao
Thanks for the correction. It is true that even for rational the function here is not unconditionally almost periodic, though in this case the entire system is not ergodic and the dynamics are qualitatively rather different as a consequence.
the function here is not unconditionally almost periodic, though in this case the entire system is not ergodic and the dynamics are qualitatively rather different as a consequence.
4 June, 2023 at 7:43 am
Matk
A question related to the comment before the Example 1. is a factor of
is a factor of  with the corresponding factor map
with the corresponding factor map  , then
, then  is obviously another factor of
is obviously another factor of  . I’ve seen being claimed (for example, in your paper with Bergelson and Ziegler, Remark 1.8 in https://arxiv.org/pdf/0901.2602.pdf) that all factors are, up to isomorphism, are of this type, i.e. isomorphic to the original space but with a smaller
. I’ve seen being claimed (for example, in your paper with Bergelson and Ziegler, Remark 1.8 in https://arxiv.org/pdf/0901.2602.pdf) that all factors are, up to isomorphism, are of this type, i.e. isomorphic to the original space but with a smaller  -algebra. Is this really true? What is the meaning of “isomorphic” here, i.e. is in the sense of
-algebra. Is this really true? What is the meaning of “isomorphic” here, i.e. is in the sense of 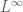 algebras? I don’t see how it can be isomorphic in the usual category of measure-preserving systems, given that
algebras? I don’t see how it can be isomorphic in the usual category of measure-preserving systems, given that  can be much smaller than
can be much smaller than  and thus impossible to be the its extension (even with smaller
and thus impossible to be the its extension (even with smaller  -algebra on
-algebra on  and discarding null-sets).
and discarding null-sets).
Let
4 June, 2023 at 10:20 am
Terence Tao
Yes, isomorphism is in the sense of isomorphic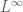 algebras (equipped with a trace and a shift), or equivalently as probability algebras. See for instance this more recent paper (particularly Appendix A) of Jamneshan, Shalom and myself for some discussion, and this foundational paper of Jamneshan and myself for a much more detailed dive into this topic.
algebras (equipped with a trace and a shift), or equivalently as probability algebras. See for instance this more recent paper (particularly Appendix A) of Jamneshan, Shalom and myself for some discussion, and this foundational paper of Jamneshan and myself for a much more detailed dive into this topic.