The famous Gödel completeness theorem in logic (not to be confused with the even more famous Gödel incompleteness theorem) roughly states the following:
Theorem 1 (Gödel completeness theorem, informal statement) Let
be a first-order theory (a formal language
, together with a set of axioms, i.e. sentences assumed to be true), and let
be a sentence in the formal language. Assume also that the language
has at most countably many symbols. Then the following are equivalent:
- (i) (Syntactic consequence)
can be deduced from the axioms in
by a finite number of applications of the laws of deduction in first order logic. (This property is abbreviated as
.)
- (ii) (Semantic consequence) Every structure
which satisfies or models
, also satisfies
. (This property is abbreviated as
.)
- (iii) (Semantic consequence for at most countable models) Every structure
which is at most countable, and which models
, also satisfies
.
One can also formulate versions of the completeness theorem for languages with uncountably many symbols, but I will not do so here. One can also force other cardinalities on the model by using the Löwenheim-Skolem theorem.
To state this theorem even more informally, any (first-order) result which is true in all models of a theory, must be logically deducible from that theory, and vice versa. (For instance, any result which is true for all groups, must be deducible from the group axioms; any result which is true for all systems obeying Peano arithmetic, must be deducible from the Peano axioms; and so forth.) In fact, it suffices to check countable and finite models only; for instance, any first-order statement which is true for all finite or countable groups, is in fact true for all groups! Informally, a first-order language with only countably many symbols cannot “detect” whether a given structure is countably or uncountably infinite. Thus for instance even the ZFC axioms of set theory must have some at most countable model, even though one can use ZFC to prove the existence of uncountable sets; this is known as Skolem’s paradox. (To resolve the paradox, one needs to carefully distinguish between an object in a set theory being “externally” countable in the structure that models that theory, and being “internally” countable within that theory.)
Of course, a theory may contain undecidable statements
– sentences which are neither provable nor disprovable in the theory. By the completeness theorem, this is equivalent to saying that
is satisfied by some models of
but not by other models. Thus the completeness theorem is compatible with the incompleteness theorem: recursively enumerable theories such as Peano arithmetic are modeled by the natural numbers
, but are also modeled by other structures also, and there are sentences satisfied by
which are not satisfied by other models of Peano arithmetic, and are thus undecidable within that arithmetic.
An important corollary of the completeness theorem is the compactness theorem:
Corollary 2 (Compactness theorem, informal statement) Let
be a first-order theory whose language has at most countably many symbols. Then the following are equivalent:
- (i)
is consistent, i.e. it is not possible to logically deduce a contradiction from the axioms in
.
- (ii)
is satisfiable, i.e. there exists a structure
that models
.
- (iii) There exists a structure
which is at most countable, that models
.
- (iv) Every finite subset
of
is consistent.
- (v) Every finite subset
of
is satisfiable.
- (vi) Every finite subset
of
is satisfiable with an at most countable model.
Indeed, the equivalence of (i)-(iii), or (iv)-(vi), follows directly from the completeness theorem, while the equivalence of (i) and (iv) follows from the fact that any logical deduction has finite length and so can involve at most finitely many of the axioms in . (Again, the theorem can be generalised to uncountable languages, but the models become uncountable also.)
There is a consequence of the compactness theorem which more closely resembles the sequential concept of compactness. Given a sequence of structures for
, and another structure
for
, let us say that
converges elementarily to
if every sentence
which is satisfied by
, is also satisfied by
for sufficiently large
. (Replacing
by its negation
, we also see that every sentence that is not satisfied by
, is not satisfied by
for sufficiently large
.) Note that the limit
is only unique up to elementary equivalence. Clearly, if each of the
models some theory
, then the limit
will also; thus for instance the elementary limit of a sequence of groups is still a group, the elementary limit of a sequence of rings is still a ring, etc.
Corollary 3 (Sequential compactness theorem) Let
be a language with at most countably many symbols, and let
be a sequence of structures for
. Then there exists a subsequence
which converges elementarily to a limit
which is at most countable.
Proof: For each structure , let
be the theory of that structure, i.e. the set of all sentences that are satisfied by that structure. One can view that theory as a point in
, where
is the set of all sentences in the language
. Since
has at most countably many symbols,
is at most countable, and so (by the sequential Tychonoff theorem)
is sequentially compact in the product topology. (This can also be seen directly by the usual Arzelá-Ascoli diagonalisation argument.) Thus we can find a subsequence
which converges in the product topology to a limit theory
, thus every sentence in
is satisfied by
for sufficiently large
(and every sentence not in
is not satisfied by
for sufficiently large
). In particular, any finite subset of
is satisfiable, hence consistent; by the compactness theorem,
itself is therefore consistent, and has an at most countable model
. Also, each of the theories
is clearly complete (given any sentence
, either
or
is in the theory), and so
is complete as well. One concludes that
is the theory of
, and hence
is the elementary limit of the
as claimed.
[It is also possible to state the compactness theorem using the topological notion of compactness, as follows: let be the space of all structures of a given language
, quotiented by elementary equivalence. One can define a topology on
by taking the sets
as a sub-base, where
ranges over all sentences. Then the compactness theorem is equivalent to the assertion that
is topologically compact.]
One can use the sequential compactness theorem to build a number of interesting “non-standard” models to various theories. For instance, consider the language used by Peano arithmetic (which contains the operations
and the successor operation
, the relation
, and the constant
), and adjoint a new constant
to create an expanded language
. For each natural number
, let
be a structure for
which consists of the natural numbers
(with the usual interpretations of
,
, etc.) and interprets the symbol
as the natural number
. By the compactness theorem, some subsequence of
must converge elementarily to a new structure
of
, which still models Peano arithmetic, but now has the additional property that
for every (standard) natural number
; thus we have managed to create a non-standard model of Peano arithmetic which contains a non-standardly large number (one which is larger than every standard natural number).
The sequential compactness theorem also lets us construct infinitary limits of various sequences of finitary objects; for instance, one can construct infinite pseudo-finite fields as the elementary limits of sequences of finite fields. I recently discovered that other several correspondence principles between finitary and infinitary objects, such as the Furstenberg correspondence principle between sets of integers and dynamical systems, or the more recent correspondence principles concerning graph limits, can be viewed as special cases of the sequential compactness theorem; it also seems possible to encode much of the sum-product theory in finite fields in an infinitary setting using this theorem. I hope to discuss these points in more detail in a later post. In this post, I wish to review (partly for my own benefit) the proof of the completeness (and hence compactness) theorem. The material here is quite standard (I basically follow the usual proof of Henkin, and taking advantage of Skolemisation), but perhaps the concept of an elementary limit is not as well-known outside of logic as it might be. (The closely related concept of an ultraproduct is better known, and can be used to prove most of the compactness theorem already, thanks to Los’s theorem, but I do not know how to use ultraproducts to ensure that the limiting model is countable. However, one can think (intuitively, at least), of the limit model in the above theorem as being the set of “constructible” elements of an ultraproduct of the
.)
In order to emphasise the main ideas in the proof, I will gloss over some of the more technical details in the proofs, relying instead on informal arguments and examples at various points.
— 1. Completeness and compactness in propositional logic —
The completeness and compactness theorems are results in first-order logic. But to motivate some of the ideas in proving these theorems, let us first consider the simpler case of propositional logic. The language of a propositional logic consists of the following:
- A finite or infinite collection
of propositional variables – atomic formulae which could be true or false, depending on the interpretation;
- A collection of logical connectives, such as conjunction
, disjunction
, negation
, or implication
. (The exact choice of which logical connectives to include in the language is to some extent a matter of taste.)
- Parentheses (in order to indicate the order of operations).
Of course, we assume that the symbols used for atomic formulae are distinct from those used for logical connectives, or for parentheses; we will implicitly make similar assumptions of this type in later sections without further comment.
Using this language, one can form sentences (or formulae) by some standard formal rules which I will not write down here. Typical examples of sentences in propositional logic are ,
, and
. Each sentence is of finite length, and thus involves at most finitely many of the propositional variables. Observe that if
is at most countable, then there are at most countably many sentences.
The analogue of a structure in propositional logic is a truth assignment. A truth assignment for a propositional language
consists of a truth value
assigned to each propositional variable
. (Thus, for instance, if there are
propositional variables in the language, then there are
possible truth assignments.) Once a truth assignment
has assigned a truth value
to each propositional variable
, it can then assign a truth value
to any other sentence
in the language
by using the usual truth tables for conjunction, negation, etc.; we write
if
assigns a true value to
(and say that
is satisfied by
), and
otherwise. Thus, for instance, if
and
, then
and
, but
. Some sentences, e.g.
, are true in every truth assignment; these are the (semantic) tautologies. At the other extreme, the negation of a tautology will of course be false in every truth assignment.
A theory is a language
, together with a (finite or infinite) collection of sentences (also called
) in that language. A truth assignment
satisfies (or models) the theory
, and we write
, if we have
for all
. Thus, for instance, if
is as in the preceding example and
, then
.
The analogue of the Gödel completeness theorem is then
Theorem 4 (Completeness theorem for propositional logic) Let
be a theory for a propositional language
, and let
be a sentence in
. Then the following are equivalent:
- (i) (Syntactic consequence)
can be deduced from the axioms in
by a finite number of applications of the laws of propositional logic.
- (ii) (Semantic consequence) Every truth assignment
which satisfies (or models)
, also satisfies
.
One can list a complete set of laws of propositional logic used in (i), but we will not do so here.
To prove the completeness theorem, it suffices to show the following equivalent version.
Theorem 5 (Completeness theorem for propositional logic, again) Let
be a theory for a propositional language
. Then the following are equivalent:
- (i)
is consistent, i.e. it is not possible to logically deduce a contradiction from the axioms in
.
- (ii)
is satisfiable, i.e. there exists a truth assignment
that models
.
Indeed, Theorem 4 follows from Theorem 5 by applying Theorem 5 to the theory and taking contrapositives.
It remains to prove Theorem 5. It is easy to deduce (i) from (ii), because the laws of propositional logic are sound: given any truth assignment, it is easy to verify that these laws can only produce true conclusions given true hypotheses. The more interesting implication is to obtain (ii) from (i) – given a consistent theory , one needs to produce a truth assignment that models that theory.
Let’s first consider the case when the propositional language is finite, so that there are only finitely many propositional variables
. Then we can argue using the following “greedy algorithm”.
- We begin with a consistent theory
.
- Observe that at least one of
or
must be consistent. For if both
and
led to a logical contradiction, then by the laws of logic one can show that
must also lead to a logical contradiction.
- If
is consistent, we set
and
; otherwise, we set
and
.
is consistent, so arguing as before we know that at least one of
or
must be consistent. If the former is consistent, we set
and
; otherwise set
and
.
- We continue in this fashion, eventually ending up with a consistent theory
containing
, and a complete truth assignment
such that
whenever
is such that
, and such that
whenever
is such that
.
- From the laws of logic and an induction argument, one then sees that if
is any sentence with
, then
is a logical consequence of
, and hence (since
is consistent)
is not a consequence of
. Taking contrapositives, we see that
whenever
is a consequence of
; replacing
by
we conclude that
satisfies every sentence in
, and the claim follows.
Remark 1 The above argument shows in particular that any finite theory either has a model or a proof of a contradictory statement (such as
). Actually producing a model if it exists, though, is essentially the infamous satisfiability problem, which is known to be NP-complete, and thus (if
) would require super-polynomial time to execute.
The case of an infinite language can be obtained by combining the above argument with Zorn’s lemma (or transfinite induction and the axiom of choice, if the set of propositional variables happens to be well-ordered). Alternatively, one can proceed by establishing
Theorem 6 (Compactness theorem for propositional logic) Let
be a theory for a propositional language
. Then the following are equivalent:
- (i)
is satisfiable.
- (ii) Every finite subset
of
is satisfiable.
It is easy to see that Theorem 6 will allow us to use the finite case of Theorem 5 to deduce the infinite case, so it remains to prove Theorem 6. The implication of (ii) from (i) is trivial; the interesting implication is the converse.
Observe that there is a one-to-one correspondence between truth assignments and elements of the product space
, where
is the set of propositional variables. For every sentence
, let
be the collection of all truth assignments that satisfy
; observe that this is a closed (and open) subset of
in the product topology (basically because
only involves finitely many of the propositional variables). If every finite subset
of
is satisfiable, then
is non-empty; thus the family
of closed sets enjoys the finite intersection property. On the other hand, from Tychonoff’s theorem,
is compact. We conclude that
is non-empty, and the claim follows.
Remark 2 While Tychonoff’s theorem in full generality is equivalent to the axiom of choice, it is possible to prove the compactness theorem using a weaker version of this axiom, namely the ultrafilter lemma. In fact, the compactness theorem is logically equivalent to this lemma.
— 2. Zeroth-order logic —
Propositional logic is far too limited a language to do much mathematics. Let’s make the language a bit more expressive, by adding constants, operations, relations, and (optionally) the equals sign; however, we refrain at this stage from adding variables or quantifiers, making this a zeroth-order logic rather than a first-order one.
A zeroth-order language consists of the following objects:
- A (finite or infinite) collection
of propositional variables;
- A collection
of relations (or predicates), with each
having an arity (or valence)
(e.g. unary relation, binary relation, etc.);
- A collection
of constants;
- A collection
of operators (or functions), with each operator
having an arity
(e.g. unary operator, binary operator, etc.);
- Logical connectives;
- Parentheses;
- Optionally, the equals sign
.
For instance, a zeroth-order language for arithmetic on the natural numbers might include the constants , the binary relations
, the binary operations
, the unary successor operation
, and the equals sign
. A zeroth-order language for studying all groups generated by six elements might include six generators
and the identity element
as constants, as well as the binary operation
of group multiplication and the unary operation
of group inversion, together with the equals sign
. And so forth.
Note that one could shorten the description of such languages by viewing propositional variables as relations of arity zero, and similarly viewing constants as operators of arity zero, but I find it conceptually clearer to leave these two operations separate, at least initially. As we shall see shortly, one can also essentially eliminate the privileged role of the equals sign by treating it as just another binary relation, which happens to have some standard axioms attached to it.
By combining constants and operators together in the usual fashion one can create terms; for instance, in the zeroth-order language for arithmetic, is a term. By inserting terms into a predicate or relation (or the equals sign
), or using a propositional variable, one obtains an atomic formula; thus for instance
is an atomic formula. By combining atomic formulae using logical connectives, one obtains a sentence (or formula); thus for instance
is a sentence.
In order to assign meaning to sentences, we need the notion of a structure for a zeroth-order language
. A structure consists of the following objects:
- A domain of discourse (or universe of discourse)
;
- An assignment of a value
to every constant
;
- An assignment of a function
to every operation
;
- An assignment of a truth value
to every propositional variable
;
- An assignment of a function
to every relation
.
For instance, if is the language of groups with six generators discussed above, then a structure
would consist of a set
, seven elements
in that set, a binary operation
, and a unary operation
. At present, no group-type properties are assumed on these operations; the structure here is little more than a magma at this point.
Every sentence in a zeroth-order language
can be interpreted in a structure
for that language to give a truth value
, simply by substituting all symbols
in the language with their interpreted counterparts
(note that the equals sign
does not need any additional data in order to be interpreted). For instance, the sentence
is true in
if
. Similarly, every term
in the language can be interpreted to give a value
in the domain of discourse
.
As before, a theory is a collection of sentences; we can define satisfiability ,
of a sentence
or a theory
by a structure
just as in the previous section. For instance, to describe groups with at most six generators in the language
, one might use the theory
which consists of all the group axioms, specialised to terms, e.g.
would contain the associativity axioms
for all choices of terms
. (Note that this theory is not quite strong enough to capture the concept of a structure
being a group generated by six elements, because the domain of
may contain some “inaccessible” elements which are not the interpretation of any term in
, but without the universal quantifier, there is not much we can do in zeroth-order logic to say anything about those elements, and so this is pretty much the best we can do with this limited logic.)
Now we can state the completeness theorem:
Theorem 7 (Completeness theorem for zeroth-order logic) Let
be a theory for a zeroth-order language
, and let
be a sentence in
. Then the following are equivalent:
- (i) (Syntactic consequence)
can be deduced from the axioms in
by a finite number of applications of the laws of zeroth-order logic (i.e. all the laws of first-order logic that do not involve variables or quantifiers).
- (ii) (Semantic consequence) Every truth assignment
which satisfies (or models)
, also satisfies
.
To prove this theorem, it suffices as before to show that every consistent theory in a zeroth-order logic is satisfiable, and conversely. The converse implication is again straightforward (the laws of zeroth-order logic are easily seen to be sound); the main task is to show the forward direction, i.e.
Proposition 8 Let
be a consistent zeroth-order theory. Then
has at least one model.
Proof: It is convenient to begin by eliminating the equality symbol from the language. Suppose we have already proven Proposition 8 has already been shown for languages without the equality symbol. Then we claim that the proposition also holds for languages with the equality symbol. Indeed, given a consistent theory in a language
with equality, we can form a companion theory
in the language
formed by removing the equality symbol from
and replacing it with a new binary relation
, by taking all the sentences in
and replacing
by
, and then adding in all the axioms of equality (with
replaced by
) to
. Thus, for instance, one would add the transitivity axioms
to
for each triple of terms
, as well as substitution axioms such as
for any terms
and binary functions
. It is straightforward to verify that if
is consistent, then
is also consistent, because any contradiction derived in
can be translated to a contradiction derived in
simply by replacing
with
throughout and using the axioms of equality. By hypothesis, we conclude that
has some model
. By the axioms of equality, the interpretation
of
in this model is then an equivalence relation on the domain
of
. One can also remove from the domain of
any element which is not of the form
for some term
, as such “inaccessible” elements will not influence the satisfiability of
. We can then define a structure
for the original language
by quotienting the domain of
by the equivalence relation
, and also quotienting all the interpretations of the relations and operations of
; the axioms of equality ensure that this quotienting is possible, and that the quotiented structure
satisfies
; we omit the details.
Henceforth we assume that does not contain the equality sign. We will then choose a “tautological” domain of discourse
, by setting this domain to be nothing more than the collection of all terms in the language
. For instance, in the language of groups on six generators, the domain
is basically the free magma (with “inverse”) on six generators plus an “identity”, consisting of terms such as
,
, etc. With this choice of domain, there is an obvious “tautological” interpretation of constants (
) and operations (e.g.
for binary operations
and terms
), which leads to every term
being interpreted as itself:
.
It remains to figure out how to interpret the propositional variables and relations
. Actually, one can replace each relation with an equivalent collection of new propositional variables by substituting in all possible terms in the relation. For instance, if one has a binary relation
, one can replace this single relation symbol in the language by a (possibly infinite) collection of propositional variables
, one for each pair of terms
, leading to a new (and probably much larger) language
without any relation symbols. It is not hard to see that if theory
is consistent in
, then the theory
in
formed by interpreting all atomic formulae such as
as propositional variables is also consistent. If
has a model
with the tautological domain of discourse, it is not hard to see that this can be converted to a model
of
with the same domain by defining the interpretation
of relations
in the obvious manner.
So now we may assume that there are no relation symbols, so that now consists entirely of propositional sentences involving the propositional variables. But the claim now follows from the completeness theorem in propositional logic.
Remark 3 The above proof can be viewed as a combination of the completeness theorem in propositional logic and the familiar procedure in algebra of constructing an algebraic object (e.g. a group) that obeys various relations, by starting with the free version of that object (e.g. a free group) and then quotienting out by the equivalence relation generated by those relations.
Remark 4 Observe that if
is at most countable, then the structures
constructed by the above procedure are at most countable (because the set of terms is at most countable, and quotienting by an equivalence relation cannot increase the cardinality). Thus we see (as in Theorem 1 or Corollary 2) that if a zeroth-order theory in an at most countable language is satisfiable, then it is in fact satisfiable with an at most countable model.
From the completeness theorem for zeroth-order logic and the above remark we obtain the compactness theorem for zeroth-order logic, which is formulated exactly as in Corollary 2.
— 3. First-order logic —
We are now ready to study languages which are expressive enough to do some serious mathematics, namely the languages of first-order logic, which are formed from zeroth-order logics by adding variables and quantifiers. (There are higher-order logics as well, but unfortunately the completeness and compactness theorems typically fail for these, and they will not be discussed here.)
A language for a first-order logic consists of the following:
- A (finite or infinite) collection
of propositional variables;
- A collection
of relations, with each
having an arity
;
- A collection
of constants;
- A collection
of operators, with each
having an arity
;
- A collection
of variables;
- Logical connectives;
- The quantifiers
;
- Parentheses;
- Optionally, the equals sign
.
For instance, the language for Peano arithmetic includes a constant , a unary operator
, binary operators
, the equals sign
, and a countably infinite number of variables
.
By combining constants, variables and operators together one creates terms; by inserting terms into predicates or relations, or using propositional variables, one obtains atomic formulae. These atomic formulae can contain a number of free variables. Using logical connectives as well as quantifiers to bind any or all of these variables, one obtains well-formed formulae; a formula with no free variables is a sentence. Thus, for instance, is a well-formed formula, and
is a sentence.
A structure for a first-order language
is exactly the same concept as for a zeroth-order language: a domain of discourse, together with an interpretation of all the constants, operators, propositional variables, and relations in the language. Given a structure
, one can interpret terms
with no free variables as elements
of
, and interpret sentences
as truth values
, in the standard fashion.
A theory is, once again, a collection of sentences in the first-order language ; one can define what it means for a structure to satisfy a sentence or a theory just as before.
Remark 5 In most fields of mathematics, one wishes to discuss several types of objects (e.g. numbers, sets, points, group elements, etc.) at once. For this, one would prefer to use a typed language, in which variables, constants, and functions take values in one type of object, and relations and functions take only certain types of objects as input. However, one can easily model a typed theory using a typeless theory by the trick of adding some additional unary predicates to capture type (e.g.
to indicate the assertion “
is a natural number”,
to indicate the assertion “
is a set”, etc.) and modifying the axioms of the theory being considered accordingly. (For instance, in a language involving both natural numbers and other mathematical objects, one might impose a new closure axiom
, and axioms such as the commutativity axiom
would need to be modified to
.) It is a tedious but routine matter to show that the completeness and compactness theorems for typeless first-order logic imply analogous results for typed first-order logic; we omit the details.
To prove the completeness (and hence compactness) theorem, it suffices as before to show that
Proposition 9 Let
be a consistent first-order theory, with an at most countable language
. Then
has at least one model
, which is also at most countable.
We shall prove this result using a series of reductions. Firstly, we can mimic the arguments in the zeroth-order case and reduce to the case when does not contain the equality symbol. (We no longer need to restrict the domain of discourse to those elements which can be interpreted by terms, because the universal quantifier
is now available for use when stating the axioms of equality.) Henceforth we shall assume that the equality symbol is not present in the language.
Next, by using the laws of first-order logic to push all quantifiers in the sentences in to the beginning (e.g. replacing
with
) one may assume that all sentences in
are in prenex normal form, i.e. they consist of a “matrix” of quantifiers, followed by an quantifier-free formula – a well-formed formula with no quantifiers. For instance,
is in prenex normal form, where
is an quantifier-free formula with four free variables
.
Now we will start removing the existential quantifiers from the sentences in
. Let’s begin with a simple case, when
contains a sentence of the form
for some quantifier-free formula of one free variable
. Then one can eliminate the existential quantifier by introducing a witness, or more precisely adjoining a new constant
to the language
and replacing the statement
with the statement
, giving rise to a new theory
in a new language
. The consistency of
easily implies the consistency of
, while any at most countable model for
can be easily converted to an at most countable model for
(by “forgetting” the symbol
). (In fact,
is a conservative extension of
.) We can apply this reduction simultaneously to all sentences of the form
in
(thus potentially expanding the collection of constants in the language by a countable amount).
The same argument works for any sentence in prenex normal form in which all the existential quantifiers are to the left of the universal quantifiers, e.g. ; this statement requires two constants to separately witness
and
, but otherwise one proceeds much as in the previous paragraph. But what about if one or more of the existential quantifiers is buried behind a universal quantifier? The trick is then to use Skolemisation. We illustrate this with the simplest case of this type, namely that of a sentence
. Here, one cannot use a constant witness for
. But this is no problem: one simply introduces a witness that depends on
. More precisely, one adjoins a new unary operator
to the language
and replaces the statement
by
, creating a new theory
in a new language
. One can again show (though this is not entirely trivial) that the consistency of
implies the consistency of
, and that every countable model for
can be converted to a countable model for
(again by “forgetting”
). So one can eliminate the existential quantifier from this sentence also. Similar methods work for any other prenex normal form; for instance with the sentence
one can obtain a conservative extension of that theory by introducing a unary operator and a binary operator
and replacing the above sentence with
One can show that one can perform Skolemisation on all the sentences in simultaneously, which has the effect of eliminating all existential quantifiers from
while still keeping the language
at most countable (since
is at most countable). (Intuitively, what is going on here is that we are interpreting all existential axioms in the theory as implicitly defining functions, which we then explicitly formalise as a new symbol in the language. For instance, if we had some theory of sets which contained the axiom of choice (every family of non-empty sets
admits a choice function
), then we can Skolemise this by introducing a “choice function function”
that witnessed this axiom to the language. Note that we do not need uniqueness in the existential claim in order to be able to perform Skolemisation.)
After performing Skolemisation and adding all the witnesses to the language, we are reduced to the case in which all the sentences in are in fact universal statements, i.e. of the form
, where
is an quantifier-free formula of
free variables. In this case one can repeat the zeroth-order arguments, selecting a structure
whose domain of discourse is the tautological one, indexed by all the terms with no free variables (in particular, this structure will be countable). One can then replace each first-order statement
in
by the family of zeroth-order statements
, where
ranges over all terms with no free variables, thus creating a zeroth-order theory
. As
is consistent,
is also, so by the zeroth-order theory, we can find a model
for
with the tautological domain of discourse, and it is clear that this structure will also be a model for the original theory
. The proof of the completeness theorem (and thus the compactness theorem) is now complete.
In summary: to create a countable model from a consistent first-order theory, one first replaces the equality sign (if any) by a binary relation
, then uses Skolemisation to make all implied functions and operations explicit elements of the language. Next, one makes the zeroth-order terms of the new language the domain of discourse, applies a greedy algorithm to decide the truth assignment of all zeroth-order sentences, and then finally quotients out by the equivalence relation given by
to recover the countable model.
Remark 6 I find the use of Skolemisation to greatly clarify, at a conceptual level, the proof of the completeness theorem. However, at a technical level it does make things more complicated: in particular, showing that the Skolemisation of a consistent theory is still consistent does require some non-trivial effort (one has to take all arguments involving the Skolem function
, and replace every occurence of
by a “virtual” function, defined implicitly using existential quantifiers). On the other hand, this fact is easy to prove once one already has the completeness theorem, though we of course cannot formally take advantage of this while trying to prove that theorem!
The more traditional Henkin approach is based instead on adding a large number of constant witnesses, one for every existential statement: roughly speaking, for each existential sentence
in the language, one adds a new constant
to the language and inserts an axiom
to the theory; it is easier to show that this preserves consistency than it is with a more general Skolemisation. Unfortunately, every time one adds a constant to the language, one increases the number of existential sentences for which one needs to perform this type of witnessing, but it turns out that after applying this procedure a countable number of times, one can get to the point where every existential sentence is automatically witnessed by some constant. This has the same ultimate effect as Skolemisation, namely one can convert sentences containing existential quantifiers to ones which are purely universal, and so the rest of the proof is much the same as the proof described above. On the other hand, the Henkin approach avoids the axiom of choice (though one still must use the ultrafilter lemma, of course).

50 comments
Comments feed for this article
10 April, 2009 at 9:49 pm
Gödel, Hilbert and Brouwer « Combinatorics and more
[…] For a technical discussions of Gödel’s completeness and compactness theorem, see this post by Terry Tao. Possibly related posts: (automatically generated)About MathematicsWhy […]
11 April, 2009 at 6:49 am
Eric
In the paragraph before Corollary 2, you give the nonstandard natural numbers as an example of how theories of arithmetic are incomplete. However, the nonstandard natural numbers are intentionally constructed to be elementarily equivalent to the natural numbers. Indeed, they witness not the fact that recursively enumerable theories of arithmetic are incomplete but that any first-order theory has “nonstandard”, large models (say, by upward Lowenheim-Skolem).
11 April, 2009 at 8:20 am
Terence Tao
Ah, good point. I suppose it is difficult to construct an example of a model of arithmetic that is not elementarily equivalent to N without going through most of the proof of the incompleteness theorem already, so I guess I will have to omit an example altogether in this paragraph…
11 April, 2009 at 10:55 am
Anonymous
I am always curious about the motivation of these expository posts. Any self-motivated mathematician is always interested to learn new material (I have a growing mountain of “to read” papers on my desk). However, there always seems to be more pressing demands. For example, your previous work (and blog posts) suggest that you are currently part way through very promising (landmark?) projects related to the (1) regularity of wave maps, and (2) linear equations in the primes. Undoubtedly, you have other ongoing projects and professional responsibilies as well. So, I’m intrigued by the fact that you wake up one morning and say “I’m going to put major projects X,Y,Z,X’,Y’,Z’,etc on hold, while I learn about first-order logic.” This is, of course, curiosity and not criticism. This method obviously works for you.
11 April, 2009 at 11:17 am
Anonymous
That is great,
thanks
11 April, 2009 at 12:19 pm
Anonymous
Just a little remark regarding extensions of first order logic:
You wrote:
“There are higher-order logics as well, but unfortunately the completeness and compactness theorems fail for these, and they will not be discussed here.”
In fact, by Lindstrom’s theorem, first order logic is the strongest logic that has the compactness property and the Lowenheim-Skolem property at Aleph_0. But it turns out that you can still work with a logic that is considerably stronger than FOL and yet is pretty much well-behaved, for example, Shelah’s extensions of FOL with cofinality quantifiers has the compactness property and LS property for Aleph_1.
There is a nice expository paper by Barwise on this subject which can be found here: http://www.math.ucla.edu/~asl/bsl/1001/1001-004.ps
11 April, 2009 at 2:17 pm
Terence Tao
Dear Anonymous #1,
Actually, in many ways this post was indirectly motivated by the projects (1) and (2) you mention (I have been working on (1) this week, and was working on (2) a couple weeks ago, as these are indeed my two major projects), even though there is no direct connection in subject matter. A few weeks ago, in discussions with a colleague, I realised that the compactness theorem may have some relevance to yet another question I was interested in; but as I wanted to clear the way to return to my main projects, I decided to at least figure out to my satisfaction once and for all how the compactness theorem worked, so I could return to it later when there is some natural break in my other projects. [I also find that I need to intersperse some relatively basic projects such as these (or such as my class notes) between major research efforts, to avoid getting mentally exhausted or frustrated.] I do plan to write a post later regarding my motivation for looking at the compactness theorem, but this may have to wait for a more opportune time.
Dear Anonymous #3: thanks for the link! I think I will tone down “fail” to “typically fail’, given that there are indeed some higher-order logics for which some version of completeness or compactness holds.
12 April, 2009 at 12:38 am
anon
Thanks for the very interesting blog entry! Very well written for someone who has never attended a lecture in logic.
I’ve got a question for (ii) => (i) in Corollary 2: I don’t see how it immediately follows from Theorem 1 (ii) => (i) because in Cor. 2 I only have “there exists a structure …”, but in Thm. 1 I need “every structure …”.
12 April, 2009 at 12:55 am
anon
Ok, I guess I have to do something similiar to Thm 5 => Thm 4.
12 April, 2009 at 7:22 pm
mistar grape
What sort of “more recent correspondence principles concerning graph limits” are yah talking about here? Is this the elek&szegedy paper, or something else?
13 April, 2009 at 7:18 pm
Kelly Johnson
Thanks, Terence. I appreciated the response to Anonymous #1, as I’ve often wondered that myself. It’s always encouraging to get your thoughts on time management since there never seems to be enough time in the day!
19 April, 2009 at 5:58 pm
Carson Chow
Hi Terry,
I was wondering if in Theorems 4 and 7, that you meant to write that phi was a sentence in the language L, rather than a sentence in the theory Gamma of the language L.
Thanks,
Carson
[Corrected, thanks – T]
20 April, 2009 at 7:28 am
Jose Brox
Hi Terry! Brilliant post! (As always)
Where could I look up more information about “elementary convergence”?
Also, do you know if it has been applied to (multi)digraphs?
I think this concept is what I was looking for in my ph.D. thesis.
Thanks and kindest regards,
Jose Brox
21 April, 2009 at 6:58 am
John Goodrick
Thanks for posting this! I’m a model theorist and from what I’ve had time to look at so far it looks like a good explanation of the completeness theorem.
Couple of quick comments: first, I found it puzzling that your main results (Theorem 1, Corollary 2, etc.) you insisted that the language be countable. Compactness and completeness as they are normally stated (i.e. Theorem 1, parts (i) and (ii)) are true in *any* language, countable or not, and this is very important in model theory. E.g. the proof that consistent theories with infinite models have models of arbitrarily large cardinality goes by expanding to an uncountable language with lots of new constant symbols and applying Compactness.
Second, I don’t think your notion of “elementary convergence” of a sequence of models well-known even *within* logic. (I think this is the first time I’d heard of it!) I’m not quite sure if they’re good for anything that ultraproducts and reduced products aren’t already good for, but admittedly I haven’t thought about this much.
21 April, 2009 at 10:37 am
Terence Tao
Dear John,
Thanks for the comments. I restricted attention to countable languages in order to get a countable model at the end of the day (and also to simplify the notation a little bit in the proof) but of course the theorems extend to higher cardinalities (but now the cardinality of the model will be as large as the cardinality of the language). I had a little remark about this after Theorem 1, but can expand upon this. [Also, I think once one moves to uncountable languages, one loses sequential compactness of theories, though one still has topological compactness by Tychonoff’s theorem.]
Every ultraproduct of a sequence of structures is an elementary limit of those structures (Los’ theorem), so yes, ultraproducts can already do most of what elementary limits can do. The one thing which is nice about going through the completeness and/or Lowenheim-Skolem theorem, though is that one can get a countable elementary limit (which would correspond to restricting the ultraproduct to “constructible” elements of that ultraproduct, I think.)
23 April, 2009 at 9:01 am
John Goodrick
OK, now I see that you’re really proving Compactness plus downward Lowenheim-Skolem simultaneously, which is neat (this isn’t how I normally see it done).
I stand by an earlier point, though: your argument in Proposition 9 really has nothing at all to do with the countability of the language! Given any consistent theory T, there is always a consistent Skolemization T’ of T of size at most [cardinality of T] plus aleph-0, and the rest of your argument goes through from there.
4 May, 2009 at 6:59 pm
nhung
i from viet nam.i can’t speak and wrtte english.i like math.but i learn no good.i amide you.sorry becauce i’m to bother you
5 May, 2009 at 7:59 pm
zk
It’s a great blog for learning.
8 May, 2009 at 8:14 pm
Szemeredi’s regularity lemma via the correspondence principle « What’s new
[…] and Szegedy. It also seems to be related to the concept of an elementary limit that I discussed in this post, though this connection is still rather […]
14 May, 2009 at 6:55 am
Ernie Cohen
A few comments. First, while AC (or equivalently, Tychonoff’s theorem) is typically used to prove the compactness theorem, you should note that it follows from (and is in fact equivalent to) the strictly weaker untrafilter lemma.
Second, in remark 1 you state “The above argument shows in particular that any finite theory either has a model or a proof that the theory implies a contradiction. Actually producing one or the other, though is essentially the infamous satisfiability problem, which is known to be NP-complete, and thus (if P \neq NP) would require super-polynomial time to execute.”
There are some technical sloppiness here. While checking for consistency is NP-complete, checking for inconsistency is believed not to be in NP (it is coNP-complete). And checking that the theory is inconsistent is not the same as producing a proof of inconsistency; indeed, every inconsistent theory having a polynomial-size proof would imply NP=coNP.
Third, an advantage of the Henkin approach is that Skolemization assumes AC, whereas the Henkin approach does not.
14 May, 2009 at 3:20 pm
Terence Tao
Dear Ernie: Thanks for the corrections and comments!
6 June, 2009 at 1:33 am
anon
Why is any ultraproduct of a sequence of structures an elementary limit in your sense? I see why Los’ theorem gives unboundedly many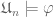 when
when  , but I don’t see why it gives cofinitely many.
, but I don’t see why it gives cofinitely many.
6 June, 2009 at 10:48 am
Terence Tao
Dear anon,
An ultraproduct of a sequence of structures will be the elementary limit of some subsequence, because there are only countably many sentences one needs to check and one can run the usual Arzela-Ascoli type diagonalisation argument.
14 June, 2009 at 1:54 pm
Sequential compactness theorem @ unwanted capture
[…] and then some are expository bits that he writes up for his own edification. I just noticed a post from April about Gödel’s completeness and compactness theorems. From a logician’s […]
5 August, 2009 at 11:09 am
Danny
I was having a debate with someone – in the context of Godel’s proof of the incompleteness theorem – and the questions came up about the countability of statements in a first-order logic. On one hand, I had always – vaguely – understood that the essense of Godel’s proof was that the set of statements was “larger” than the set of provable statements in the same sense that the set of reals was larger than the set of natural numbers. However, given there is a Godel numbering of proofs and a Godel numbering of statements then they must both be countable at most. Is the latter statement correct – that the set of all statements in first-order logic is countable.
Thx in advance for something that is hopefully not too far off topic
6 October, 2009 at 9:25 am
r97124005個人部落格 » Undecidable Sentences
[…] This is some thought after reading : The completeness and compactness theorems of first-order logic […]
15 October, 2009 at 8:16 pm
Reading seminar: “Stable group theory and approximate subgroups”, by Ehud Hrushovski « What’s new
[…] the completeness theorem, a partial type is nothing more than a set of sentences involving which is logically consistent […]
25 January, 2010 at 10:21 pm
Anonymous
Dear Prof. Tao,
if we take a countable collection of ”decidable” subsets of natural numbers, is their union again ”decidable”?
what about arbitrary union?
thanks
28 September, 2010 at 1:43 am
Anonymous
Yes – Every singleton is decidable, and every set of natural numbers is a union of countably many singletons.
30 January, 2010 at 7:08 pm
Ultralimit analysis, and quantitative algebraic geometry « What’s new
[…] . This existence of elementary limits is a manifestation of the compactness theorem in logic; see this earlier blog post for more discussion. So we see that compactness methods and ultrafilter methods are closely […]
25 June, 2010 at 6:43 pm
The uncertainty principle « What’s new
[…] Semantic-syntactic duality Much more generally still, a mathematical theory can either be described internally or syntactically via its axioms and theorems, or externally or semantically via its models. The fundamental connection between the two perspectives is given by the Gödel completeness theorem. […]
7 September, 2010 at 10:51 pm
Blog cua Tao « Sangtaodaphongcach's Blog
[…] The completeness and compactness theorems of first-order logic […]
7 April, 2011 at 4:42 am
Doug Spoonwood
A language for propositional logic (and first-order logic for that matter) need not contain any parentheses. Lukasiewicz’s notation for propositional logic gives us an example, and the founders of “reverse Polish notation” (e. g. Hamblin) gave us another.
19 May, 2011 at 9:11 pm
Epistemic logic, temporal epistemic logic, and the blue-eyed islander puzzle lower bound « What’s new
[…] this claim is in fact a special case of the Gödel completeness theorem, and is discussed in this previous blog post; we also sketch a proof of completeness […]
7 February, 2013 at 2:48 pm
David Struden
Dear Professor Tao,
Thanks you for your post.
I am a student and I had a course on logic from Mendelson’s textbook and it seems to me that what you stated here about completeness theorem is much general than the completeness theorem of Godel that is presented in Mendelson.
As I understand, a first order theory has two sets of axioms: (1) the core set of axioms contains those common logic axioms such as (A -> (B -> A)); and (2) some extra set of axioms depending on each theory (for example, group has its own group axioms).
If the second set of axioms is empty then it is called a PREDICATE CALCULUS.
In Mendelson, Godel’s completeness theorem stated and proved for “predicate calculus” only. This is Godel’s original theorem, is it right?
What you prove here is a completeness theorem for ALL first order theory. Is my understanding correct?
So what you show here is much more general than Godel’s original theorem.
Thank you again for your post. It is very helpful.
9 July, 2014 at 3:31 am
Moe Hirsch
A beautiful exposition.
A small glitch:
In the paragraph before Corollary 3 (Sequential Compactness Theorem), the second sentence has something missing:
“Given a sequence U_1, U_2, . . . be a sequence of structures ”
[Corrected, thanks – T.]
25 October, 2015 at 1:43 pm
Brian
If I want to get my feet wet with further interactions between logic and topology, starting here with why the compactness theorem is called such, where would I go?
One question I am wondering which is not clear to me. Are topological spaces normally associated with languages and first-order theories metrizable? If so what sorts of metrics are out there to describe the “distance” between first-order theories over a fixed language? Or are these topological spaces associated with languages and first-order theories necessarily not metrizable? What implications would that have, if any, on logic?
25 October, 2015 at 1:53 pm
Brian
I’m trying to bring Brouwer’s fixed point theorem(s) to bear on this situation. If some associated topological spaces are metrizable then there might be contractions and with contractions there are things that can be called “maps” of “territory.” The Brouwer fixed point theorem about contractions implies that if a map is at all within the territory, there is exactly one point of overlap between the map and territory. That point must be really interesting…
28 October, 2015 at 1:56 pm
Two old-ish Terry Tao posts about model theory | sylvy's mathsy blog
[…] this which talks about completeness, compactness, zeroth-order logic, and Skolemisation; […]
12 May, 2016 at 1:48 am
Guy Paterson-Jones
In the proof of theorem 6, I think you have used a union symbol where an intersection symbol was intended.
[Corrected, thanks – T.]
6 July, 2016 at 4:51 pm
Wael Amay
here we must be mentioned to important thoery Tarski’s and kurt godel
have inquiers thats helberts project have been asked …namely if we can said there is independce of tuth and false in amathematic statement
21 July, 2016 at 12:24 pm
Mike
This is one of the best expositions of these topics I have ever read. Brisk and clear.
21 July, 2016 at 1:18 pm
Morris W. Hirsch
Dear Whats new:
Please remove me from your mailing list. I don’t want to receive any more comments.
Thank you
7 December, 2017 at 9:38 am
Compactness – bonefactory
[…] https://terrytao.wordpress.com/2009/04/10/the-completeness-and-compactness-theorems-of-first-order-l… […]
12 December, 2017 at 2:46 am
Consciousness – bonefactory
[…] https://terrytao.wordpress.com/2009/04/10/the-completeness-and-compactness-theorems-of-first-order-l… […]
24 May, 2020 at 8:09 am
OwenH
Regarding the completeness of infinite languages, you say that it can be proved ‘… if the set of propositional variables happens to be well-ordered).’
In what sense is the collection of propositional variables a set? I am wondering if the axiom of choice can be applied to collections of things in general.
26 May, 2020 at 1:50 pm
Terence Tao
The axiom of choice is indeed only limited to sets (Zorn’s lemma, for instance, fails for proper classes). The standard trick here is to restrict the available pool of variables to one that is obviously a set, e.g., by only permitting variables arising from adjoining a finite number of primes to the base symbol
arising from adjoining a finite number of primes to the base symbol  (or if one needs a larger pool of variables, one can only permit variables of the form
(or if one needs a larger pool of variables, one can only permit variables of the form 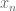 where
where  ranges up to some given ordinal.)
ranges up to some given ordinal.)
15 April, 2022 at 11:18 am
J
How does one define the notion of “countable” in a meta-theory such as Theorem 1? (If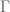 , say, is ZFC, then it cannot be the “countable” in set theory, can it?) Or is such a notion left undefined or primitive?
, say, is ZFC, then it cannot be the “countable” in set theory, can it?) Or is such a notion left undefined or primitive?
19 April, 2022 at 9:02 am
Terence Tao
When establishing metamathematical results such as the completeness theorem, it is understood that the metatheory is expressive enough to handle standard mathematical concepts such as countability. For instance, one can use ZFC for the metatheory if one desires, even if the internal theory one is studying with this metatheory is also ZFC. (This would be somewhat analogous to the practice of self-hosting a compiler in software engineering, i.e., of writing a compiler for a programming language, such as C++, in that very same language.) But to avoid confusion and the perception of infinite regress, one can take the metatheory to be the informal mode of mathematical reasoning that the majority of human mathematicians actually use in practice, rather than any rigid formalization of that reasoning (such as First order Logic + ZFC) that one studies in logic (or which one uses in formal proof verification software).
16 September, 2023 at 9:47 pm
gamalf123
Shouldn’t the example-theory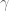 given right before theorem 4 actually consist of
given right before theorem 4 actually consist of  to be considered ‘satisfied’ by the example-truth assignment
to be considered ‘satisfied’ by the example-truth assignment  ?
?
[Corrected, thanks – T.]