This is the third in a series of posts on the “no self-defeating object” argument in mathematics – a powerful and useful argument based on formalising the observation that any object or structure that is so powerful that it can “defeat” even itself, cannot actually exist. This argument is used to establish many basic impossibility results in mathematics, such as Gödel’s theorem that it is impossible for any sufficiently sophisticated formal axiom system to prove its own consistency, Turing’s theorem that it is impossible for any sufficiently sophisticated programming language to solve its own halting problem, or Cantor’s theorem that it is impossible for any set to enumerate its own power set (and as a corollary, the natural numbers cannot enumerate the real numbers).
As remarked in the previous posts, many people who encounter these theorems can feel uneasy about their conclusions, and their method of proof; this seems to be particularly the case with regard to Cantor’s result that the reals are uncountable. In the previous post in this series, I focused on one particular aspect of the standard proofs which one might be uncomfortable with, namely their counterfactual nature, and observed that many of these proofs can be largely (though not completely) converted to non-counterfactual form. However, this does not fully dispel the sense that the conclusions of these theorems – that the reals are not countable, that the class of all sets is not itself a set, that truth cannot be captured by a predicate, that consistency is not provable, etc. – are highly unintuitive, and even objectionable to “common sense” in some cases.
How can intuition lead one to doubt the conclusions of these mathematical results? I believe that one reason is because these results are sensitive to the amount of vagueness in one’s mental model of mathematics. In the formal mathematical world, where every statement is either absolutely true or absolutely false with no middle ground, and all concepts require a precise definition (or at least a precise axiomatisation) before they can be used, then one can rigorously state and prove Cantor’s theorem, Gödel’s theorem, and all the other results mentioned in the previous posts without difficulty. However, in the vague and fuzzy world of mathematical intuition, in which one’s impression of the truth or falsity of a statement may be influenced by recent mental reference points, definitions are malleable and blurry with no sharp dividing lines between what is and what is not covered by such definitions, and key mathematical objects may be incompletely specified and thus “moving targets” subject to interpretation, then one can argue with some degree of justification that the conclusions of the above results are incorrect; in the vague world, it seems quite plausible that one can always enumerate all the real numbers “that one needs to”, one can always justify the consistency of one’s reasoning system, one can reason using truth as if it were a predicate, and so forth. The impossibility results only kick in once one tries to clear away the fog of vagueness and nail down all the definitions and mathematical statements precisely. (To put it another way, the no-self-defeating object argument relies very much on the disconnected, definite, and absolute nature of the boolean truth space in the rigorous mathematical world.)
One can already see this with one of the most basic conclusions of the “no self-defeating object” argument, namely that the set of natural numbers is infinite. Let me rephrase this result in the following manner:
Proposition 1. Let
be a set of natural numbers with the following properties:
lies in
.
- Whenever a natural number
lies in
, then its successor
also lies in
.
Then
is infinite.
Indeed, from the principle of mathematical induction, the hypotheses of Proposition 1 force to be the entire set of natural numbers, and so Proposition 1 is logically equivalent to the assertion that the set of natural numbers is infinite. (Here, infinite has its usual set theoretic meaning, i.e. the conclusion is that
cannot be placed in bijection with a set of the form
for any natural number
.)
In the rigorous world of formal mathematics, Proposition 1 is of course uncontroversial, and is easily proven by a simple “no self-defeating object” argument:
Proof. Suppose for contradiction that was finite. As
is non-empty (it contains
), it must therefore have a largest element
(as can be seen by a routine induction on the cardinality of
). But then by hypothesis,
would also have to lie in
, and
would thus need to be at least as large as
, a contradiction.
But if one allows for vagueness in how one specifies the set , then Proposition 1 can seem to be false, as observed by the ancient Greeks with the sorites paradox. To use their original example, consider the question of how many grains of sand are required to make a heap of sand. One or zero grains of sand are certainly not sufficient, but clearly if one places enough grains of sand together, one would make a heap. If one then “defines”
to be the set of all natural numbers
such that
grains of sand are not sufficient to make a heap, then it is intuitively plausible that
obeys both Hypothesis 1 and Hypothesis 2 of the above proposition, since it is intuitively clear that adding a single grain of sand to a non-heap cannot convert it to a heap. On the other hand, it is just as clear that the set
is finite, thus providing a counterexample to Proposition 1.
The problem here is the vagueness inherent in the notion of a “heap”. Given a pile of sand , the question “Is
a heap?” does not have an absolute truth value; what may seem like a heap to one observer may not be so to another. Furthermore, what may seem like a heap to one observer when presented in one context, may not look like a heap to the same observer when presented in another context; for instance, a large pile of sand that was slowly accumulated over time may not seem as large as a pile of sand that suddenly appeared in front of the observer, even if both piles of sand were of identical size in absolute terms. (The well-known (though technically inaccurate) boiling frog metaphor is a particularly graphic way of depicting this phenomenon, which ultimately arises from the fact that people usually do not judge quantities in absolute terms, but instead by using relative measurements that compare that quantity to nearby reference quantities.)
There are many modern variants of the sorites paradox that exploit vagueness of definition to obtain conclusions that apparently contradict rigorous statements such as Proposition 1. One of them is the interesting number paradox. Let be the set of all natural numbers that are “interesting”, in the sense that they have some unusual defining feature (for instance, 561 is the first composite Carmichael number and is thus presumably an interesting number). Then
is presumably finite, but the first natural number that does not lie in
is presumably also an interesting number, thus contradicting the definition of
. (Here, the variant of Proposition 1 that is apparently being contradicted here is the well-ordering principle.)
Of course, just as the sorites paradox can be diagnosed as arising from the vagueness of the term “heap”, the interesting number paradox can be diagnosed as arising from the vagueness of the term “interesting”. But one can create a functionally similar paradox that, at first glance, eliminates this vagueness, namely the Berry paradox. Let denote the set of all natural numbers that can be defined in fewer than sixteen words in the English language; thus, again 561 can be defined as “The first composite Carmichael number” and thus belongs in
. As there are only finitely many sentences that one can form with fewer than sixteen words of the English language,
is clearly finite. But the first natural number that does not lie in
can be described as “The first natural number not definable in fewer than sixteen words in the English language”, which is a definition in fewer than sixteen words in the English language, and thus lies in
, again providing another seeming contradiction to the well-ordering principle.
Here, the vagueness is a bit harder to spot, and it comes from the use of “the English language”, which is a vague and mutable concept that allows for self-reference and is in fact technically inconsistent if one tries to interpret it naively (as can be seen from any number of linguistic paradoxes, starting with the classic liar paradox). To make things more precise, one can try to replace the English language here by a formal mathematical language, e.g. the language of true arithmetic. Let us take one such formal language and call it . Then one can certainly define the set
of all natural numbers that can be definable in fewer than sixteen words in the language
, and one can form the natural number
, defined as “The first natural number not definable in fewer than sixteen words in the language L”. This is a natural number that is definable in fewer than sixteen words – but not in the language
, but rather in a meta-language
that, among other things, is able to interpret what it means for a sentence in
to define a natural number. This requires a truth predicate for
, and Tarski’s indefinability theorem asserts that such a predicate cannot exist inside
itself. Indeed, one can interpret Berry’s paradox as providing a proof of Tarski’s theorem. Thus we see that a non-trivial mathematical theorem (in this case, Tarski’s theorem) emerges when one finally clears away all the vagueness from a sorites-type paradox. (If instead one replaced the word “definable” by “provably definable”, and used a formal axiom system
as one’s language, one could similarly deduce Gödel’s incompleteness theorem from this argument.)
Similar paradoxes come up when trying to enumerate the real numbers, or subsets of real numbers. Here, the analogue of Proposition 1 is
Proposition 2. Let
be a set of real numbers with the following properties:
is infinite.
- Given any sequence
of elements of
, one can find another element
of
that is not equal to any of the elements of the sequence (i.e.
for every positive integer
).
Then
is uncountable.
(Of course, uncountability has the usual set-theoretic definition, namely that the infinite set is not in one-to-one correspondence with the natural numbers.)
Again, in the rigorous world in which all terms are clearly defined, this proposition is easily proven:
Proof. Suppose for sake of contradiction that was countable. Then, being infinite, it could be enumerated by a sequence
of real numbers in
; but then by hypothesis #2, there would then be another real number
that was also in
, but distinct from all of the elements of the sequence, contradicting the fact that this was an enumeration.
Since Cantor’s diagonal argument demonstrates that the set of reals itself obeys hypothesis #2 (and also clearly obeys hypothesis #1), we conclude as a corollary that the reals are uncountable.
However, one can find apparent counterexamples to Proposition 2 if one deploys enough vagueness. For instance, in the spirit of the Berry paradox, one could try setting to be the set of all “definable” real numbers – those numbers that can be defined using a finite sentence in the English language. As there are only countably many such sentences,
would be countable; it is also clearly infinite. But, on the other hand, one could take any sequence of real numbers
in
and apply the diagonal argument to define another real number that does not lie in that sequence.
Again, this apparent contradiction becomes clarified if one removes the vagueness, by replacing “the English language” with a formal language . For instance, one could take
to be true arithmetic, and
to be the set of all real numbers that are definable by a sentence in
. Then
is indeed countable, but any enumeration of
requires the truth predicate for
and thus such an enumeration (as well as the Cantor diagonalisation thereof) cannot be defined in
, but only in a meta-language
– thus obtaining yet another proof of Tarski’s indefinability theorem. Or, one could take
to be a programming language, such as the language of Turing machines; then again the set
of real numbers whose decimal expansion can be given as the output of an algorithm in
is countable, but to enumerate it one would have to solve the halting problem for
, which requires a meta-language
that is distinct from
itself; thus in this case the diagonalisation argument gives a proof of Turing’s halting theorem.
It is also instructive to contrast the formal distinction between countable and uncountable sets with the sorites paradox distinction between a non-heap and a heap of sand. Intuitively, the act of adding one grain of sand to a non-heap cannot directly turn that non-heap into a heap, and yet Proposition 1 forces this to eventually be the case. Similarly, it is intuitively clear that act of producing a single real number not on one’s countable enumeration of a set does not directly convert a countable set to become uncountable, and yet Proposition 2 forces this to eventually be the case. (More formally, Proposition 1 is powered by the principle of mathematical induction, which allows one to iterate the
operation indefinitely (or more precisely, up to the first infinite ordinal
) to explicitly achieve infinite cardinality; in a similar spirit, one can interpret Proposition 2 as being powered by transfinite induction, in the sense that one can iterate the diagonalisation operation indefinitely (or more precisely, up to the first uncountable ordinal
) to explicitly achieve uncountable cardinality. The transition from countability to uncountability does not occur during the successor ordinal steps of this transfinite induction, but during the (final) limit ordinal step.)
One can perform a similar analysis for the other results discussed previously in this series. For instance, Russell’s paradox tells us, among other things, that (assuming the standard Zermelo-Frankel axioms of set theory) the class of all sets cannot itself be a set. Actually we have the following slightly more general statement, analogous to Proposition 1 or Proposition 2:
Proposition 3. Let
be a class of sets with the following properties:
- The empty set
belongs to
.
- If a set
belongs to
, then the singleton set
also belongs to
.
- If any collection
of sets
, indexed by another set
, is such that each
lies in
, then their union
also lies in
.
Then
is not a set.
(Hypothesis #1 is actually redundant, being implied by the trivial case of Hypothesis #3 when is empty, but we keep it in order to emphasise the similarity with Propositions 1 and 2.) The Zermelo-Frankel axioms (as well as one’s intuition from naive set theory) tell us that the class of all sets obeys Hypotheses #1, #2, #3, and so cannot be a set. (In fact, the above proposition is essentially equivalent to the slightly stronger assertion that the class of all well-founded sets, also known as the von Neumann universe
, is not a set.) A key subtlety is that the set
itself is not required to lie in
. If one imposes such a restriction, then
can become a set (and by adding a few additional axioms, such sets become the same concept as Grothendieck universes).
Proof. Suppose for contradiction that is a set. Using the axiom (schema) of specification, the set
is then a set. It is the union of all the singleton sets
with
, so by Hypotheses #2 and #3,
. But then we see that
if and only if
, which is absurd.
Again, the hypotheses in this proposition seem innocuous, much like adding a single grain of sand to a non-heap of sand; but if one iterates them indefinitely then one eventually ends up with a class so large that it is no longer a set. (Here, the transfinite induction is not up to the first infinite ordinal or the first uncountable ordinal, but rather across the class of all ordinals; the point then being that the class of all ordinals is itself not a set.) Naive set theory intuition seems to be in contradiction to Proposition 3, but this is only due to the vagueness inherent in that concept of set theory. One can also try analysing Berry-type paradoxes in this setting, for instance working only with “constructible” sets (i.e. elements of Gödel’s universe ); the consequence one gets from this is that the class of constructible sets is not itself constructible (in fact, it is not even a set, as it contains all the ordinals).
Proposition 3 may seem only of interest to set theorists and logicians, but if one makes a tiny modification of it, by replacing a class of sets with a partially ordered class, then one gets a very important result:
Lemma 4. (Zorn’s lemma) Let
be a partially ordered class which obeys the following properties:
- At least one element belongs to
.
- If
is an element of
, then there is another element
of
such that
.
- If
is a totally ordered set in
, indexed by another set
, then there exists an element
such that
for all
.
Then
is not a set.
This lemma (which, of course, requires the axiom of choice to prove, and is in fact equivalent to this axiom) is usually phrased in the contrapositive form: any non-empty set for which every totally ordered set has an upper bound, has a maximal element. However when phrased in the above form, we see the close similarity between Zorn’s lemma and Propositions 1, 2, and 3. In this form, it can be used to demonstrate that many standard classes (e.g. the class of vector spaces, the class of groups, the class of ordinals, etc.) are not sets, despite the fact that each of the hypotheses in the lemma do not directly seem to take one from being a set to not being a set. This is only an apparent contradiction if one’s notion of sets is vague enough to accommodate sorites-type paradoxes.
More generally, many of the objects demonstrated to be impossible in the previous posts in this series can appear possible as long as there is enough vagueness. For instance, one can certainly imagine an omnipotent being provided that there is enough vagueness in the concept of what “omnipotence” means; but if one tries to nail this concept down precisely, one gets hit by the omnipotence paradox. Similarly, one can imagine a foolproof strategy for beating the stock market (or some other zero sum game), as long as the strategy is vague enough that one cannot analyse what happens when that strategy ends up being used against itself. Or, one can imagine the possibility of time travel as long as it is left vague what would happen if one tried to trigger the grandfather paradox. And so forth. The “self-defeating” aspect of these impossibility results relies heavily on precision and definiteness, which is why they can seem so strange from the perspective of vague intuition.

32 comments
Comments feed for this article
3 November, 2010 at 1:20 am
gowers
I’m not sure I understand the point you are making just after you state Proposition 1, since in the proof you use the fact that a finite set of positive integers has a maximum, which, it seems to me, needs induction for its proof. Of course, it’s inevitable that you will use something of the same strength as induction to prove something of (pretty much) the same strength as induction. Are you treating the well-ordering principle as somehow more basic than induction in its usual form?
I’m writing this without having got to the end of the post. This is just a minor quibble — I’m enjoying the main point about vagueness.
3 November, 2010 at 7:39 am
Terence Tao
I guess I am splitting Proposition 1 into two pieces:
Proposition 1a: If the set of natural numbers obeys Hypotheses 1 and 2, then it is the entire set of natural numbers.
of natural numbers obeys Hypotheses 1 and 2, then it is the entire set of natural numbers.
Proposition 1b: The natural numbers are infinite.
Proposition 1a is precisely the principle of mathematical induction. Proposition 1b, as you note, is a fairly short consequence of mathematical induction (which one needs to prove Sublemma 1′: every finite set has a maximal element), but I consider it slightly ‘harder’ than mathematical induction (for instance, it requires the total ordering of the natural numbers, which actually takes a non-trivial amount of effort to prove if one is starting from the Peano axioms, and also the proof has to go via contradiction or negation). So, from a relative perspective, Proposition 1 and Proposition 1b are equivalent modulo induction (but both are fairly easy to show with induction, so this is not a very strong assertion). I’ve reworded the text slightly to emphasise this point.
Proposition 1 is of course very close in spirit to the well-ordering principle too, but technically I would consider it a different result; the well-ordering principle does not directly say anything about the cardinality of the natural numbers without a fair amount of additional argument.
3 November, 2010 at 4:13 am
Jack
“In the rigorous world of formal mathematics, Proposition 1 is of course uncontroversial, and is easily proven…”
But isn’t Prop. 1 the definition of the natural numbers (once you add closure: only what is derivable from 1 by finite application of 2…)? If you accept recursive definition of the natural numbers, then the proposition is trivial, but if someone is uncertain of how to formalize the usual `definition’ N={0,1,2,..}, they will be uncertain of the proof.
3 November, 2010 at 7:46 am
Terence Tao
But isn’t Prop. 1 the definition of the natural numbers?
No, this is what I call Proposition 1a in my reply to Tim Gowers. Proposition 1 actually does not need the notion of the set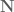 of natural numbers, and can be stated and proved merely knowing that the natural numbers form a class rather than a set (i.e. one still has the predicate “
of natural numbers, and can be stated and proved merely knowing that the natural numbers form a class rather than a set (i.e. one still has the predicate “ is a natural number”, but one does not have a notion of the set of natural numbers).
is a natural number”, but one does not have a notion of the set of natural numbers).
One can phrase Proposition 1 in the contrapositive, so that it becomes a result in finite set theory (set theory without the axiom of infinity): if is a finite set of natural numbers, then either
is a finite set of natural numbers, then either  does not contain 0, or else there is a natural number
does not contain 0, or else there is a natural number  in
in  such that
such that 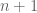 does not lie in
does not lie in  . This statement, and its proof, does not require any infinite sets at all, though of course it still does use the principle of mathematical induction (it is hard to do much at all with the natural numbers without this principle).
. This statement, and its proof, does not require any infinite sets at all, though of course it still does use the principle of mathematical induction (it is hard to do much at all with the natural numbers without this principle).
3 November, 2010 at 5:58 am
John Sidles
When proving theorems about (for example) prime numbers, I am not troubled by feelings of vagueness, because given an integer asserted to be prime, I can concretely verify that it is prime.
But when proving theorems about (for example) the complexity class P, doubts assail me, because given an algorithm asserted to be in P, there is no general means to verify that it is in P … membership is decided instead by a (never-instantiated) oracle.
This “oracular” vagueness is (AFAICT) a peculiar and distinctive feature of complexity theory, that even the completeness theorems do not share.
How commonly does it occur, that students are troubled by the oracular vagueness that is associated to complexity theory?
Is there a (gentle) textbook that discusses oracular vagueness in general, and in particular the oracular vagueness of deciding membership in P (and thus, membership in NP too)?
3 November, 2010 at 8:49 am
Terence Tao
This is part of the more general point (made in this post) that in order to completely describe any formal mathematical language L, one needs to use a meta-language L’ that is more expressive than L itself, as the ability of a language L to properly reference itself would be self-defeating. So if one is doing any analysis of systems, one needs a hierarchy of at least two languages, an “internal” language that describes things that are “observable”, “computable”, or “provable” inside the system, and an “external” language that completely describes the external interpretation of that system. This external language could in turn be completely formalised and analysed from an even more external viewpoint, but only by working in a yet more expressive language… and so, given that our human reasoning capacity is finite, one must eventually stop at an outermost layer of language that is either (a) informal or otherwise vague, (b) unable to be externally analysed, (c) unable to prove its own consistency, (d) inconsistent, or (e) too weak to do any serious mathematics. But we can at least insulate all of our mathematical reasoning from this outermost layer by working in a formal internal system inside the informal or indescribable external one (and one which can be nested arbitrarily deeply in this hierarchy). In particular, one can push the vagueness in one’s reasoning to a different layer from the layer in which one is doing mathematics.
In the more specific case of polynomial time algorithms, one can certainly encode the concept of P (and more generally, to externally analyse polynomial time algorithms) inside a more expressive theory, such as set theory with the axiom of infinity, or by using infinite time algorithms. (I touch upon this latter point in this post of mine.) Now, of course, to be able to externally analyse those latter concepts completely, one would need an even more expressive theory, but in practice one does not need to go arbitrarily high up this hierarchy in order to actually get some mathematics done.
In any event, just about any subject of study in mathematics (or theoretical computer science) can be described externally using set theory (and usually ZFC is more than sufficient), so one can argue that the problem of vagueness can be delegated to the set theorists (and, moving up the externality hierarchy, to the logicians and then to the philosophers) to resolve.
7 November, 2010 at 4:32 pm
John Sidles
Prof. Tao, thank you for this terrific answer, which went far toward clarifying my understanding of the role of oracles in defining complexity classes in general, and the classes P and NP in particular.
For me—and I think for many people—the contemplation of concrete examples does much to mitigate feelings of vagueness. Thus, it has greatly helped my understanding of proof theory that Gödel exhibited concrete examples of undecidable formulas. Similarly, it would help my understanding of complexity theory if concrete examples were exibited of algorithms in P for which membership in P similarly was undecidable.
On Scott Aaronson’s blog Shtetl Optimized, Kaveh Khodjasteh took the trouble to discuss these decidability-in-complexity issues in some depth (including good references).
Thanks to posts like yours and Kevah’s, it is feasible for a student and/or non-expert to begin with an understanding at the level of (say) Nagel and Newman’s Gödel’s Proof, then work her way through your post, Kevah’s post, and then the in-depth discussion of Krajicek and/or Cook and Nguyen (as referenced by Kaveh) … with at least some hope of emerging with a working understanding of the central roles that decidability and oracles play in defining complexity classes.
It is definitely *not* the case that I have myself gained this understanding … in aggregate, these references are lengthy and plenty tough. But I *have* learned the value of vigorous weblogs in making these mathematical ideas accessible to non-experts. For which, this post is an expression of appreciation and thanks.
8 November, 2010 at 8:25 am
John Sidles
PS: as I wade deeper into MathOverflow and TCS StackExchange, I find there are at least two persons who post as “Kaveh” on these forums, namely Kaveh Ghasemloo (mainly on MathOverflow) and Kaveh Khodjasteh (mainly on TCS StackExchange) … and perhaps there are even more “Kavehs” than this.
So in respect to the question “How big is P?”, my thanks and appreciation should have been extended more broadly, to encompass everyone who has posted under the name “Kaveh”.
3 November, 2010 at 3:49 pm
David Milovich
Godel’s L can’t be a set, at least not in ZF, because L contains as a definable subclass the von Neumann ordinals ordinals On, i.e., the class of all transitive sets strictly well ordered by the membership relation. But by the Burali-Forti paradox, ZF proves that On is not a set, so, by the Axiom of Specification, neither is L a set.
Actually, not all of ZF is required for the above argument: the axioms of Infinity, Replacement, and Foundation are certainly not used in the proof of Burali-Forti from Chapter 1 of Kunen’s book, nor is anything remotely close to the full strength of the Power Set Axiom used. (I strongly suspect coding could eliminate the use of the Power Set Axiom entirely, though at the expense of assuming the Axiom of Infinity.)
[Ah, corrected, thanks. I got confused because one can cut off L at a suitably large cardinal to make internal models of set theory, but L itself does not qualify for this purpose. -T.]
3 November, 2010 at 10:44 pm
Ted Gast
Another paradox related to uncountable sets is Skolem’s Paradox. By the Lowenheim-Skolem theorem any countable first order theory with an infinite model must have a countable model. ZFC has a countable first order formulation, thus assuming ZFC has a model (which must be infinite because it satisfies the axiom of infinity), ZFC has a countable model, call it M. But this is an apparent paradox, because M must presumably contain the powerset of the natural numbers, an uncountable set. The way around this paradox is to realize that M may not contain the actual powerset of the natural numbers, just a countable set P, that M thinks is the powerset. Further Cantor’s diagonal argument shows that the bijection of P with the natural numbers, is not in M. This paradox can be disconcerting as it suggests that a set being uncountable is a relative, rather than absolute notion.
4 November, 2010 at 1:18 am
Uwe Stroinski
Consider terms like ‘square root of 2’, ‘square root of -1’ or ‘non-Euclidean geometry’. All of them were once known to not exist and later being constructed (albeit in larger sets). They are now part of our syllabus.
What do you think, is it farfetched to believe that ‘the self-defeating object’ has a similar fate? It ‘contradicts’ the law of excluded middle and thus the two-valuedness of our logic. Due to its circularity it also doesn’t fit well into our ‘bottom-up’ framework of constructing objects. Is it impossible that someday someone will start with ‘the set of all sets’ and construct mathematics ‘top-down’ in terms of some many-valued logic not obeying the law of excluded middle? The result would be mind-boggling (as were the imaginary numbers at their time) and in a way a justification for people feeling ‘uneasy’ about the above proof method.
4 November, 2010 at 6:14 am
Roger Witte
There are set theories that admit the set of all sets with classical logic and the excluded middle. There is Quine’s NF/NFU family of theories (see Randall Holmes wb pages) and there are Positive set theories (which originate in topology).
Actually in the main candidate for alternative logics for mathematics, intuitionist logic and constructive mathematics, the self-defeating object causes less uneasiness because there are many thing that neither are or are not.
Similarly, some category theorists postulate that the problems arise because standard set theory allows questions that should be ill-formed to be meaningful. For example is the empty set a member of the complex number e? They use theories like Lawvere’s Elementary Theory of The Category of Sets in which sets and their members are of different types.
I have also heard of attempts at ‘inconsistent mathematics’ and ‘paraconsistent logic’, which attempt to allow P and not P without collapse into triviality but I don’t know much about them.
6 November, 2010 at 8:37 am
anon
To summarize classical logic asserts the 3 classical principles or laws of thought: identity, no-contradiction and excluded middle. Deviant logics (Susan Haack), such as minimal logics, intuitionism or paraconsistent logics (which is more a family of logics than a single logic) are variants which does not accept some of these principles. Quantum logic can also be seen as a deviant logic which differs from classical regarding the distributiveness.
And in fact, an apparently paradoxical fact, with any of these deviant logics (i do not know if this is the case also for quantum logic) you can do less than with classical (the set of valid inferences is weaker), the reason beeing explained bellow by Prof Tao (Wikipedia articles are a also a good reference to start with). I suggest also the paper from Béziau “S5 is a paraconsistent logic and so is first order classical logic”.
Universal logic is a brand new trend in logic which tries to integrate all these “deviant” and other new logics (multivalued…), in a common frame.
Under this frame i suppose they are not seeing as deviant anymore, just possible logics as non-euclidean geometries are possible geometries.
Regarding multivaluedness Suszko thesis is a good start: http://plato.stanford.edu/entries/truth-values/supplement1.html.
4 November, 2010 at 8:52 am
Terence Tao
Well, as your examples show, one can certainly add an overpowered object to one’s system as long as one depowers something else. For instance, one can add the square root of -1 to one’s number system as long as one depowers the order operation <; one can consider non-Euclidean geometries if one depowers the parallel postulate; and so forth. With regard to, say, "the set of all sets", there is for instance New Foundations (mentioned in another comment), which admits this set, but only by depowering the concept of a function (so, in particular, the singleton-forming map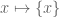 is not considered to be a function from any set
is not considered to be a function from any set  to the set of its singletons). And if one depowers the notion of a definite, two-valued truth value to every mathematical statement, then certainly many previously impossible things become possible (or at least not impossible).
to the set of its singletons). And if one depowers the notion of a definite, two-valued truth value to every mathematical statement, then certainly many previously impossible things become possible (or at least not impossible).
But the real test is whether these extended systems of mathematics actually make it easier for one to say anything new about the "core" systems of mathematics (e.g. the natural numbers). The complex numbers, for instance, have been spectacularly successful in this regard, whereas the quaternion numbers, which are superficially a similar type of extension to the real numbers (and arguably "better", as it allows for more objects than the complex numbers) have not. The problem here is that the quaternion numbers depowered far too much (in particular, depowering the commutativity of multiplication, which made the polynomial ring much nastier) for the addition of the new objects to be particularly worthwhile.
From a foundational perspective, the impossibility arguments given in this series of posts can be viewed as a road map that gives a list of items that one must select from to depower in order to enable a self-defeating object to exist. (For instance, definiteness of truth is certainly one of the options to depower here, which is why self-defeating objects are much more plausible in vague models of mathematics than in definite ones.) But the cost of this depowering to one's ability to do mathematics is so great that there must be some significant other advantage, beyond the ability to introduce the self-defeating objects, to make the transition. (The complex numbers form a good example again; if all they allowed one to do is take the square root of -1, they would be next to useless. It is only because they happen to offer so much more – an algebraically complete field structure, an elliptic conformal geometry, etc. – that they are so indispensable in modern mathematics.)
6 November, 2010 at 7:40 am
gelada
In terms of depowering “definiteness of truth”, I think it is worth analysing how deep the losses are. For example in his discussion of what we could do it the axioms of arithmetic are inconsistent: http://video.ias.edu/voevodsky-80th Vladimir Voevodsky considers systems where every statement contains its proof steps from the axioms. In this case contradiction is depowered as it no longer causes the whole system to fail.
In this case the advantage: being able to continue doing mathematics, is obvious. It would be interesting to know the exact costs. For example within these systems can one avoid the esoteric details of non-standard analysis?
4 November, 2010 at 6:02 am
Roger Witte
“Let A be the set of all natural numbers that are “interesting”, in the sense that they have some unusual defining feature (for instance, 561 is the first composite Carmichael number and is thus presumably an interesting number). Then A is presumably finite”
On reading this fragment my first thought was “prime numbers are interesting” and “There is no largest Prime” therefore “A is infinite”.
(Actually this makes it a good example of vagueness, since you and I immediately jumped to opposite conclusions from the same description).
4 November, 2010 at 8:55 am
Terence Tao
One has to be careful here to avoid a fallacy of distribution. The set of prime numbers is certainly interesting; but this does not imply that each individual prime number is itself interesting.
4 November, 2010 at 7:47 am
Pace Nielsen
I thought I’d try to use your ideas in the last post on this subject, to give my students an introduction to uncountable sets, without entering a counter-factual world. I think it went over pretty well.
There was one further point of confusion expressed by a few students. It related to timing, which ultimately boils down to the fact that quantifiers do not commute. They were initially confused by the fact that we are *given* a countable list r_1, r_2,… and using this list we can construct something not in the list. They asked why we couldn’t use the element we constructed to modify our list at the time. So, if you are trying to delve into what confuses students, I would just add “non-commutativity of quantifiers”.
6 November, 2010 at 7:07 am
Robert Coulter
There are practical scenarios here that I believe mathematicians should do more research. For example, engineering models often give some statement indicating the “accuracy” of the models. These accuracy statements are often of the form:
“Model error is greater than 5 % if p > pmax” (e.g.).
So why bother with the accuracy statement? If the model “knows” there is an error approaching pmax, why doesn’t it incorporate an error correction term to account for it? Then move the accuracy statement out to a further bound, say at a new pmax1. But then there would have to be some point where the model knows nothing and no accuracy statement can be given. Are we better off in that case? It seems as though, from an engineering standpoint, that a model with a “flaw” and an accuracy statement is superior to a model with “flaw correction” and no accuracy statement.. In other words, a model, no matter how accurate, is consider inferior if it cannot say anything about its own accuracy.
14 November, 2010 at 4:15 pm
John Mangual
Our intuition may fail in these cases b/c math is a discipline where every statement has to be ascribed a truth value “true” or “false”. Outside of mathematics this binary classification may be a bit simplistic. In other fields (even quantitative) it may not be possible to resolve every statement into one of these two categories. (Upon closer reading, you’ve already mentioned this.)
Also, maybe a collection of grains of sand becomes a heap when we’re no longer able to count. It takes a certain amount of energy and resources to count every single grain of sand. After a certain point, one might just give up and eat a sandwich.
15 November, 2010 at 9:47 am
Robert Coulter
A heap of sand is just a heap of sand until it is noted that it consists of individual grains, and then logic can be deployed to destroy the definition. Yet somehow the usefulness of the definition still exists.
I also find it interesting that the generally accepted to view of deep reality is that is obeys a form of logic (or illogic) that basically states that there is no deep reality:
http://en.wikipedia.org/wiki/Bell's_theorem
27 November, 2010 at 12:42 am
Mathematics and realism « Xi'an's Og
[…] necessarily stem from the human mind and from human perceptions. (He paradoxically quotes Gödel to back his point, while Gödel actually was in agreement with Platonicism.) He then diverges […]
29 November, 2010 at 12:18 am
Aru Ronelect
Dear Terens Tao,
Thanks for a surprisingly fresh post on global “mathematical” ideas. Looks like common sense is not yet dead in math :))))
You talk about vagueness, as a solution for many paradoxes. I think these things belong to the domain of metalanguage as you call it. I would rather say metaprogramming language, or even better metaphysics – so hated word these days :))). Since thinking and your previous post is some sort of programm-calculation.
What you call mathematics is a very small set (though very important for many reasons) of this metaphysicall programm language, lets call is human mind later on for simplicity.
If we look at what you said from this perspective we see that paradoxes (in their naive form) are impossible. Since paradox is just a type of calculation, type of statement (usually about infinity, in a form of recursion), or if you want just a message.
From here we see that vagueness as you call it, is not something from outside, its actually one of the core elements of this metaprogramming language (mind, thinking, feeling), acutally quite vice versa mathematics is some sort of paradox in this realm since it sometimes gives a feeling of absolute predictablilty, which is obviously not there.
So here with vagueness you go back to the roots, to the original conceptual language used in our heads. Moreover in your first theorem about natural numbers its obvious that you assume we understand what a number is. But we dont. And nobody does. Because number is exactly one of the main blocks of this metalanguage.
And even idea of recursion and infinity is not something you (we humans) come up with, its also a corestone block of this language.
So to sum up. From your post its obvious that you as a person is in the possession of the very complex highly conceptual (means rich) language. Well, actually language is already a set of conceptions including the conception of set :)))
29 November, 2010 at 1:03 am
Aru Ronelect
I got into thinking about this. Have to add something :)
Paradoxes and dualism are everywhere. Better to say calculation errors (expectationsVSresult). So if we look at human mind and universe as a program (for first simplicity) we see that paradox-error is most fundamental element of program work. No errors – no development. Well, there is development without error but this is just traveling.
It also seems obvious that its impossible to get rid from binary logic of true-false at fundamental level since its just reformulates obvious fact about if something exist or not exist there is nothing in between.
19 December, 2010 at 2:42 pm
Dangerous Knowledge « /Users/dan/proj
[…] I just wanted to add a link to an awesome post by Terrence Tao about the kind of paradoxes I’ve summarized here. Visit and subscribe to his blog, for it is […]
19 February, 2011 at 9:53 am
Finite Sets | Poincare's Paradise
[…] links are link1,link2,link3. By going through these links we can understand how this method has been used in mathematics, […]
21 July, 2011 at 1:53 am
Alexander Kruel · GiveWell, the SIAI and risks from AI
[…] most of this superficial simplicity is a result of the vagueness of natural language descriptions. Reducing the vagueness of those concepts by being more specific, or by coming up with technical definitions of each of the […]
20 May, 2012 at 2:59 pm
Heuristic limitations of the circle method « What’s new
[…] (in the spirit of “self-defeating object” arguments, discussed previously several times on this blog). This is actually a fairly common technique in analytic number theory (though not usually […]
3 November, 2012 at 3:14 am
Alexander Kruel · What I would like the Singularity Institute to publish
[…] [41] The “no self-defeating object” argument, and the vagueness paradox […]
16 January, 2019 at 8:43 am
245A: Problem solving strategies | What's new
[…] objects one is applying Zorn’s lemma to is actually a set rather than a proper class; see this previous blog post for more […]
16 December, 2019 at 2:44 am
.
Is there a self defeating when you deal with things that are ‘finite’?
15 May, 2020 at 2:02 am
Michael Stone
Dear Mr. Tao,
This post brought me some comfort on a sleepless night thinking about the axiom of choice and the well ordering principal. Thank you.