245A, Notes 6: Outer measures, pre-measures, and product measures

30 October, 2010 in 245A - Real analysis, math.CA, math.PR | Tags: Caratheodory extension theorem, Hahn-Kolmogorov extension theorem, Kolmogorov extension theorem, outer measure, product measure | by Terence Tao

In this course so far, we have focused primarily on one specific example of a countably additive measure, namely Lebesgue measure. This measure was constructed from a more primitive concept of Lebesgue outer measure, which in turn was constructed from the even more primitive concept of elementary measure.
It turns out that both of these constructions can be abstracted. In this set of notes, we will give the Carathéodory lemma, which constructs a countably additive measure from any abstract outer measure; this generalises the construction of Lebesgue measure from Lebesgue outer measure. One can in turn construct outer measures from another concept known as a pre-measure, of which elementary measure is a typical example.
With these tools, one can start constructing many more measures, such as Lebesgue-Stieltjes measures, product measures, and Hausdorff measures. With a little more effort, one can also establish the Kolmogorov extension theorem, which allows one to construct a variety of measures on infinite-dimensional spaces, and is of particular importance in the foundations of probability theory, as it allows one to set up probability spaces associated to both discrete and continuous random processes, even if they have infinite length.
The most important result about product measure, beyond the fact that it exists, is that one can use it to evaluate iterated integrals, and to interchange their order, provided that the integrand is either unsigned or absolutely integrable. This fact is known as the Fubini-Tonelli theorem, and is an absolutely indispensable tool for computing integrals, and for deducing higher-dimensional results from lower-dimensional ones.
We remark that these notes omit a very important way to construct measures, namely the Riesz representation theorem, but we will defer discussion of this theorem to 245B.
This is the final set of notes in this sequence. If time permits, the course will then begin covering the 245B notes, starting with the material on signed measures and the Radon-Nikodym-Lebesgue theorem.

— 1. Outer measures and the Carathéodory extension theorem —

We begin with the abstract concept of an outer measure.

Definition 1 (Abstract outer measure) Let ${X}$ be a set. An abstract outer measure (or outer measure for short) is a map ${\mu^*: 2^X \rightarrow [0,+\infty]}$ that assigns an unsigned extended real number ${\mu^*(E) \in [0,+\infty]}$ to every set ${E \subset X}$ which obeys the following axioms:

(Empty set) ${\mu^*(\emptyset)=0}$ .

(Monotonicity) If ${E \subset F}$ , then ${\mu^*(E) \leq \mu^*(F)}$ .

(Countable subadditivity) If ${E_1, E_2, \ldots \subset X}$ is a countable sequence of subsets of ${X}$ , then ${\mu^* (\bigcup_{n=1}^\infty E_n) \leq \sum_{n=1}^\infty \mu^*(E_n)}$ .

Outer measures are also known as exterior measures.
Thus, for instance, Lebesgue outer measure ${m^*}$ is an outer measure (see Exercise 4 of Notes 1) is an outer measure. On the other hand, Jordan outer measure ${m^{*,(J)}}$ is only finitely subadditive rather than countably subadditive and thus is not, strictly speaking, an outer measure; for this reason this concept is often referred to as Jordan outer content rather than Jordan outer measure.
Note that outer measures are weaker than measures in that they are merely countably subadditive, rather than countably additive. On the other hand, they are able to measure all subsets of ${X}$ , whereas measures can only measure a ${\sigma}$ -algebra of measurable sets.
In Definition 1 of Notes 1, we used Lebesgue outer measure together with the notion of an open set to define the concept of Lebesgue measurability. This definition is not available in our more abstract setting, as we do not necessarily have the notion of an open set. An alternative definition of measurability was put forth in Exercise 17 of Notes 1, but this still required the notion of a box or an elementary set, which is still not available in this setting. Nevertheless, we can modify that definition to give an abstract definition of measurability:

Definition 2 (Carathéodory measurability) Let ${\mu^*}$ be an outer measure on a set ${X}$ . A set ${E \subset X}$ is said to be Carathéodory measurable with respect to ${\mu^*}$ if one has

$\displaystyle \mu^*(A) = \mu^*(A \cap E) + \mu^*(A \backslash E)$

for every set ${A \subset X}$ .

Exercise 3 (Null sets are Carathéodory measurable) Suppose that ${E}$ is a null set for an outer measure ${\mu^*}$ (i.e. ${\mu^*(E) = 0}$ ). Show that ${E}$ is Carathéodory measurable with respect to ${\mu^*}$ .

Exercise 4 (Compatibility with Lebesgue measurability) Show that a set ${E \subset {\bf R}^d}$ is Carathéodory measurable with respect to Lebesgue outer measure if and only if it is Lebesgue measurable. (Hint: one direction follows from Exercise 17 of Notes 1. For the other direction, first verify simple cases, such as when ${E}$ is a box, or when ${E}$ or ${A}$ are bounded.)

The construction of Lebesgue measure can then be abstracted as follows:

Theorem 5 (Carathéodory lemma) Let ${\mu^*: 2^X \rightarrow [0,+\infty]}$ be an outer measure on a set ${X}$ , let ${{\mathcal B}}$ be the collection of all subsets of ${X}$ that are Carathéodory measurable with respect to ${\mu^*}$ , and let ${\mu: {\mathcal B} \rightarrow [0,+\infty]}$ be the restriction of ${\mu^*}$ to ${{\mathcal B}}$ (thus ${\mu(E) := \mu^*(E)}$ whenever ${E \in {\mathcal B}}$ ). Then ${{\mathcal B}}$ is a ${\sigma}$ -algebra, and ${\mu}$ is a measure.

Proof: We begin with the ${\sigma}$ -algebra property. It is easy to see that the empty set lies in ${{\mathcal B}}$ , and that the complement of a set in ${{\mathcal B}}$ lies in ${{\mathcal B}}$ also. Next, we verify that ${{\mathcal B}}$ is closed under finite unions (which will make ${{\mathcal B}}$ a Boolean algebra). Let ${E, F \in {\mathcal B}}$ , and let ${A \subset X}$ be arbitrary. By definition, it suffices to show that

$\displaystyle \mu^*(A) = \mu^*( A \cap (E \cup F) ) + \mu^*( A \backslash (E \cup F) ). \ \ \ \ \ (1)$

To simplify the notation, we partition ${A}$ into the four disjoint sets

$\displaystyle A_{00} := A \backslash (E \cup F); \quad A_{10} := (A \backslash F) \cap E;$

$\displaystyle A_{01} := (A \backslash E) \cap F; \quad A_{11} := A \cap E \cap F$

(the reader may wish to draw a Venn diagram here to understand the nature of these sets). Thus (1) becomes

$\displaystyle \mu^*(A_{00} \cup A_{01} \cup A_{10} \cup A_{11}) = \mu^*(A_{01} \cup A_{10} \cup A_{11}) + \mu^*(A_{00}). \ \ \ \ \ (2)$

On the other hand, from the Carathéodory measurability of ${E}$ , one has

$\displaystyle \mu^*(A_{00} \cup A_{01} \cup A_{10} \cup A_{11}) = \mu^*(A_{00} \cup A_{01}) + \mu^*(A_{10} \cup A_{11})$

and

$\displaystyle \mu^*(A_{01} \cup A_{10} \cup A_{11}) = \mu^*(A_{01}) + \mu^*(A_{10} \cup A_{11})$

while from the Carathéodory measurability of ${F}$ one has

$\displaystyle \mu^*(A_{00} \cup A_{01}) = \mu^*(A_{00}) + \mu^*(A_{01});$

putting these identities together we obtain (2). (Note that no subtraction is employed here, and so the arguments still work when some sets have infinite outer measure.)
Now we verify that ${{\mathcal B}}$ is a ${\sigma}$ -algebra. As it is already a Boolean algebra, it suffices (see Exercise 6 below) to verify that ${{\mathcal B}}$ is closed with respect to countable disjoint unions. Thus, let ${E_1, E_2, \ldots}$ be a sequence of disjoint Carathéodory-measurable sets, and let ${A}$ be arbitrary. We wish to show that

$\displaystyle \mu^*(A) = \mu^*(A \cap \bigcup_{n=1}^\infty E_n) + \mu^*(A \backslash \bigcup_{n=1}^\infty E_n).$

In view of subadditivity, it suffices to show that

$\displaystyle \mu^*(A) \geq \mu^*(A \cap \bigcup_{n=1}^\infty E_n) + \mu^*(A \backslash \bigcup_{n=1}^\infty E_n).$

For any ${N \geq 1}$ , ${\bigcup_{n=1}^N E_n}$ is Carathéodory measurable (as ${{\mathcal B}}$ is a Boolean algebra), and so

$\displaystyle \mu^*(A) \geq \mu^*(A \cap \bigcup_{n=1}^N E_n) + \mu^*(A \backslash \bigcup_{n=1}^N E_n).$

By monotonicity, ${\mu^*(A \backslash \bigcup_{n=1}^N E_n) \geq \mu^*(A \backslash \bigcup_{n=1}^\infty E_n)}$ . Taking limits as ${N \rightarrow \infty}$ , it thus suffices to show that

$\displaystyle \mu^*(A \cap \bigcup_{n=1}^\infty E_n) \leq \lim_{N \rightarrow \infty} \mu^*(A \cap \bigcup_{n=1}^N E_n).$

But by the Carathéodory measurability of ${E_{N+1}}$ , we have

$\displaystyle \mu^*(A \cap \bigcup_{n=1}^{N+1} E_n) = \mu^*(A \cap \bigcup_{n=1}^N E_n) + \mu^*( A \cap E_{N+1})$

for any ${N \geq 0}$ , and thus on iteration

$\displaystyle \lim_{N \rightarrow \infty} \mu^*(A \cap \bigcup_{n=1}^N E_n) = \sum_{N=0}^\infty \mu^*( A \cap E_{N+1})$

On the other hand, from countable subadditivity one has

$\displaystyle \mu^*(A \cap \bigcup_{n=1}^\infty E_n) \leq \sum_{N=0}^\infty \mu^*( A \cap E_{N+1})$

and the claim follows.
Finally, we show that ${\mu}$ is a measure. It is clear that ${\mu(\emptyset)=0}$ , so it suffices to establish countable additivity, thus we need to show that

$\displaystyle \mu^*( \bigcup_{n=1}^\infty E_n ) = \sum_{n=1}^\infty \mu^*(E_n)$

whenever ${E_1,E_2,\ldots}$ are Carathéodory-measurable and disjoint. By subadditivity it suffices to show that

$\displaystyle \mu^*( \bigcup_{n=1}^\infty E_n ) \geq \sum_{n=1}^\infty \mu^*(E_n).$

By monotonicity it suffices to show that

$\displaystyle \mu^*( \bigcup_{n=1}^N E_n ) = \sum_{n=1}^N \mu^*(E_n)$

for any finite ${N}$ . But from the Carathéodory measurability of ${\bigcup_{n=1}^N E_n}$ one has

$\displaystyle \mu^*( \bigcup_{n=1}^{N+1} E_n ) = \mu^*( \bigcup_{n=1}^N E_n ) +\mu^*(E_{N+1})$

for any ${N \geq 0}$ , and the claim follows from induction. $\Box$

Exercise 6 Let ${{\mathcal B}}$ be a Boolean algebra on a set ${X}$ . Show that ${{\mathcal B}}$ is a ${\sigma}$ -algebra if and only if it is closed under countable disjoint unions, which means that ${\bigcup_{n=1}^\infty E_n \in {\mathcal B}}$ whenever ${E_1, E_2, E_3, \ldots \in {\mathcal B}}$ are a countable sequence of disjoint sets in ${{\mathcal B}}$ .

Remark 7 Note that the above theorem, combined with Exercise 4 gives a slightly alternate way to construct Lebesgue measure from Lebesgue outer measure than the construction given in Notes 1. This is arguably a more efficient way to proceed, but is also less geometrically intuitive than the approach taken in Notes 1.

Remark 8 From Exercise 3 we see that the measure ${\mu}$ constructed by the Carathéodory lemma is automatically complete, in the sense that any sub-null set for ${\mu}$ (a subset of a null set for ${\mu}$ ) is also a null set.

Remark 9 In 245C we will give an important example of a measure constructed by Carathéodory’s lemma, namely the ${d}$ -dimensional Hausdorff measure ${{\mathcal H}^d}$ on ${{\bf R}^n}$ that is good for measuring the size of ${d}$ -dimensional subsets of ${{\bf R}^n}$ .

— 2. Pre-measures —

In previous notes, we saw that finitely additive measures, such as elementary measure or Jordan measure, could be extended to a countably additive measure, namely Lebesgue measure. It is natural to ask whether this property is true in general. In other words, given a finitely additive measure ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ on a Boolean algebra ${{\mathcal B}_0}$ , is it possible to find a ${\sigma}$ -algebra ${{\mathcal B}}$ refining ${{\mathcal B}_0}$ , and a countably additive measure ${\mu: {\mathcal B} \rightarrow [0,+\infty]}$ that extends ${\mu_0}$ ?
There is an obvious necessary condition in order for ${\mu_0}$ to have a countably additive extension, namely that ${\mu_0}$ already has to be countably additive within ${{\mathcal B}_0}$ . More precisely, suppose that ${E_1, E_2, E_3, \ldots \in {\mathcal B}_0}$ were disjoint sets such that their union ${\bigcup_{n=1}^\infty E_n}$ was also in ${{\mathcal B}_0}$ . (Note that this latter property is not automatic as ${{\mathcal B}_0}$ is merely a Boolean algebra rather than a ${\sigma}$ -algebra.) Then, in order for ${\mu_0}$ to be extendible to a countably additive measure, it is clearly necessary that

$\displaystyle \mu_0( \bigcup_{n=1}^\infty E_n ) = \sum_{n=1}^\infty \mu_0(E_n).$

Using the Carathéodory lemma, we can show that this necessary condition is also sufficient. More precisely, we have

Definition 10 (Pre-measure) A pre-measure on a Boolean algebra ${{\mathcal B}_0}$ is a finitely additive measure ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ with the property that ${\mu_0( \bigcup_{n=1}^\infty E_n ) = \sum_{n=1}^\infty \mu_0(E_n)}$ whenever ${E_1,E_2,E_3,\ldots \in {\mathcal B}_0}$ are disjoint sets such that ${\bigcup_{n=1}^\infty E_n}$ is in ${{\mathcal B}_0}$ .

Exercise 11

Show that the requirement that ${\mu_0}$ is finitely additive could be relaxed to the condition that ${\mu_0(\emptyset)=0}$ without affecting the definition of a pre-measure.

Show that the condition ${\mu_0( \bigcup_{n=1}^\infty E_n ) = \sum_{n=1}^\infty \mu_0(E_n)}$ could be relaxed to ${\mu_0( \bigcup_{n=1}^\infty E_n ) \leq \sum_{n=1}^\infty \mu_0(E_n)}$ without affecting the definition of a pre-measure.

On the other hand, give an example to show that if one performs both of the above two relaxations at once, one starts admitting objects ${\mu_0}$ that are not pre-measures.

Exercise 12 Without using the theory of Lebesgue measure, show that elementary measure (on the elementary Boolean algebra) is a pre-measure. (Hint: use }{Lemma 6} from Notes 1. Note that one has to also deal with co-elementary sets as well as elementary sets in the elementary Boolean algebra.)

Exercise 13 Construct a finitely additive measure ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ that is not a pre-measure. (Hint: take ${X}$ to be the natural numbers, take ${{\mathcal B}_0 = 2^{\bf N}}$ to be the discrete algebra, and define ${\mu_0}$ separately for finite and infinite sets.)

Theorem 14 (Hahn-Kolmogorov theorem) Every pre-measure ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ on a Boolean algebra ${{\mathcal B}_0}$ in ${X}$ can be extended to a countably additive measure ${\mu: {\mathcal B} \rightarrow [0,+\infty]}$ .

Proof: We mimic the construction of Lebesgue measure from elementary measure. Namely, for any set ${E \subset X}$ , define the outer measure ${\mu^*(E)}$ of ${E}$ to be the quantity

$\displaystyle \mu^*(E) := \inf \{ \sum_{n=1}^\infty \mu_0(E_n): E \subset \bigcup_{n=1}^\infty E_n; E_n \in {\mathcal B}_0 \hbox{ for all } n \}.$

It is easy to verify (cf. Exercise 4 of Notes 1) that ${\mu^*}$ is indeed an outer measure. Let ${{\mathcal B}}$ be the collection of all sets ${E \subset X}$ that are Carathéodory measurable with respect to ${\mu^*}$ , and let ${\mu}$ be the restriction of ${\mu^*}$ to ${{\mathcal B}}$ . By the Carathéodory lemma, ${{\mathcal B}}$ is a ${\sigma}$ -algebra and ${\mu}$ is a countably additive measure.
It remains to show that ${{\mathcal B}}$ contains ${{\mathcal B}_0}$ and that ${\mu}$ extends ${\mu_0}$ . Thus, let ${E \in {\mathcal B}_0}$ ; we need to show that ${E}$ is Carathéodory measurable with respect to ${\mu^*}$ and that ${\mu^*(E) = \mu_0(E)}$ . To prove the first claim, let ${A \subset X}$ be arbitrary. We need to show that

$\displaystyle \mu^*(A) = \mu^*(A \cap E) + \mu^*(A \backslash E);$

by subadditivity, it suffices to show that

$\displaystyle \mu^*(A) \geq \mu^*(A \cap E) + \mu^*(A \backslash E).$

We may assume that ${\mu^*(A)}$ is finite, since the claim is trivial otherwise.
Fix ${\varepsilon > 0}$ . By definition of ${\mu^*}$ , one can find ${E_1,E_2,\ldots \in {\mathcal B}_0}$ covering ${A}$ such that

$\displaystyle \sum_{n=1}^\infty \mu_0(E_n) \leq \mu^*(A)+\varepsilon.$

The sets ${E_n \cap E}$ lie in ${{\mathcal B_0}}$ and cover ${A \cap E}$ and thus

$\displaystyle \mu^*(A \cap E) \leq \sum_{n=1}^\infty \mu_0(E_n \cap E).$

Similarly we have

$\displaystyle \mu^*(A \backslash E) \leq \sum_{n=1}^\infty \mu_0(E_n \backslash E).$

Meanwhile, from finite additivity we have

$\displaystyle \mu_0(E_n \cap E) + \mu_0(E_n \backslash E) = \mu_0(E_n).$

Combining all of these estimates, we obtain

$\displaystyle \mu^*(A \cap E) + \mu^*(A \backslash E) \leq \mu^*(A) + \varepsilon;$

since ${\varepsilon > 0}$ was arbitrary, the claim follows.
Finally, we have to show that ${\mu^*(E) = \mu_0(E)}$ . Since ${E}$ covers itself, we certainly have ${\mu^*(E) \leq \mu_0(E)}$ . To show the converse inequality, it suffices to show that

$\displaystyle \sum_{n=1}^\infty \mu_0(E_n) \geq \mu_0(E)$

whenever ${E_1,E_2,\ldots \in {\mathcal B}_0}$ cover ${E}$ . By replacing each ${E_n}$ with the smaller set ${E_n \backslash \bigcup_{m=1}^{n-1} E_m}$ (which still lies in ${{\mathcal B_0}}$ , and still covers ${E}$ ), we may assume without loss of generality (thanks to the monotonicity of ${\mu_0}$ ) that the ${E_n}$ are disjoint. Similarly, by replacing each ${E_n}$ with the smaller set ${E_n \cap E}$ we may assume without loss of generality that the union of the ${E_n}$ is exactly equal to ${E}$ . But then the claim follows from the hypothesis that ${\mu_0}$ is a pre-measure (and not merely a finitely additive measure). $\Box$
Let us call the measure ${\mu}$ constructed in the above proof the Hahn-Kolmogorov extension of the pre-measure ${\mu_0}$ . Thus, for instance, from Exercise 4, the Hahn-Kolmogorov extension of elementary measure (with the convention that co-elementary sets have infinite elementary measure) is Lebesgue measure. This is not quite the unique extension of ${\mu_0}$ to a countably additive measure, though. For instance, one could restrict Lebesgue measure to the Borel ${\sigma}$ -algebra, and this would still be a countably additive extension of elementary measure. However, the extension is unique within its own ${\sigma}$ -algebra:

Exercise 15 Let ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ be a pre-measure, let ${\mu: {\mathcal B} \rightarrow [0,+\infty]}$ be the Hahn-Kolmogorov extension of ${\mu_0}$ , and let ${\mu': {\mathcal B}' \rightarrow [0,+\infty]}$ be another countably additive extension of ${\mu_0}$ . Suppose also that ${\mu_0}$ is ${\sigma}$ -finite, which means that one can express the whole space ${X}$ as the countable union of sets ${E_1,E_2,\ldots \in {\mathcal B}_0}$ for which ${\mu_0(E_n) < \infty}$ for all ${n}$ . Show that ${\mu}$ and ${\mu'}$ agree on their common domain of definition. In other words, show that ${\mu(E) = \mu'(E)}$ for all ${E \in {\mathcal B} \cap {\mathcal B}'}$ . (Hint: first show that ${\mu'(E) \leq \mu^*(E)}$ for all ${E \in {\mathcal B}'}$ .)

Exercise 16 The purpose of this exercise is to show that the ${\sigma}$ -finite hypothesis in Exercise 15 cannot be removed. Let ${{\mathcal A}}$ be the collection of all subsets in ${{\bf R}}$ that can be expressed as finite unions of half-open intervals ${[a,b)}$ . Let ${\mu_0: {\mathcal A} \rightarrow [0,+\infty]}$ be the function such that ${\mu_0(E)=+\infty}$ for non-empty ${E}$ and ${\mu_0(\emptyset)=0}$ .

Show that ${\mu_0}$ is a pre-measure.

Show that ${\langle {\mathcal A} \rangle}$ is the Borel ${\sigma}$ -algebra ${{\mathcal B}[{\bf R}]}$ .

Show that the Hahn-Kolmogorov extension ${\mu: {\mathcal B}[{\bf R}] \rightarrow [0,+\infty]}$ of ${\mu_0}$ assigns an infinite measure to any non-empty Borel set.

Show that counting measure ${\#}$ (or more generally, ${c\#}$ for any ${c \in (0,+\infty]}$ ) is another extension of ${\mu_0}$ on ${{\mathcal B}[{\bf R}]}$ .

Exercise 17 Let ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ be a pre-measure which is ${\sigma}$ -finite (thus ${X}$ is the countable union of sets in ${{\mathcal B_0}}$ of finite ${\mu_0}$ -measure), and let ${\mu: {\mathcal B} \rightarrow [0,+\infty]}$ be the Hahn-Kolmogorov extension of ${\mu_0}$ .

Show that if ${E \in {\mathcal B}}$ , then there exists ${F \in \langle {\mathcal B}_0 \rangle}$ containing ${E}$ such that ${\mu(F \backslash E) = 0}$ (thus ${F}$ consists of the union of ${E}$ and a null set). Furthermore, show that ${F}$ can be chosen to be a countable intersection ${F = \bigcap_{n=1}^\infty F_n}$ of sets ${F_n}$ , each of which is a countable union ${F_n = \bigcup_{m=1}^\infty F_{n,m}}$ of sets ${F_{n,m}}$ in ${{\mathcal B}_0}$ .

If ${E \in {\mathcal B}}$ has finite measure (i.e. ${\mu(E) < \infty}$ ), and ${\varepsilon > 0}$ , show that there exists ${F \in {\mathcal B}_0}$ such that ${\mu(E \Delta F) \leq \varepsilon}$ .

Conversely, if ${E}$ is a set such that for every ${\varepsilon > 0}$ there exists ${F \in {\mathcal B}_0}$ such that ${\mu^*(E \Delta F) \leq \varepsilon}$ , show that ${E \in {\mathcal B}}$ .

— 3. Lebesgue-Stieltjes measure —

Now we use the Hahn-Kolmogorov extension theorem to construct a variety of measures. We begin with Lebesgue-Stieltjes measure.

Theorem 18 (Existence of Lebesgue-Stieltjes measure) Let ${F: {\bf R} \rightarrow {\bf R}}$ be a monotone non-decreasing function, and define the left and right limits

$\displaystyle F_-(x) := \sup_{y<x} F(y); \quad F_+(x) := \inf_{y>x} F(y),$

thus one has ${F_-(x) \leq F(x) \leq F_+(x)}$ for all ${x}$ . Let ${{\mathcal B}[{\bf R}]}$ be the Borel ${\sigma}$ -algebra on ${{\bf R}}$ . Then there exists a unique Borel measure ${\mu_F: {\mathcal B}[{\bf R}] \rightarrow [0,+\infty]}$ such that

$\displaystyle \mu_F( [a,b] ) = F_+(b)-F_-(a), \mu_F( [a,b) ) = F_-(b)-F_-(a), \ \ \ \ \ (3)$

$\displaystyle \mu_F( (a,b] ) = F_+(b)-F_+(a), \mu_F( (a,b) ) = F_-(b) - F_+(a)$

for all ${-\infty < b < a < \infty}$ , and

$\displaystyle \mu_F( \{a\} ) = F_+(a) - F_-(a) \ \ \ \ \ (4)$

for all ${a \in {\bf R}}$ .

Proof: (Sketch) For this proof, we will deviate from our previous notational conventions, and allow intervals to be unbounded, thus in particular including the half-infinite intervals ${[a,+\infty)}$ , ${(a,+\infty)}$ , ${(-\infty,a]}$ , ${(-\infty,a)}$ and the doubly infinite interval ${(-\infty,+\infty)}$ as intervals.
Define the ${F}$ -volume ${|I|_F \in [0,+\infty]}$ of any interval ${I}$ to be the required value of ${\mu_F(I)}$ given by (3) (e.g., ${|[a,b]|_F = F_+(b)-F_-(a)}$ ), adopting the obvious conventions that ${F_-(+\infty) = \sup_{y \in {\bf R}} F(y)}$ and ${F_+(-\infty) = \inf_{y \in {\bf R}} F(y)}$ , and also adopting the convention that the empty interval ${\emptyset}$ has zero ${F}$ -volume, ${|\emptyset|_F = 0}$ . Note that ${F_-(+\infty)}$ could equal ${+\infty}$ and ${F_+(-\infty)}$ could equal ${-\infty}$ , but in all circumstances the ${F}$ -volume ${|I|_F}$ is well-defined and takes values in ${[0,+\infty]}$ , after adopting the obvious conventions to evaluate expressions such as ${+\infty - (-\infty)}$ .
A somewhat tedious case check (Exercise!) gives the additivity property

$\displaystyle |I \cup J|_F = |I|_F + |J|_F$

whenever ${I}$ , ${J}$ are disjoint intervals that share a common endpoint. As a corollary, we see that if a interval ${I}$ is partitioned into finitely many disjoint sub-intervals ${I_1,\ldots,I_k}$ , we have ${|I| = |I_1|+\ldots+|I_k|}$ .
Let ${{\mathcal B}_0}$ be the Boolean algebra generated by the (possibly infinite) intervals, then ${{\mathcal B}_0}$ consists of those sets that can be expressed as a finite union of intervals. (This is slightly larger than the elementary algebra, as it allows for half-infinite intervals such as ${[0,+\infty)}$ , whereas the elementary algebra does not.) We can define a measure ${\mu_0}$ on this algebra by declaring

$\displaystyle \mu_0( E ) = |I_1|_F + \ldots + |I_k|_F$

whenever ${E=I_1 \cup \ldots \cup I_k}$ is the disjoint union of finitely many intervals. One can check (Exercise!) that this measure is well-defined (in the sense that it gives a unique value to ${\mu_0(E)}$ for each ${E \in {\mathcal B}_0}$ ) and is finitely additive. We now claim that ${\mu_0}$ is a pre-measure: thus we suppose that ${E = {\mathcal B}_0}$ is the disjoint union of countably many sets ${E_1, E_2, \ldots \in {\mathcal B}_0}$ , and wish to show that

$\displaystyle \mu_0(E) = \sum_{n=1}^\infty \mu_0(E_n).$

By splitting up ${E}$ into intervals and then intersecting each of the ${E_n}$ with these intervals and using finite additivity, we may assume that ${E}$ is a single interval. By splitting up the ${E_n}$ into their component intervals and using finite additivity, we may assume that the ${E_n}$ are also individual intervals. By finite additivity, we have ${ \mu_0(E) \geq \sum_{n=1}^N \mu_0(E_n)}$ for every ${N}$ , so it suffices to show that

$\displaystyle \mu_0(E) \leq \sum_{n=1}^\infty \mu_0(E_n).$

By the definition of ${\mu_0(E)}$ , one can check that

$\displaystyle \mu_0(E) = \sup_{K \subset E} \mu_0(K) \ \ \ \ \ (5)$

where ${K}$ ranges over all compact intervals contained in ${E}$ (Exercise!). Thus, it suffices to show that

$\displaystyle \mu_0(K) \leq \sum_{n=1}^\infty \mu_0(E_n)$

for each compact sub-interval ${K}$ of ${E}$ . In a similar spirit, one can show that

$\displaystyle \mu_0(E_n) = \inf_{U \supset E_n} \mu_0(U)$

where ${U}$ ranges over all open intervals containing ${E_n}$ (Exercise!). Using the ${\varepsilon/2^n}$ trick, it thus suffices to show that

$\displaystyle \mu_0(K) \leq \sum_{n=1}^\infty \mu_0(U_n)$

whenever ${U_n}$ is an open interval containing ${E_n}$ . But by the Heine-Borel theorem, one can cover ${K}$ by a finite number ${\bigcup_{n=1}^N U_n}$ of the ${U_n}$ , hence by finite subadditivity

$\displaystyle \mu_0(K) \leq\sum_{n=1}^N \mu_0(U_n)$

and the claim follows.
As ${\mu_0}$ is now verified to be a pre-measure, we may use the Hahn-Kolmogorov extension theorem to extend it to a countably additive measure ${\mu}$ on a ${\sigma}$ -algebra ${{\mathcal B}}$ that contains ${{\mathcal B}_0}$ . In particular, ${{\mathcal B}}$ contains all the elementary sets and hence (by Exercise 14 of Notes 3) contains the Borel ${\sigma}$ -algebra. Restricting ${\mu}$ to the Borel ${\sigma}$ -algebra we obtain the existence claim.
Finally, we establish uniqueness. If ${\mu'}$ is another Borel measure with the stated properties, then ${\mu'(K) = |K|_F}$ for every compact interval ${K}$ , and hence by (5) and upward monotone convergence, one has ${\mu'(I) = |I|_F}$ for every interval (including the unbounded ones). This implies that ${\mu'}$ agrees with ${\mu_0}$ on ${{\mathcal B}_0}$ , and thus (by Exercise 15, noting that ${\mu_0}$ is ${\sigma}$ -finite) agrees with ${\mu}$ on Borel measurable sets. $\Box$

Exercise 19 Verify the claims marked “Exercise!” in the above proof.

The measure ${\mu_F}$ given by the above theorem is known as the Lebesgue-Stieltjes measure ${\mu_F}$ of ${F}$ . (In some texts, this measure is only defined when ${F}$ is right-continuous, or equivalently if ${F=F_+}$ .)

Exercise 20 Define a Radon measure on ${{\bf R}}$ to be a Borel measure ${\mu}$ obeying the following additional properties:

(Local finiteness) ${\mu(K) < \infty}$ for every compact ${K}$ .

(Inner regularity) One has ${\mu(E) = \sup_{K \subset E, K \hbox{ compact}} \mu(K)}$ for every Borel set ${E}$ .

(Outer regularity) One has ${\mu(E) = \inf_{U \supset E, U \hbox{ open}} \mu(U)}$ for every Borel set ${E}$ .

Show that for every monotone function ${F: {\bf R} \rightarrow {\bf R}}$ , the Lebesgue-Stieltjes measure ${\mu_F}$ is a Radon measure on ${{\bf R}}$ ; conversely, if ${\mu}$ is a Radon measure on ${{\bf R}}$ , show that there exists a monotone function ${F: {\bf R} \rightarrow {\bf R}}$ such that ${\mu= \mu_F}$ .

Radon measures will be studied in more detail in 245B.

Exercise 21 (Near uniqueness) If ${F, F':{\bf R} \rightarrow {\bf R}}$ are monotone non-decreasing functions, show that ${\mu_F = \mu_{F'}}$ if and only if there exists a constant ${C \in {\bf R}}$ such that ${F_+(x) = F'_+(x) + C}$ and ${F_-(x) = F'_-(x) + C}$ for all ${x \in {\bf R}}$ . Note that this implies that the value of ${F}$ at its points of discontinuity are irrelevant for the purposes of determining the Lebesgue-Stieltjes measure ${\mu_F}$ ; in particular, ${\mu_F = \mu_{F_+} = \mu_{F_-}}$ .

In the special case when ${F_+(-\infty)=0}$ and ${F_-(+\infty)=1}$ , then ${\mu_F}$ is a probability measure, and ${F_+(x) = \mu_F((-\infty,x])}$ is known as the cumulative distribution function of ${\mu_F}$ .
Now we give some examples of Lebesgue-Stieltjes measure.

Exercise 22 (Lebesgue-Stieltjes measure, absolutely continuous case)

If ${F: {\bf R} \rightarrow {\bf R}}$ is the identity function ${F(x)=x}$ , show that ${\mu_F}$ is equal to Lebesgue measure ${m}$ .

If ${F: {\bf R} \rightarrow {\bf R}}$ is monotone non-decreasing and absolutely continuous (which in particular implies that ${F'}$ exists and is absolutely integrable, show that ${\mu_F = m_{F'}}$ in the sense of Exercise 47 of Notes 3, thus
$\displaystyle \mu_F(E) = \int_E F'(x)\ dx$

for any Borel measurable ${E}$ , and

$\displaystyle \int_{\bf R} f(x)\ d\mu_F(x) = \int_{\bf R} f(x) F'(x)\ dx$

for any unsigned Borel measurable ${f: {\bf R} \rightarrow [0,+\infty]}$ .

In view of the above exercise, the integral ${\int_{\bf R} f\ d\mu_F}$ is often abbreviated ${\int_{\bf R} f\ dF}$ , and referred to as the Lebesgue-Stieltjes integral of ${f}$ with respect to ${F}$ . In particular, observe the identity

$\displaystyle \int_{[a,b]}\ dF = F_+(b) - F_-(a)$

for any monotone non-decreasing ${F: {\bf R} \rightarrow {\bf R}}$ and any ${-\infty < a < b < +\infty}$ , which can be viewed as yet another formulation of the fundamental theorem of calculus.

Exercise 23 (Lebesgue-Stieltjes measure, pure point case)

If ${H: {\bf R} \rightarrow {\bf R}}$ is the Heaviside function ${H := 1_{[0,+\infty)}}$ , show that ${\mu_H}$ is equal to the Dirac measure ${\delta_0}$ at the origin (defined in Example 9 of Notes 3).

If ${F = \sum_n c_n J_n}$ is a jump function (as defined in Definition 17 of Notes 5), show that ${\mu_F}$ is equal to the linear combination ${\sum c_n \delta_{x_n}}$ of delta functions (as defined in Exercise 22 of Notes 3), where ${x_n}$ is the point of discontinuity for the basic jump function ${J_n}$ .

Exercise 24 (Lebesgue-Stieltjes measure, singular continuous case)

If ${F: {\bf R} \rightarrow {\bf R}}$ is a monotone non-decreasing function, show that ${F}$ is continuous if and only if ${\mu_F(\{x\})=0}$ for all ${x \in {\bf R}}$ .

If ${F}$ is the Cantor function (defined in Exercise 46 of Notes 5), show that ${\mu_F}$ is a probability measure supported on the middle-thirds Cantor set (Exercise 10 from Notes 1) in the sense that ${\mu_F({\bf R} \backslash C) = 0}$ . The measure ${\mu_F}$ is known as Cantor measure.

If ${\mu_F}$ is Cantor measure, establish the self-similarity properties ${\mu( \frac{1}{3} \cdot E ) = \frac{1}{2} \mu(E)}$ and ${\mu( \frac{1}{3} \cdot E + \frac{2}{3} ) = \frac{1}{2} \mu(E)}$ for every Borel-measurable ${E \subset [0,1]}$ , where ${\frac{1}{3} \cdot E := \{ \frac{1}{3} x: x \in E \}}$ .

Exercise 25 (Connection with Riemann-Stieltjes integral) Let ${F: {\bf R} \rightarrow {\bf R}}$ be monotone non-decreasing, let ${[a,b]}$ be a compact interval, and let ${f: [a,b] \rightarrow {\bf R}}$ be continuous. Suppose that ${F}$ is continuous at the endpoints ${a, b}$ of the interval. Show that for every ${\varepsilon > 0}$ there exists ${\delta > 0}$ such that

$\displaystyle |\sum_{i=1}^n f(t^*_i) (F(t_i) - F(t_{i-1})) - \int_{[a,b]} f\ dF| \leq \varepsilon$

whenever ${a = t_0 < t_1 < \ldots < t_n = b}$ and ${t^*_i \in [t_{i-1},t_i]}$ for ${1 \leq i \leq n}$ are such that ${\sup_{1 \leq i \leq n} |t_i - t_{i-1}| \leq \delta}$ . In the language of the Riemann-Stieltjes integral, this result asserts that the Lebesgue-Stieltjes integral extends the Riemann-Stieltjes integral.

Exercise 26 (Integration by parts formula) Let ${F, G: {\bf R} \rightarrow {\bf R}}$ be monotone non-decreasing and continuous. Show that

$\displaystyle \int_{[a,b]} F\ dG = - \int_{[a,b]} G\ dF + F(b) G(b) - F(a) G(a)$

for any compact interval ${[a,b]}$ . (Hint: use Exercise \ref}{riemstil}.) This formula can be partially extended to the case when one or both of ${F, G}$ have discontinuities, but care must be taken when ${F}$ and ${G}$ are simultaneously discontinuous at the same location.

— 4. Product measure —

Given two sets ${X}$ and ${Y}$ , one can form their Cartesian product ${X \times Y = \{ (x,y): x \in X, y \in Y \}}$ . This set is naturally equipped with the coordinate projection maps ${\pi_X: X \times Y \rightarrow X}$ and ${\pi_Y: X \times Y \rightarrow Y}$ defined by setting ${\pi_X(x,y) := x}$ and ${\pi_Y(x,y) := y}$ . One can certainly take Cartesian products ${X_1 \times \ldots \times X_d}$ of more than two sets, or even take an infinite product ${\prod_{\alpha \in A} X_\alpha}$ , but for simplicity we will only discuss the theory for products of two sets for now.
Now suppose that ${(X,{\mathcal B}_X)}$ and ${(Y,{\mathcal B}_Y)}$ are measurable spaces. Then we can still form the Cartesian product ${X \times Y}$ and the projection maps ${\pi_X: X \times Y \rightarrow X}$ and ${\pi_Y: X \times Y \rightarrow Y}$ . But now we can also form the pullback ${\sigma}$ -algebras

$\displaystyle \pi_X^*({\mathcal B}_X) := \{ \pi_X^{-1}(E): E \in {\mathcal B}_X \} = \{ E \times Y: E \in {\mathcal B}_X \}$

and

$\displaystyle \pi_Y^*({\mathcal B}_Y) := \{ \pi_Y^{-1}(E): E \in {\mathcal B}_Y \} = \{ X \times F: F \in {\mathcal B}_Y \}.$

We then define the product ${\sigma}$ -algebra ${{\mathcal B}_X \times {\mathcal B}_Y}$ to be the ${\sigma}$ -algebra generated by the union of these two ${\sigma}$ -algebras:

$\displaystyle {\mathcal B}_X \times {\mathcal B}_Y := \langle \pi_X^*({\mathcal B}_X) \cup \pi_Y^*({\mathcal B}_Y) \rangle.$

This definition has several equivalent formulations:

Exercise 27 Let ${(X,{\mathcal B}_X)}$ and ${(Y,{\mathcal B}_Y)}$ be measurable spaces.

Show that ${{\mathcal B}_X \times {\mathcal B}_Y}$ is the ${\sigma}$ -algebra generated by the sets ${E \times F}$ with ${E \in {\mathcal B}_X}$ , ${Y \in {\mathcal B}_Y}$ . In other words, ${{\mathcal B}_X \times {\mathcal B}_Y}$ is the coarsest ${\sigma}$ -algebra on ${X \times Y}$ with the property that the product of a ${{\mathcal B}_X}$ -measurable set and a ${{\mathcal B}_Y}$ -measurable set is always ${{\mathcal B}_X \times {\mathcal B}_Y}$ measurable.

Show that ${{\mathcal B}_X \times {\mathcal B}_Y}$ is the coarsest ${\sigma}$ -algebra on ${X \times Y}$ that makes the projection maps ${\pi_X, \pi_Y}$ both measurable morphisms (see Remark 8 from Notes 3).

If ${E \in {\mathcal B}_X \times {\mathcal B}_Y}$ , show that the sets ${E_x := \{ y \in Y: (x,y) \in E \}}$ lie in ${{\mathcal B}_Y}$ for every ${x \in X}$ , and similarly that the sets ${E^y := \{ x \in X: (x,y) \in E \}}$ lie in ${{\mathcal B}_X}$ for every ${y \in Y}$ .

If ${f: X \times Y \rightarrow [0,+\infty]}$ is measurable (with respect to ${{\mathcal B}_X \times {\mathcal B}_Y}$ ), show that the function ${f_x: y \mapsto f(x,y)}$ is ${{\mathcal B}_Y}$ -measurable for every ${x \in X}$ , and similarly that the function ${f^y: x \mapsto f(x,y)}$ is ${{\mathcal B}_X}$ -measurable for every ${y \in Y}$ .

If ${E \in {\mathcal B}_X \times {\mathcal B}_Y}$ , show that the slices ${E_x := \{ y \in Y: (x,y) \in E \}}$ lie in a countably generated ${\sigma}$ -algebra. In other words, show that there exists an at most countable collection ${{\mathcal A} = {\mathcal A}_E}$ of sets (which can depend on ${E}$ ) such that ${\{ E_x: x \in X \} \subset \langle {\mathcal A} \rangle}$ . Conclude in particular that the number of distinct slices ${E_x}$ is at most ${c}$ , the cardinality of the continuum. (The last part of this exercise is only suitable for students who are comfortable with cardinal arithmetic.)

Exercise 28

Show that the product of two trivial ${\sigma}$ -algebras (on two different spaces ${X,Y}$ ) is again trivial.

(Exercise removed)

Show that the product of two finite ${\sigma}$ -algebras is again finite.

Show that the product of two Borel ${\sigma}$ -algebras (on two Euclidean spaces ${{\bf R}^d, {\bf R}^{d'}}$ with ${d,d' \geq 1}$ ) is again the Borel ${\sigma}$ -algebra (on ${{\bf R}^d \times {\bf R}^{d'} \equiv {\bf R}^{d+d'}}$ ).

Show that the product of two Lebesgue ${\sigma}$ -algebras (on two Euclidean spaces ${{\bf R}^d, {\bf R}^{d'}}$ with ${d,d' \geq 1}$ ) is not the Lebesgue ${\sigma}$ -algebra. (Hint: argue by contradiction and use Exercise 27(3).)

However, show that the Lebesgue ${\sigma}$ -algebra on ${{\bf R}^{d+d'}}$ is the completion of the product of the Lebesgue ${\sigma}$ -algebras of ${{\bf R}^d}$ and ${{\bf R}^{d'}}$ with respect to ${d+d'}$ -dimensional Lebesgue measure (see Exercise 26 of Notes 3 for the definition of completion of a measure space).

This part of the exercise is only for students who are comfortable with cardinal arithmetic. Give an example to show that the product of two discrete ${\sigma}$ -algebras is not necessarily discrete.

On the other hand, show that the product of two discrete ${\sigma}$ -algebras ${2^X, 2^Y}$ is again a discrete ${\sigma}$ -algebra if at least one of the domains ${X, Y}$ is at most countably infinite.

Now suppose we have two measure spaces ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ . Given that we can multiply together the sets ${X}$ and ${Y}$ to form a product set ${X \times Y}$ , and can multiply the ${\sigma}$ -algebras ${{\mathcal B}_X}$ and ${{\mathcal B}_Y}$ together to form a product ${\sigma}$ -algebra ${{\mathcal B}_X \times {\mathcal B}_Y}$ , it is natural to expect that we can multiply the two measures ${\mu_X: {\mathcal B}_X \rightarrow [0,+\infty]}$ and ${\mu_Y: {\mathcal B}_Y \rightarrow [0,+\infty]}$ to form a product measure ${\mu_X \times \mu_Y: {\mathcal B}_X \times {\mathcal B}_Y \rightarrow [0,+\infty]}$ . In view of the “base times height formula” that one learns in elementary school, one expects to have

$\displaystyle \mu_X \times \mu_Y( E \times F ) = \mu_X(E) \mu_Y(F) \ \ \ \ \ (6)$

whenever ${E \in {\mathcal B}_X}$ and ${F \in {\mathcal B}_Y}$ .
To construct this measure, it is convenient to make the assumption that both spaces are ${\sigma}$ -finite.

Definition 29 ( ${\sigma}$ -finite) A measure space ${(X,{\mathcal B},\mu)}$ is ${\sigma}$ -finite if ${X}$ can be expressed as the countable union of sets of finite measure.

Thus, for instance, ${{\bf R}^d}$ with Lebesgue measure is ${\sigma}$ -finite, as ${{\bf R}^d}$ can be expressed as the union of (for instance) the balls ${B(0,n)}$ for ${n=1,2,3,\ldots}$ , each of which has finite measure. On the other hand, ${{\bf R}^d}$ with counting measure is not ${\sigma}$ -finite (why?). But most measure spaces that one actually encounters in analysis (including, clearly, all probability spaces) are ${\sigma}$ -finite. It is possible to partially extend the theory of product spaces to the non- ${\sigma}$ -finite setting, but there are a number of very delicate technical issues that arise and so we will not discuss them here.
As long as we restrict attention to the ${\sigma}$ -finite case, product measure always exists and is unique:

Proposition 30 (Existence and uniqueness of product measure) Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be ${\sigma}$ -finite measure spaces. Then there exists a unique measure ${\mu_X \times \mu_Y}$ on ${{\mathcal B}_X \times {\mathcal B}_Y}$ that obeys ${\mu_X \times \mu_Y( E \times F ) = \mu_X(E) \mu_Y(F)}$ whenever ${E \in {\mathcal B}_X}$ and ${F \in {\mathcal B}_Y}$ .

Proof: We first show existence. Inspired by the fact that Lebesgue measure is the Hahn-Kolmogorov completion of elementary (pre-)measure, we shall first construct an “elementary product pre-measure” that we will then apply Theorem 14 to.
Let ${{\mathcal B}_0}$ be the collection of all finite unions

$\displaystyle S := (E_1 \times F_1) \cup \ldots \cup (E_k \times F_k)$

of Cartesian products of ${{\mathcal B}_X}$ -measurable sets ${E_1,\ldots,E_k}$ and ${{\mathcal B}_Y}$ -measurable sets ${F_1,\ldots,F_k}$ . (One can think of such sets as being somewhat analogous to elementary sets in Euclidean space, although the analogy is not perfectly exact.) It is not difficult to verify that this is a Boolean algebra (though it is not, in general, a ${\sigma}$ -algebra). Also, any set in ${{\mathcal B}_0}$ can be easily decomposed into a disjoint union of product sets ${E_1 \times F_1, \ldots, E_k \times F_k}$ of ${{\mathcal B}_X}$ -measurable sets and ${{\mathcal B}_Y}$ -measurable sets (cf. Lemma 2 (and Exercise 2) from the prologue). We then define the quantity ${\mu_0(S)}$ associated such a disjoint union ${S}$ by the formula

$\displaystyle \mu_0(S) := \sum_{j=1}^k \mu_X(E_j) \mu_Y(F_j)$

whenever ${S}$ is the disjoint union of products ${E_1 \times F_1,\ldots,E_k \times F_k}$ of ${{\mathcal B}_X}$ -measurable sets and ${{\mathcal B}_Y}$ -measurable sets. One can show that this definition does not depend on exactly how ${S}$ is decomposed, and gives a finitely additive measure ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ (cf. Exercise 2 from the prologue, and also Exercise 31 from Notes 3).
Now we show that ${\mu_0}$ is a pre-measure. It suffices to show that if ${S \in {\mathcal B}_0}$ is the countable disjoint union of sets ${S_1, S_2, \ldots \in {\mathcal B}_0}$ , then ${\mu_0(S) = \sum_{n=1}^\infty \mu_0(S_n)}$ .
Splitting ${S}$ up into disjoint product sets, and restricting the ${S_n}$ to each of these product sets in turn, we may assume without loss of generality (using the finite additivity of ${\mu_0}$ ) that ${S = E \times F}$ for some ${E \in {\mathcal B}_X}$ and ${F \in {\mathcal B}_Y}$ . In a similar spirit, by breaking each ${S_n}$ up into component product sets and using finite additivity again, we may assume without loss of generality that each ${S_n}$ takes the form ${S_n = E_n \times F_n}$ for some ${E_n \in {\mathcal B}_X}$ and ${F_n \in {\mathcal B}_Y}$ . By definition of ${\mu_0}$ , our objective is now to show that

$\displaystyle \mu_X(E) \mu_Y(F) = \sum_{n=1}^\infty \mu_X(E_n) \mu_Y(F_n).$

To do this, first observe from construction that we have the pointwise identity

$\displaystyle 1_E(x) 1_F(y) = \sum_{n=1}^\infty 1_{E_n}(x) 1_{F_n}(y)$

for all ${x \in X}$ and ${y \in Y}$ . We fix ${x \in X}$ , and integrate this identity in ${y}$ (noting that both sides are measurable and unsigned) to conclude that

$\displaystyle \int_Y 1_E(x) 1_F(y)\ d\mu_Y(y) = \int_Y \sum_{n=1}^\infty 1_{E_n}(x) 1_{F_n}(y)\ d\mu_Y(y).$

The left-hand side simplifies to ${1_E(x) \mu_Y(F)}$ . To compute the right-hand side, we use the monotone convergence theorem to interchange the summation and integration, and soon see that the right-hand side is ${\sum_{n=1}^\infty 1_{E_n}(x) \mu_Y(F_n)}$ , thus

$\displaystyle 1_E(x) \mu_Y(F) = \sum_{n=1}^\infty 1_{E_n}(x) \mu_Y(F_n)$

for all ${x}$ . Both sides are measurable and unsigned in ${x}$ , so we may integrate in ${X}$ and conclude that

$\displaystyle \int_X 1_E(x) \mu_Y(F)\ d\mu_X = \int_X \sum_{n=1}^\infty 1_{E_n}(x) \mu_Y(F_n)\ d\mu_X(x).$

The left-hand side here is ${\mu_X(E) \mu_Y(F)}$ . Using monotone convergence as before, the right-hand side simplifies to ${\sum_{n=1}^\infty \mu_X(E_n) \mu_Y(F_n)}$ , and the claim follows.
Now that we have established that ${\mu_0}$ is a pre-measure, we may apply Theorem 14 to extend this measure to a countably additive measure ${\mu_X \times \mu_Y}$ on a ${\sigma}$ -algebra containing ${{\mathcal B}_0}$ . By Exercise 27(2), ${\mu_X \times \mu_Y}$ is a countably additive measure on ${{\mathcal B}_X \times {\mathcal B}_Y}$ , and as it extends ${\mu_0}$ , it will obey (6). Finally, to show uniqueness, observe from finite additivity that any measure ${\mu_X \times \mu_Y}$ on ${{\mathcal B}_X \times {\mathcal B}_Y}$ that obeys (6) must extend ${\mu_0}$ , and so uniqueness follows from Exercise 15. $\Box$

Remark 31 When ${X}$ , ${Y}$ are not both ${\sigma}$ -finite, then one can still construct at least one product measure, but it will, in general, not be unique. This makes the theory much more subtle, and we will not discuss it in these notes.

Example 32 From Exercise 22 of Notes 1, we see that the product ${m^d \times m^{d'}}$ of the Lebesgue measures ${m^d, m^{d'}}$ on ${({\bf R}^d,{\mathcal L}[{\bf R}^d])}$ and ${({\bf R}^d,{\mathcal L}[{\bf R}^{d'}])}$ respectively will agree with Lebesgue measure ${m^{d+d'}}$ on the product space ${{\mathcal L}[{\bf R}^d] \times {\mathcal L}[{\bf R}^{d'}]}$ , which as noted in Exercise 28 is a subalgebra of ${{\mathcal L}[{\bf R}^{d+d'}]}$ . After taking the completion ${\overline{m^d \times m^{d'}}}$ of this product measure, one obtains the full Lebesgue measure ${m^{d+d'}}$ .

Exercise 33 Let ${(X,{\mathcal B}_X)}$ , ${(Y,{\mathcal B}_Y)}$ be measurable spaces.

Show that the product of two Dirac measures on ${(X,{\mathcal B}_X)}$ , ${(Y,{\mathcal B}_Y)}$ is a Dirac measure on ${(X \times Y, {\mathcal B}_X \times {\mathcal B}_Y)}$ .

If ${X, Y}$ are at most countable, show that the product of the two counting measures on ${(X,{\mathcal B}_X)}$ , ${(Y,{\mathcal B}_Y)}$ is the counting measure on ${(X \times Y, {\mathcal B}_X \times {\mathcal B}_Y)}$ .

Exercise 34 (Associativity of product) Let ${(X,{\mathcal B}_X,\mu_X)}$ , ${(Y,{\mathcal B}_Y,\mu_Y)}$ , ${(Z,{\mathcal B}_Z,\mu_Z)}$ be ${\sigma}$ -finite sets. We may identify the Cartesian products ${(X \times Y) \times Z}$ and ${X \times (Y \times Z)}$ with each other in the obvious manner. If we do so, show that ${({\mathcal B}_X \times {\mathcal B}_Y) \times {\mathcal B}_Z = {\mathcal B}_X \times ({\mathcal B}_Y \times {\mathcal B}_Z)}$ and ${(\mu_X \times \mu_Y) \times \mu_Z = \mu_X \times (\mu_Y \times \mu_Z)}$ .

Now we integrate using this product measure. We will need the following technical lemma. Define a monotone class in ${X}$ is a collection ${{\mathcal B}}$ of subsets of ${X}$ with the following two closure properties:

If ${E_1 \subset E_2 \subset \ldots}$ are a countable increasing sequence of sets in ${{\mathcal B}}$ , then ${\bigcup_{n=1}^\infty E_n \in {\mathcal B}}$ .
If ${E_1 \supset E_2 \supset \ldots}$ are a countable decreasing sequence of sets in ${{\mathcal B}}$ , then ${\bigcap_{n=1}^\infty E_n \in {\mathcal B}}$ .

Lemma 35 (Monotone class lemma) Let ${{\mathcal A}}$ be a Boolean algebra on ${X}$ . Then ${\langle {\mathcal A} \rangle}$ is the smallest monotone class that contains ${{\mathcal A}}$ .

Proof: Let ${{\mathcal B}}$ be the intersection of all the monotone classes that contain ${{\mathcal A}}$ . Since ${\langle {\mathcal A} \rangle}$ is clearly one such class, ${{\mathcal B}}$ is a subset of ${\langle {\mathcal A} \rangle}$ . Our task is then to show that ${{\mathcal B}}$ contains ${\langle {\mathcal A} \rangle}$ .
It is also clear that ${{\mathcal B}}$ is a monotone class that contains ${{\mathcal A}}$ . By replacing all the elements of ${{\mathcal B}}$ with their complements, we see that ${{\mathcal B}}$ is necessarily closed under complements.
For any ${E \in {\mathcal A}}$ , consider the set ${{\mathcal C}_E}$ of all sets ${F \in {\mathcal B}}$ such that ${F \backslash E}$ , ${E \backslash F}$ , ${F \cap E}$ , and ${X \backslash (E \cup F)}$ all lie in ${{\mathcal B}}$ . It is clear that ${{\mathcal C}_E}$ contains ${{\mathcal A}}$ ; since ${{\mathcal B}}$ is a monotone class, we see that ${{\mathcal C}_E}$ is also. By definition of ${{\mathcal B}}$ , we conclude that ${{\mathcal C}_E = {\mathcal B}}$ for all ${E \in {\mathcal A}}$ .
Next, let ${{\mathcal D}}$ be the set of all ${E \in {\mathcal B}}$ such that ${F \backslash E}$ , ${E \backslash F}$ , ${F \cap E}$ , and ${X \backslash (E \cup F)}$ all lie in ${{\mathcal B}}$ for all ${F \in {\mathcal B}}$ . By the previous discussion, we see that ${{\mathcal D}}$ contains ${{\mathcal A}}$ . One also easily verifies that ${{\mathcal D}}$ is a monotone class. By definition of ${{\mathcal B}}$ , we conclude that ${{\mathcal D} = {\mathcal B}}$ . Since ${{\mathcal B}}$ is also closed under complements, this implies that ${{\mathcal B}}$ is closed with respect to finite unions. Since this class also contains ${{\mathcal A}}$ , which contains ${\emptyset}$ , we conclude that ${{\mathcal B}}$ is a Boolean algebra. Since ${{\mathcal B}}$ is also closed under increasing countable unions, we conclude that it is closed under arbitrary countable unions, and is thus a ${\sigma}$ -algebra. As it contains ${{\mathcal A}}$ , it must also contain ${\langle {\mathcal A} \rangle}$ . $\Box$

Theorem 36 (Tonelli’s theorem, incomplete version) Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be ${\sigma}$ -finite measure spaces, and let ${f: X \times Y \rightarrow [0,+\infty]}$ be measurable with respect to ${{\mathcal B}_X \times {\mathcal B}_Y}$ . Then:

The functions ${x \mapsto \int_Y f(x,y)\ d\mu_Y(y)}$ and ${y \mapsto \int_X f(x,y)\ d\mu_X(x)}$ (which are well-defined, thanks to Exercise 27) are measurable with respect to ${{\mathcal B}_X}$ and ${{\mathcal B}_Y}$ respectively.

We have
$\displaystyle \int_{X \times Y} f(x,y)\ d\mu_X \times \mu_Y(x,y)$

$\displaystyle = \int_X (\int_Y f(x,y)\ d\mu_Y(y))\ d\mu_X(x)$

$\displaystyle = \int_Y (\int_X f(x,y)\ d\mu_X(x))\ d\mu_Y(y).$

Proof: By writing the ${\sigma}$ -finite space ${X}$ as an increasing union ${X = \bigcup_{n=1}^\infty X_n}$ of finite measure sets, we see from several applications of the monotone convergence theorem that it suffices to prove the claims with ${X}$ replaced by ${X_n}$ . Thus we may assume without loss of generality that ${X}$ has finite measure. Similarly we may assume ${Y}$ has finite measure. Note from (6) that this implies that ${X \times Y}$ has finite measure also.
Every unsigned measurable function is the increasing limit of unsigned simple functions. By several applications of the monotone convergence theorem, we thus see that it suffices to verify the claim when ${f}$ is a simple function. By linearity, it then suffices to verify the claim when ${f}$ is an indicator function, thus ${f=1_S}$ for some ${S \in {\mathcal B}_X \times {\mathcal B}_Y}$ .
Let ${{\mathcal C}}$ be the set of all ${S \in {\mathcal B}_X \times {\mathcal B}_Y}$ for which the claims hold. From the repeated applications of the monotone convergence theorem and the downward monotone convergence theorem (which is available in this finite measure setting) we see that ${{\mathcal C}}$ is a monotone class.
By direct computation (using (6)), we see that ${{\mathcal C}}$ contains as an element any product ${S = E \times F}$ with ${E \in {\mathcal B}_X}$ and ${F \in {\mathcal B}_Y}$ . By finite additivity, we conclude that ${{\mathcal C}}$ also contains as an element any a disjoint finite union ${S = E_1 \times F_1 \cup \ldots \cup E_k \times F_k}$ of such products. This implies that ${{\mathcal C}}$ also contains the Boolean algebra ${{\mathcal B}_0}$ in the proof of Proposition 30, as such sets can always be expressed as the disjoint finite union of Cartesian products of measurable sets. Applying the monotone class lemma, we conclude that ${{\mathcal C}}$ contains ${\langle {\mathcal B}_0 \rangle = {\mathcal B}_X \times {\mathcal B}_Y}$ , and the claim follows. $\Box$

Remark 37 Note that Tonelli’s theorem for sums (Theorem 2 from Notes 1) is a special case of the above result when ${\mu_X, \mu_Y}$ are counting measure. In a similar spirit, Corollary 15 from Notes 3 is the special case when just one of ${\mu_X, \mu_Y}$ is counting measure.

Corollary 38 Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be ${\sigma}$ -finite measure spaces, and let ${E \in {\mathcal B}_X \times {\mathcal B}_Y}$ be a null set with respect to ${\mu_X \times \mu_Y}$ . Then for ${\mu_X}$ -almost every ${x \in X}$ , the set ${E_x := \{ y \in Y: (x,y) \in E \}}$ is a ${\mu_Y}$ -null set; and similarly, for ${\mu_Y}$ -almost every ${y \in Y}$ , the set ${E^y := \{ x \in X: (x,y) \in E \}}$ is a ${\mu_X}$ -null set.

Proof: Applying the Tonelli theorem to the indicator function ${1_E}$ , we conclude that

$\displaystyle 0 = \int_X (\int_Y 1_E(x,y)\ d\mu_Y(y))\ d\mu_X(x) = \int_Y (\int_X 1_E(x,y)\ d\mu_X(x))\ d\mu_Y(y)$

and thus

$\displaystyle 0 = \int_X \mu_Y(E_x)\ d\mu_X(x) = \int_Y \mu_X(E^y)\ d\mu_Y(y),$

and the claim follows. $\Box$
With this corollary, we can extend Tonelli’s theorem to the completion ${(X \times Y, \overline{{\mathcal B}_X \times {\mathcal B}_Y}, \overline{\mu_X \times \mu_Y})}$ of the product space ${(X \times Y, {\mathcal B}_X \times {\mathcal B}_Y, \mu_X \times \mu_Y)}$ : (see Exercise 26 of Notes 3 for the definition of completion). But we can easily extend the Tonelli theorem to this context:

Theorem 39 (Tonelli’s theorem, complete version) Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be complete ${\sigma}$ -finite measure spaces, and let ${f: X \times Y \rightarrow [0,+\infty]}$ be measurable with respect to ${\overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ . Then:

For ${\mu_X}$ -almost every ${x \in X}$ , the function ${y \mapsto f(x,y)}$ is ${{\mathcal B}_Y}$ -measurable, and in particular ${\int_Y f(x,y)\ d\mu_Y(y)}$ exists. Furthermore, the ( ${\mu_X}$ -almost everywhere defined) map ${x \mapsto \int_Y f(x,y)\ d\mu_Y}$ is ${{\mathcal B}_X}$ -measurable.

For ${\mu_Y}$ -almost every ${y \in Y}$ , the function ${x \mapsto f(x,y)}$ is ${{\mathcal B}_X}$ -measurable, and in particular ${\int_X f(x,y)\ d\mu_X(x)}$ exists. Furthermore, the ( ${\mu_Y}$ -almost everywhere defined) map ${y \mapsto \int_X f(x,y)\ d\mu_X}$ is ${{\mathcal B}_Y}$ -measurable.

We have
$\displaystyle \int_{X \times Y} f(x,y)\ d\overline{\mu_X \times \mu_Y}(x,y)$

$\displaystyle = \int_X (\int_Y f(x,y)\ d\mu_Y(y))\ d\mu_X(x) \ \ \ \ \ (7)$

$\displaystyle = \int_Y (\int_X f(x,y)\ d\mu_X(x))\ d\mu_Y(y).$

Proof: From Exercise 26 of Notes 3, every measurable set in ${\overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ is equal to a measurable set in ${{\mathcal B}_X \times {\mathcal B}_Y}$ outside of a ${\mu_X \times \mu_Y}$ -null set. This implies that the ${\overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ -measurable function ${f}$ agrees with a ${{\mathcal B}_X \times {\mathcal B}_Y}$ -measurable function ${\tilde f}$ outside of a ${\mu_X \times \mu_Y}$ -null set ${E}$ (as can be seen by expressing ${f}$ as the limit of simple functions). From Corollary 38, we see that for ${\mu_X}$ -almost every ${x \in X}$ , the function ${y \mapsto f(x,y)}$ agrees with ${y \mapsto \tilde f(x,y)}$ outside of a ${\mu_Y}$ -null set (and is in particular measurable, as ${(Y,{\mathcal B}_Y,\mu_Y)}$ is complete); and similarly for ${\mu_Y}$ -almost every ${y \in Y}$ , the function ${x \mapsto f(x,y)}$ agrees with ${x \mapsto \tilde f(x,y)}$ outside of a ${\mu_X}$ -null set and is measurable, and the claim follows. $\Box$
Specialising to the case when ${f}$ is an indicator function ${f=1_E}$ , we conclude

Corollary 40 (Tonelli’s theorem for sets) Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be complete ${\sigma}$ -finite measure spaces, and let ${E \in \overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ . Then:

For ${\mu_X}$ -almost every ${x \in X}$ , the set ${E_x := \{ y \in Y: (x,y) \in E \}}$ lies in ${{\mathcal B}_Y}$ , and the ( ${\mu_X}$ -almost everywhere defined) map ${x \mapsto \mu_Y(E_x)}$ is ${{\mathcal B}_X}$ -measurable.

For ${\mu_Y}$ -almost every ${y \in Y}$ , the set ${E^y := \{ x \in X: (x,y) \in E \}}$ lies in ${{\mathcal B}_X}$ , and the ( ${\mu_Y}$ -almost everywhere defined) map ${y \mapsto \mu_X(E^y)}$ is ${{\mathcal B}_Y}$ -measurable.

We have
$\displaystyle \overline{\mu_X \times \mu_Y}(E) = \int_X \mu_Y(E_x)\ d\mu_X(x) \ \ \ \ \ (8)$

$\displaystyle = \int_Y \mu_X(E^y)\ d\mu_Y(y).$

Exercise 41 The purpose of this exercise is to demonstrate that Tonelli’s theorem can fail if the ${\sigma}$ -finite hypothesis is removed, and also that product measure need not be unique. Let ${X}$ is the unit interval ${[0,1]}$ with Lebesgue measure ${m}$ (and the Lebesgue ${\sigma}$ -algebra ${{\mathcal L}([0,1])}$ ) and ${Y}$ is the unit interval ${[0,1]}$ with counting measure (and the discrete ${\sigma}$ -algebra ${2^{[0,1]}}$ ) ${\#}$ . Let ${f := 1_E}$ be the indicator function of the diagonal ${E := \{(x,x): x \in [0,1]\}}$ .

Show that ${f}$ is measurable in the product ${\sigma}$ -algebra.

Show that ${\int_X (\int_Y f(x,y)\ d\#(y)) dm(x) = 1}$ .

Show that ${\int_Y (\int_X f(x,y)\ dm(x)) d\#(y) = 0}$ .

Show that there is more than one measure ${\mu}$ on ${{\mathcal L}([0,1]) \times 2^{[0,1]}}$ with the property that ${\mu(E \times F) = m(E) \#(F)}$ for all ${E \in {\mathcal L}([0,1])}$ and ${F \in 2^{[0,1]}}$ . (Hint: use the two different ways to perform a double integral to create two different measures.)

Remark 42 If ${f}$ is not assumed to be measurable in the product space (or its completion), then of course the expression ${\int_{X \times Y} f(x,y)\ d\overline{\mu_X \times \mu_Y}(x,y)}$ does not make sense. Furthermore, in this case the remaining two expressions in (7) may become different as well (in some models of set theory, at least), even when ${X}$ and ${Y}$ are finite measure. For instance, let us assume the continuum hypothesis, which implies that the unit interval ${[0,1]}$ can be placed in one-to-one correspondence with the first uncountable ordinal ${\omega_1}$ . Let ${\prec}$ be the ordering of ${[0,1]}$ that is associated to this ordinal, let ${E := \{ (x,y) \in [0,1]^2: x \prec y \}}$ , and let ${f := 1_E}$ . Then, for any ${y \in [0,1]}$ , there are at most countably many ${x}$ such that ${x \prec y}$ , and so ${\int_{[0,1]} f(x,y)\ dx}$ exists and is equal to zero for every ${y}$ . On the other hand, for every ${x \in [0,1]}$ , one has ${x \prec y}$ for all but countably many ${y \in [0,1]}$ , and so ${\int_{[0,1]} f(x,y)\ dy}$ exists and is equal to one for every ${y}$ , and so the last two expressions in (7) exist but are unequal. (In particular, Tonelli’s theorem implies that ${E}$ cannot be a Lebesgue measurable subset of ${[0,1]^2}$ .) Thus we see that measurability in the product space is an important hypothesis. (There do however exist models of set theory (with the axiom of choice) in which such counterexamples cannot be constructed, at least in the case when ${X}$ and ${Y}$ are the unit interval with Lebesgue measure.)

Tonelli’s theorem is for the unsigned integral, but it leads to an important analogue for the absolutely integral, known as Fubini’s theorem:

Theorem 43 (Fubini’s theorem) Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be complete ${\sigma}$ -finite measure spaces, and let ${f: X \times Y \rightarrow {\bf C}}$ be absolutely integrable with respect to ${\overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ . Then:

For ${\mu_X}$ -almost every ${x \in X}$ , the function ${y \mapsto f(x,y)}$ is absolutely integrable with respect to ${\mu_Y}$ , and in particular ${\int_Y f(x,y)\ d\mu_Y(y)}$ exists. Furthermore, the ( ${\mu_X}$ -almost everywhere defined) map ${x \mapsto \int_Y f(x,y)\ d\mu_Y(y)}$ is absolutely integrable with respect to ${\mu_X}$ .

For ${\mu_Y}$ -almost every ${y \in Y}$ , the function ${x \mapsto f(x,y)}$ is absolutely integrable with respect to ${\mu_X}$ , and in particular ${\int_X f(x,y)\ d\mu_X(x)}$ exists. Furthermore, the ( ${\mu_Y}$ -almost everywhere defined) map ${y \mapsto \int_X f(x,y)\ d\mu_X(x)}$ is absolutely integrable with respect to ${\mu_Y}$ .

We have
$\displaystyle \int_{X \times Y} f(x,y)\ d\overline{\mu_X \times \mu_Y}(x,y)$

$\displaystyle = \int_X (\int_Y f(x,y)\ d\mu_Y(y))\ d\mu_X(x)$

$\displaystyle = \int_Y (\int_X f(x,y)\ d\mu_X(x))\ d\mu_Y(y).$

Proof: By taking real and imaginary parts we may assume that ${f}$ is real; by taking positive and negative parts we may assume that ${f}$ is unsigned. But then the claim follows from Tonelli’s theorem; note from (7) that ${\int_X (\int_Y f(x,y)\ d\mu_Y(y))\ d\mu_X(x)}$ is finite, and so ${\int_Y f(x,y)\ d\mu_Y(y) < \infty}$ for ${\mu_X}$ -almost every ${x \in X}$ , and similarly ${\int_X f(x,y)\ d\mu_X(x) < \infty}$ for ${\mu_Y}$ -almost every ${y \in Y}$ . $\Box$

Exercise 44 Give an example of a Borel measurable function ${f: [0,1]^2 \rightarrow {\bf R}}$ such that the integrals ${\int_{[0,1]} f(x,y)\ dy}$ and ${\int_{[0,1]} f(x,y)\ dx}$ exist and are absolutely integrable for all ${x \in [0,1]}$ and ${y \in [0,1]}$ respectively, and that ${\int_{[0,1]} (\int_{[0,1]} f(x,y)\ dy)\ dx}$ and ${\int_{[0,1]} (\int_{[0,1]} f(x,y)\ dx)\ dy}$ exist and are absolutely integrable, but such that

$\displaystyle \int_{[0,1]} (\int_{[0,1]} f(x,y)\ dy)\ dx \neq \int_{[0,1]} (\int_{[0,1]} f(x,y)\ dx)\ dy$

are unequal. (Hint: adapt the example from Remark 2 of Notes 1.) Thus we see that Fubini’s theorem fails when one drops the hypothesis that ${f}$ is absolutely integrable with respect to the product space.

Remark 45 Despite the failure of Tonelli’s theorem in the non- ${\sigma}$ -finite setting, it is possible to (carefully) extend Fubini’s theorem to the non- ${\sigma}$ -finite setting, as the absolute integrability hypotheses, when combined with Markov’s inequality, can provide a substitute for the ${\sigma}$ -finite property. However, we will not do so here, and indeed I would recommend proceeding with extreme caution when performing any sort of interchange of integrals or invoking of product measure when one is not in the ${\sigma}$ -finite setting.

Informally, Fubini’s theorem allows one to always interchange the order of two integrals, as long as the integrand is absolutely integrable in the product space (or its completion). In particular, specialising to Lebesgue measure, we have

$\displaystyle \int_{{\bf R}^{d+d'}} f(x,y)\ d(x,y) = \int_{{\bf R}^d} (\int_{{\bf R}^{d'}} f(x,y)\ dy)\ dx = \int_{{\bf R}^{d'}} (\int_{{\bf R}^d} f(x,y)\ dx)\ dy$

whenever ${f: {\bf R}^{d+d'} \rightarrow {\bf C}}$ is absolutely integrable. In view of this, we often write ${dx dy}$ (or ${dy dx}$ ) for ${d(x,y)}$ .
By combining Fubini’s theorem with Tonelli’s theorem, we can recast the absolute integrability hypothesis:

Corollary 46 (Fubini-Tonelli theorem) Let ${(X,{\mathcal B}_X,\mu_X)}$ and ${(Y,{\mathcal B}_Y,\mu_Y)}$ be complete ${\sigma}$ -finite measure spaces, and let ${f: X \times Y \rightarrow {\bf C}}$ be measurable with respect to ${\overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ . If

$\displaystyle \int_X (\int_Y |f(x,y)|\ d\mu_Y(y))\ d\mu_X(x) < \infty$

(note the left-hand side always exists, by Tonelli’s theorem) then ${f}$ is absolutely integrable with respect to ${\overline{{\mathcal B}_X \times {\mathcal B}_Y}}$ , and in particular the conclusions of Fubini’s theorem hold. Similarly if we use ${\int_Y (\int_X |f(x,y)|\ d\mu_X(x))\ d\mu_Y(y)}$ instead of ${\int_X (\int_Y |f(x,y)|\ d\mu_Y)\ d\mu_X}$ .

The Fubini-Tonelli theorem is an indispensable tool for computing integrals. We give some basic examples below:

Exercise 47 (Area interpretation of integral) Let ${(X,{\mathcal B},\mu)}$ be a ${\sigma}$ -finite measure space, and let ${{\bf R}}$ be equipped with Lebesgue measure ${m}$ and the Borel ${\sigma}$ -algebra ${{\mathcal B}[{\bf R}]}$ . Show that if ${f: X \rightarrow [0,+\infty]}$ is measurable, then the set ${ \{ (x,t) \in X \times {\bf R}: 0 \leq t \leq f(x) \}}$ is measurable in ${{\mathcal B} \times {\mathcal B}[{\bf R}]}$ , and

$\displaystyle (\mu \times m)( \{ (x,t) \in X \times {\bf R}: 0 \leq t \leq f(x) \} ) = \int_X f(x)\ d\mu(x).$

Similarly if we replace ${\{ (x,t) \in X \times {\bf R}: 0 \leq t \leq f(x) \}}$ by ${ \{ (x,t) \in X \times {\bf R}: 0 \leq t < f(x) \}}$ .

Exercise 48 (Distribution formula) Let ${(X,{\mathcal B},\mu)}$ be a ${\sigma}$ -finite measure space, and let ${f: X \rightarrow [0,+\infty]}$ be measurable. Show that

$\displaystyle \int_X f(x)\ d\mu(x) = \int_{[0,+\infty]} \mu( \{ x \in X: f(x) \geq \lambda \} )\ d\lambda.$

(Note that the integrand on the right-hand side is monotone and thus Lebesgue measurable.) Similarly if we replace ${\{ x \in X: f(x) \geq \lambda \}}$ by ${\{ x \in X: f(x) > \lambda \}}$ .

Exercise 49 (Approximations to the identity) Let ${P: {\bf R}^d \rightarrow {\bf R}^+}$ be a good kernel (see Exercise 26 from Notes 5), and let ${P_t}$ be the associated rescaled functions. Show that if ${f: {\bf R}^d \rightarrow {\bf C}}$ is absolutely integrable, that ${f*P_t}$ converges in ${L^1}$ norm to ${f}$ as ${t \rightarrow 0}$ . (Hint: use the density argument. You will need an upper bound on ${\|f*P_t\|_{L^1({\bf R}^d)}}$ which can be obtained using Tonelli’s theorem.)

— 5. Application: the Radamacher differentiation theorem (Optional) —

The Fubini-Tonelli theorem is often used in extending lower-dimensional results to higher-dimensional ones. We illustrate this by extending the one-dimensional Lipschitz differentiation theorem (Exercise 40 from Notes 5) to higher dimensions. We first recall some higher-dimensional definitions:

Definition 50 (Lipschitz continuity) A function ${f: X \rightarrow Y}$ from one metric space ${(X,d_X)}$ to another ${(Y,d_Y)}$ is said to be Lipschitz continuous if there exists a constant ${C>0}$ such that ${d_Y(f(x),f(x')) \leq C d_X(x,x')}$ for all ${x,x' \in X}$ . (In our current application, ${X}$ will be ${{\bf R}^d}$ and ${Y}$ will be ${{\bf R}}$ , with the usual metrics.)

Exercise 51 Show that Lipschitz continuous functions are uniformly continuous, and hence continuous. Then give an example of a uniformly continuous function ${f: [0,1] \rightarrow [0,1]}$ that is not Lipschitz continuous.

Definition 52 (Differentiability) Let ${f: {\bf R}^d \rightarrow {\bf R}}$ be a function, and let ${x_0 \in {\bf R}^d}$ . For any ${v \in {\bf R}^d}$ , we say that ${f}$ is directionally differentiable at ${x_0}$ in the direction ${v}$ if the limit

$\displaystyle D_v f(x_0) := \lim_{h \rightarrow 0; h \in {\bf R} \backslash \{0\}} \frac{f(x_0+hv) - f(x_0)}{h}$

exists, in which case we call ${D_v f(x_0)}$ the directional derivative of ${f}$ at ${x_0}$ in this direction. If ${v=e_i}$ is one of the standard basis vectors ${e_1,\ldots,e_d}$ of ${{\bf R}^d}$ , we write ${D_v f(x_0)}$ as ${\frac{\partial f}{\partial x_i}(x_0)}$ , and refer to this as the partial derivative of ${f}$ at ${x_0}$ in the ${e_i}$ direction.
We say that ${f}$ is totally differentiable at ${x_0}$ if there exists a vector ${\nabla f(x_0) \in {\bf R}^d}$ with the property that

$\displaystyle \lim_{h \rightarrow 0; h \rightarrow {\bf R}^d \backslash \{0\}} \frac{f(x_0+h) - f(x_0) - h \cdot \nabla f(x_0)}{|h|} = 0,$

where ${v \cdot w}$ is the usual dot product on ${{\bf R}^d}$ . We refer to ${\nabla f(x_0)}$ (if it exists) as the gradient of ${f}$ at ${x_0}$ .

Remark 53 From the viewpoint of differential geometry, it is better to work not with the gradient vector ${\nabla f(x_0) \in {\bf R}^d}$ , but rather with the derivative covector ${df(x_0): {\bf R}^d \rightarrow {\bf R}}$ given by ${df(x_0): v \mapsto \nabla f(x_0) \cdot v}$ . This is because one can then define the notion of total differentiability without any mention of the Euclidean dot product, which allows one to extend this notion to other manifolds in which there is no Euclidean (or more generally, Riemannian) structure. However, as we are working exclusively in Euclidean space for this application, this distinction will not be important for us.

Total differentiability implies directional and partial differentiability, but not conversely, as the following three exercises demonstrate.

Exercise 54 (Total differentiability implies directional and partial differentiability) Show that if ${f: {\bf R}^d \rightarrow {\bf R}}$ is totally differentiable at ${x_0}$ , then it is directionally differentiable at ${x_0}$ in each direction ${v \in {\bf R}^d}$ , and one has the formula

$\displaystyle D_v f(x_0) = v \cdot \nabla f(x_0). \ \ \ \ \ (9)$

In particular, the partial derivatives ${\frac{\partial f}{\partial x_i} f(x_0)}$ exist for ${i=1,\ldots,d}$ and

$\displaystyle \nabla f(x_0) = (\frac{\partial f}{\partial x_1}(x_0), \ldots, \frac{\partial f}{\partial x_d}(x_0)). \ \ \ \ \ (10)$

Exercise 55 (Continuous partial differentiability implies total differentiability) Let ${f: {\bf R}^d \rightarrow {\bf R}}$ be such that the partial derivatives ${\frac{\partial f}{\partial x_i}: {\bf R}^d \rightarrow {\bf R}}$ exist everywhere and are continuous. Then show that ${f}$ is totally differentiable everywhere, which in particular implies that the gradient is given by the formula (10) and the directional derivatives are given by (9).

Exercise 56 (Directional differentiability does not imply total differentiability) Let ${f: {\bf R}^2 \rightarrow {\bf R}}$ be defined by setting ${f(0,0) := 0}$ and ${f(x_1,x_2) := \frac{x_1 x_2^2}{x_1^2+x_2^2}}$ for ${(x_1,x_2) \in {\bf R}^2 \backslash \{(0,0)\}}$ . Show that the directional derivatives ${D_v f(x)}$ exist for all ${x,v \in {\bf R}^2}$ (so in particular, the partial derivatives exist), but that ${f}$ is not totally differentiable at the origin ${(0,0)}$ .

Now we can state the Rademacher differentiation theorem.

Theorem 57 (Rademacher differentiation theorem) Let ${f: {\bf R}^d \rightarrow {\bf R}}$ be Lipschitz continuous. Then ${f}$ is totally differentiable at ${x_0}$ for almost every ${x_0 \in {\bf R}^d}$ .

Note that the ${d=1}$ case of this theorem is Exercise 40 from Notes 5, and indeed we will use the one-dimensional theorem to imply the higher-dimensional one, though there will be some technical issues due to the gap between directional and total differentiability.
Proof: The strategy here is to first aim for the more modest goal of directional differentiability, and then find a way to link the directional derivatives together to get total differentiability.
Let ${v, x_0 \in {\bf R}^d}$ . As ${f}$ is continuous, we see that in order for the directional derivative

$\displaystyle D_v f(x_0) := \lim_{h \rightarrow 0; h \in {\bf R} \backslash \{0\}} \frac{f(x_0+hv) - f(x_0)}{h}$

to exist, it suffices to let ${h}$ range in the dense subset ${{\bf Q} \backslash \{0\}}$ of ${{\bf R} \backslash \{0\}}$ for the purposes of determing whether the limit exists. In particular, ${D_v f(x_0)}$ exists if and only if

$\displaystyle \limsup_{h \rightarrow 0; h \in {\bf Q} \backslash \{0\}} \frac{f(x_0+hv) - f(x_0)}{h} = \liminf_{h \rightarrow 0; h \in {\bf Q} \backslash \{0\}} \frac{f(x_0+hv) - f(x_0)}{h}.$

From this we easily conclude that for each direction ${v \in {\bf R}^d}$ , the set

$\displaystyle E_v := \{ x_0 \in {\bf R}^d: D_v f(x_0) \hbox{ does not exist} \}$

is Lebesgue measurable in ${{\bf R}^d}$ (indeed, it is even Borel measurable). A similar argument reveals that ${D_v f}$ is a measurable function outside of ${E_v}$ . From the Lipschitz nature of ${f}$ , we see that ${D_v f}$ is also a bounded function.
Now we claim that ${E_v}$ is a null set for each ${v}$ . For ${v=0}$ ${E_v}$ is clearly empty, so we may assume ${v \neq 0}$ . Applying an invertible linear transformation to map ${v}$ to ${e_1}$ (noting that such transformations will map Lipschitz functions to Lispchitz functions, and null sets to null sets) we may assume without loss of generality that ${v}$ is the basis vector ${e_1}$ . Thus our task is now to show that ${\frac{\partial f}{\partial x_1}(x)}$ exists for almost every ${x \in {\bf R}^d}$ .
We now split ${{\bf R}^d}$ as ${{\bf R} \times {\bf R}^{d-1}}$ . For each ${x_0 \in {\bf R}}$ and ${y_0 \in {\bf R}^{d-1}}$ , we see from the definitions that ${\frac{\partial f}{\partial x_1}(x_0,y_0)}$ exists if and only if the one-dimensional function ${x \mapsto f(x,y_0)}$ is differentiable at ${x_0}$ . But this function is Lipschitz continuous (this is inherited from the Lipschitz continuity of ${f}$ ), and so we see that for each fixed ${y_0 \in {\bf R}^{d-1}}$ , the set ${E^{y_0} := \{ x_0 \in {\bf R}: (x_0,y_0) \in E \}}$ is a null set in ${{\bf R}}$ . Applying Tonelli’s theorem for sets (Corollary 40), we conclude that ${E}$ is a null set as required.
We would like to now conclude that ${\bigcup_{v \in {\bf R}^d} E_v}$ is a null set, but there are uncountably many ${v}$ ‘s, so this is not directly possible. However, as ${{\bf Q}^d}$ is rational, we can at least assert that ${E := \bigcup_{v \in {\bf Q}^d} E_v}$ is a null set. In particular, for almost every ${x_0 \in {\bf R}^d}$ , ${f}$ is directionally differentiable in every rational direction ${v \in {\bf Q}^d}$ .
Now we perform an important trick, in which we interpret the directional derivative ${D_v f}$ as a weak derivative. We already know that ${D_v f}$ is almost everywhere defined, bounded and measurable. Now let ${g: {\bf R}^d \rightarrow {\bf R}}$ be any function that is compactly supported and Lipschitz continuous. We investigate the integral

$\displaystyle \int_{{\bf R}^d} D_v f(x) g(x)\ dx.$

This integral is absolutely convergent since ${D_v f(x)}$ is bounded and measurable, and ${g(x)}$ is continuous and compactly supported, hence bounded. We expand this out as

$\displaystyle \int_{{\bf R}^d} \lim_{h \rightarrow 0; h \in {\bf R} \backslash \{0\}} \frac{f(x+hv)-f(x)}{h} g(x)\ dx.$

Note (from the Lipschitz nature of ${f}$ ) that the expression ${\frac{f(x+hv)-f(x)}{h} g(x)}$ is bounded uniformly in ${h}$ and ${x}$ , and is also uniformly compactly supported in ${x}$ for ${h}$ in a bounded set. We may thus apply the Lebesgue dominated convergence theorem to pull the limit out of the integral to obtain

$\displaystyle \lim_{h \rightarrow 0; h \in {\bf R} \backslash \{0\}} \int_{{\bf R}^d} \frac{f(x+hv)-f(x)}{h} g(x)\ dx.$

Now, from translation invariance of the Lebesgue integral (Exercise 15) we have

$\displaystyle \int_{{\bf R}^d} f(x+hv) g(x)\ dx = \int_{{\bf R}^d} f(x) g(x-hv)\ dx$

and so (by the lienarity of the Lebesgue integral) we may rearrange the previous expression as

$\displaystyle \lim_{h \rightarrow 0; h \in {\bf R} \backslash \{0\}} \int_{{\bf R}^d} f(x) \frac{g(x-hv)-g(x)}{h}\ dx.$

Now, as ${g}$ is Lipschitz, we know that ${\frac{g(x-hv)-g(x)}{h}}$ is uniformly bounded and converges pointwise almost everywhere to ${D_{-v} g(x)}$ as ${h \rightarrow 0}$ . We may thus apply the dominated convergence theorem again and end up with the integration by parts formula

$\displaystyle \int_{{\bf R}^d} D_v f(x) g(x)\ dx = \int_{{\bf R}^d} f(x) D_{-v} g(x)\ dx. \ \ \ \ \ (11)$

This formula moves the directional derivative operator ${D_v}$ from ${f}$ over to ${g}$ . At present, this does not look like much of an advantage, because ${g}$ is the same sort of function that ${f}$ is. However, the key point is that we can choose ${g}$ to be whatever we please, whereas ${f}$ is fixed. In particular, we can choose ${g}$ to be a compactly supported, continuously differentiable function (such functions are Lipschitz from the fundamental theorem of calculus, as their derivatives are bounded). By Exercise 55, one has ${D_{-v} g = - v \cdot \nabla g}$ for such functions, and so

$\displaystyle \int_{{\bf R}^d} D_v f(x) g(x)\ dx = - \int_{{\bf R}^d} f(x) (v \cdot \nabla g)(x)\ dx.$

The right-hand side is linear in ${v}$ , and so the left-hand side must be linear in ${v}$ also. In particular, if ${v = (v_1,\ldots,v_d)}$ , then we have

$\displaystyle \int_{{\bf R}^d} D_v f(x) g(x)\ dx = \sum_{j=1}^d v_j \int_{{\bf R}^d} D_{e_j} f(x) g(x)\ dx.$

If we define the gradient candidate function

$\displaystyle \nabla f(x) := (D_{e_1} f(x), \ldots, D_{e_d} f(x)) = (\frac{\partial f}{\partial x_1}(x), \ldots, \frac{\partial f}{\partial x_d}(x))$

(note that this function is well-defined almost everywhere, even though we don’t know yet whether ${f}$ is totally differentiable almost everywhere), we thus have

$\displaystyle \int_{{\bf R}^d} (D_v f - v \cdot \nabla f)(x) g(x)\ dx = 0$

for all compactly supported, continuously differentiable ${g}$ . This implies (see Exercise 58 below) that ${F_v := D_v f - v \cdot \nabla f}$ vanishes almost everywhere, thus (by countable subadditivity) we have

$\displaystyle D_v f(x_0) = v \cdot \nabla f(x_0) \ \ \ \ \ (12)$

for almost every ${x_0 \in {\bf R}^d}$ and every ${v \in {\bf Q}^d}$ .
Let ${x_0}$ be such that (12) holds for all ${v \in {\bf Q}^d}$ . We claim that this forces ${f}$ to be totally differentiable at ${x_0}$ , which would give the claim. Let ${F: {\bf R}^d \rightarrow {\bf R}^d}$ be the modified function

$\displaystyle F(h) := f(x_0+h) - f(x_0) - h \cdot \nabla f(x_0).$

Our objective is to show that

$\displaystyle \lim_{h \rightarrow 0; h \in {\bf R}^d \backslash \{0\}} |F(h)| / |h| = 0.$

On the other hand, we have ${F(0)=0}$ , ${F}$ is Lipschitz, and from (12) we see that ${D_v F(0) = 0}$ for every ${v \in {\bf Q}^d}$ .
Let ${\varepsilon > 0}$ , and suppose that ${h \in {\bf R}^d \backslash \{0\}}$ . Then we can write ${h = r u}$ where ${r := |h|}$ and ${u := h/|h|}$ lies on the unit sphere. This ${u}$ need not lie in ${{\bf Q}^d}$ , but we can approximate it by some vector ${v \in {\bf Q}^d}$ with ${|u-v| \leq \varepsilon}$ . Furthermore, by the total boundedness of the unit sphere, we can make ${v}$ lie in a finite subset ${V_\varepsilon}$ of ${{\bf Q}^d}$ that only depends on ${\varepsilon}$ (and on ${d}$ ).
Since ${D_v F(0) = 0}$ for all ${v \in V_\varepsilon}$ , we see (by making ${|h|}$ small enough depending on ${V_\varepsilon}$ ) that we have

$\displaystyle |\frac{F(rv)-F(0)}{r}| \leq \varepsilon$

for all ${v \in V_\varepsilon}$ , and thus

$\displaystyle |F(rv)| \leq \varepsilon r.$

On the other hand, from the Lipschitz nature of ${F}$ , we have

$\displaystyle |F(ru) - F(rv)| \leq C r |u-v| \leq C r \varepsilon$

where ${C}$ is the Lipschitz constant of ${F}$ . As ${h=ru}$ , we conclude that

$\displaystyle |F(h)| \leq (C+1) r \varepsilon.$

In other words, we have shown that

$\displaystyle |F(h)|/|h| \leq (C+1)\varepsilon$

whenever ${|h|}$ is sufficiently small depending on ${\varepsilon}$ . Letting ${\varepsilon \rightarrow 0}$ , we obtain the claim. $\Box$

Exercise 58 Let ${F: {\bf R}^d \rightarrow {\bf R}}$ be a locally integrable function with the property that ${\int_{{\bf R}^d} F(x) g(x)\ dx=0}$ whenever ${g}$ is a compactly supported, continuously differentiable function. Show that ${F}$ is zero almost everywhere. (Hint: if not, use the Lebesgue differentiation theorem to find a Lebesgue point ${x_0}$ of ${F}$ for which ${F(x_0) \neq 0}$ , then pick a ${g}$ which is supported in a sufficiently small neighbourhood of ${x_0}$ .)

— 6. Infinite product spaces and the Kolmogorov extension theorem (optional) —

In Section 4 we considered the product of two sets, measurable spaces, or ( ${\sigma}$ -finite) measure spaces. We now consider how to generalise this concept to products of more than two such spaces. The axioms of set theory allow us to form a Cartesian product ${X_A := \prod_{\alpha \in A} X_\alpha}$ of any family ${(X_\alpha)_{\alpha \in A}}$ of sets indexed by another set ${A}$ , which consists of the space of all tuples ${x_A = (x_\alpha)_{\alpha \in A}}$ indexed by ${A}$ , for which ${x_\alpha \in X_\alpha}$ for all ${\alpha \in A}$ . This concept allows for a succinct formulation of the axiom of choice (Axiom 3 from Notes 1), namely that an arbitrary Cartesian product of non-empty sets remains non-empty.
For any ${\beta \in A}$ , we have the coordinate projection maps ${\pi_\beta: X_A \rightarrow X_\beta}$ defined by ${\pi_\beta( (x_\alpha)_{\alpha \in A} ) := x_\beta}$ . More generally, given any ${B \subset A}$ , we define the partial projections ${\pi_B: X_A \rightarrow X_B}$ to the partial product space ${X_B := \prod_{\alpha \in B} X_\alpha}$ by ${\pi_B( (x_\alpha)_{\alpha \in A} ) := (x_\alpha)_{\alpha \in B}}$ . More generally still, given two subsets ${C \subset B \subset A}$ , we have the partial subprojections ${\pi_{C \leftarrow B}: X_B \rightarrow X_C}$ defined by ${\pi_{C \leftarrow B}( (x_\alpha)_{\alpha\in B} ) := (x_\alpha)_{\alpha \in C}}$ . These partial subprojections obey the composition law ${\pi_{D \leftarrow C} \circ \pi_{C \leftarrow B} := \pi_{D \leftarrow B}}$ for all ${D \subset C \subset B \subset A}$ (and thus form a very simple example of a category).
As before, given any ${\sigma}$ -algebra ${{\mathcal B}_\beta}$ on ${X_\beta}$ , we can pull it back by ${\pi_\beta}$ to create a ${\sigma}$ -algebra

$\displaystyle \pi_\beta^{*}({\mathcal B}_\beta) := \{ \pi_\beta^{-1}(E_\beta): E_\beta \in {\mathcal B}_\beta \}$

on ${X_A}$ . One easily verifies that this is indeed a ${\sigma}$ -algebra. Informally, ${\pi_\beta^{*}({\mathcal B}_\beta)}$ describes those sets (or “events”, if one is thinking in probabilistic terms) that depend only on the ${x_\beta}$ coordinate of the state ${x_A = (x_\alpha)_{\alpha \in A}}$ , and whose dependence on ${x_\beta}$ is ${{\mathcal B}_\beta}$ -measurable. We can then define the product ${\sigma}$ -algebra

$\displaystyle \prod_{\beta \in A} {\mathcal B}_\beta := \langle \bigcup_{\beta \in A} \pi_\beta^{*}({\mathcal B}_\beta) \rangle.$

We have a generalisation of Exercise 27:

Exercise 59 Let ${((X_\alpha,{\mathcal B}_\alpha))_{\alpha \in A}}$ be a family of measurable spaces. For any ${B \subset A}$ , write ${{\mathcal B}_B := \prod_{\beta \in B} {\mathcal B}_\beta}$ .

Show that ${{\mathcal B}_A}$ is the coarsest ${\sigma}$ -algebra on ${X_A}$ that makes the projection maps ${\pi_\beta}$ measurable morphisms for all ${\beta \in A}$ .

Show that for each ${B \subset A}$ , that ${\pi_B}$ is a measurable morphism from ${(X_A,{\mathcal B}_A)}$ to ${(X_B, {\mathcal B}_B)}$ .

If ${E}$ in ${{\mathcal B}_A}$ , show that there exists an at most countable set ${B \subset A}$ and a set ${E_B \in {\mathcal B}_B}$ such that ${E_A = \pi_B^{-1}(E_B)}$ . Informally, this asserts that a measurable event can only depend on at most countably many of the coefficients.

If ${f: X_A \rightarrow [0,+\infty]}$ is ${{\mathcal B}_A}$ -measurable, show that there exists an at most countable set ${B \subset A}$ and a ${{\mathcal B}_B}$ -measurable function ${f_B: X_B \rightarrow [0,+\infty]}$ such that ${f = f_B \circ \pi_B}$ .

If ${A}$ is at most countable, show that ${{\mathcal B}_A}$ is the ${\sigma}$ -algebra generated by the sets ${\prod_{\beta\in A} E_\beta}$ with ${E_\beta \in {\mathcal B}_\beta}$ for all ${\beta \in A}$ .

On the other hand, show that if ${A}$ is uncountable and the ${{\mathcal B}_\alpha}$ are all non-trivial, show that ${{\mathcal B}_A}$ is not the ${\sigma}$ -algebra generated by sets ${\prod_{\beta\in A} E_\beta}$ with ${E_\beta \in {\mathcal B}_\beta}$ for all ${\beta \in A}$ .

If ${B \subset A}$ , ${E \in {\mathcal B}_A}$ , and ${x_{A\backslash B} \in X_{A \backslash B}}$ , show that the set ${E_{x_{A\backslash B},B} := \{ x_B \in X_B: (x_B, x_{A \backslash B}) \in E \}}$ lies in ${{\mathcal B}_B}$ , where we identify ${X_B \times X_{A \backslash B}}$ with ${X_A}$ in the obvious manner.

If ${B \subset A}$ , ${f: X_A \rightarrow [0,+\infty]}$ is ${{\mathcal B}_A}$ -measurable, and ${x_{A\backslash B} \in X_{A \backslash B}}$ , show that the function ${f_{x_{A\backslash B},B}: x_B \rightarrow f(x_B, x_{A \backslash B})}$ is ${{\mathcal B}_B}$ -measurable.

Now we consider the problem of constructing a measure ${\mu_A}$ on the product space ${X_A}$ . Any such measure ${\mu_A}$ will induce pushforward measures ${\mu_B := (\pi_B)_* \mu_A}$ on ${X_B}$ (introduced in Exercise 36 of Notes 3), thus

$\displaystyle \mu_B(E_B) := \mu_A( \pi_B^{-1}(E_B) )$

for all ${E_B\in {\mathcal B}_B}$ . These measures obey the compatibility relation

$\displaystyle (\pi_{C \leftarrow B})_* \mu_B = \mu_C \ \ \ \ \ (13)$

whenever ${C \subset B \subset A}$ , as can be easily seen by chasing the definitions.
One can then ask whether one can reconstruct ${\mu_A}$ from just from the projections ${\mu_B}$ to finite subsets ${B}$ . This is possible in the important special case when the ${\mu_B}$ (and hence ${\mu_A}$ ) are probability measures, provided one imposes an additional inner regularity hypothesis on the measures ${\mu_B}$ . More precisely:

Definition 60 (Inner regularity) A (metrisable) inner regular measure space ${(X, {\mathcal B},\mu,d)}$ is a measure space ${(X,{\mathcal B},\mu)}$ equipped with a metric ${d}$ such that

Every compact set is measurable; and

One has ${\mu(E) = \sup_{K \subset E, K \hbox{ compact}} \mu(K)}$ for all measurable ${E}$ .

We say that ${\mu}$ is inner regular if it is associated to an inner regular measure space.

Thus for instance Lebesgue measure is inner regular, as are Dirac measures and counting measures. Indeed, most measures that one actually encounters in applications will be inner regular. For instance, any finite Borel measure on ${{\bf R}^d}$ (or more generally, on a locally compact, ${\sigma}$ -compact space) is inner regular (see Exercise 12 of 245B Notes 12). Inner regularity is one of the axioms of a Radon measure, which we will discuss in more detail in 245B.

Remark 61 One can generalise the concept of an inner regular measure space to one which is given by a topology rather than a metric; Kolmogorov’s extension theorem still holds in this more general setting, but requires Tychonoff’s theorem, which we will cover in 245B Notes 10. However, some minimal regularity hypotheses of a topological nature are needed to make the Kolmogorov extension theorem work, although this is usually not a severe restriction in practice.

Theorem 62 (Kolmogorov extension theorem) Let ${((X_\alpha,{\mathcal B}_\alpha),{\mathcal F}_\alpha)_{\alpha \in A}}$ be a family of measurable spaces ${(X_\alpha,{\mathcal B}_\alpha)}$ , equipped with a topology ${{\mathcal F}_\alpha}$ . For each finite ${B \subset A}$ , let ${\mu_B}$ be an inner regular probability measure on ${{\mathcal B}_B := \prod_{\alpha \in B} {\mathcal B}_\alpha}$ with the product topology ${{\mathcal F}_B := \prod_{\alpha \in B} {\mathcal F}_\alpha}$ , obeying the compatibility condition (13) whenever ${C \subset B \subset A}$ are two nested finite subsets of ${A}$ . Then there exists a unique probability measure ${\mu_A}$ on ${{\mathcal B}_A}$ with the property that ${(\pi_B)_* \mu_A = \mu_B}$ for all finite ${B \subset A}$ .

Proof: Our main tool here will be the Hahn-Kolmogorov extension theorem for pre-measures (Theorem 14), combined with the Heine-Borel theorem.
Let ${{\mathcal B}_0}$ be the set of all subsets of ${X_A}$ that are of the form ${\pi_B^{-1}( E_B )}$ for some finite ${B \subset A}$ and some ${E_B \in {\mathcal B}_B}$ . One easily verifies that this is a Boolean algebra that is contained in ${{\mathcal B}_A}$ . We define a function ${\mu_0: {\mathcal B}_0 \rightarrow [0,+\infty]}$ by setting

$\displaystyle \mu_0( E ) := \mu_B( E_B )$

whenever ${E}$ takes the form ${\pi_B^{-1}(E_B)}$ for some finite ${B \subset A}$ and ${E_B \in {\mathcal B}_B}$ . Note that a set ${E \in {\mathcal B}_0}$ may have two different representations ${E = \pi_B^{-1}(E_B) = \pi_{B'}^{-1}(E_{B'})}$ for some finite ${B,B' \subset A}$ , but then one must have ${E_B = \pi_{B \leftarrow B \cup B'}(E_{B \cup B'})}$ and ${E_{B'} = \pi_{B' \leftarrow B \cup B'}(E_{B \cup B'})}$ , where ${E_{B \cup B'} := \pi_{B \cup B'}(E)}$ . Applying (13), we see that

$\displaystyle \mu_B(E_B) = \mu_{B \cup B'}(E_{B \cup B'})$

and

$\displaystyle \mu_{B'}(E_{B'}) = \mu_{B \cup B'}(E_{B \cup B'})$

and thus ${\mu_B(E_B) = \mu_{B'}(E_{B'})}$ . This shows that ${\mu_0(E)}$ is well defined. As the ${\mu_B}$ are probability measures, we see that ${\mu_0(X_A)=1}$ .
It is not difficult to see that ${\mu_0}$ is finitely additive. We now claim that ${\mu_0}$ is a pre-measure. In other words, we claim that if ${E \in {\mathcal B}_0}$ is the disjoint countable union ${E = \bigcup_{n=1}^\infty E_n}$ of sets ${E_n \in {\mathcal B}_0}$ , then ${\mu_0(E) = \sum_{n=1}^\infty \mu_0(E_n)}$ .
For each ${N \geq 1}$ , let ${F_N := E \backslash \bigcup_{n=1}^N E_N}$ . Then the ${F_N}$ lie in ${{\mathcal B}_0}$ , are decreasing, and are such that ${\bigcap_{N=1}^\infty F_N = \emptyset}$ . By finite additivity (and the finiteness of ${\mu_0}$ ), we see that it suffices to show that ${\lim_{N \rightarrow \infty} \mu_0(F_N) = 0}$ .
Suppose this is not the case, then there exists ${\varepsilon > 0}$ such that ${\mu_0(F_N) > \varepsilon}$ for all ${N}$ . As each ${F_N}$ lies in ${{\mathcal B}_0}$ , we have ${F_N = \pi_{B_N}^{-1}(G_N)}$ for some finite sets ${B_N \subset A}$ and some ${{\mathcal B}_{B_N}}$ -measurable sets ${G_N}$ . By enlarging each ${B_N}$ as necessary we may assume that the ${B_N}$ are increasing in ${N}$ . The decreasing nature of the ${F_N}$ then gives the inclusions

$\displaystyle G_{N+1} \subset \pi_{B_N \leftarrow B_{N+1}}^{-1}(G_N).$

By inner regularity, one can find a compact subset ${K_N}$ of each ${G_N}$ such that

$\displaystyle \mu_{B_N}(K_N) \geq \mu_{B_N}(G_N) - \varepsilon/2^{N+1}.$

If we then set

$\displaystyle K'_N := \bigcap_{N'=1}^N \pi_{B_{N'} \leftarrow B_N}^{-1}( K_{N'} )$

then we see that each ${K'_N}$ is compact and

$\displaystyle \mu_{B_N}(K'_N) \geq \mu_{B_N}(G_N) - \sum_{N'=1}^N \varepsilon/2^{N'+1} \geq \varepsilon - \varepsilon/2.$

In particular, the sets ${K'_N}$ are non-empty. By construction, we also have the inclusions

$\displaystyle K'_{N+1} \subset \pi_{B_N \leftarrow B_{N+1}}^{-1}(K'_N)$

and thus the sets ${H_N := \pi_{B_N}^{-1}(K'_N)}$ are decreasing in ${N}$ . On the other hand, since these sets are contained in ${F_N}$ , we have ${\bigcap_{N=1}^\infty H_N = \emptyset}$ .
By the axiom of choice, we can select an element ${x_N \in H_N}$ from ${H_N}$ for each ${N}$ . Observe that for any ${N_0}$ , that ${\pi_{B_{N_0}}(x_N)}$ will lie in the compact set ${K'_{N_0}}$ whenever ${N \geq N_0}$ . Applying the Heine-Borel theorem repeatedly, we may thus find a subsequence ${x_{N_{1,m}}}$ of the ${x_N}$ for ${m=1,2,\ldots}$ such that ${\pi_{B_1}(x_{N_{1,m}})}$ converges; then we can find a further subsequence ${x_{N_{2,m}}}$ of that subsequence such that ${\pi_{B_2}(x_{N_{2,m}})}$ , and more generally obtain nested subsequences ${x_{N_{j,m}}}$ for ${m=1,2,\ldots}$ and ${j=1,2,\ldots}$ such that for each ${j=1,2,\ldots}$ , the sequence ${m \mapsto \pi_{B_j}(x_{N_{j,m}})}$ converges.
Now we use the diagonalisation trick. Consier the sequence ${x_{N_{m,m}} =: (y_{m,\alpha})_{\alpha \in A}}$ for ${m=1,2,\ldots}$ . By construction, we see that for each ${j}$ , ${\pi_{B_j}(x_{N_{m,m}})}$ converges to a limit as ${m \rightarrow \infty}$ . This implies that for each ${\alpha \in \bigcup_{j=1}^\infty B_j}$ , ${y_{m,\alpha}}$ converges to a limit ${y_\alpha}$ as ${m \rightarrow \infty}$ . As ${K'_j}$ is closed, we see that ${(y_\alpha)_{\alpha \in B_j} \in K'_j}$ for each ${j}$ . If we then extend ${y_\alpha}$ arbitrarily from ${\alpha \in \bigcup_{j=1}^\infty B_j}$ to ${\alpha \in A}$ , then the point ${y := (y_\alpha)_{\alpha \in A}}$ lies in ${H_j}$ for each ${j}$ . But this contradicts the fact that ${\bigcap_{N=1}^\infty H_N=\emptyset}$ . This contradiction completes the proof that ${\mu_0}$ is a pre-measure.
If we then let ${\mu}$ be the Hahn-Kolmogorov extension of ${\mu_0}$ , one easily verifies that ${\mu}$ obeys all the required properties, and the uniqueness follows from Exercise 15. $\Box$
The Kolmogorov extension theorem is a fundamental tool in the foundations of probability theory, as it allows one to construct a probability space to hold a variety of random processes ${(X_t)_{t \in T}}$ , both in the discrete case (when the set of times ${T}$ is something like the integers ${{\bf Z}}$ ) and in the continuous case (when the set of times ${T}$ is something like ${{\bf R}}$ ). In particular, it can be used to rigorously construct a process for Brownian motion, known as the Wiener process. We will however not focus on this topic, which can be found in many graduate probability texts. But we will give one common special case of the Kolmogorov extension theorem, which is to construct product probability measures:

Theorem 63 (Existence of product measures) Let ${A}$ be an arbitrary set. For each ${\alpha \in A}$ , let ${(X_\alpha,{\mathcal B}_\alpha,\mu_\alpha)}$ be a probability space in which ${X_\alpha}$ is a locally compact, ${\sigma}$ -compact metric space, with ${{\mathcal B}_\alpha}$ being its Borel ${\sigma}$ -algebra (i.e. the ${\sigma}$ -algebra generated by the open sets). Then there exists a unique probability measure ${\mu_A = \prod_{\alpha \in A} \mu_\alpha}$ on ${(X_A,{\mathcal B}_A) := (\prod_{\alpha \in A} X_\alpha, \prod_{\alpha \in A} {\mathcal B}_\alpha)}$ with the property that

$\displaystyle \mu_A( \prod_{\alpha \in A} E_\alpha ) = \prod_{\alpha \in A} \mu_\alpha(E_\alpha)$

whenever ${E_\alpha \in {\mathcal B}_\alpha}$ for each ${\alpha \in A}$ , and one has ${E_\alpha=X_\alpha}$ for all but finitely many of the ${\alpha}$ .

Proof: We apply the Kolmogorov extension theorem to the finite product measures ${\mu_B := \prod_{\alpha \in B} \mu_\alpha}$ for finite ${B \subset A}$ , which can be constructed using the machinery in Section 4. These are Borel probability measures on a locally compact, ${\sigma}$ -compact space and are thus inner regular by Exercise 12 of 245B Notes 12. The compatibility condition (13) can be verified from the uniqueness properties of finite product measures. $\Box$

Remark 64 This result can also be obtained from the }{Riesz representation theorem}, which we will cover in 245B Notes 12.

Example 65 (Bernoulli cube) Let ${A := {\bf N}}$ , and for each ${\alpha \in A}$ , let ${(X_\alpha,{\mathcal B}_\alpha,\mu_\alpha)}$ be the two-element set ${X_\alpha = \{0,1\}}$ with the discrete metric (and thus discrete ${\sigma}$ -algebra) and the uniform probability measure ${\mu_\alpha}$ . Then Theorem 63 gives a probability measure ${\mu}$ on the infinite discrete cube ${X_A := \{0,1\}^{\bf N}}$ , known as the (uniform) Bernoulli measure on this cube. The coordinate functions ${\pi_\alpha: X_A \rightarrow \{0,1\}}$ can then be interpreted as a countable sequence of random variables taking values in ${\{0,1\}}$ . From the properties of product measure one can easily check that these random variables are uniformly distributed on ${\{0,1\}}$ and are jointly independent. Informally, Bernoulli measure allows one to model an infinite number of “coin flips”. One can replace the natural numbers here by any other index set, and have a similar construction.

Example 66 (Continuous cube) We repeat the previous example, but replace ${\{0,1\}}$ with the unit interval ${[0,1]}$ (with the usual metric, the Borel ${\sigma}$ -algebra, and the uniform probability measure). This gives a probability measure on the infinite continuous cube ${[0,1]^{\bf N}}$ , and the coordinate functions ${\pi_\alpha: X_A \rightarrow [0,1]}$ can now be interpreted as jointly independent random variables, each having the uniform distribution on ${[0,1]}$ .

Example 67 (Independent gaussians) We repeat the previous example, but now replace ${[0,1]}$ with ${{\bf R}}$ (with the usual metric, and the Borel ${\sigma}$ -algebra), and the normal probability distribution ${d\mu_\alpha = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}\ dx}$ (thus ${\mu_\alpha(E) = \int_E \frac{1}{\sqrt{2\pi}} e^{-x^2/2}\ dx}$ for every Borel set ${E}$ ). This gives a probability space that supports a countable sequence of jointly independent gaussian random variables ${\pi_\alpha}$ .

84 comments

Comments feed for this article

21 April, 2018 at 3:10 am

Anonymous

For lemma 35,

Correct me if I am wrong, but is the second paragraph necessary: “It is also clear… closed under complements. ” As $X \in A$ , the proof already shows $D$ is closed under complements, $X\backslash B=B^c$ .

21 April, 2018 at 7:57 am

Terence Tao

Yes, one could arrange the argument in this fashion instead if one wished.

3 October, 2018 at 6:00 am

Nathanael Schilling

I think there is a small mistake in the proof of the Kolomogorov Extension Theorem (Theorem 62) Here you write:

$\displaystyle \mu_{B_N}(K'_N) \geq \mu_{B_N}(G_N) - \varepsilon/2^N \geq \varepsilon - \varepsilon/2^N$ .

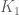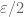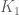As $K_1$ potentially only has measure $\varepsilon/2$ , and hence $K'_N$ (which is contained in the inverse image under a projection of $K_1$ ) cannot have a larger measure.

[Corrected, thanks – T.]

22 January, 2021 at 6:22 am

Anonymous

Dear Professor Tao

Can I ask you about the following thing, please?:In (4) of Exercise 59. How can we get the at most countable set {B} and get the function {f_B}?
Now I just know that if want that {f = f_B \circ \pi_B},we will have that
{ (x_\alpha)_{\alpha \in A}} and { (x^’_\alpha)_{\alpha \in A}}are equal under the given function {f} if {x_\alpha = x^’_\alpha} for all {\alpha belong B}.

22 January, 2021 at 1:22 pm

Anonymous

In theorem 18, it seems that there is a typo in the definition of left and right limits of $F$ .

[Corrected, thanks – T.]

11 October, 2021 at 9:19 am

254A, Supplement 4: Probabilistic models and heuristics for the primes (optional) | What's new

[…] of random variables, as this set of notes is not focused on rigorous formalism. (See for instance this previous post for the relevant theory […]

30 April, 2022 at 12:52 am

Outer Measures – deep mind

[…] Apart from the literature [1] to [6] listed at the end of this post, we also refer to the lecture 245A notes of T. Tao. […]

	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on 275A, Notes 3: The weak and st…
	Anonymous on It ought to be common knowledg…
	Ring Theory Intervie… on Reading seminar: “Stable…
	Anonymous on Work hard
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Erratum for “An inverse…
	Anonymous on Erratum for “An inverse…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…
	Anonymous on Infinite partial sumsets in th…

245A, Notes 6: Outer measures, pre-measures, and product measures

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

84 comments

Leave a comment Cancel reply

For commenters

245A, Notes 6: Outer measures, pre-measures, and product measures

Share this:

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

84 comments

Leave a comment Cancel reply

For commenters