Let be a compact group. (Throughout this post, all topological groups are assumed to be Hausdorff.) Then
has a number of unitary representations, i.e. continuous homomorphisms
to the group
of unitary operators on a Hilbert space
, equipped with the strong operator topology. In particular, one has the left-regular representation
, where we equip
with its normalised Haar measure
(and the Borel
-algebra) to form the Hilbert space
, and
is the translation operation
We call two unitary representations and
isomorphic if one has
for some unitary transformation
, in which case we write
.
Given two unitary representations and
, one can form their direct sum
in the obvious manner:
. Conversely, if a unitary representation
has a closed invariant subspace
of
(thus
for all
), then the orthogonal complement
is also invariant, leading to a decomposition
of
into the subrepresentations
,
. Accordingly, we will call a unitary representation
irreducible if
is nontrivial (i.e.
) and there are no nontrivial invariant subspaces (i.e. no invariant subspaces other than
and
); the irreducible representations play a role in the subject analogous to those of prime numbers in multiplicative number theory. By the principle of infinite descent, every finite-dimensional unitary representation is then expressible (perhaps non-uniquely) as the direct sum of irreducible representations.
The Peter-Weyl theorem asserts, among other things, that the same claim is true for the regular representation:
Theorem 1 (Peter-Weyl theorem) Let
be a compact group. Then the regular representation
is isomorphic to the direct sum of irreducible representations. In fact, one has
, where
is an enumeration of the irreducible finite-dimensional unitary representations
of
(up to isomorphism). (It is not difficult to see that such an enumeration exists.)
In the case when is abelian, the Peter-Weyl theorem is a consequence of the Plancherel theorem; in that case, the irreducible representations are all one dimensional, and are thus indexed by the space
of characters
(i.e. continuous homomorphisms into the unit circle
), known as the Pontryagin dual of
. (See for instance my lecture notes on the Fourier transform.) Conversely, the Peter-Weyl theorem can be used to deduce the Plancherel theorem for compact groups, as well as other basic results in Fourier analysis on these groups, such as the Fourier inversion formula.
Because the regular representation is faithful (i.e. injective), a corollary of the Peter-Weyl theorem (and a classical theorem of Cartan) is that every compact group can be expressed as the inverse limit of Lie groups, leading to a solution to Hilbert’s fifth problem in the compact case. Furthermore, the compact case is then an important building block in the more general theory surrounding Hilbert’s fifth problem, and in particular a result of Yamabe that any locally compact group contains an open subgroup that is the inverse limit of Lie groups.
I’ve recently become interested in the theory around Hilbert’s fifth problem, due to the existence of a correspondence principle between locally compact groups and approximate groups, which play a fundamental role in arithmetic combinatorics. I hope to elaborate upon this correspondence in a subsequent post, but I will mention that versions of this principle play a crucial role in Gromov’s proof of his theorem on groups of polynomial growth (discussed previously on this blog), and in a more recent paper of Hrushovski on approximate groups (also discussed previously). It is also analogous in many ways to the more well-known Furstenberg correspondence principle between ergodic theory and combinatorics (also discussed previously).
Because of the above motivation, I have decided to write some notes on how the Peter-Weyl theorem is proven. This is utterly standard stuff in abstract harmonic analysis; these notes are primarily for my own benefit, but perhaps they may be of interest to some readers also.
— 1. Proof of the Peter-Weyl theorem —
Throughout these notes, is a fixed compact group.
Let and
be unitary representations. An (linear) equivariant map
is defined to be a continuous linear transformation such that
for all
.
A fundamental fact in representation theory, known as Schur’s lemma, asserts (roughly speaking) that equivariant maps cannot mix irreducible representations together unless they are isomorphic. More precisely:
Lemma 2 (Schur’s lemma for unitary representations) Suppose that
and
are irreducible unitary representations, and let
be an equivariant map. Then
is either the zero transformation, or a constant multiple of an isomorphism. In particular, if
, then there are no non-trivial equivariant maps between
and
.
Proof: The adjoint map of the equivariant map
is also equivariant, and thus so is
. As
is also a bounded self-adjoint operator, we can apply the spectral theorem to it. Observe that any closed invariant space of
is
-invariant, and is thus either
or
. By the spectral theorem, this forces
to be a constant multiple of the identity. Similarly for
. This forces
to either be zero or a constant multiple of a unitary map, and the claim follows. (Thanks to Frederick Goodman for this proof.)
Schur’s lemma has many foundational applications in the subject. For instance, we have the following generalisation of the well-known fact that eigenvectors of a unitary operator with distinct eigenvalues are necessarily orthogonal:
Corollary 3 Let
and
be two irreducible subrepresentations of a unitary representation
. Then one either has
or
.
Proof: Apply Schur’s lemma to the orthogonal projection from to
.
Another application shows that finite-dimensional linear representations can be canonically identified (up to constants) with finite-dimensional unitary representations:
Corollary 4 Let
be a linear representation on a finite-dimensional space
. Then there exists a Hermitian inner product
on
that makes this representation unitary. Furthermore, if
is irreducible, then this inner product is unique up to constants.
Proof: To show existence of the Hermitian inner product that unitarises , take an arbitrary Hermitian inner product
and then form the average
(this is the “Weyl averaging trick”, which crucially exploits compactness of ). Then one easily checks (using the fact that
is finite dimensional and thus locally compact) that
is also Hermitian, and that
is unitary with respect to this inner product, as desired. (This part of the argument does not use finite dimensionality.)
To show uniqueness up to constants, assume that one has two such inner products ,
on
, and apply Schur’s lemma to the identity map between the two Hilbert spaces
and
. (Here, finite dimensionality is used to establish
A third application of Schur’s lemma allows us to express the trace of a linear operator as an average:
Corollary 5 Let
be an irreducible unitary representation on a non-trivial finite-dimensional space
, and let
be a linear transformation. Then
where
is the identity operator.
Proof: The right-hand side is equivariant, and hence by Schur’s lemma is a multiple of the identity. Taking traces, we see that the right-hand side also has the same trace as . The claim follows.
Let us now consider the irreducible subrepresentations of the left-regular representation
. From Corollary 3, we know that those subrepresentations coming from different isomorphism classes in
are orthogonal, so we now focus attention on those subrepresentations coming from a single class
. Define the
-isotypic component
of the regular representation to be the finite-dimensional subspace of
spanned by the functions of the form
where are arbitrary vectors in
. This is clearly a left-invariant subspace of
(in fact, it is bi-invariant, a point which we will return to later), and thus induces a subrepresentation of the left-regular representation. In fact, it captures precisely all the subrepresentations of the left-regular representation that are isomorphic to
:
Proposition 6 Let
. Then every irreducible subrepresentation
of the left-regular representation
that is isomorphic to
is a subrepresentation of
. Conversely,
is isomorphic to the direct sum
of
copies of
. (In particular,
has dimension
).
Proof: Let be a subrepresentation of the left-regular representation that is isomorphic to
. Thus, we have an equivariant isometry
whose image is
; it has an adjoint
.
Let and
. The convolution
can be re-arranged as
where
In particular, we see that for every
. Letting
be a sequence (or net) of approximations to the identity, we conclude that
as well, and so
, which is the first claim.
To prove the converse claim, write , and let
be an orthonormal basis for
. Observe that we may then decompose
as the direct sum of the spaces
for . The claim follows.
From Corollary 3, the -isotypic components
for
are pairwise orthogonal, and so we can form the direct sum
, which is an invariant subspace of
that contains all the finite-dimensional irreducible subrepresentations (and hence also all the finite-dimensional representations, period). The essence of the Peter-Weyl theorem is then the assertion that this direct sum in fact occupies all of
:
Proposition 7 We have
.
Proof: Suppose this is not the case. Taking orthogonal complements, we conclude that there exists a non-trivial which is orthogonal to all
, and is in particular orthogonal to all finite-dimensional subrepresentations of
.
Now let be an arbitrary self-adjoint kernel, thus
for all
. The convolution operator
is then a self-adjoint Hilbert-Schmidt operator and is thus compact. (Here, we have crucially used the compactness of
.) By the spectral theorem, the cokernel
of this operator then splits as the direct sum of finite-dimensional eigenspaces. As
is equivariant, all these eigenspaces are invariant, and thus orthogonal to
; thus
must lie in the kernel of
, and thus
vanishes for all self-adjoint
. Using a sequence (or net) of approximations to the identity, we conclude that
vanishes also, a contradiction.
Theorem 1 follows by combining this proposition with 6.
— 2. Nonabelian Fourier analysis —
Given , the space
of linear transformations from
to
is a finite-dimensional Hilbert space, with the Hilbert-Schmidt inner product
; it has a unitary action of
as defined by
. For any
, the function
can be easily seen to lie in
, giving rise to a map
. It is easy to see that this map is equivariant.
Proof: As and
are finite-dimensional spaces with the same dimension
, it suffices to show that this map is an isometry, thus we need to show that
for all . By bilinearity, we may reduce to the case when
are rank one operators
for some , where
is the dual vector
to
, and similarly for
. Then we have
and
The latter expression can be rewritten as
Applying Fubini’s theorem, followed by Corollary 5, this simplifies to
which simplifies to , and the claim follows.
As a corollary of the above proposition, the orthogonal projection of a function to
can be expressed as
We call
the Fourier coefficient of at
, thus the projection of
to
is the function
which has an norm of
. From the Peter-Weyl theorem we thus obtain the Fourier inversion formula
and the Plancherel identity
We can write these identities more compactly as an isomorphism
where the dilation of a Hilbert space
is formed by using the inner product
. This is an isomorphism not only of Hilbert spaces, but of the left-action of
. Indeed, it is an isomorphism of the bi-action of
on both the left and right of both
and
, defined by
and
It is easy to see that each of the are irreducible with respect to the
action. Indeed, first observe from Proposition 8 that
is surjective, and thus
must span all of
. Thus, any bi-invariant subspace of
must also be invariant with respect to left and right multiplication by arbitrary elements of
, and in particular by rank one operators; from this one easily sees that there are no non-trivial bi-invariant subspaces. Thus we can view the Peter-Weyl theorem as also describing the irreducible decomposition of
into
-irreducible components.
Remark 9 In view of (1), it is natural to view
as being the “spectrum” of
, with each “frequency”
occuring with “multiplicity”
.
In the abelian case, any eigenspace of one unitary operator is automatically an invariant subspace of all other
, which quickly implies (from the spectral theorem) that all irreducible finite-dimensional unitary representations must be one-dimensional, in which case we see that the above formulae collapse to the usual Fourier inversion and Plancherel theorems for compact abelian groups.
In the case of a finite group , we can take dimensions in (1) to obtain the identity
In the finite abelian case, we see in particular that and
have the same cardinality.
Direct computation also shows other basic Fourier identities, such as the convolution identity
for , thus partially diagonalising convolution into multiplication of linear operators on finite-dimensional vector spaces
. (Of course, one cannot expect complete diagonalisation in the non-abelian case, since convolution would then also be non-abelian, whereas diagonalised operators must always commute with each other.)
Call a function a class function if it is conjugation-invariant, thus
for all
. It is easy to see that this is equivalent to each of the Fourier coefficients
also being conjugation-invariant:
. By Lemma 5, this is in turn equivalent to
being equal to a multiple of the identity:
where the character of the representation
is given by the formula
The Plancherel identity then simplifies to
thus the form an orthonormal basis for the space
of class functions. Analogously to (1), we have
(In particular, in the case of finite groups ,
has the same cardinality as the space of conjugacy classes of
.)
Characters are a fundamentally important tool in analysing finite-dimensional representations of
that are not necessarily irreducible; indeed, if
decomposes into irreducibles as
, then the character
then similarly splits as
and so the multiplicities of each component
in
can be given by the formula
In particular, these multiplicities are unique: all decompositions of into irreducibles have the same multiplicities.
Remark 10 Representation theory becomes much more complicated once one leaves the compact case; convolution operators
are no longer compact, and can now admit continuous spectrum in addition to pure point spectrum. Furthermore, even when one has pure point spectrum, the eigenspaces can now be infinite dimensional. Thus, one must now grapple with infinite-dimensional irreducible representations, as well as continuous combinations of representations that cannot be readily resolved into irreducible components. Nevertheless, in the important case of locally compact groups, it is still the case that there are “enough” irreducible unitary representations to recover a significant portion of the above theory. The fundamental theorem here is the Gelfand-Raikov theorem, which asserts that given any non-trivial group element
in a locally compact group, there exists a irreducible unitary representation (possibly infinite-dimensional) on which
acts non-trivially. Very roughly speaking, this theorem is first proven by observing that
acts non-trivially on the regular representation, which (by the Gelfand-Naimark-Segal (GNS) construction) gives a state on the *-algebra of measures on
that distinguishes the Dirac mass
at
from the Dirac mass
from the origin. Applying the Krein-Milman theorem, one then finds an extreme state with this property; applying the GNS construction, one then obtains the desired irreducible representation.

28 comments
Comments feed for this article
23 January, 2011 at 2:21 pm
Allen Knutson
I do not understand why one ever states Peter-Weyl as an isomorphism of G-reps, rather than GxG-reps, where the isotypic components are actually irreducible. (That’s a good place to stop, though I suppose one could move on to the wreath product.) And yet I almost never see it presented as a GxG-theorem.
24 January, 2011 at 4:16 am
Terence Tao
Yes, I remember you emphasising this point to me way back in grad school :-). I think that in most applications, one either needs only the G-rep version, or else one may as well go all the way to the nonabelian Fourier inversion formula. The fact that the xi-isotypic components are GxG irreducible is nice, but I don’t know of many places where this fact is actually used very much.
7 January, 2012 at 12:10 pm
Robert Donley
One step back from Peter-Weyl are the non-vanishing Schur Orthogonality Relations. The irreducible GxG-type $V\otimes V^*$ is the matrix coefficient span for V, and the tensor is unitary for GxG if the G-rep is unitary. We have two GxG-invariant inner products: one on tensors, and one on matrix coefficients.
From there, the SORs follow from Schur’s Lemma for GxG. We can think of biinvariant integration as an intertwinor of unique trivial GxG-types.
This scenario can be posed without compactness, square integrability, or even unitarity. The question becomes: what takes the place of invariant integration in the SORs? Midorikawa answers this for some classes of tempered unitary reps on semisimple Lie groups, but the general case is wide open.
24 January, 2011 at 9:37 am
Allen Knutson
I don’t understand why you portray the nonabelian Fourier inversion formula as being further than the GxG-version, insofar as it still has a “dim(V)” factor in it.
There are other statements of the form “ acts on X, such that Fun(X) is a sum of
acts on X, such that Fun(X) is a sum of  , where neither the
, where neither the  nor
nor 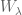 repeat. For example,
repeat. For example,  acting on
acting on  . I don’t know a uniform statement that would include Peter-Weyl, but wouldn’t be surprised if there is one.
. I don’t know a uniform statement that would include Peter-Weyl, but wouldn’t be surprised if there is one.
24 January, 2011 at 3:49 pm
Terence Tao
Well, the dim(V) factor is now only in the normalisation of the inner product, rather than in the Cartesian exponent.
Here’s roughly how I see the three facts:
G-rep Peter-Weyl: as
as  -vector spaces, with no canonical identification.
-vector spaces, with no canonical identification.
Fourier inversion: as
as  –Hilbert spaces, with identification given by the Fourier transform.
–Hilbert spaces, with identification given by the Fourier transform.
Note that the Fourier map from
from 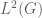 to
to  (or
(or 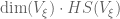 ) is already
) is already  -equivariant, so the Fourier transform is providing the canonical decomposition of
-equivariant, so the Fourier transform is providing the canonical decomposition of 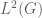 into
into  -isotypic components.
-isotypic components.
As I see it, the main thing that the -rep version of Peter-Weyl brings to the table beyond the Fourier inversion formula is the
-rep version of Peter-Weyl brings to the table beyond the Fourier inversion formula is the  -irreducibility of the components, which in the vector space category are
-irreducibility of the components, which in the vector space category are  and in the Hilbert space category are
and in the Hilbert space category are 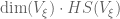 . This irreducibility can be deduced from the inversion formula (as I do above) but I don’t know of many situations where one would need to use it, and for which one could not easily substitute the inversion formula in its place instead.
. This irreducibility can be deduced from the inversion formula (as I do above) but I don’t know of many situations where one would need to use it, and for which one could not easily substitute the inversion formula in its place instead.
24 January, 2011 at 8:19 pm
David Ben-Zvi
One thing that the version adds (that I also learned from Allen in grad school!) is that it encodes simultaneously the harmonic analysis for all homogeneous spaces for
version adds (that I also learned from Allen in grad school!) is that it encodes simultaneously the harmonic analysis for all homogeneous spaces for  : for
: for 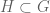 we can describe functions on
we can describe functions on 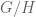 (by taking
(by taking  -invariants on one side in Peter-Weyl) as the sum of irreps of
-invariants on one side in Peter-Weyl) as the sum of irreps of  with multiplicity spaces given by the
with multiplicity spaces given by the  -invariants on their duals.
-invariants on their duals.
This might be even more useful in the complexified form of Peter-Weyl (as decomposing regular functions on the complex group ): a great example of this is to take the maximal nilpotent
): a great example of this is to take the maximal nilpotent  , which by the theorem of highest weight has a unique invariant (up to scale) on any irrep, so we recover that
, which by the theorem of highest weight has a unique invariant (up to scale) on any irrep, so we recover that  is a “model space” for
is a “model space” for  , with functions given by the sum of all irreps with multiplicity one, labeled by highest weights (the torus action on this line of invariants) – this is a restatement of Borel-Weil.
, with functions given by the sum of all irreps with multiplicity one, labeled by highest weights (the torus action on this line of invariants) – this is a restatement of Borel-Weil.
7 March, 2011 at 7:58 am
David Speyer
Here is a neat example I just ran across where the version gets you something that the
version gets you something that the  -version doesn’t.
-version doesn’t.
Suppose we want to compute the deRham cohomology of a compact Lie group.
If we only keep track of one -action, the
-action, the  -forms are
-forms are 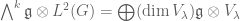 . It is not obvious that this has any cohomology at all: The dimensions are completely consistent with the complex being exact. For example, if we are looking at
. It is not obvious that this has any cohomology at all: The dimensions are completely consistent with the complex being exact. For example, if we are looking at  , and we label a representation by the generating function of its highest weight vectors, then we are dealing with
, and we label a representation by the generating function of its highest weight vectors, then we are dealing with
Now, suppose we keep track of the action. Then it turns out that the multiplicity of
action. Then it turns out that the multiplicity of 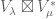 in
in 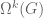 is
is  . For example, when you look at
. For example, when you look at  , you get
, you get
Now it is obvious that we get cohomology in degrees and
and  : There is no place for the trivial terms to go! And, if you recall that the
: There is no place for the trivial terms to go! And, if you recall that the  -action on
-action on 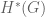 is trivial, it is obvious that all the other terms are exact.
is trivial, it is obvious that all the other terms are exact.
14 May, 2011 at 12:54 pm
Joel Moreira
In the proof of proposition 6, is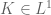 (instead of L^2) a typo or there is a reason I don’t see?
(instead of L^2) a typo or there is a reason I don’t see? should be
should be 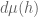 .
.
Also I think the
Thank you
[Corrected, thanks – T.]
30 May, 2011 at 4:39 pm
van Dantzig’s theorem « What’s new
[…] (for instance, one can start analysing them using the Peter-Weyl theorem, as discussed in this previous post). The global behaviour however remains more complicated, in part because the compact open subgroup […]
31 May, 2011 at 6:33 pm
Laplace算子与表示论 « Fight with Infinity
[…] Tao The Peter-Weyl theorem, and non-abelian Fourier analysis on compact groups […]
17 June, 2011 at 2:15 pm
Hilbert’s fifth problem and Gleason metrics « What’s new
[…] Theorem 5 and Theorem 6 proceed by some elementary combinatorial analysis, together with the use of Haar measure (to build convolutions, and thence to build “smooth” bump functions with which to create a metric, in a variant of the analysis used to prove the Birkhoff-Kakutani theorem); Theorem 5 also requires Peter-Weyl theorem (to dispose of certain compact subgroups that arise en route to the reduction to the NSS case), which was discussed previously on this blog. […]
27 September, 2011 at 3:30 pm
254A, Notes 3: Haar measure and the Peter-Weyl theorem « What’s new
[…] sharpest form of the theorem, as it only describes the left -action and not the right -action; see this previous blog post for a precise statement and proof of the Peter-Weyl theorem in its strongest form. This form is of […]
16 December, 2011 at 10:14 am
254B, Notes 3: Quasirandom groups, expansion, and Selberg’s 3/16 theorem « What’s new
[…] (which is based on the Peter-Weyl theorem combined with Schur’s lemma, and is developed in this blog post); we leave this as an exercise for the interested reader. Exercise 10 Let be subsets of a […]
16 December, 2011 at 10:50 am
254B, Notes 3: Quasirandom groups, expansion, and Selberg’s 3/16 theorem | t1u
[…] (which is based on the Peter-Weyl theorem combined with Schur’s lemma, and is developed in this blog post); we leave this as an exercise for the interested […]
5 December, 2013 at 7:41 pm
benbrawn
Hi Terry,
in the statement of Theorem 1 (Peter-Weyl theorem), I think the \oplus in the exponent is a typo. Maybe?
5 December, 2013 at 8:19 pm
Terence Tao
No; I use to denote the direct sum of
to denote the direct sum of  copies of
copies of 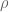 (and
(and  to denote the tensor product of
to denote the tensor product of  copies of
copies of 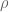 ).
).
11 January, 2014 at 6:21 am
Draft notes | alexchervov
[…] https://terrytao.wordpress.com/2011/01/23/the-peter-weyl-theorem-and-non-abelian-fourier-analysis-on-… […]
22 September, 2018 at 2:36 am
Group limits – Random Permutations
[…] We borrow nonabelian harmonic analysis notation from Tao. Certainly we may assume that and are internal, say and . Then by nonabelian […]
4 July, 2019 at 10:55 pm
Frederik vom Ende
Dear Prof. Tao, thank you for this comprehensive and nice blog entry! At the beginning of section 2 you write that “ can be easily seen to lie in
can be easily seen to lie in 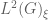 “. But—also after checking with some further literature—it seems to me that
“. But—also after checking with some further literature—it seems to me that  should be correct here (or is it evident that maps of the form
should be correct here (or is it evident that maps of the form  also lie in the subspace
also lie in the subspace  ? This of course would not change anything substantial about the follow-up statements and proofs aside from handing out a few extra
? This of course would not change anything substantial about the follow-up statements and proofs aside from handing out a few extra  . Kind regards
. Kind regards
[Corrected, thanks – T.]
19 April, 2020 at 4:15 am
Amin
Dear Professor Tao,
Are you sure that with your convention of Fourier inverse i_ξ , it entertwinnes (L,R) with the action on operators as you defined? I think it works when the Fourier inverse maps T in HS(V_ξ ) to the function on G : Tr(T ξ(g^(-1) ) .
Best Regards
19 April, 2020 at 11:51 am
Terence Tao
Can you be more precise (e.g., by pointing out a specific line in the blog post that may require clarification or correction)?
19 April, 2020 at 11:48 pm
Amin
Yes, it is in the part on non abelian Fourier analysis, after equation 1 :
“This is an isomorphism not only of Hilbert spaces, but of the left-action of {G}. Indeed, it is an isomorphism of the bi-action of {G \times G} on both the left and right of both {L^2(G)} and {HS(V_\xi)}, defined by…”
I suppose, after now looking at the comment of F. Vom Ende, that it is due to a change that you made in the function on G that you associate to an operator on a representation space (the i_ξ).
It’s a minor point anyway, and more importantly, thank you for sharing your insights on your blog.
[Action should be fixed now, thanks – T.>]
30 May, 2020 at 1:30 am
Leon
Dear Prof. Tao,
thank you for this helpful right-up! I have two questions on Lemma 2, Schur’s Lemma for unitary representations:
1.: “Observe that any closed invariant subspace of {T^* T} is {G}-invariant”
How can we see this? If {X} is closed and invariant under {T^* T} and we look at {g \in G}, we can deduce that {\rho(g)X} is closed and invariant under {T^* T} as well, but I don’t see how this helps us in showing that it is a subset of {X}. Am I missing something?
2.: Does this Lemma also work if we look at representations over the real numbers, instead of the complex numbers, and replace “unitary” by “orthogonal”? After all, the constant multiple seems to be a real number, and I don’t see what else might go wrong.
30 May, 2020 at 8:17 pm
Terence Tao
Sorry. “invariant subspace” should be “eigenspace” here. The problem in the real case is that eigenspaces can be complex even when the operators are real and orthogonal (consider for instance a rotation matrix).
31 May, 2020 at 7:05 am
Leon
Dear Prof. Tao,
thank you for the correction!
In the real case, since we’re considering self-adjoint operators I don’t see the problem you’re stating. Assume for simplicity that we already knew that all irreducible representations were finite-dimensional. Then is self-adjoint, i.e. symmetric, and thus diagonalizable over
is self-adjoint, i.e. symmetric, and thus diagonalizable over 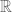 . Can’t we proceed from there as in your proof and obtain the same result?
. Can’t we proceed from there as in your proof and obtain the same result?
In general, I’m wondering how far we can take this and what goes wrong about Peter-Weyl in the real case. As far as I can see, the only thing that goes wrong is that we can’t conclude that the multiplicity of each irreducible representation equals its dimension, but the basic decomposition of the regular representation into irreducible representations should hold.
Best wishes,
Leon
1 June, 2020 at 2:01 pm
Terence Tao
Ah, I see now where things are hiding. Lemma 2 is true in the real case as well, but when applied to equivariant maps of an irrep to itself only gives an orthogonal map on
to itself only gives an orthogonal map on  , not a constant multiple of the identity. In the complex case the only unitary equivariant maps on
, not a constant multiple of the identity. In the complex case the only unitary equivariant maps on  are multiples of the identity because of the spectral theorem (any non-trivial eigenspace would break irreducibility), but in the real case one can have non-trivial orthogonal equivariant maps (e.g. consider the tautological orthogonal rep of
are multiples of the identity because of the spectral theorem (any non-trivial eigenspace would break irreducibility), but in the real case one can have non-trivial orthogonal equivariant maps (e.g. consider the tautological orthogonal rep of 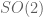 on
on 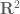 , which is irreducible but has all the rotations as equivariant orthogonal maps).
, which is irreducible but has all the rotations as equivariant orthogonal maps).
8 October, 2020 at 10:43 am
Anonymous
I think there’s still something wrong with your proof of Schur’s lemma (Lemma 2). Why do you speak of eigenspaces? It may happen that a bounded linear operator on a Hilbert space has no eigenvalues (so no eigenspaces), but is not a constant multiple of the identity.
I think you rather mean spectral subspaces, and the argument may be like this: suppose that the spectrum of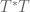 is not a point, then it can be decomposed as a union of two non-empty Borel subsets. Consider the orthogonal projector
is not a point, then it can be decomposed as a union of two non-empty Borel subsets. Consider the orthogonal projector  onto the spectral subspace corresponding to one of them; it is a Borel function of
onto the spectral subspace corresponding to one of them; it is a Borel function of 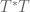 , so it commutes with all operators of the representation as well as
, so it commutes with all operators of the representation as well as 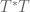 (because 1. polynomials in
(because 1. polynomials in 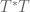 commute with the representation operators, 2. continuous functions can be approximated by polynomials, and 3. indicator functions can be approximated by continuous functions). Now this implies that the corresponding spectral subspace is
commute with the representation operators, 2. continuous functions can be approximated by polynomials, and 3. indicator functions can be approximated by continuous functions). Now this implies that the corresponding spectral subspace is  -invariant, so the representation is reducible.
-invariant, so the representation is reducible.
Or maybe I am missing something and there is a simpler proof?
[“Eigenspace” changed to “invariant space” – T.]
23 October, 2020 at 8:25 am
Leon Lang
Thanks again for the article!
It helped me to figure out a version of the Peter-Weyl Theorem for real representations (which has all the properties except that the multiplicity of the irreps can be smaller than their dimension).
We have used this to prove a “Wigner-Eckart Theorem” for equivariant convolution kernels in deep learning, which allows to parameterize these kernels for arbitrary compact groups and their homogeneous spaces:
https://arxiv.org/abs/2010.10952
Originally, the Wigner-Eckart Theorem is used to figure out the degrees of freedom of spherical tensor operators:
https://en.wikipedia.org/wiki/Wigner%E2%80%93Eckart_theorem