Recall that a (complex) abstract Lie algebra is a complex vector space (either finite or infinite dimensional) equipped with a bilinear antisymmetric form
that obeys the Jacobi identity
(One can of course define Lie algebras over other fields than the complex numbers , but in order to avoid some technical issues we shall work solely with the complex case in this post.)
An important special case of the abstract Lie algebras are the concrete Lie algebras, in which is a vector space of linear transformations
on a vector space
(which again can be either finite or infinite dimensional), and the bilinear form is given by the usual Lie bracket
It is easy to verify that every concrete Lie algebra is an abstract Lie algebra. In the converse direction, we have
Theorem 1 Every abstract Lie algebra is isomorphic to a concrete Lie algebra.
To prove this theorem, we introduce the useful algebraic tool of the universal enveloping algebra of the abstract Lie algebra
. This is the free (associative, complex) algebra generated by
(viewed as a complex vector space), subject to the constraints
This algebra is described by the Poincaré-Birkhoff-Witt theorem, which asserts that given an ordered basis of
as a vector space, that a basis of
is given by “monomials” of the form
where is a natural number, the
are an increasing sequence of indices in
, and the
are positive integers. Indeed, given two such monomials, one can express their product as a finite linear combination of further monomials of the form (3) after repeatedly applying (2) (which we rewrite as
) to reorder the terms in this product modulo lower order terms until one all monomials have their indices in the required increasing order. It is then a routine exercise in basic abstract algebra (using all the axioms of an abstract Lie algebra) to verify that this is multiplication rule on monomials does indeed define a complex associative algebra which has the universal properties required of the universal enveloping algebra.
The abstract Lie algebra acts on its universal enveloping algebra
by left-multiplication:
, thus giving a map from
to
. It is easy to verify that this map is a Lie algebra homomorphism (so this is indeed an action (or representation) of the Lie algebra), and this action is clearly faithful (i.e. the map from
to
is injective), since each element
of
maps the identity element
of
to a different element of
, namely
. Thus
is isomorphic to its image in
, proving Theorem 1.
In the converse direction, every representation of a Lie algebra “factors through” the universal enveloping algebra, in that it extends to an algebra homomorphism from
to
, which by abuse of notation we shall also call
.
One drawback of Theorem 1 is that the space that the concrete Lie algebra acts on will almost always be infinite-dimensional, even when the original Lie algebra
is finite-dimensional. However, there is a useful theorem of Ado that rectifies this:
Theorem 2 (Ado’s theorem) Every finite-dimensional abstract Lie algebra is isomorphic to a concrete Lie algebra over a finite-dimensional vector space
.
Among other things, this theorem can be used (in conjunction with the Baker-Campbell-Hausdorff formula) to show that every abstract (finite-dimensional) Lie group (or abstract local Lie group) is locally isomorphic to a linear group. (It is well-known, though, that abstract Lie groups are not necessarily globally isomorphic to a linear group, but we will not discuss these global obstructions here.)
Ado’s theorem is surprisingly tricky to prove in general, but some special cases are easy. For instance, one can try using the adjoint representation of
on itself, defined by the action
; the Jacobi identity (1) ensures that this indeed a representation of
. The kernel of this representation is the centre
. This already gives Ado’s theorem in the case when
is semisimple, in which case the center is trivial.
The adjoint representation does not suffice, by itself, to prove Ado’s theorem in the non-semisimple case. However, it does provide an important reduction in the proof, namely it reduces matters to showing that every finite-dimensional Lie algebra has a finite-dimensional representation
which is faithful on the centre
. Indeed, if one has such a representation, one can then take the direct sum of that representation with the adjoint representation to obtain a new finite-dimensional representation which is now faithful on all of
, which then gives Ado’s theorem for
.
It remains to find a finite-dimensional representation of which is faithful on the centre
. In the case when
is abelian, so that the centre
is all of
, this is again easy, because
then acts faithfully on
by the infinitesimal shear maps
. In matrix form, this representation identifies each
in this abelian Lie algebra with an “upper-triangular” matrix:
This construction gives a faithful finite-dimensional representation of the centre of any finite-dimensional Lie algebra. The standard proof of Ado’s theorem (which I believe dates back to work of Harish-Chandra) then proceeds by gradually “extending” this representation of the centre
to larger and larger sub-algebras of
, while preserving the finite-dimensionality of the representation and the faithfulness on
, until one obtains a representation on the entire Lie algebra
with the required properties. (For technical inductive reasons, one also needs to carry along an additional property of the representation, namely that it maps the nilradical to nilpotent elements, but we will discuss this technicality later.)
This procedure is a little tricky to execute in general, but becomes simpler in the nilpotent case, in which the lower central series becomes trivial for sufficiently large
:
Theorem 3 (Ado’s theorem for nilpotent Lie algebras) Let
be a finite-dimensional nilpotent Lie algebra. Then there exists a finite-dimensional faithful representation
of
. Furthermore, there exists a natural number
such that
, i.e. one has
for all
.
The second conclusion of Ado’s theorem here is useful for induction purposes. (By Engel’s theorem, this conclusion is also equivalent to the assertion that every element of is nilpotent, but we can prove Theorem 3 without explicitly invoking Engel’s theorem.)
Below the fold, I give a proof of Theorem 3, and then extend the argument to cover the full strength of Ado’s theorem. This is not a new argument – indeed, I am basing this particular presentation from the one in Fulton and Harris – but it was an instructive exercise for me to try to extract the proof of Ado’s theorem from the more general structural theory of Lie algebras (e.g. Engel’s theorem, Lie’s theorem, Levi decomposition, etc.) in which the result is usually placed. (However, the proof I know of still needs Engel’s theorem to establish the solvable case, and the Levi decomposition to then establish the general case.)
— 1. The nilpotent case —
We now prove Theorem 3. We achieve this by an induction on the dimension of . The claim is trivial for dimension zero, so we assume inductively that
has positive dimension, and that Theorem 3 has already been proven for all lower-dimensional nilpotent Lie algebras.
As noted earlier, the adjoint representation already verifies the claim except for the fact that it is not faithful on the centre . (The nilpotency of
ensures the existence of some
for which
.) Thus, it will suffice to find a finite-dimensional representation
that is faithful on the center
, and for which
for some
.
We have already verified the claim when is abelian (and can take
in this case), so suppose that
is not abelian; in particular, the centre
has strictly smaller dimension. We then observe that
must contain a codimension one ideal
containing
, which will of course again be a nilpotent Lie algebra. This can be seen by passing to the quotient
(which has positive dimension) and then to the abelianisation
(which still has positive dimension, by nilpotency), arbitrarily selecting a codimension one subspace of that abelianisation, and then passing back to
.
If we let be a one-dimensional complementary subspace of
, then
is automatically an abelian Lie algebra, and we have the decomposition
as vector spaces. This is not necessarily a direct sum of Lie algebras, though, because and
need not commute. However, as
is an ideal, we do know that
, thus there is an adjoint action
of
on
.
By induction hypothesis, we know that there is a faithful representation on some finite-dimensional space
with
for some
. We would like to somehow “extend” this representation to a finite-dimensional representation
which is still faithful on
(and hence on
), and with
for some
.
To motivate the construction, let us begin not with , but with the universal enveloping algebra representation
of
on
. The idea is to somehow combine this action
with an action of
on the same space
to obtain an action of the full Lie algebra
on
. To do this, recall that we have the adjoint action
of
on
. This extends to an adjoint action of
on
, defined by the Leibniz rule
one can easily verify that this is indeed an action (and furthermore that the map is a derivation on
). One can then combine the multiplicative action
of
and the adjoint action
of
into a joint action
of on
. A minor algebraic miracle occurs here, namely that this combined action is still a genuine action of the Lie algebra
. In particular one has
for all , as can be verified by a brief computation. Also, because the action of
was already faithful on
, this enlarged action of
will still be faithful on
.
Remark 1 One can explain this “miracle” by working first in the larger universal algebra
. This space has a left multiplicative action
of
, but also has a right multiplicative action
which commutes with the left multiplicative action. Furthermore, the splitting
induces a projection map
which will be a Lie algebra homomorphism because
is an ideal. This gives a projected right multiplicative action
which still commutes with the left multiplicative action. In particular, the combined action
is still an action of
. One then observes that this action preserves
, and when restricted to that space, becomes precisely (5).
Now we need to project the above construction down to a finite-dimensional representation. It turns out to be convenient not to use the original representation directly, but only indirectly via the property
. Specifically, we consider the (two-sided) ideal
of
generated by
-fold products of elements in
, and then consider the quotient algebra
. Because
, this algebra still maps to
; since
was faithful in
, it must also be faithful in
.
The point of doing this quotienting is that whereas is likely to be infinite-dimensional, the space
is only finite-dimensional. Indeed, it is generated by those monomials (3) whose total degree
is less than
; since
is finite-dimensional, there are only finitely many such monomials.
From the Leibniz rule (4) we see that the adjoint action of on
preserves
, and thus descends to an action on
. We can combine this action with the multiplicative action of
as before using (5) to create an action of
on
, which is now a finite-dimensional representation which (as observed previously) is faithful on
.
The only remaining thing to show is that for some sufficiently large , that
annihilates
. By linearity, it suffices to show that
whenever
lie in either
or
, and
is a monomial in
. But observe that if one multiplies a monomial
by an element
of
, then one gets a monomial
of one higher degree; and if instead one multiplies a monomial
by an element
of
, then from (4) one gets a sum of monomials in which one of the terms
has been replaced with the “higher order” term
. Using the nilpotency of
(which implies that all sufficiently long iterated commutators must vanish), we thus see that if
is large enough, then
will consist only of terms of degree at least
, which automatically lie in
, and the claim follows.
Remark 2 The above argument gives an effective (though not particularly efficient) bound on the dimension of
and on the order
of
in terms of the dimension of
. Similarly for the arguments we give below to prove more general versions of Ado’s theorem.
— 2. The solvable case —
To go beyond the nilpotent case one needs to use more of the structural theory of Lie algebras. In particular, we will use Engel’s theorem:
Theorem 4 (Engel’s theorem) Let
be a concrete Lie algebra on a finite-dimensional space
which is concretely nilpotent in the sense that every element of
is a nilpotent operator on
. Then there exists a basis of
such that
consists entirely of upper-triangular matrices. In particular, if
is the dimension of
, then
(i.e.
for all
).
The proof of Engel’s theorem is not too difficult, but we omit it here as we have nothing to add to the textbook proofs of this theorem. Note that this theorem, combined with Theorem 3, gives a correspondence between concretely nilpotent Lie algebras and abstractly nilpotent Lie algebras.
Engel’s theorem has the following consequence:
Corollary 5 (Nilpotent ideals are null) Let
be a concrete Lie algebra on a finite-dimensional space
, and let
be a concretely nilpotent Lie algebra ideal of
. Then for any
with at least one of the
in
, one has
.
Proof: Set to be the vector space spanned by vectors of the form
for
and
, then
is a flag, with
mapping
to
for each
. As
is an ideal of
, we see that each of the spaces
is invariant with respect to
. Thus
also maps
to
for each
, and so must have zero trace.
This leads to the following curious algebraic fact:
Corollary 6 Let
be a concrete Lie algebra on a finite-dimensional space
, and let
,
be ideals of
such that
. If
is concretely nilpotent, then
is also concretely nilpotent.
Proof: Let . We need to show that
is nilpotent. By the Cayley-Hamilton theorem, it suffices to show that
for each
. Since
, it suffices to show that
for each
,
, and
. But we can use the cyclic property of trace to rearrange
We can then use the Leibniz rule to expand
But lies in
, and the claim now follows from Corollary 5.
We can apply this corollary to the radical of an (abstract) finite-dimensional Lie algebra
, defined as the maximal solvable ideal of the Lie algebra. (One can easily verify that the vector space sum of two solvable ideals is again a solvable ideal, which implies that the radical is well-defined.)
Theorem 7 Let
be a finite-dimensional (abstract) Lie algebra, and let
be a solvable ideal in
. Then
is an (abstractly) nilpotent ideal of
.
Proof: Without loss of generality we may take to be the radical of
.
Let us first verify the theorem in the case when is a concrete Lie algebra over a finite-dimensional vector space
. We let
be the derived series of
. One easily verifies that each of the
are ideals of
. We will show by downward induction on
that the ideals
are concretely nilpotent. As
is solvable, this claim is trivial for
large enough. Now suppose that
is such that the ideal
is concretely nilpotent. This ideal contains
, which is then also concretely nilpotent. By Corollary 6, this implies that the ideal
is concretely nilpotent, and hence the smaller ideal
is also concretely nilpotent. By a second application of Corollary 6, we conclude that
is also concretely nilpotent, closing the induction. This proves the theorem in the concrete case.
To establish the claim in the abstract case, we simply use the adjoint representation, which effectively quotients out the centre of
(which will also be an ideal of
) to convert an finite-dimensional abstract Lie algebra into a concrete Lie algebra over a finite-dimensional space. We conclude that the quotient of
by the central ideal
is nilpotent, which implies that
is nilpotent as required.
This has the following corollary. Recall that a derivation on an abstract Lie algebra
is a linear map such that
for each
. Examples of derivations include the inner derivations
for some fixed
, but
Corollary 8 Let
be a finite-dimensional (abstract) Lie algebra, and let
be a solvable ideal in
. Then for any derivation
,
is nilpotent.
Proof: If were an inner derivation, the claim would follow easily from Theorem 7. In the non-inner case, the trick is simply to view
as an inner derivation coming from an extension of
. Namely, we work in the enlarged Lie algebra
, which is the Cartesian product
with Lie bracket
One easily verifies that this is an (abstract) Lie algebra which contains as a subalgebra. The derivation
on
then arises from the inner derivation on
coming from
. The claim then easily follows by applying Theorem 7 to this enlarged algebra.
Remark 3 I would be curious to know if there is a more direct proof of Corollary 8 (which in particular did not need the full strength of Engel’s theorem), as this would give a simpler proof of Ado’s theorem in the solvable case (indeed, it seems almost equivalent to that theorem, especially in view of Lie’s theorem).
Define the nilradical of an (abstract) finite-dimensional Lie algebra to be the maximal nilpotent ideal in
. One can verify that the sum of two nilpotent ideals is again a nilpotent ideal, so the nilradical is well-defined. One can verify that the radical
is characteristic (i.e. preserved by all derivations), and so
is also characteristic; in particular, it is an ideal. We conclude that
is in fact contained in the nilradical of
.
We can now prove Ado’s theorem in the solvable case:
Theorem 9 (Ado’s theorem for solvable Lie algebras) Let
be a finite-dimensional solvable Lie algebra. Then there exists a finite-dimensional faithful representation
of
. Furthermore, if
is the nilradical of
, one can ensure that
is nilpotent.
Proof: This is similar to the proof of Theorem 3. We induct on the relative dimension of
relative to its nilradical. When this dimension is zero, the claim follows from Theorem 3, so we assume that this dimension is positive, and the claim has already been proven for lesser dimensions.
Using the adjoint representation as before, it suffices to establish a representation which is nilpotent on and faithful on the centre
. As the centre is contained in the nilradical, it will suffice to establish nilpotency and faithfulness on
.
As in the proof of Theorem 3, we can find a codimension one ideal of
that contains
, and so can split
as vector spaces, for some abelian one-dimensional Lie algebra
. Note that the nilradical of
is characteristic in
, and hence a nilpotent ideal in
; as a consequence, it must be identical to the nilradical
of
.
By induction hypothesis, we have a finite-dimensional faithful representation which is nilpotent on
; we extend this representation to the universal enveloping algebra
. In particular (by Engel’s theorem), there exists a natural number
such that
.
Let be the two-sided ideal in the universal enveloping algebra
generated by the kernel
(in the universal enveloping algebra
, not the Lie algebra) and
. Then the ideal
is contained in the kernel of
. Since
is faithful on
, we see that the quotient map from
to
is also faithful on
.
By the Cayley-Hamilton theorem, for every element of
there is a monic polynomial
of
that is annihilated by
and is thus in
. The monic polynomial
is thus in
. Using this, we see that we can express any monomial (3) with at least one sufficiently large exponent
in terms of monomials of lower degree modulo
. From this we see that
can be generated by just finitely many such monomials, and is in particular finite-dimensional.
The Lie algebra has an adjoint action on
. These are derivations on
, so by Corollary 8, they take values in
and in particular in
. If we extend these derivations to the universal enveloping algebra
by the Leibniz rule (cf. (4)), we thus see that these derivations preserve
, and thus (by the Leibniz rule) also preserve
. Thus this also gives an action of
on
by derivations.
In analogy with (5), we may now combine the actions of and
on
to an action of
which will remain faithful and nilpotent on
, and the claim follows.
— 3. The general case —
Finally, we handle the general case. Actually we can use basically the same argument as in preceding cases, but we need one additional ingredient, namely Levi’s theorem:
Theorem 10 (Levi’s theorem) Let
be a finite-dimensional (abstract) Lie algebra. Then there exists a splitting
as vector spaces, where
is the radical of
and
is another Lie algebra.
We remark that necessarily has trivial radical and is thus semisimple. It is easy to see that the quotient
is semisimple; the entire difficulty of Levi’s theorem is to ensure that one can lift this quotient back up into the original space
. This requires some knowledge of the structural theory of semisimple Lie algebras. The proof will be omitted, as I have nothing to add to the textbook proofs of this result.
Using Levi’s theorem and Theorem 9, one obtains the full Ado theorem:
Theorem 11 (Ado’s theorem for general Lie algebras) Let
be a finite-dimensional Lie algebra. Then there exists a finite-dimensional faithful representation
of
. Furthermore, if
is the nilradical of
, one can ensure that
is nilpotent.
Theorem 11 is deduced from Theorem 9 (and Theorem 10) using almost exactly the same argument used to deduce Theorem 9 from the induction hypothesis, with the key point again being Corollary 8 that places the adjoint action of on
inside
.
Remark 4 One corollary of Ado’s theorem is Lie’s third theorem, which asserts that every finite-dimensional Lie algebra
is isomorphic to the Lie algebra of some Lie group. Indeed, without loss of generality we may take
to be a concrete finite-dimensional Lie algebra in, say,
. We can then consider the (infinite-dimensional) group
of continuously differentiable paths
with
for every
, quotiented out by reparameterisation and by right-translation, with the group law given by concatenation, and then the (finite-dimensional) quotient group
formed by also quotienting out by homotopies that fix the endpoints. One can give
a topology (and a smooth structure) by using neighbourhoods of the origin in
, pushed forward by the exponential map, as a neighbourhood base for
; one can then verify that this is a Lie group with Lie algebra
. We omit the details.

27 comments
Comments feed for this article
10 May, 2011 at 11:16 pm
David Roberts
Hi Terry,
there are some funny TeX errors in the paragraph starting “The only remaining thing to show is that for some sufficiently large…”, including some orphaned ‘langle’s and left-pointing turnstiles.
[Corrected, thanks – T.]
11 May, 2011 at 9:14 pm
Leif
So do you expect most people who read your posts to understand them..or only trained mathematicians who understand the jargon..and I’m assuming that is part of the reason you post links within your posts to Wikipedia articles and other links to help explain concepts or theories you refer to?
Thanks in advance for your response,
Leif
12 May, 2011 at 8:04 am
Terence Tao
12 May, 2011 at 7:37 am
Someone
On mathoverflow (http://mathoverflow.net/questions/8784/why-is-lies-third-theorem-difficult) there was a discussion about the question “Why is Ado’s theorem difficult?”.
16 May, 2011 at 1:23 am
Vanessa Pérez Arroyo
Hy Terry. On the Theorem 3. Let n be a finite dimensional k-step nilpotent Lie algebra, and set m := min { j : ad(x)^j=0 for all x in n } which is a counterexample to m=k?
16 May, 2011 at 9:13 am
Terence Tao
I believe it is possible to build a Lie algebra for which k > m. Some (lengthy) calculations involving the free 4-step nilpotent Lie algebra on four generators suggest to me that one can enforce the constraint that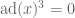 for each x, and still have a non-trivial fourth term in the lower central series.
for each x, and still have a non-trivial fourth term in the lower central series.
17 May, 2011 at 12:17 pm
Ramdorai
Hello Vanessa. Such a Lie algebra as you are considering is called an m-Engel Lie algebra (this notion has been very widely studied by Efim Zelmanov in the case of infinite dimensions). I do not know a counterexample in the case of finite dimension.
In <> ( http://www.springerlink.com/content/j7562232386266w8/ ) your question appear as a conjecture.
11 June, 2011 at 4:15 am
Ravi
I think there is a typo in (the statement of) Corollary 5. It should read “… $\text{tr}(X_1\ldots X_m)=0$” (not “… $\text{tr}(AX_1\ldots X_m)=0$”).
Ravi Raghunathan
[Corrected, thanks – T.]
14 June, 2011 at 7:07 am
Wolfgang M.
Some (historical) remarks which may be of interest to some:
(1.) The above proof, in which a representation of a subspace is inductively extended to the whole Lie algebra, indeed seems to be the ‘standard’ proof for Ado’s theorem. A slightly different approach, by Y. Neretin (“A CONSTRUCTION OF FINITE-DIMENSIONAL FAITHFUL
REPRESENTATION OF LIE ALGEBRA,” http://www.ams.org/mathscinet-getitem?mr=1982443), can be found in the literature.
The objects and techniques used in his proof are almost exactly the same but with the following difference: Neretin first embeds the (complex, finite-dimensional) Lie algebra into a Lie algebra
into a Lie algebra 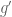 that is the semidirect product
that is the semidirect product 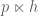 of a reductive Lie algebra
of a reductive Lie algebra  and a nilpotent ideal
and a nilpotent ideal  such that the
such that the  acts completely reducibly on the
acts completely reducibly on the  . It then suffices to find a (finite-dimensional) faithful representation of
. It then suffices to find a (finite-dimensional) faithful representation of 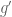 . This is done exactly as in the proof above: by letting
. This is done exactly as in the proof above: by letting 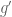 act on its universal enveloping algebra
act on its universal enveloping algebra 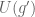 through derivations (p) and left multiplications (h), and then considering the quotient
through derivations (p) and left multiplications (h), and then considering the quotient 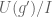 , where
, where 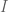 is an invariant ideal that is spanned by all elements that are long enough, in some sense.
is an invariant ideal that is spanned by all elements that are long enough, in some sense.
The embedding theorem follows from what Neretin calls “elementary expansions,” based on the Jordan-Chevalley decomposition for derivations. I suppose this idea is also implicitly contained in the standard proof.
Neretin’s proof is short and elegant, but it also assumes theorem 7, corollary 8, theorem 10, and so on.
(2.) Concerning “Remark 2”: There have been attempts to determine (bounds for) the minimal degree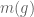 of a faithful representation of a given Lie algebra
of a faithful representation of a given Lie algebra  in terms of other natural invariants associated to
in terms of other natural invariants associated to  . Some classes admit polynomial bounds, but the general bounds appear to be exponential in the dimension.
. Some classes admit polynomial bounds, but the general bounds appear to be exponential in the dimension.
17 August, 2011 at 7:04 pm
Notes on local groups « What’s new
[…] this first for Parts 1 and 2. Let be a Lie algebra. Applying Ado’s theorem (discussed in this blog post), we can identify with a subalgebra of the Lie algebra for some finite . If is a small symmetric […]
1 September, 2011 at 6:15 pm
254A, Notes 1: Lie groups, Lie algebras, and the Baker-Campbell-Hausdorff formula « What’s new
[…] a global Lie group, requiring the non-trivial algebraic tool of Ado’s theorem (discussed in this previous blog post); see Exercise 20 […]
29 October, 2011 at 11:25 am
Associativity of the Baker-Campbell-Hausdorff formula « What’s new
[…] With the assistance of Ado’s theorem, which places inside the general linear Lie algebra for some , one can deduce both the well-definedness and associativity of (3) from the Baker-Campbell-Hausdorff formula for . However, Ado’s theorem is rather difficult to prove (see for instance this previous blog post for a proof), and it is natural to ask whether there is a way to establish these facts without Ado’s theorem. […]
5 April, 2012 at 4:02 am
Theo
Just above Remark 1; why is the enlarged action still faithful on \mathfrak{a}? Couldn’t an element of \mathfrak{h} sit in the centralizer of \mathfrak{a} in \mathfrak{n}?
thanks
5 April, 2012 at 7:18 am
Terence Tao
The restriction of the action of on
on 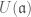 to
to  is simply the original action of
is simply the original action of  on
on 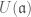 , as can be seen by substituting
, as can be seen by substituting 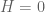 into (5). The behaviour of
into (5). The behaviour of 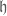 becomes irrelevant at that point.
becomes irrelevant at that point.
21 September, 2012 at 3:28 am
Ado’s theorem for groups with dilations? « chorasimilarity
[…] proof I am aware of, (see this post for one proof and relevant links), mixes the following […]
27 April, 2013 at 9:25 pm
Notes on the classification of complex Lie algebras | What's new
[…] to be a homomorphism into a concrete Lie algebra . It is a deep theorem of Ado (discussed in this previous post) that every abstract Lie algebra is in fact isomorphic to a concrete one (or equivalently, that […]
25 January, 2014 at 10:18 pm
The Lie Bracket | Wet Savanna Animals
[…] Terence Tao, “Ado’s Theorem”; a proof of Ado’s theorem sketched out on Terre… […]
21 March, 2014 at 5:44 am
The Lie Bracket and the Little Adjoint Representation | Wet Savanna Animals
[…] Terence Tao, “Ado’s Theorem”; a proof of Ado’s theorem sketched out on Terre… […]
15 June, 2014 at 6:48 pm
Chapter 13: Lie Theoretical Systems Theory | Wet Savanna Animals
[…] Terence Tao, “Ado’s Theorem”; a proof of Ado’s theorem sketched out on Terre… […]
17 July, 2014 at 9:48 pm
Lie’s Third Theorem and Differential Equations in a Less-Than-Full-Rank Lie Algebra | Wet Savanna Animals
[…] Terence Tao, “Ado’s Theorem”; a proof of Ado’s theorem sketched out on Terre… […]
17 January, 2015 at 2:54 pm
Geoffrey J.
Dear Terry Tao,
I was wondering why one need to take the ideal A to be of codimension 1? Already in the nilpotent case for example, i don’t see in which step we need A to satisfy that (also do we need H to be abelian?). I get the feeling that it is enough to be able to decompose the lie algebra into A \oplus H with A an ideal of the lie algebra.
Thanks for your answer!
Best regards
17 January, 2015 at 5:42 pm
Terence Tao
If is not of codimension 1, it is not obvious how to locate a complementary space
is not of codimension 1, it is not obvious how to locate a complementary space 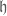 which is itself a Lie algebra (i.e. closed under Lie bracket). In the codimension one case, this is not a difficulty as any one-dimensional subspace is automatically a Lie algebra. (It is automatically also abelian, but this is a bonus which, as you say, is not particularly essential to the rest of the argument.)
which is itself a Lie algebra (i.e. closed under Lie bracket). In the codimension one case, this is not a difficulty as any one-dimensional subspace is automatically a Lie algebra. (It is automatically also abelian, but this is a bonus which, as you say, is not particularly essential to the rest of the argument.)
18 January, 2015 at 1:10 am
Avi Levy
Ctrl + f: “remins” -> “remains”
[Corrected, thanks – T.]
18 March, 2015 at 9:41 am
Alejandro Ginory
Hello Terence Tao,
This as a very enjoyable post. Thanks for posting it.
Regarding remark 3, I don’t know if this qualifies as a more “direct” proof but corollary 8 can be proved via Lie’s theorem and vice-versa. In one direction, corollary 8 can be proved using Lie’s theorem by first showing that any derivation maps the radical of
maps the radical of 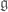 into itself and second by using Lie’s theorem on the solvable ideal
into itself and second by using Lie’s theorem on the solvable ideal 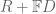 , where
, where  is the image of
is the image of  in
in  under the ad map, to show that
under the ad map, to show that ![[D,rad(\mathfrak{g})]](https://s0.wp.com/latex.php?latex=%5BD%2Crad%28%5Cmathfrak%7Bg%7D%29%5D&bg=ffffff&fg=545454&s=0&c=20201002) is nilpotent.
is nilpotent.
Conversely, corollary 8 can be used to prove Lie’s theorem inductively by taking a solvable Lie algebra , a codimension 1 ideal
, a codimension 1 ideal  , and then showing that the space
, and then showing that the space  generated by 1-dimensional ideals of
generated by 1-dimensional ideals of  is both a non-trivial subspace (by induction) and an ideal in
is both a non-trivial subspace (by induction) and an ideal in  Showing that
Showing that  is an ideal requires cor. 8 and this produces a common eigenvector of the adjoint representation, showing that every solvable ideal has a complete flag consisting of ideals. From there, we can work out Lie’s theorem for any representation
is an ideal requires cor. 8 and this produces a common eigenvector of the adjoint representation, showing that every solvable ideal has a complete flag consisting of ideals. From there, we can work out Lie’s theorem for any representation  by considering the direct sum
by considering the direct sum  , where
, where  is considered as an abelian ideal.
is considered as an abelian ideal.
As a bonus, theorem 7 also follows from cor. 8 and Lie’s theorem.
Best Regards,
Alejandro Ginory
9 May, 2016 at 8:14 pm
Math Major
Dear Prof. Tao,
Thanks for writing this illuminating article. Regarding the statement
“One can of course define Lie algebras over other fields than the complex numbers {{\bf C}}, but in order to avoid some technical issues we shall work solely with the complex case in this post.”
made at the beginning of the post, could you please point out which part of the argument depends on this restriction to complex Lie algebras? I’ve not been able to figure out why the argument won’t go through for real Lie algebras, although Fulton and Harris deduce the real case from the complex case.
Thanks ever so much!
9 May, 2016 at 9:39 pm
Terence Tao
It’s important to restrict to the characteristic zero case (Levi’s theorem fails for positive characteristic, and there may be other places in the above post where characteristic zero is implicitly used). But I think most of the discussion on the complex case transfers to the real case without difficulty (Lie’s theorem isn’t true over the reals, but that theorem isn’t really used in the above post except as motivation). And as you say, the complex case of Ado’s theorem implies the real case as a corollary.
9 September, 2016 at 1:55 pm
Vincenzo Zaccaro
How I can cite your work?
Best regards
Vincenzo
[This particular article was reprinted as Section 2.3 of this book: https://terrytao.wordpress.com/books/hilberts-fifth-problem-and-related-topics/ . In general, the web URL should be fairly stable. -T.]