One of the basic problems in analytic number theory is to estimate sums of the form
as , where
ranges over primes and
is some explicit function of interest (e.g. a linear phase function
for some real number
). This is essentially the same task as obtaining estimates on the sum
where is the von Mangoldt function. If
is bounded,
, then from the prime number theorem one has the trivial bound
but often (when is somehow “oscillatory” in nature) one is seeking the refinement
where is the Möbius function, refinements such as (1) are similar in spirit to estimates of the form
Unfortunately, the connection between (1) and (4) is not particularly tight; roughly speaking, one needs to improve the bounds in (4) (and variants thereof) by about two factors of before one can use identities such as (3) to recover (1). Still, one generally thinks of (1) and (4) as being “morally” equivalent, even if they are not formally equivalent.
When is oscillating in a sufficiently “irrational” way, then one standard way to proceed is the method of Type I and Type II sums, which uses truncated versions of divisor identities such as (3) to expand out either (1) or (4) into linear (Type I) or bilinear sums (Type II) with which one can exploit the oscillation of
. For instance, Vaughan’s identity lets one rewrite the sum in (1) as the sum of the Type I sum
the Type I sum
the Type II sum
and the error term , whenever
are parameters, and
are the sequences
and
Similarly one can express (4) as the Type I sum
the Type II sum
and the error term , whenever
with
, and
is the sequence
After eliminating troublesome sequences such as via Cauchy-Schwarz or the triangle inequality, one is then faced with the task of estimating Type I sums such as
or Type II sums such as
for various . Here, the trivial bound is
, but due to a number of logarithmic inefficiencies in the above method, one has to obtain bounds that are more like
for some constant
(e.g.
) in order to end up with an asymptotic such as (1) or (4).
However, in a recent paper of Bourgain, Sarnak, and Ziegler, it was observed that as long as one is only seeking the Mobius orthogonality (4) rather than the von Mangoldt orthogonality (1), one can avoid losing any logarithmic factors, and rely purely on qualitative equidistribution properties of . A special case of their orthogonality criterion (which actually dates back to an earlier paper of Katai, as was pointed out to me by Nikos Frantzikinakis) is as follows:
Proposition 1 (Orthogonality criterion) Let
be a bounded function such that
for any distinct primes
(where the decay rate of the error term
may depend on
and
). Then
Actually, the Bourgain-Sarnak-Ziegler paper establishes a more quantitative version of this proposition, in which can be replaced by an arbitrary bounded multiplicative function, but we will content ourselves with the above weaker special case. (See also these notes of Harper, which uses the Katai argument to give a slightly weaker quantitative bound in the same spirit.) This criterion can be viewed as a multiplicative variant of the classical van der Corput lemma, which in our notation asserts that
if one has
for each fixed non-zero
.
As a sample application, Proposition 1 easily gives a proof of the asymptotic
for any irrational . (For rational
, this is a little trickier, as it is basically equivalent to the prime number theorem in arithmetic progressions.) The paper of Bourgain, Sarnak, and Ziegler also apply this criterion to nilsequences (obtaining a quick proof of a qualitative version of a result of Ben Green and myself, see these notes of Ziegler for details) and to horocycle flows (for which no Möbius orthogonality result was previously known).
Informally, the connection between (5) and (6) comes from the multiplicative nature of the Möbius function. If (6) failed, then exhibits strong correlation with
; by change of variables, we then expect
to correlate with
and
to correlate with
, for “typical”
at least. On the other hand, since
is multiplicative,
exhibits strong correlation with
. Putting all this together (and pretending correlation is transitive), this would give the claim (in the contrapositive). Of course, correlation is not quite transitive, but it turns out that one can use the Cauchy-Schwarz inequality as a substitute for transitivity of correlation in this case.
I will give a proof of Proposition 1 below the fold (which is not quite based on the argument in the above mentioned paper, but on a variant of that argument communicated to me by Tamar Ziegler, and also independently discovered by Adam Harper). The main idea is to exploit the following observation: if is a “large” but finite set of primes (in the sense that the sum
is large), then for a typical large number
(much larger than the elements of
), the number of primes in
that divide
is pretty close to
:
A more precise formalisation of this heuristic is provided by the Turan-Kubilius inequality, which is proven by a simple application of the second moment method.
In particular, one can sum (7) against and obtain an approximation
that approximates a sum of by a bunch of sparser sums of
. Since
we see (heuristically, at least) that in order to establish (4), it would suffice to establish the sparser estimates
for all (or at least for “most”
).
Now we make the change of variables . As the Möbius function is multiplicative, we usually have
. (There is an exception when
is divisible by
, but this will be a rare event and we will be able to ignore it.) So it should suffice to show that
for most . However, by the hypothesis (5), the sequences
are asymptotically orthogonal as
varies, and this claim will then follow from a Cauchy-Schwarz argument.
— 1. Rigorous proof —
We will need a slowly growing function of
, with
as
, to be chosen later. As the sum of reciprocals of primes diverges, we see that
as . It will also be convenient to eliminate small primes. Note that we may find an even slower growing function
of
, with
as
, such that
Although it is not terribly important, we will take and
to be powers of two. Thus, if we set
to be all the primes between
and
, the quantity
goes to infinity as .
Lemma 2 (Turan-Kubilius inequality) One has
Proof: We have
On the other hand, we have
and thus (if is sufficiently slowly growing)
Similarly, we have
The expression is equal to
when
, and
when
. A brief calculation then shows that
if is sufficiently slowly growing. Inserting these bounds into (8), the claim follows.
From (8) and the Cauchy-Schwarz inequality, one has
which we rearrange as
Since goes to infinity, the
term is
, so it now suffices to show that
Write . Then we have
for all but
values of
(if
is sufficiently slowly growing). The exceptional values contribute at most
which is acceptable. Thus it suffices to show that
Partitioning into dyadic blocks, it suffices to show that
uniformly for , where
are the primes between
and
.
Fix . The left-hand side can be rewritten as
so by the Cauchy-Schwarz inequality it suffices to show that
We can rearrange the left-hand side as
Now if is sufficiently slowly growing as a function of
, we see from (5) that for all distinct
, we have
uniformly in ; meanwhile, for
, we have the crude bound
The claim follows (noting from the prime number theorem that ).
— 2. From Möbius to von Mangoldt? —
It would be great if one could pass from the Möbius asymptotic orthogonality (4) to the von Mangoldt asymptotic orthgonality (1) (or equivalently, to (2)), as this would give some new information about the distribution of primes. Unfortunately, it seems that some additional input is needed to do so. Here is a simple example of a conditional implication that requires an additional input, namely some quantitative control on “Type I” sums:
Proposition 3 Let
be a bounded function such that
for each fixed
(with the decay rate allowed to depend on
). Suppose also that one has the Type I bound
for all
and some absolute constant
, where the implied constant is independent of both
and
. Then one has
and thus (by discarding the prime powers and summing by parts)
Proof: We use the Dirichlet hyperbola method. Using (3), one can write the left-hand side of (11) as
We let be a slowly growing function of
to be chosen later, and split this sum as
If is sufficiently slowly growing, then by (9) one has
uniformly for all
. If
is sufficiently slowly growing, this implies that the first term in (12) is also
. As for the second term, we dyadically decompose it and bound it in absolute value by
By summation by parts, we can bound
and so by (10), we can bound (13) by
This sum evaluates to , and the claim follows since
goes to infinity.
Note that the trivial bound on (10) is , so one needs to gain about two logarithmic factors over the trivial bound in order to use the above proposition. The presence of the supremum is annoying, but it can be removed by a modification of the argument if one improves the bound by an additional logarithm by a variety of methods (e.g. completion of sums), or by smoothing out the constraint
. However, I do not know of a way to remove the need to improve the trivial bound by two logarithmic factors.

14 comments
Comments feed for this article
22 November, 2011 at 2:02 am
Ben Green
Terry,
Interesting post. Proposition 3 interests me, in particular. There would seem to be some hope of using it to understand horocycle flows along the primes, because (9) can probably be obtained from Ratner’s theorem as B-S-Z do, whilst the stronger quantitative estimate (10) requires only an understanding of flows on , and not on the product
, and not on the product 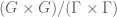 . As I understand it, quite a lot is known in that setting.
. As I understand it, quite a lot is known in that setting.
Ben
22 November, 2011 at 8:51 am
Terence Tao
Yes, this does seem hopeful. Tammy just pointed me towards Theorem
4.54.11 of this paper of Sarnak and Ubis, in particular, which is analogous to our own polynomially quantitative Ratner-type theorem on nilmanifolds, which in principle (when combined with the Vinogradov lemma and Siegel-Walfisz) should indeed give something very close to (10). We’ll ask Peter whether he thinks this might work, as this is probably the quickest way to settle the question. :-)22 November, 2011 at 9:38 am
Ben Green
Terry,
Yes indeed. My feeling is that one is in the game so long as it is not necessary to understand quantitative distribution results on $G/\Gamma \times G/\Gamma$, which is beyond current techniques.
Ben
22 November, 2011 at 9:44 am
Adrián Ubis
Dear Ben and Terence,
it is indeed possible to get (10) from my paper with Peter Sarnak,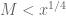 ! I think we could improve it a little, but the problem is that you need (10), as far as I can see, for any
! I think we could improve it a little, but the problem is that you need (10), as far as I can see, for any  ; in particular, for
; in particular, for  larger than
larger than  this seems to me out of reach of any method using just harmonic analysis on the modular surface.
this seems to me out of reach of any method using just harmonic analysis on the modular surface.
but just for
In other words, you need essentially any level for type I sums, which is typically quite hard to get.
Best,
Adrian.
22 November, 2011 at 10:29 am
Terence Tao
Ah, I see the difficulty now: to get effective equidistribution on the discrete horocycle orbits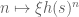 via the methods in your paper one needs a polynomial bound on s, which blocks one from getting the full range of (10). In contrast, when the equidistribution results of Ben and myself for nilflow orbits
via the methods in your paper one needs a polynomial bound on s, which blocks one from getting the full range of (10). In contrast, when the equidistribution results of Ben and myself for nilflow orbits  , there is no bound required on g (and indeed there is a lifting trick of Furstenberg that lifts a nilflow with unbounded g to a higher-dimensional nilflow with bounded g), which is what allows one to get (10) with no bound on M. (And if one only has qualitative equidistribution on the Mobius side, there is no effective bound for M in terms of x.)
, there is no bound required on g (and indeed there is a lifting trick of Furstenberg that lifts a nilflow with unbounded g to a higher-dimensional nilflow with bounded g), which is what allows one to get (10) with no bound on M. (And if one only has qualitative equidistribution on the Mobius side, there is no effective bound for M in terms of x.)
Still, the problem is at least reduced to a statement purely about quantitative equidistribution of horocycle flow, which, while still difficult, at least doesn’t have any primes in it…
22 November, 2011 at 11:06 am
Adrián Ubis
Exactly, that is the trouble. Anyway, as you both point, it is really nice that now one “only” needs to control the horocycle flow in the modular surface, instead of having to know either about products of the modular surface or about the primes themselves.
26 November, 2011 at 7:04 am
Ewan Delanoy
Minor typo : at the very beginning of the post, “for some real number $p$” should be “for some real number $\alpha$”. [Corrected, thanks – T.]
9 June, 2012 at 7:39 am
js
A remark on the derivation of proposition 1 : applying (a corollary of) Selberg’s version of the Bessel inequality (lemma 1.7 in Montgomery’s “Topics in multiplicative number theory”) to vectors $\phi_p : n \mapsto f(pn)$ and $\xi = \mu$ (with notations from the reference above), one immediately gets the result (once Turan-Kubilius is applied).
16 July, 2012 at 9:07 am
pzorin
It took me some time to figure out what js meant, so I will spell out his/her argument here. Lemma 1.7 from the reference says that for vectors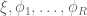 in a Hilbert space one has
in a Hilbert space one has
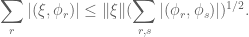
This is used to estimate
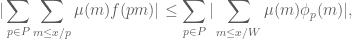
 .
.
where
The lemma provides the estimate
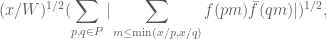

 depends on p and q.
depends on p and q.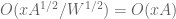 as required.
as required.
and the hypothesis allows to bound this by
where the bound
If H grows sufficiently slowly then the remaining sum is O(x) and this gives the estimate
14 October, 2012 at 5:43 pm
The Chowla conjecture and the Sarnak conjecture « What’s new
[…] control on the error terms than , in particular gains of some power of are usually needed. See this previous blog post for more discussion.) Remark 1 The Chowla conjecture resembles an assertion that, for chosen […]
24 February, 2015 at 11:29 am
254A, Supplement 6: A cheap version of the theorems of Halasz and Matomaki-Radziwill | What's new
[…] a criterion of Katai and Bourgain-Sarnak-Ziegler for Möbius orthogonality estimates in this previous blog post. See also Section 5 of Notes 1 for some similar […]
17 March, 2015 at 10:16 pm
An averaged form of Chowla’s conjecture | What's new
[…] uniformly for all . For “major arc” , close to a rational for small , we can establish this bound from a generalisation of a recent result of Matomaki and Radziwill (discussed in this previous post) on averages of multiplicative functions in short intervals. For “minor arc” , we can proceed instead from an argument of Katai and Bourgain-Sarnak-Ziegler (discussed in this previous post). […]
27 December, 2017 at 9:55 am
Correlations of the von Mangoldt and higher divisor functions II. Divisor correlations in short ranges | What's new
[…] functions, we used Plancherel’s theorem to estimate the global norm , and then also used the Katai-Bourgain-Sarnak-Ziegler orthogonality criterion to control local norms , where was a minor arc interval of length about , and these two estimates […]
20 July, 2018 at 8:06 pm
A viewpoint on Katai’s orthogonality criterion | I Can't Believe It's Not Random!
[…] to do so to keep the main idea more clear, one can find a good presentation of the full proof in Tao’s blog post on the […]