Perhaps the most important structural result about general large dense graphs is the Szemerédi regularity lemma. Here is a standard formulation of that lemma:
Lemma 1 (Szemerédi regularity lemma) Let
be a graph on
vertices, and let
. Then there exists a partition
for some
with the property that for all but at most
of the pairs
, the pair
is
-regular in the sense that
whenever
are such that
and
, and
is the edge density between
and
. Furthermore, the partition is equitable in the sense that
for all
.
There are many proofs of this lemma, which is actually not that difficult to establish; see for instance these previous blog posts for some examples. In this post I would like to record one further proof, based on the spectral decomposition of the adjacency matrix of , which is essentially due to Frieze and Kannan. (Strictly speaking, Frieze and Kannan used a variant of this argument to establish a weaker form of the regularity lemma, but it is not difficult to modify the Frieze-Kannan argument to obtain the usual form of the regularity lemma instead. Some closely related spectral regularity lemmas were also developed by Szegedy.) I found recently (while speaking at the Abel conference in honour of this year’s laureate, Endre Szemerédi) that this particular argument is not as widely known among graph theory experts as I had thought, so I thought I would record it here.
For reasons of exposition, it is convenient to first establish a slightly weaker form of the lemma, in which one drops the hypothesis of equitability (but then has to weight the cells by their magnitude when counting bad pairs):
Lemma 2 (Szemerédi regularity lemma, weakened variant) . Let
be a graph on
vertices, and let
. Then there exists a partition
for some
with the property that for all pairs
outside of an exceptional set
, one has
whenever
, for some real number
, where
is the number of edges between
and
. Furthermore, we have
Let us now prove Lemma 2. We enumerate (after relabeling) as
. The adjacency matrix
of the graph
is then a self-adjoint
matrix, and thus admits an eigenvalue decomposition
for some orthonormal basis of
and some eigenvalues
, which we arrange in decreasing order of magnitude:
We can compute the trace of as
Among other things, this implies that
for all .
Let be a function (depending on
) to be chosen later, with
for all
. Applying (3) and the pigeonhole principle (or the finite convergence principle, see this blog post), we can find
such that
(Indeed, the bound on is basically
iterated
times.) We can now split
where is the “structured” component
and is the “pseudorandom” component
We now design a vertex partition to make approximately constant on most cells. For each
, we partition
into
cells on which
(viewed as a function from
to
) only fluctuates by
, plus an exceptional cell of size
coming from the values where
is excessively large (larger than
). Combining all these partitions together, we can write
for some
, where
has cardinality at most
, and for all
, the eigenfunctions
all fluctuate by at most
. In particular, if
, then (by (4) and (6)) the entries of
fluctuate by at most
on each block
. If we let
be the mean value of these entries on
, we thus have
for any and
, where we view the indicator functions
as column vectors of dimension
.
Next, we observe from (3) and (7) that . If we let
be the coefficients of
, we thus have
and hence by Markov’s inequality we have
for all pairs outside of an exceptional set
with
for any , by (10) and the Cauchy-Schwarz inequality.
Finally, to control we see from (4) and (8) that
has an operator norm of at most
. In particular, we have from the Cauchy-Schwarz inequality that
for any .
Let be the set of all pairs
where either
,
,
, or
One easily verifies that (2) holds. If is not in
, then by summing (9), (11), (12) and using (5), we see that
for all . The left-hand side is just
. As
, we have
and so (since )
If we let be a sufficiently rapidly growing function of
that depends on
, the second error term in (13) can be absorbed in the first, and (1) follows. This concludes the proof of Lemma 2.
To prove Lemma 1, one argues similarly (after modifying as necessary), except that the initial partition
of
constructed above needs to be subdivided further into equitable components (of size
), plus some remainder sets which can be aggregated into an exceptional component of size
(and which can then be redistributed amongst the other components to arrive at a truly equitable partition). We omit the details.
Remark 1 It is easy to verify that
needs to be growing exponentially in
in order for the above argument to work, which leads to tower-exponential bounds in the number of cells
in the partition. It was shown by Gowers that a tower-exponential bound is actually necessary here. By varying
, one basically obtains the strong regularity lemma first established by Alon, Fischer, Krivelevich, and Szegedy; in the opposite direction, setting
essentially gives the weak regularity lemma of Frieze and Kannan.
Remark 2 If we specialise to a Cayley graph, in which
is a finite abelian group and
for some (symmetric) subset
of
, then the eigenvectors are characters, and one essentially recovers the arithmetic regularity lemma of Green, in which the vertex partition classes
are given by Bohr sets (and one can then place additional regularity properties on these Bohr sets with some additional arguments). The components
of
, representing high, medium, and low eigenvalues of
, then become a decomposition associated to high, medium, and low Fourier coefficients of
.
Remark 3 The use of spectral theory here is parallel to the use of Fourier analysis to establish results such as Roth’s theorem on arithmetic progressions of length three. In analogy with this, one could view hypergraph regularity as being a sort of “higher order spectral theory”, although this spectral perspective is not as convenient as it is in the graph case.

15 comments
Comments feed for this article
3 December, 2012 at 7:52 pm
Shubhendu Trivedi
I have general question about Remark 3 (but concerning Szemeredi Regular Partitions). I apologize if it is too elementary.
A simple algorithm to generate a regular partition by Frieze-Kannan is over here http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.44.721 (they mention the paper that you cite over here as well). Note that here they only consider the first singular value to check for regularity at each stage.
My question is: Why wouldn’t this work for a Hypergraph Case? I understand that there is no analog for “SVD” for tensors. That is, the best rank approximation for
rank approximation for  order tensor
order tensor  ,
, 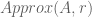 has no solutions in general. The notable exceptions are two specific cases (for rank one tensors i.e.
has no solutions in general. The notable exceptions are two specific cases (for rank one tensors i.e. 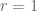 and when
and when 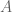 is a matrix i.e.
is a matrix i.e.  . Since in the Graph case the first singular value is all that we need, shouldn’t this work for the hypergraph case as well?
. Since in the Graph case the first singular value is all that we need, shouldn’t this work for the hypergraph case as well?
4 December, 2012 at 2:57 pm
Terence Tao
There is a subtlety in the hypergraph case which has to do with the fact that there are several different types of hypergraph regularity one could ask for. In particular there is an “order 1” hypergraph regularity which does indeed fit well with rank one approximation, but in many applications one actually needs a higher order notion of hypergraph regularity which does not interact well with bounded rank approximations.
To explain this, begin with the graph case. An edge set E can be viewed as an indicator function of two vertex-valued variables
of two vertex-valued variables 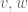 . Graph regularity has to do with understanding sums such as
. Graph regularity has to do with understanding sums such as
and this can be done by using the SVD to split into finite rank components such as
into finite rank components such as  .
.
Now consider a 3-uniform hypergraph, which now comes with an indicator function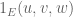 . If one were interested in counting “order 1” sums such as
. If one were interested in counting “order 1” sums such as
then a bounded rank approximation to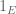 would be effective; this would correspond, roughly speaking, to the hypergraph regularity lemma of Chung. But in practice, this type of regularity is insufficient; one often needs to count expressions such as
would be effective; this would correspond, roughly speaking, to the hypergraph regularity lemma of Chung. But in practice, this type of regularity is insufficient; one often needs to count expressions such as
for some graphs F,G,H, and bounded rank approximations can be quite terrible for this purpose. (See for instance the discussion in this paper of Gowers.) In particular, there are 3-uniform hypergraphs with no bounded rank approxmiations which have nontrivial behaviour with respect to sums such as (*). Instead one has to consider “order 2” bounded rank approximations to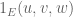 , using linear combinations of functions of the form
, using linear combinations of functions of the form  rather than
rather than  . (These two-variable functions
. (These two-variable functions  in turn then need to be approximated by “order 1” bounded rank functions.) This can still be done, but one is now quite far from the classical theory of rank.
in turn then need to be approximated by “order 1” bounded rank functions.) This can still be done, but one is now quite far from the classical theory of rank.
5 December, 2012 at 2:05 pm
Shubhendu Trivedi
Couldn’t thank you enough for your answer!
So if I understood correct, there should still be a way to obtain Chung’s version in a simple algorithmic way as in the graph case suggested by Frieze and Kannan.
More precisely, there should be an analog of Lemma 2 in http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.44.721 for the higher order case.
That is, something along these lines must hold:
/// Let be a
be a  dimensional Tensor
dimensional Tensor  , with
, with  and
and  . If
. If 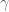 is a small positive real number then,
is a small positive real number then,
(a) if there exists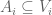 such that
such that  and
and 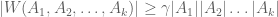 then
then 
(b) if then there exists
then there exists  such that
such that  and
and 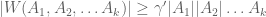 where
where  ,
,  is a constant. Such
is a constant. Such  might be constructed in polynomial time. ///
might be constructed in polynomial time. ///
Is this a correct way of thinking about it?
5 December, 2012 at 2:47 pm
Terence Tao
Well, I don’t know how exactly you will be defining the greatest singular value of a tensor, but something along these lines should be possible. Note that one can also essentially prove Chung’s regularity lemma by viewing a hypergraph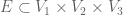 (say) first as a graph between
(say) first as a graph between  and
and  , applying the usual regularity lemma to this, and then applying the regularity lemma one further time to the components of
, applying the usual regularity lemma to this, and then applying the regularity lemma one further time to the components of  obtained from the first application of that lemma. (Actually, to make all this work properly, it is more convenient to work with a strong version of the regularity lemma that has an additional function parameter F.
obtained from the first application of that lemma. (Actually, to make all this work properly, it is more convenient to work with a strong version of the regularity lemma that has an additional function parameter F.
5 December, 2012 at 2:50 pm
Shubhendu Trivedi
Thanks a lot again for your reply!
PS: Minor comment. One tag is misspelled as “eigenvales”.
[Corrected, thanks -T.]
3 December, 2012 at 8:19 pm
David Roberts
A couple of orphaned/mismatched html tags:
In the paragraph after Lemma 1:
[Fixed, thanks – T.]
4 December, 2012 at 12:57 am
Craig
Hi Terry,
I am not a mathematician or anything. Just a college undergrad studying their gen eds…
But reading a quote from Paul Graham, from the link on the left of your blog, which was an amazing read by the way,
“To a newly arrived undergraduate, all university departments look much the same. The professors all seem forbiddingly intellectual and publish papers unintelligible to outsiders. But while in some fields the papers are unintelligible because they’re full of hard ideas, in others they’re deliberately written in an obscure way to seem as if they’re saying something important. This may seem a scandalous proposition, but it has been experimentally verified, in the famous Social Text affair. Suspecting that the papers published by literary theorists were often just intellectual-sounding nonsense, a physicist deliberately wrote a paper full of intellectual-sounding nonsense, and submitted it to a literary theory journal, which published it.”
I hope you are not writing anything in an obscure way to seem as if what you are writing is important :(
Sincerely,
Craig
16 December, 2012 at 2:25 pm
davetweed
Note that the quote’s logic isn’t quite right. Submitting a paper full of nonsense (which has been done in other disciplines, eg, theoretical physics) isn’t capable of experimentally verifying that a substantial number of the papers in a discipline are nonsense, only that papers in the discipline can’t be reliably distinguished from nonsense. (The proposition may well still be true, but that’s not established by this test.)
Even with my cynics hat on, I’m more inclined towards the weaker interpretation: referees have no strong incentive to actually understand a paper rather than just see if anything it says looks “obviously wrong”.
10 December, 2012 at 5:47 pm
Anonymous
In (1), Lemma 2, should $d_{i,j} |V_i| |V_j|$ be $d_{i,j} |A| |B|$ ?
[Corrected, thanks – T.]
28 December, 2012 at 6:07 am
Balazs Szegedy
Dear Terry,
For the sake of clompleteness let me mention that I wrote a paper about the spectral proof of the stronng regularity lemma which clarifies the same issues that you discuss (see below). It may also contain some new interesting aspect. (For example connection to graph limits and group theory)
Limits of kernel operators and the spectral regularity lemma
http://arxiv.org/abs/1003.5588
European J. of Comb, Volume 32, Issue 7, October 2011, p. 1156-1167
[Thanks, I’e added a link to this in the main post. Good to see that we now have spectral proofs of the weak, strong, and standard regularity lemmas in the literature – T.]
15 January, 2013 at 3:15 pm
Anonymous
Don’t want to sound uncaring for your precious time at all. If at all it comes across like that, I apologize for it. But I was wondering if it would ever be possible to have an expository post for the paper Balazs just posted?
I have spent a couple of months trying to understand it but it seems impregnable but at the same time very important and deep.
Regards.
29 October, 2013 at 8:09 pm
A spectral theory proof of the algebraic regularity lemma | What's new
[…] group. It turns out that the spectral proof of the Szemerédi regularity lemma (discussed in this previous blog post) adapts very nicely to this setting. The key fact needed about definable sets over finite fields is […]
29 March, 2014 at 5:31 am
Anonymous
two lines below inequality (10): should be
should be  ?
?
[Corrected, thanks – T.]
24 April, 2014 at 3:11 pm
A proof of Roth’s theorem | What's new
[…] and “highly pseudorandom” components, as is common in the subject (e.g. in this previous blog post), but even though we crucially need to retain non-negativity of one of the components in this […]
13 November, 2015 at 1:16 pm
The spectral proof of the Szemeredi regularity lemma | Systems, Networks and Control
[…] Source: The spectral proof of the Szemeredi regularity lemma […]