The classical foundations of probability theory (discussed for instance in this previous blog post) is founded on the notion of a probability space – a space
(the sample space) equipped with a
-algebra
(the event space), together with a countably additive probability measure
that assigns a real number in the interval
to each event.
One can generalise the concept of a probability space to a finitely additive probability space, in which the event space is now only a Boolean algebra rather than a
-algebra, and the measure
is now only finitely additive instead of countably additive, thus
when
are disjoint events. By giving up countable additivity, one loses a fair amount of measure and integration theory, and in particular the notion of the expectation of a random variable becomes problematic (unless the random variable takes only finitely many values). Nevertheless, one can still perform a fair amount of probability theory in this weaker setting.
In this post I would like to describe a further weakening of probability theory, which I will call qualitative probability theory, in which one does not assign a precise numerical probability value to each event, but instead merely records whether this probability is zero, one, or something in between. Thus
is now a function from
to the set
, where
is a new symbol that replaces all the elements of the open interval
. In this setting, one can no longer compute quantitative expressions, such as the mean or variance of a random variable; but one can still talk about whether an event holds almost surely, with positive probability, or with zero probability, and there are still usable notions of independence. (I will refer to classical probability theory as quantitative probability theory, to distinguish it from its qualitative counterpart.)
The main reason I want to introduce this weak notion of probability theory is that it becomes suited to talk about random variables living inside algebraic varieties, even if these varieties are defined over fields other than or
. In algebraic geometry one often talks about a “generic” element of a variety
defined over a field
, which does not lie in any specified variety of lower dimension defined over
. Once
has positive dimension, such generic elements do not exist as classical, deterministic
-points
in
, since of course any such point lies in the
-dimensional subvariety
of
. There are of course several established ways to deal with this problem. One way (which one might call the “Weil” approach to generic points) is to extend the field
to a sufficiently transcendental extension
, in order to locate a sufficient number of generic points in
. Another approach (which one might dub the “Zariski” approach to generic points) is to work scheme-theoretically, and interpret a generic point in
as being associated to the zero ideal in the function ring of
. However I want to discuss a third perspective, in which one interprets a generic point not as a deterministic object, but rather as a random variable
taking values in
, but which lies in any given lower-dimensional subvariety of
with probability zero. This interpretation is intuitive, but difficult to implement in classical probability theory (except perhaps when considering varieties over
or
) due to the lack of a natural probability measure to place on algebraic varieties; however it works just fine in qualitative probability theory. In particular, the algebraic geometry notion of being “generically true” can now be interpreted probabilistically as an assertion that something is “almost surely true”.
It turns out that just as qualitative random variables may be used to interpret the concept of a generic point, they can also be used to interpret the concept of a type in model theory; the type of a random variable is the set of all predicates
that are almost surely obeyed by
. In contrast, model theorists often adopt a Weil-type approach to types, in which one works with deterministic representatives of a type, which often do not occur in the original structure of interest, but only in a sufficiently saturated extension of that structure (this is the analogue of working in a sufficiently transcendental extension of the base field). However, it seems that (in some cases at least) one can equivalently view types in terms of (qualitative) random variables on the original structure, avoiding the need to extend that structure. (Instead, one reserves the right to extend the sample space of one’s probability theory whenever necessary, as part of the “probabilistic way of thinking” discussed in this previous blog post.) We illustrate this below the fold with two related theorems that I will interpret through the probabilistic lens: the “group chunk theorem” of Weil (and later developed by Hrushovski), and the “group configuration theorem” of Zilber (and again later developed by Hrushovski). For sake of concreteness we will only consider these theorems in the theory of algebraically closed fields, although the results are quite general and can be applied to many other theories studied in model theory.
— 1. Qualitative probability theory – generalities —
We begin by setting up the foundations of qualitative probability theory, proceeding by close analogy with the more familiar quantitative probability theory (though of course we will have to jettison various quantitative concepts, such as mean and variance, from the theory).
As discussed in the introduction, we are replacing the unit interval by the three-element set
; one could view this as the quotient space of
in which the interior
has been contracted to a single point
. This space is still totally ordered:
. The addition relation
on
contracts to an “addition” relation
on
, defined by the following rules:
with no other relations of the form in
. Strictly speaking,
is not a binary operation here, as
can evaluate to
or to
, but we keep the notation
in order to emphasise the analogy with quantitative probability theory.
A qualitative probability space is then a space
equipped with a Boolean algebra
(the measurable subsets of
) and a function
with
, which is finitely additive in the sense that
whenever
are disjoint. It is easy to see that these measures are monotone (thus
whenever
), and that
. A measurable subset
of
is called a
-null set if
, and a
-full set, a
-conull set, or a
-generic set if
; note that
-full sets are the complements of
-null sets and vice versa. A property
of points
is said to hold
-almost everywhere or for
-generic
if it holds outside of a
-null set (or equivalently, if it holds on a
-generic set).
One can describe a qualitative probability measure on a Boolean space
purely through its null ideal
of null sets, or equivalently through its full filter
of full sets. Conversely, if a subset
of
is the full filter of some qualitative probability measure on
if it obeys the following filter axioms:
- (Empty set)
and
.
- (Monotonicity) If
are in
, and
, then
.
- (Intersection) If
, then
.
Furthermore is completely determined by the filter
. Similarly for the null ideal (with suitably inverted axioms, of course). Thus, if one wished, one could replace the concept of a qualitative probability measure with the concept of an ideal or filter, but we retain the use of
to emphasise the probabilistic interpretation of these objects.
One obvious way to create a qualitative probability measure is to start with a quantitative probability measure and “forget” the quantitative aspect of this measure by quotienting down to
. Under some reasonable hypotheses, one can reverse this procedure and view many qualitative probability measures as quantitative probability measures to which this forgetful process has been applied. However, this reversal is usually not unique, and we will not try to use it here.
In quantitative probability theory, one can take two quantitative probability measures on the same space
and form an average
for some
, which is another quantitative probability measure. For instance, if
is a probability measure and
is a set with measure between
and
, then
can be expressed as an average of the conditioned measures
and
.
In analogy with this, we can take two qualitative measures on the same space
and form the average
, defined by setting
if and only if
(or equivalently,
if and only if
). If
is a qualitative probability measure and
is a set with measure
, then we can form the conditioned measure
, defined by setting
if
(or equivalently
if
), and then one can check that
is the average of the conditioned measures
and
.
We call a qualitative probability measure irreducible if it does not assign any set the intermediate measure of (or equivalently, the full filter is an ultrafilter); thus, irreducible qualitative probability measures are the same concept as finitely additive
-valued probability measures (which, as is well known, are essentially the same concept as ultrafilters). By the previous discussion, we see that a qualitative probability measure is irreducible if and only if it is not the average of two other measures.
In this paper we will primarily work with irreducible measures, but will occasionally have to deal with reducible measures, for instance when taking the conditional product (or pullback) of two irreducible measures over a third.
Given a measurable map between two Boolean spaces
,
(thus the pre-image of any measurable set in
by
is measurable in
), we can define the pushforward
of any qualitative probability measure
on
to be the qualitative probability measure on
defined by the usual formula
. In particular, if
embeds into
, then any measure
on
can also be viewed as a measure on
, which we call the extension of
to
.
We now discuss the issue of product measures in the qualitative setting. Here we will deviate a little from the usual probability formalism, in which one usually defines a product algebra to be the minimal algebra that contains the Cartesian product of
and
. Here, it turns out to be more useful to have a more flexible (but not unique) notion of a product, in which more measurable sets are permitted. Namely, given two Boolean spaces
,
, we say that a Boolean space
is a product of the two spaces if
is the Cartesian product of
and
, and the following axioms are obeyed:
- (Products) If
and
, then
.
- (Slicing) If
, then
for all
, and
for all
.
These axioms do not uniquely specify , but in practice each product space
will have a canonical choice for
attached to it.
Given two qualitative probability spaces ,
, a qualitative probability space
is a product of the two spaces if
is a product of
and
, and the following assertions are equivalent for any
:
-
.
- For
-almost every
,
.
- For
-almost every
,
.
Of course, one could replace by
here in the above equivalence, which can be thought of as a qualitative Fubini-Tonelli type theorem. Once one selects the product Boolean algebra
, the product measure
is uniquely specified, if it exists at all; but (as in the setting of classical measure theory if one is not working with
-finite measures), existence is not always automatic. (But in our applications, it will be.)
One can define products of more than two (but still finitely many) qualitative probability spaces in a similar fashion; we leave the details to the reader.
Now we are ready to set up qualitative probability theory. We need a qualitative probability space to serve as the sample space, event space, and probability measure. An event in
is said to occur almost surely if it occurs on a
-full set. Given an Boolean space
, a random variable is then a measurable map
. We permit random variables that are only defined almost surely, thus
is now a partial function defined on a
-full event in
; as in quantitative probability theory or measure theory, we view random variables that agree almost surely as being essentially equivalent to each other. The law or distribution of
is the pushforward
of the qualitative probability measure; this is then a qualitative measure on
. We say that two random variables
agree in distribution, and write
, if they have the same law.
Two random variables ,
are said to be independent if the distribution of the joint random variable
is the product of the distributions of
and
separately. Here we need to specify a product Boolean algebra
on the product space
to make this definition well-defined, but in the applications we will consider, we will always have a canonical product algebra to select. One can define independence of more than two random variables in a similar fashion.
At the opposite extreme to independence, we say that a random variable is determined by another random variable
if there is a measurable map
such that
almost surely. The constrast between independence and determination (as well as a weaker property than determination we will consider later, namely algebraicity) will be the focus of the group chunk and group configuration theorems discussed in later sections.
As discussed in this previous blog post, in quantitative probability theory we often reserve the right to extend the underlying probability space , in order to introduce new sources of randomness, without destroying the probabilistic properties of existing random variables (such as their independence and determination properties). We say that an extension of a qualitative probability space
is another qualitative probability space
together with a measurable map
such that
. One can then pull back any random variable
to a random variable
on the new probability space; by abuse of notation, we continue to refer to
as
. Probabilistic notions such as independence, law, or determination remain unchanged under such an extension.
— 2. Qualitative probability theory on definable sets —
For the purposes of this post, the qualitative probability measures we will care about will live in the theory of algebraically closed fields. We will assume some basic familiarity with algebraic geometry concepts, such as the dimension of a variety. The exact choice of field will not be important here, but one could work with the complex field
if desired (in which case one could (somewhat artificially) model the qualitative probability measures here by quantitative probability measures on complex varieties if one wished).
Henceforth is fixed; in contrast to usual model theory practice, we will not need to introduce some sufficiently large extension of
to work in. The notion of measurability here will be given by the model-theoretic concept of definability. Namely, a definable set is a set
of the form
for some predicate that can be expressed in terms of the field operations
, a finite number of variables and constants in
, the boolean symbols
, the equality sign, the quantifiers
(with all variables being quantified over
), and punctuation symbols (parentheses and colons). A definable map
between two definable sets is a function whose graph
is a definable set.
As is algebraically closed, the definable sets can be described quite simply. Define an irreducible quasiprojective variety, or variety for short, to be a Zariski-open dense subset of an irreducible affine variety over
. One can show (using elimination of quantifiers in algebraically closed fields, the existence of which follows from Hilbert’s nullstellensatz) that a set is definable if and only if it is the union of a finite number of disjoint varieties.
We equip each definable set with the Boolean algebra
of definable subsets of
; this will be the only algebra we shall ever place on a definable set. Note that if
are definable, then
is a product space of
and
as per the previous definition.
If is a qualitative probability measure on a definable set
, the support of
is defined to be the intersection of all the Zariski-closed sets of
-full measure. As the Zariski topology is Noetherian, the support is always a closed set of full measure.
Remark 1 One can describe a qualitative probability measure
through its type, defined as the set of all predicates
which hold for
-almost all
. This concept is essentially the same as the concept of a type in model theory; the measure
is irreducible if and only if the type is complete. In this post, we have essentially replaced the notion of a type with that of a qualitative probability measure, and so types will not appear explicitly in the rest of the post.
We now give some basic examples of qualitative probability measures on definable sets.
Example 1 If
is a non-empty definable set of some dimension
(that is,
is the largest dimension of all components of
(or of its closure)), then the qualitative uniform probability measure
on
(or uniform measure, for short) is defined by setting all subsets of dimension
or less to have measure zero, or equivalently all generic subsets of
(that is,
with finitely many sets of dimension
removed) to have full measure. (Sets which contain a generic subset of some, but not all, of the
-dimensional components of
, then are assigned the intermediate measure.) The support of this measure is then the closure of the union of the
-dimensional components. This measure is irreducible if and only if
is almost irreducible in the sense that it only has one
-dimensional component. Note that the algebraic geometry notion of genericity now coincides with the (qualitative) probabilistic notion of almost sureness: a (definable) property on
holds generically if and only if it holds almost surely with respect to the uniform measure on
.
If
are definable sets, then the uniform measure on
is the product of the uniform measure on
and the uniform measure on
; the proof of the Fubini-Tonelli type statement that justifies this may be found for instance in Lemma 13 of this paper of mine.
Example 2 If
is almost irreducible and
is a definable map, then the uniform measure
on
pushes forward to the uniform measure of some almost irreducible subset
of
; see e.g. Lemma A.8 of this previous paper of Breuillard, Green, and myself. Also, generic points in
have fibres in
of dimension
, just as one would expect from naive dimension counting. If
is not almost irreducible, the situation becomes a bit more complicated because the image on
on different components of
may have a different dimension, and so
may become an average of uniform measures on sets of different dimension.
Exercise 1 Let
be a qualitative probability measure on a definable set
.
- (i) Show that
is irreducible if and only if it is the uniform measure of some almost irreducible subset of
.
- (ii) Show that
is the average of finitely many uniform measures if and only if there does not exist a countable family of disjoint subsets of
of positive measure. (Hint: greedily select disjoint varieties of
of positive measure, starting with zero-dimensional varieties (points) and then increasing the dimension.)
We now use the formalism of qualitative probability theory from the previous section, but always working within the definable category; thus we require the sample space to also be a definable set, and that all random variables are required to be definable maps (or at least generically definable maps), which is a stronger condition than measurability.
— 3. The group chunk theorem —
Random variables can interact very nicely with groups , if they come equipped with an appropriate invariant measure. To illustrate this, let us first return to the classical setting of quantitative probability theory, working exclusively with finite groups to avoid all measurability issues.
Given a finite group , let
be two elements of
chosen uniformly and independently at random, and then form their product
. This gives us a triple
of random variables taking values in
, which obey the following independence and determination properties:
- (i) (Uniform distribution) For any
,
has the uniform distribution on
.
- (ii) (Independence) For any distinct
,
are independent.
- (iii) (Determination) For any distinct
,
is determined by
.
- (iv) (Associativity) After extending the sample space as necessary, one can locate additional random variables
taking values in
such that
(see figure), and such that any other triple
for distinct
which is not a permutation of the four triples already mentioned is jointly independent.
Indeed, to see the associativity axiom, let be selected uniformly from
independently of
, and set
and
. The associativity is depicted graphically in the figure below, in which three points connected by a line or curve indicate a dependence, but triples of points not joined by such a line or curve being independent.
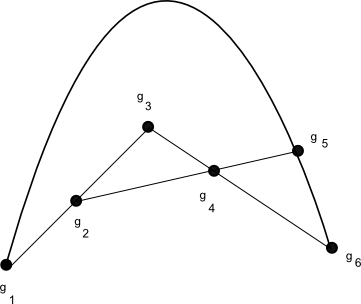
In the converse direction, any triple on a finite set
obeying the above axioms necessarily comes from an underlying group operation:
Proposition 1 (Probabilistic description of a finite group) Let
be a finite non-empty set, and let
be random variables on
that obey axioms (i)-(iv). Then there exists a group structure
on
such that
.
Proof: By axiom (iii), we have for some binary operation
. From axiom (iv) we have
almost surely (and hence surely, as is finite); also from axioms (i), (iv) we see that
is uniformly distributed in
. We conclude that the binary operation
is associative, thus
for all
.
By axiom (iii), we see that for fixed ,
is determined by
and vice versa; from axioms (i), (ii), this implies that for fixed
, the map
is a bijection from
to itself; similarly the map
is a bijection from
to itself. Note also from associativity that
commutes with the right-action of
in the sense that
for all
.
Conversely, given any bijection that commutes with the right-action in the sense that
for all
, we claim that
for a unique
. Indeed, from axioms (i)-(iii), we know that
is determined by
, and so for any given
, we may find
such that
. If this holds for a single
, then it holds for all other
by associativity, since
commutes with the right action, and the map
is a bijection. Thus we may identify
with the space of bijections
that commute with the right-action. This is clearly a group, and the property
is then clear from construction.
Now that we see that a finite group, at least, may be described in terms of the probabilistic language of independence and determination. It is natural to ask whether similar results hold for infinite groups (with the slight modification that we now only expect to hold almost surely rather than surely, as we now will have non-trivial events of probability zero). Here we run into the technical difficulty that many groups – such as non-compact Lie groups, or algebraic groups defined over fields other than
or
– are not naturally equipped with a probability measure with which to define the concept of uniform distribution. However, if one is working in the definable category, one can use the language of qualitative probability theory instead and obtain the same result.
A definable group is a group
which is a definable set, such that the group operations
and
are definable maps. This notion is very close to, but subtly different from, that of the more commonly used notion of an algebraic group; the latter is a bit stricter because the group has to now be an algebraic variety, and the group operations have to be regular maps and not just definable maps. However, the two notions are quite close to each other, particularly in characteristic zero when they become equivalent up to definable group isomorphism, although additional subtleties arise in positive characteristic
due to the existence of things like the inverse Frobenius automorphism
, which is definable but not regular, and which can be used to definably “twist” an algebraic group. We will not discuss these issues further here, but see this survey of Bouscaren and this article of van den Dries for further discussion.
Theorem 2 (Group chunk theorem) Let
be an almost irreducible definable set, and let
be qualitative random variables taking values in
, obeying axioms (i)-(iv). Then, after passing from
to a generic subset, one may definably identify
with a generic subset of an definable group
, so that
almost surely. (To put it another way, there is a definable bijection
between a generic subset of
and a generic subset of
, such that
almost surely.)
This theorem is essentially due to Weil (although he worked instead in the category of algebraic varieties and algebraic groups, rather than definable sets and definable groups). It was extended to many other model-theoretic contexts (and in particular to stable theories) in the thesis of Hrushovski, although we will only focus on the classical algebraic geometry case here.
A typical example of a group chunk comes from taking a definable group and removing a lower dimensional subset of it, so that the group law is only generically defined (but this is still sufficient for defining almost surely). For instance, one could let
be the
non-singular matrices
, with (generically defined) group law given by matrix multiplication followed by projective normalisation to force the lower left coordinate to be
(which is only defined if this coordinate does not vanish, of course). This can be viewed as an open dense subset of the projective special linear group
, and the theorem is asserting that
can be “completed” to this group, which can be interpreted as a definable group. (
can be viewed as an affine variety using, for instance, the adjoint representation. In any event, even projective varieties can be interpreted affinely in a definable fashion by the artificial device of breaking up the variety into finitely many pieces, which can be all fit into a sufficiently large affine space.)
We now prove Theorem 2. By axioms (i)-(iii), there is a generically defined, and definable, map such that
almost surely. From axiom (iii) we then conclude the following cancellation axioms:
- (vii) (Left cancellation) For generic
, there is a unique
such that
.
- (viii) (Right cancellation) For generic
, there is a unique
such that
.
The associativity axiom then also gives for generic
.
These axioms also imply the following variants:
- (vii’) (Left cancellation) For generic
,
is the unique
such that
.
- (viii’) (Right cancellation) For generic
,
is the unique
such that
.
Indeed, from axiom (vii), we have a generically defined map that maps a generic pair
to
, where
is the unique
such that
. This map is generically injective; as
is essentally irreducible, this map has to be generically bijective also, which gives (vii’), and (viii’) is proven similarly. (We call a partially defined map
generically bijective if it can be made into a total bijection by refining
to generic subsets.) We conclude that for generic
, the maps
and
are generically bijective.
To obtain a genuine group from rather than just a generic group, we perform a formal quotient construction, analogous to how the integers are formally constructed from the natural numbers (or the rationals from the integers). Define a formal pre-group element to be a definable subset
of
with the following properties:
- (ix) (Vertical line test) For generic
, there is exactly one
such that
.
- (ix’) (Vertical line test) For generic
,
is the unique
such that
.
- (x) (Horizontal line test) For generic
, there is exactly one
such that
.
- (x’) (Horizontal line test) For generic
,
is the unique
such that
.
- (xi) (Translation invariance) For generic
,
lies in
.
The axioms (ix)-(x’) are asserting that is a generic bijection. (Here and in the sequel we adopt the convention that a mathematical statement is automatically considered false if one or more of its terms are undefined; for instance,
is only true when
and
is well-defined. Similarly, when using set-builder notation, we only include those elements in the set which are well-defined; for instance, in the set
,
is implicitly restricted to those values for which
and
are well-defined.)
Call two formal pre-group elements are equivalent if they have a common generic subset, and then define a formal group element to be an equivalence class
of formal pre-group elements
, and let
be the space of formal group elements. At this point, we have to deal with the technical problem that
is not obviously a definable set. However, observe that if
is a formal pre-group element, then we have a definable generic bijection
from
to
, which makes
essentially irreducible. If we then define
to be the Zariski closure of the top dimensional component of
(i.e. the support of the uniform measure on
), then
is an irreducible closed variety, which depends only on the equivalence class
of
, with inequivalent pre-group elements giving distinct irreducible closed varieties. Finally, one can describe
in terms of a generic element
of
, as being the closure of the top-dimensional component of
, and generic elements
produce such an objecft. As such, if we let
be the set of all
, then
is in one-to-one correspondence with the space of formal group elements, and may be parameterised as a definable set using standard algebraic geometry tools (e.g. Chow coordinates, the Hilbert scheme, or elimination of imaginaries), as being the image under a generically definable map
of
with fibres of dimension
. In particular, as
is essentially irreducible with dimension
,
is essentially irreducible with dimension
.
We define the identity element of to be the equivalence class of the diagonal
, and define the inverse of the equivalence class of a formal pre-group element
to be the equivalence class of the reflection
of
. As for the group law, we use generic composition: given two formal pre-group elements
, we define the composition
to be the set of all pairs
such that there exists
for which
is the unique element with
, and
is also the unique element with
. One can check (somewhat tediously) that this descends to a well-defined operation on
that gives it the structure of a definable group.
Next, for generic , the set
is a formal pre-group element, giving a generically defined map
. One can verify that this map is generically definable, generically injective, and generically a homomorphism. The remaining task is to verify that
has the same dimension as
, as this together with essential irreducibility and generic injectivity gives generic bijectivity thanks to dimension counting. But for every formal pre-group element
, we see that generic
, there is a unique
with
, and furthermore that
for generic
; in particular,
is equivalent to
and can thus be recovered from
; conversely, generic
gives rise to a formal group element by this construction. This sets up a generically bijective map
from
to
, which shows that
has the same dimension as
, as required. This concludes the proof of Theorem 2.
— 4. The group configuration theorem —
We now discuss a variant of the group chunk theorem that characterises group actions, known as the group configuration theorem. Again, to motivate matters we start with the quantitative probabilistic setting in the finite case. If is a finite group acting on a finite set
, and
are chosen independently and uniformly at random from
, and
uniformly from
(independently of
), and then one defines
,
,and
(or, more symmetrically, we have the constraints
,
,
, and
), then we observe the following independence and determination axioms (setting
and
for
):
- (i’) (Uniform distribution) For any
,
has the uniform distribution on
, and
has the uniform distribution on
.
- (ii’) (Independence) Any two of the random variables
are independent.
- (iii’) (Determination) For any distinct
,
is determined by
, and
is determined by
and
.
- (v) (More independence) Any three of the random variables
that are not of the form
or
for distinct
are independent.
Axiom (ii’) is in fact a consequence of axiom (v), but we add it for emphasis. We refer to a sextet obeying the above axioms as a group configuration. It can be described graphically by the picture below, in which the collinearity of three random variables indicates a dependence between them, with non-collinear triples of variables being independent.

The group configuration theorem concerns a generalisation of the above situation, in which the determination properties in axiom (iii’) are relaxed to the weaker properties of algebraicity. (In additive combinatorics, this would correspond to moving from a “99%” situation in which algebraic structure is present almost everywhere, to a “1%” settng in which it is only present a positive fraction of the time.) We say that one random variable taking values in one definable set
is algebraic with respect to another random variable
taking values in another definable set
if there is a relation
such that
almost surely, and such that for each
there are only finitely many
such that
. More informally,
is algebraic over
if
determines
up to a finite ambiguity. For instance, if
is uniformly distributed in
, then
is algebraic with respect to any non-constant polynomial
of
.
Two random variables are said to be interalgebraic if they are each algebraic over each other. For instance, if
is uniformly distributed in the affine line
, and
are two non-constant polynomials, then
and
are interalgebraic. Note that interalgebraicity is an equivalence relation.
Now we can give the group configuration theorem:
Theorem 3 (Group configuration theorem) Let
be almost irreducible definable sets, and let
be random variables in
respectively on a qualitative probability space obeying the following axioms:
- (i’) (Uniform distribution) For any
,
has the uniform distribution on
, and
has the uniform distribution on
.
- (ii’) (Independence) Any two of the random variables
are independent.
- (iii”) (Interalgebraicity) For any distinct
,
is algebraic over
, and
is algebraic over
and
.
- (v) (More independence) Any three of the random variables
that are not of the form
or
for distinct
are independent.
- (vi) (Irreducibility) The joint random variable
has an irreducible distribution.
Then, after extending the (qualitative) probability space if necessary, there exist a definable group
that acts definably on a definable space
, as well as qualitative random variables
and
uniformly distributed in
and
respectively for
, with
algebraic over
and
interalgebraic with
with
, such that
almost surely, and with the
obeying the same independence and irreducibility hypotheses as the
.
This theorem was first established by Zilber, who worked in the more general setting of strongly minimal theories, and then strengthened significantly in the thesis of Hrushovski, who treated the case of stable theories. (However, in these more general situations, the space is restricted to be “one-dimensional” for technical reasons.) We give a proof below the fold, following an exposition of Hrushovski’s method by Bouscaren. (See also a proof of a result very close to the above theorem, avoiding model-theoretic language, by Elekes and Szabo.) The irreducibility axiom (vi) can be relaxed, but then the conclusion becomes more complicated (there might not be a single group structure or group action involved, but rather an average of such actions).
The group configuration theorem has a number of applications to combinatorics; roughly speaking, this theorem is to “approximately associative” definable maps as Freiman’s theorem is for sets of small doubling. The aforementioned paper of Elekes and Szabo is one example of the configuration theorem in action; another is Theorem 41 of this paper of mine, which I proved by a different method (based on Riemann surface arguments), but for which a stronger statement has since been proven using the group configuration theorem by Hrushovski (private communication).
Now we prove Theorem 3. There are two main phases of the argument. The first phase involves upgrading several of the algebraicity hypotheses in axiom (iii”) to determination, by replacing several of the using algebraic changes of variable. Once this is done, the second phase consists of applying a modification of the proof of the group chunk theorem to locate the definable group
(and also the definable space
that
acts on), and to connect this action to the group configuration.
We begin with a simple dimension counting observation. By the axioms, the random variable has an irreducible distribution and is thus uniformly distributed on some almost irreducible definable set
, with
algebraic over
, which is uniformly distributed on
. Taking dimensions, we conclude that
. Similarly for permutations. This implies that
for some natural number ; a similar argument using the
triples shows that
for some natural number . Next, since
are uniformly distributed on
, and the other three variables
are algebraic over these variables, we see that the tuple
is uniformly distributed on some almost irreducible definable set of dimension
.
We now begin the first phase. Currently, by axiom (iii”), is algebraic over
. We now use further dimension counting upgrade this algebraicity relationship to determination, basically by removing some information from
.
Proposition 4 Let the assumptions be as in Theorem 3. Then there exists a random variable
which is interalgebraic with
and uniformly distributed in some almost irreducible set
, such that
is determined by
.
Proof: Let be the support of
, and let
be the projection of
onto
, then
is a closed variety, and as
is algebraic over
,
is generically finite over
. In particular,
also has dimension
. We then form the pullback (or base change)
of two copies of
over (a generic subset of)
; we view
as a subset of
. This is a definable set, but is not necessarily almost irreducible.
Now consider the projection of
to
. The set
contains the diagonal
and thus has dimension at least
. We claim that
in fact has dimension exactly
. Indeed, suppose this were not the case, then
would contain an irreducible variety
of dimension
for some positive
. Now observe that as
is algebraic over
, the projection of
to
is generically finite over
, which has dimension
; taking pullback with itself, we conclude that the projection of
to
also has dimension
. Thus, over a generic point in
, the fibre of
projected to
has dimension at most
. Similarly, the projection of this fibre to
has dimension at most
. Since
is algebraic over
, we conclude that the generic fibre of
over a point in
has total dimensino at most
, so that the preimage of
in
has dimension at most
and is thus a lower-dimensional component of (or of
after projecting to either of the two copies of
). Thus, if we pass to a suitable generic subset of
, the projection
of
to
has dimension
. Passing to a further generic subset if necessary, we may assume that
is algebraic in the sense that any horizontal or vertical line in
meets
in at most finitely many points. From the Noetherian property, we see that there is in fact a uniform upper bound
on how many such points can lie on a line (this is basically the degree of
).
We now define the random variable to be the set of all
with
, such that
lies in the projection of (the generic portion of
we are working with) to
. By the above discussion, this is a finite subset of
, and the set of all such possible
can be parameterised in a definable way (indeed, it lies inside the
-fold powers of
over
for
), and is interalgebraic with
. By construction,
is also determined by
; as the latter is uniformly distributed on some almost irreducible set,
is also, and the claim follows.
A similar argument provides a random variable interalgebraic with
such that
is determined by
. By replacing
with
respectively, and checking that none of the axioms (i’). (ii’), (iii”), (v), (vi) are destroyed by this replacement, we see that we may reduce without loss of generality to the case in which we have the additional axiom
- (iii”‘)
is determined by
, and
is determined by
.
Now we turn to the task of making determined both by
and by
. We are unable to effectively utilise (suitable permutations of) Proposition 4 here, because any replacement of
by a random variable with less information content will likely destroy axiom (iii”‘). However, we can at least construct a random variable
interalgebraic with
that is determined by the joint random variable
. Indeed, the support
of
is generically finite over
, and by repeating the dimension counting arguments from Proposition 4, we see tht the projection
of the pullback
to
has dimension at most
, and so has finite fibres after passing to a generic subset. If we then set
to be the fibre of
over
, we conclude as before that
is interalgebraic with
, and is clearly determined by
. Also, each element of
, together with
, generically determines
by axiom (iii”‘), and hence
is determined by
; similarly
is determined by
. Thus by replacing
with
, we may impose the additional axiom
- (vii)
is determined by
while retaining all previous axioms.
Now we perform the following “doubling” trick, creating some new random variables by extending the probability space. As before, let be the support of
. As
is uniformly distributed in
, we see that for generic
and generic
, there is a non-zero finite number of tuples
such that
. Similarly there are a non-zero finite number of tuples
such that
. Thus, for generic
, if we let
be the set of all tuples
such that
(see figure), then is a generically finite cover of
(projecting onto the
coordinates). Thus, if we perform a base change of the probability space
(which we view as lying over
) to
, we may now create random variables
with the being an extension of the previous random variables of the same name.
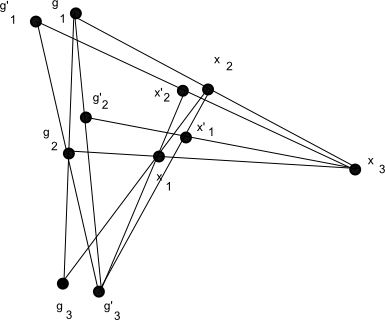
Since is algebraic over
, we see (as
is generic and deterministic) that
is algebraic over
. Similarly
is algebraic over
, and also
is algebraic over
and
is algebraic over
. From (iii) we also see that
is determined by
and
, and
is determined by
and
. Finally from (vii) we see that
determine
, and similarly
determine
. Thus if we set
then we see that
-
is interalgebraic with
for
;
-
is interalgebraic with
for
;
-
is determined by
;
-
is determined by
;
-
is determined by
;
-
is determined by
.
Thus, by replacing and
with
and
, we may now obtain the additional axiom
- (vii’)
is determined by
, and also
is determined by
.
We now have enough determination relations to begin the second phase of the argument, in which the arguments used to prove the group chunk theorem may be applied. Observe that determine
, and
determine
. Thus, for generic
, we have a generically bijective definable map
such that
almost surely, with also depending definably on
. Similarly, for generic
, we have a generically bijective definable map
such that
almost surely, with also depending definably on
.
We now relate the and
to each other:
Lemma 5 After extending the probability space if necessary, there exist random variables
uniformly distributed in
respectively, such that we almost surely have the identity
holds generically. Furthermore, any three of the
are independent, with the fourth being algebraic over these three.
Proof: Let be the generic subset of
consisting of those
such that
(recall from our conventions that these statements implicitly require that all expressions be well-defined, thus for instance must lie in the domain of
for the second statement to be true). The set
surjects onto a subset of
of dimension
(because
is algebraic over
, which is uniformly distributed over
), so the generic fibres have dimension
. If we let
, then
thus has dimension
. We view
as a subset of
and parameterise it as
By a base change, we may then find a set of random variables
uniformly distributed in , which restricts to the existing tuple
of random variables.
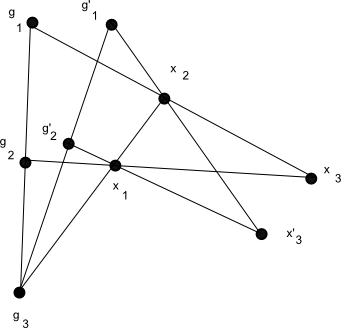
By construction, one has
almost surely. On the other hand, the support of has dimension at most
(because
are algebraic over
) and so for generic choices of these random variables, the set of possible
has dimension at least
; since any one of these variables is algebraic over any other (once the
are fixed), we conclude that
cannot be restricted to any lower-dimensional set than
. We conclude that almost surely, (2) holds generically.
The above discussion shows that the support of has dimension exactly
; as any three of
are such that the remaining two random variables in
are algebraic over these three, the final claims of the lemma follow.
We rewrite (2) as
almost surely, where is the equivalence class of a generically bijective, and definable, partial function
up to generic equivalence, and inversion and composition on such equivalence classes is defined in the obvious manner. This equivalence class can be made definable by identifying
with the closure of the top-dimensional component of the graph
of
, and then expressing this in Chow coordinates (or using the Hilbert scheme); this makes equivalence classes
into random variables uniformly distributed in some definable sets , which are definable images of
and thus almost irreducible (after passing to generic subsets of
if necessary). We thus see that any three of
are independent, and we have the relation
almost surely.
In particular, for fixed choices of ,
,
determines
and vice versa. Thus
and
have the same dimension, say
. (This could be strictly less than
, basically because the original sets
may contain superfluous degrees of freedom which do not interact with the spaces
.)
We now let be the set of all equivalence classes
of generically bijective and definable partial functions
with the following properties:
- For generic
, there exists
such that
.
- For generic
, there exists
such that
.
- For generic
, there exists
such that
.
- For generic
, there exists
such that
.
This is a definable set; is contained in the image of
by the map
with fibres of dimension at most
, and thus can have at most one component of dimension
(and no larger dimensional components); on the other hand, from (5)
contains the image of a generic subset of
; thus
has dimension exactly
and is essentially irreducible.
By construction, contains the (equivalence class of) the identity map on
and is closed under inversion. We also claim that it is closed under composition, which would make
a definable group. Indeed, let
. For generic
, there exists
such that
. The map
is a generic bijection and
is almost irreducible, and so
is generic also. Thus, we may generically also find
such that
, and hence
. This gives the first property required for
to lie in
, and the other three are proven similarly.
Having located the definable group , the next step is to locate a space
that
acts definably on. We first observe that
generically acts on
, by defining
whenever
,
, and
is the unique element of
such that
(which, recall, is the closure of the top-dimensional component of the graph of
) contains
. This is a definable, and generically defined operation which obeys the action axiom
for generic
.
To create a genuine action and not just a generic action, we perform yet another “quotient space construction” to extract a suitable space from
as follows. Define a formal pre-point to be a definable subset
of
obeying the following axioms:
- (xv) (Vertical line test) For generic
, there is exactly one
such that
.
- (xv’) (Vertical line test) For generic
,
is the unique
such that
.
- (xvi) (Translation invariance) For generic
, we have
.
Two formal pre-points are equivalent if they have a common definable subset, and a formal point is an equivalence class of formal pre-points. We then let be the set of all formal points. If
is a formal pre-point and
is a generic element of
, then
is equivalent to
, and so is essentially irreducible; by similar arguments to before, we may now parameterise
as a definable set, which is the image of the generically defined map
described above with fibres of dimension at least
and so has at most one component of dimension
and no higher-dimensional components. The group
acts on formal pre-points by the formula
one easily verifies that this is an action on formal pre-points which descends to a definable action on the space of formal points.
For generic , the set
can be verified to be a formal pre-point; this gives a definable, generically defined map
, which one can check to be generically injective; combined with the previous dimension control on
, we now see that
has dimension
and is almost irreducible, with
generically bijective. It can also be shown to generically preserve the action, in the sense that
for generic
.
Finally, we can set up the random variables and
required for Theorem 3. We choose generic elements
, and then set
It is clear that for generic , the
are interalgebraic with
, and that the relations (1) hold almost surely. Also,
is clearly algebraic over
for
, and the
are uniformly distributed in
. For
, we use the relation
. As
is algebraic over
and
,
is algebraic over
and
. Thus for generic
, there can only be finitely many possible values of
, giving the desired algebraicity.
We see that is uniformly distributed in
; as
almost surely, we conclude that
is uniformly distributed over
. The independence requirements on the
now follow from the corresponding independence hypotheses on the
.

6 comments
Comments feed for this article
16 November, 2013 at 11:05 pm
omar aboura
In the definition of “qualitative probability space” (third paragraph of Section 1), I think that the three must be
must be 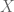 .
.
[Corrected, thanks – T.]
17 November, 2013 at 12:13 am
Allen Knutson
PSL_2(k) isn’t projective; it’s the image of the adjoint representation of SL_2(k). More specifically it’s affine, being SO(the Killing form).
[Corrected, thanks – T.]
17 November, 2013 at 9:58 am
Rex
I believe “projective” here is just referring to the name of PSL and not asserting any projectivity.
[Allen was referring to an earlier version of the text, now corrected, in which there was some confusion in this regard – T.]
3 January, 2014 at 8:46 am
Sean Eberhard
An oft-used countably additive qualitative probability measure, completely unrelated to any genuine measure, is Baire category in a complete metric space. Say that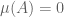 if
if  is meagre and
is meagre and  if
if  is comeagre.
is comeagre.
9 May, 2021 at 10:18 am
Goursat and Furstenberg-Weiss type lemmas | What's new
[…] The ability to encode an abelian additive relation in terms of group-theoretic properties is vaguely reminiscent of the group configuration theorem. […]
13 May, 2021 at 4:48 pm
Goursat and Furstenberg-Weiss type lemmas – scroo0ooge
[…] The ability to encode an abelian additive relation in terms of group-theoretic properties is vaguely reminiscent of the group configuration theorem. […]