Last updated: May 10, 2024
An epsilon of room: pages from year three of a mathematical blog
Terence TaoVolume 1 (Real analysis): Graduate Studies in Mathematics 117, American Mathematical Society, 2010
ISBN-10: 0-8218-5278-7
ISBN-13: 978-0-8218-5278-1
Volume 2: American Mathematical Society, 2011ISBN-10: 0-8218-5280-9
ISBN-13: 978-0-8218-5280-4
This continues my series of books derived from my blog. The preceding books in this series were “Structure and Randomness” and “Poincaré’s legacies“.
Online versions of both volumes can be found here and here respectively.
Vol I. was reviewed for the Bulletin of the London Mathematical Society by Jonathan Partington here.
Errata for Vol. I:
- In some early printed versions, the section numbering of references in the preface are either incorrect or missing. (This only affects a very small number of copies.)
- Page 6: In Exercise 1.1.2, “unique” should be “maximal”. (It should also be stated that in this text, manifolds are assumed to be second countable.. In Exercise 1.1.5, delete the “of” in “and of the algebra of null sets”.
- Page 7: In Example 1.1.14,
should be
.
- Page 8: In the first paragraph of the proof of Theorem 1.1.17, “see that if” should just be “see that”.
- Page 9: In Exercise 1.1.8, add “and let the extension
be the measure constructed in the proof of that theorem” to the end of the first sentence. The portion of the exercise regarding how the assumption of finite measure on
may be dropped in the sigma-finite case is incorrect and should be deleted. In Exercise 1.1.10,
should be
(two occurrences).
- Page 15: In (1.5),
should be
.
- Page 17: Before (1.9), “
should be
“.
- Page 20: In the statement of Theorem 1.2.4, replace
by “
is measurable”. Then add “If
is finite, then
and
is finite”. Also replace “
are finite”with “
” are finite”. In Corollary 1.2.5,
needs to be finite rather than
-finite, and in Corollary 1.2.5 (iii), replace “
” with “
“. After Corollary 1.2.5, add “When
is
-finite rather than finite, the three claims (i), (ii), (iii) in Corollary 1.2.5 are no longer equivalent; however, a modification of the above arguments shows that claim (ii) holds if and only if
for some measurable
with at least one of
absolutely integrable. We take this to be the definition of absolute continuity in the
-finite case.”. Just before Section 1.2.2, add “(One can also complexify this space to obtain a complex vector space of complex finite measures, but we will not use such measures here.)”. In the proof of Corollary 1.2.5, the reference to Theorem 1.2.2 should instead be to Theorem 1.2.4.
- Page 22: After Remark 1.2.8, “”singular continuous”” should be “”absolutely continuous””.
- Page 33: In (1.18),
should be
.
- Page 34: In Exercise 1.3.2 (iv), in the
case the additional hypothesis that
are non-negative is required.
- Page 36: After Exercise 1.3.6, the first sentence should be replaced by “It is easy to see (using the triangle inequality if
, and Exercise 1.3.2 otherwise) that the quasi-norm balls
form a base for a topology on
.” After Remark 1.3.6: Exercise 1.3.5 should be Exercise 1.3.7.
- Page 39: In Exercise 1.3.10,
and
should be
and
respectively.
- Page 41: In the proof of Theorem 1.3.16, “E” should be in math mode (second paragraph) and “g” should be in math mode (end of third paragraph). Just before (1.28),
should be
, and add “(in the sense that the real and imaginary parts are absolutely continuous) after “
is absolutely continuous”.
- Page 42: In the second to last line,
should be
.
- Page 43: At the end of the first sentence:
should be
.
- Page 46: In equation (1.38), the dot product should be an inner product.
- Page 50: In Exercise 1.4.6, “this inequality” should be “this equality”, and “non-empty finite measure” should be “non-zero finite measure”.
- Page 51: In Exercise 1.4.8, a right parenthesis is missing after “of
and
“.
- Page 53: In Remark 1.4.15, “next set of notes” should be “next section”.
- Page 54: In the second and third bullets of Exercise 1.4.16,
should be
.
- Page 55: In Exercise 1.4.18(iv), “take adjoints of (ii)” should be “take adjoints of (iii)”. In Remark 1.1.14, “Remark 1.26” should be “Remark 1.3.19”.
- Page 61: When the notion of isomorphism of normed vector spaces is defined shortly before Exercise 1.5.1, it should be remarked that this is a looser notion than the isometric notion of isomorphism for Hilbert spaces employed after Exercise 1.4.1. (Different categories of isomorphism.) Also, in the definition of equivalence, “continuous linear transformation” should be “bicontinuous linear transformation”.
- Page 62: In Exercise 1.5.7,
should be
.
- Page 63: In Exercise 1.5.10, “
” should be “
“. In Remark 1.5.5, one of the “H”s is incorrectly not set in math mode. In Exercise 1.5.1, the finite-dimensional vector space should also be understood to be normed.
- Page 64: In the second display in the proof of Proposition 1.5.7,
should be
.
- Page 65: In the proof of the complex case of the Hahn-Banach theorem,
should take values in
rather than
.
- Page 65: In Exercise 1.5.14,
should be
. Two lines after 1.5.7, “we see that
has norm at most 1″ should be “we see that
has norm at most 1″. After Exercise 1.5.14, the double dual should be described as the space of continuous linear functions on
.
- Page 66: In Exercise 1.5.15(i), the colon after the first appearance of
should be deleted. One can also add that
denotes the closure of
in
.
- Page 67: In the proof of Theorem 1.5.13,
should be
. In Exercise 1.5.17, “disjoint sets of positive measure” should be “disjoint sets of positive finite measure”.
- Page 68: In Remark 1.5.15, add “, with
is now required to be non-zero”. In Exercise 1.5.18, X should be a real vector space rather than a complex one, and “usual Hahn-Banach theorem” should be “usual Hahn-Banach theorem for real normed vector spaces”.
- Page 72: In Definition 1.6.6, after introducing the notion of an isolated point, add “(a point which is open)”.
- Page 74: In the proof of (ii) implying (i) in Theorem 1.6.8, a closed parenthesis should be added after “converging to
“.
- Page 79: In Example 1.6.21,
should be
.
- Page 80: In Example 1.6.22, “sufficiently large
” should be “sufficiently large
“. In Example 1.6.25, “the direct sum
” should be “the pairing
defined by
“.
- Page 81: In Definition 1.6.29, “partially ordered set” should be “pre-ordered set”. To conform to usual notational conventions, the partial order should be denoted
rather than
.
- Page 87: In the last sentence of the proof of the Baire category theorem,
should be
.
- Page 89: In the third part of Exercise 1.7.4, some reasonable notion of “operator norm” for a nonlinear operator in order to make the question well-posed. One choice that works is the Lipschitz norm, but the reader is invited to experiment with other choices as well. In the proof of Theorem 1.7.5, “must be dense in a ball” should be “one of the
must be dense in a ball”.
- Page 90: In Corollary 1.7.7, Y should be assumed to be Banach space and not merely a normed vector space. In (1.64),
should be
. In the proof of the Corollary, Theorem 1.7.3 should be Theorem 1.7.5. Remark 1.7.8 is incorrect and should be deleted.
- Page 92: In the proof of Theorem 1.7.12,
should be
, and similarly
should be
, and
should be
,
should be
, and
should be
.
- Page 93: In Exercise 1.7.6, the Hahn-Banach theorem is actually not necessary for this exercise. The conclusion “
is an isomorphism” should instead read “
is a linear homeomorphism”.
- Page 94: In Exercise 1.7.7, “we can ensure that” may be clarified to “the above statement remains true if we impose the additional condition that”.
- Page 95: In Example 1.7.18, both occurrences of
should be
. In Remark 1.7.17, “are uncomplemented” should be “is uncomplemented”, and “the appendix” should be “Section 1.7.4”.
- Page 97: In the first paragraph of Section 1.7.4, add the remark that thanks to Exercise 1.7.9, this provides examples of closed subspaces of Banach spaces that are not complemented. The reference to (1.103) can be replaced with Section 1.12.2.
- Page 98: In the proof of Theorem 1.7.22, all occurrences of
should be replaced by
.
- Page 100: “Phi, Isett” should be “Phil Isett”.
- Page 103: Before Exercise 1.8.4, in the definition of an ultrafilter,
should be
.
- Page 104: In Exercise 1.8.8, “basis” should be “base”.
- Page 105: In Exercise 1.8.11, “every sufficiently large
” should be “every sufficiently large
“.
- Page 111: In Exercise 1.8.21, the optional fifth part is incorrect and should be deleted.
- Page 112: In the last bullet point of Definition 1.8.18,
should be
.
- Page 113: In Example 1.8.21, “
” should be “
and
“. In Example 1.8.22, equicontinuity can be upgraded to uniform equicontinuity.
- Page 114:
should be
.
- Page 115: In the first line,
should be
.
- Page 118: In Definition 1.9.1, “is continuous” should be “are continuous”.
- Page 119: At the end of Exercise 1.9.3, add the sentence “Such spaces are known as locally convex topological vector spaces.”. In Example 1.9.4, “topological vector space” should instead read “topological space, but not a topological vector space (because multiplication is not continuous)”, and the final sentence of the example should be deleted.
- Page 120: In Exercise 1.9.7, one needs to require the additional hypothesis that
is finite. Also, the parenthesis after the epsilon in the definition of
needs to be moved to the left of the
sign.
- Page 123: In the second and third parts of Exercise 1.9.13, V (and hence
and
) need to be assumed to be normed vector spaces.
- Page 124: In Remark 1.9.15,
should be
.
- Page 125: In Exercise 1.9.19, the third item is incorrect and should be deleted. “As
” should be “As
“.
- Page 127: In Remark 1.9.17, “proper chain” should be “proper well-ordered chain” throughout.
- Page 129: In Exercise 1.9.25, the first sentence can be deleted (also the word “throughout” should be appended to the last sentence).
- Page 135:
should be
. “the empty set has sup 0” should be “the empty set has sup 1”. In Exercise 1.10.3, “the rationals” should be “the set
consisting of the rationals
“. To put it another way,
is the coarsest topology such that every set that is open in
, is open in
, and such that
is also open.
- Page 134: “Gelfand-Neimark” should be “Gelfand-Naimark”.
- Page 136: In Exercise 1.10.4, “on this finite set” should be “on this countable set”. In Definition 1.10.2,
should be
.
- Page 137: In Proposition 1.10.4, the hypothesis that X is sigma-compact may be deleted, by removing all references to the compact set K in the proof (and also deleting the last sentence of the proof). In Exercise 1.10.7, add the following parenthetical remark: “(This question is easier to prove if one assumes that every non-empty open set has positive measure, but it is also possible to solve the question without this additional hypothesis, by working in the “support” of the measure, that is to say a closed set in which every non-empty open set has finite measure, and then using the Tietze extension theorem.)”. This exercise should thus also be moved to after the Tietze extension theorem.
- Page 139: In Remark 1.10.7, the final
should be an
.
- Page 140: In Exercise 1.10.10, “Then there exists” should be “Show that there exists”. In the proof of Theorem 1.10.8, Theorem 1.10.5 should be Exercise 1.10.10.
- Page 141: In the second part of Exercise 1.10.11, “normal” should be “normal and Hausdorff”. Add the following exercise: “Let
be a locally compact Hausdorff space, and let
be an open cover of
. Show that there exist compactly supported continuous functions
supported on
for each
with
for all
(with only finitely many of the terms on the left-hand side non-zero for each
).”
- Page 146: After “the class of measurable sets is a Boolean algebra”, add “and that
is finitely additive on this Boolean algebra”. The sentence fragment “Each
in this supremum is supported in some closed subset
of
” should be replaced by “For each
, each
in this supremum is bounded by
plus a continuous function between
and
for some closed subset
of
“.
- Page 148: In Lemma 1.10.15, “functions” should read “functionals”, and “
” should read “
“. Exercise 1.10.15 should read as follows: “Show that among all possible choices for the functionals
appearing in the above lemma, there is a unique choice which is minimal in the sense that for any other functionals
obeying the conclusions of the lemma,
and
for all non-negative
.”
- Page 149: After the definition of vague convergence, a remark should be added that an application of the uniform boundedness principle (and Exercise 1.10.7) shows that vague convergence of
to
is equivalent to the
being uniformly bounded in
and that
for all
, however the uniform boundedness aspect cannot be dropped (consider for instance the sequence
on the real line).
- Page 152: In Exercise 1.10.25,
should be
. In Exercise 1.10.24, “Then” should be “Show that”.
- Page 154: In Exercise 1.10.30, the phrase “on compact subsets of
” is redundant and can be deleted. (In the online version of the text, the claim “converges uniformly” should be corrected to “converges pointwise a.e.”.)
- Page 155: In Exercise 1.10.35, insert “when
is self-adjoint” after the second display.
- Page 160: in the last paragraph, the closing parenthesis after (1.80) should instead be after “convex function of
“.
- Page 161: In (1.82),
should be
. In Remark 1.11.4,
should be
. Also, strictly speaking, one should dispose of the degenerate case when
or
, though this case is easy since non-trivial holomorphic functions cannot vanish on a line.
- Page 162: In Exercise 1.11.4,
and
should be
and
respectively, and similarly for
.
- Page 164: After (1.83),
should be
(two occurrences). In the following display,
on the left-hand side should be
. In the fourth proof, “analytic function of
” should be “analytic function of
“. In Exercise 1.11.5, add “up to almost everywhere equivalence”. In the display before (1.84),
should be
.
- Page 166: In the fourth display, the final
should be
. In Example 1.11.6, the first
should be
independent of
. homogeneity rather than quasihomogeneity by working with the non-dyadic Lorentz norm
instead of the dyadic Lorentz norm, which is equivalent up to constants with the dyadic Lorentz norm, although this was not the intent of the exercise.)
- Page 167: In Exercise 1.11.8,
should be
. In the last , the condition
needs to be imposed.
- Page 168: In Exercise 1.11.10,
should take values in
rather than
, and
should be replaced by
.
- Page 169: In the first sentence of Section 1.11.3, “these notes” should be “this section”. In Exercise 1.11.13, add that
is the dual exponent defined by
, and is allowed to be negative in this exercise. Also, it is understood that an assertion such as
is false if
is not absolutely integrable.
- Page 170: In Remark 1.11.8, the second semicolon should be a comma.
- Page 171: “it is in fact convex in all of
” should read “it is also convex in the triangular region
“. In Exercise 1.1.16, “
(resp.
)” should be “
(resp.
)”, and there is an extra whitespace after “a.e.”.
- Page 172: In the definition of a sublinear operator, the additional condition
should be added in addition to
(with a similar modification to Remark 1.11.11). “
is a family of linear operators” should be “
is a family of sub-linear operators”, and
should map to
-valued or
-valued” functions rather than just
-valued functions. In Exercise 1.11.17, the requirement that p be finite or X has finite measure should be imposed through the entire exercise, not just for the uniqueness aspect. As such, when defining strong and weak type, one should only use the second bullet point rather than the first or third bullet point (unless one has finiteness of p or of the measure of X).
- Page 173: Just before Theorem 1.11.10, Marcinkeiwicz should be Marcinkiewicz. The sentence “We say that a linear operator
is of strong type …” is redundant and may be deleted.
- Page 174-175: All occurrences of “(1.91), (1.94)” should be “(1.93), (1.94)”.
- Page 176: In the first display,
should be
. In Remark 1.11.12, there should not be a C in the subscript of
(two occurrences). In Exercise 1.11.18 and Exercise 1.11.19, one also needs to add the hypothesis
.
- Page 177: In Exercise 1.11.21,
should be
.
- Page ???: In Exercise 1.11.22, add the hypothesis
.
- Page 180: In Exercise 1.11.24,
should be
.
- Page 181: In Exercise 1.11.26,the hypothesis
should be
.
- Chapter 12: In general, the discussion in this chapter should be restricted to sigma-compact LCA groups (due to the reliance on Fubini’s theorem and the Riesz representation theorem, both of which become quite delicate outside of this setting.)
- Page 187: In Exercise 1.12.3,
should be
. Exercise 1.12.5 is not correct as stated in the non sigma-compact case. It can be replaced with the following: “Let
be an LCA group with non-trivial Haar measure
. Let
be the space of equivalence classes of functions
such that for every set
of finite measure, the restriction of
to
lies in
with a norm bounded uniformly in
, with two functions in
in the same equivalence class if they agree almost everywhere on every set
of finite measure, and with the
norm of
equal to the supremum of the
norms of the restrictions. (For $\sigma$-finite groups
,
is identical to
, but the two spaces differ slightly in general.) Show that
is identifiable with $\tilde L^\infty(G)$.”.
- Page 188: In Exercise 1.12.7(b), the question is technically solvable as stated, but the “Conversely” portion of the question has a trivial answer as currently written. It should read “For every
,
, and neighbourhood
of the identity, there exists
supported on
such that
” (i.e. the requirement that
has small support is missing). [Actually, this part of the exercise is rather tricky and is not strictly needed for the rest of the exercise; I will probably split it off into a separate exercise in the next edition of this text.]
- Page 189: In Exercise 1.12.7(g), “range in” should be “takes values in”.
- Page 190: Exercise 1.12.9(e) is significantly harder than intended, as the proof requires Pontryagin duality (which is stated, but not proven, in this text). This part of the exercise should therefore be disregarded. In Exercise 1.12.10, the requirement that
is non-trivial is redundant and may be deleted. For clarity “almost every
” should be “almost every
“. In Exercise 1.12.9(g), “Note that this identification is not unique” should be “We caution that in general, this identification is not unique”.
- Page 194: In the “Unitarity” component of Corollary 1.12.5, “Thus the” should simply be “The”.
- Page 196: In Exercise 1.12.20,
should be
. In Exercise 1.12.21,
should be
.
- Page 197: In Exercise 1.12.24, all occurrences of
should be
.
- Page 198: In the display in Exercise 1.12.25,
should be
. The final word “that” on this page should be deleted.
- Page 200: In Exercise 1.12.33,
should be
.
- Page 201: In the final display of Exercise 1.12.36,
and
should be
and
respectively. Also, in (1.109),
and
should be
and
respectively.
- Page 203: In Exercise 1.12.37, (1.103) should be (1.111).
- Page 209: In the display discussing the FFT, the summation should be over
rather than
.
- Page 214: The topology placed on
given in the paragraph before Exercise 1.13.2 is not suitable for the purposes of this section (it is not locally convex, or even a topological vector space). To fix this, delete the sentence before “Because of this” and replace the next sentence with “We are able to give
a (very strong) topology as follows. Call a seminorm
on
good if it is a continuous function on
for each compact
(or equivalently, the ball
is open in
for each compact
). We then give
the topology defined by all good seminorms. Clearly, this makes
a (locally convex) topological vector space.”
- Page 215: Exercise 1.13.3(iii) is incorrect and should be replaced with the following: “(iii) As an additional challenge, construct a set
such that
is an adherent point of
, but
is not as the limit of any sequence in
.” Exercise 1.13.4(iii) should then be replaced with “Show that a linear map
from the space of test functions into a topological vector space generated by some family of seminorms (i.e., a locally convex topological vector space) is continuous if and only if it is sequentially continuous (i.e. whenever
converges to
in
,
converges to
in
), and if and only if
is continuous for each compact
. Thus while first countability fails for
, we have a serviceable substitute for this property.”. In Exercise 1.13.4 (iv), the constraint
should be
. Exercise 1.13.4 (viii) is trivial and should be deleted. In Exercise 1.13.4(v), the map T needs to be assumed to be linear.
- Page 216: The definition of approximation to to the identity before Exercise 1.13.5 needs to be strengthened, in particular “converge uniformly to zero away from the origin, thus
for all
” should be replaced by “has supports shrinking to the identity, thus for each
,
is supported on
for sufficiently large
“. In Exercise 1.13.5, it would be better to use
rather than
in the hint.
- Page 217: In the second example after Exercise 1.13.7, “Note that this example generalises the previous one” should be “Note that this example generalises the previous one (in the unsigned or absolutely integrable cases, at least)”.
- Page 220: After (1.114),
should be
.
- Page 224: In the third bullet point of Exercise 1.13.25, “some compactly supported distributions” should be “some compactly supported distributions
“.
- Page 225: In the final bullet point of Exercise 1.13.26, “show that
” should be “show that
“, and should also be preceded by a comma.
- Page 227: In Remark 1.13.10, it is the word “both” that should be italicised, rather than “growth”.
- Page 230: In the final display,
should be
.
- Page 232: In Exercise 1.13.37, all the fundamental solutions
are missing a minus sign (this is ultimately due to the refusal to put a minus sign in the definition of the Laplacian, as alluded to on page 229). In Exercises 1.13.38-1.13.40, the Laplacian should be understood to be with respect to the spatial variable
(i.e. it is not the spacetime Laplacian). In Exercise 1.13.38, the factor of
in the definition of
should just be
.
- Page 233: In Exercise 1.13.39, the factor of
in the definition of
should just be
. In Exercise 1.13.40, “wave equation
” should be “wave equation
″, and “Schwartz functions
” should be “Schwartz functions
“.
- Page 238: In the display before Remark 1.14.1, the
symbols should be replaced by
. Similarly for the definition of L after Exercise 1.14.3. In the definition of
, “derivatives of order
” should be “derivatives of order up to
“.
- Page 239: In Exercise 1.14.3,
should be
, and
should be
.
- Page 240: After Exercise 1.14.9, “
is contained in
” should be “
contains
for
“.
- Page ???: In Exercise 1.14.10,
should be
.
- Page 241: In Exercise 1.14.12(2), the additional hypothesis that
is missing.
- Page 242: Exercise 1.14.13 is incorrect and should be replaced by the following: “Let
and
. Show that
is a dense subset of
if one places the
topology on the latter space. (Hint: To approximate a compactly supported
function by a
one, convolve with a smooth, compactly supported approximation to the identity.) What happens in the endpoint case
? “
- Page 242: In Exercise 1.14.14, the signs are reversed in the formulae for
and for
(i.e. there should be a negative sign in the former and a positive sign in the latter, rather than the other way around. Also, in (iii), the formula for
has both a reversed sign and a missing term; it should be
.
- Page 243: In Exercise 1.14.15, Kondrakov should be Kondrachov.
- Page 244: In Exercise 1.14.16,
should be
.
- Page 245: In Exercise 1.14.18, “is
” should be “is the space
of
functions such that the first
derivatives go to zero at infinity”.
- Page 246: In Theorem 1.14.7, “encluding” should be “excluding”.
- Page 248: In Exercise 1.14.20, “of the form” should be “which are something like”, and the annulus should be replaced with a ball. In Exercise 1.4.22, the hypothesis that
is bounded needs to be added.
- Page 249: Before Exercise 1.14.23, “, which we will do in later notes” should be “; see Exercise 1.15.23”. In the last display of Exercise 1.14.21, the
norm should be
instead. (The
case of this exercise is somewhat degenerate, but the result is still true in this case; however, the reader may wish to exclude this case in order to avoid such degeneracy.) Similarly, in the second to last display of the proof of Lemma 1.14.9,
should be
.
- Page 251: in the third paragraph of Section 1.14.3,
should be
.
- Page 253: In Exercise 1.14.34, change “use Schur’s test” to “use the Cauchy-Schwarz inequality or Schur’s test”. The hint in Exercise 1.14.35(i) will not work easily. Instead, substitute: “First prove this when
is a non-negative integer using an argument similar to that in Exercise 1.14.12, then exploit duality to handle the case of negative integer
. To handle the remaining cases, decompose the Fourier transform of
into annular regions of the form
for
, as well as the ball
, and use the preceding cases to estimate the
norm of the Fourier transform of
these annular regions and on the ball.
- Page 254: In the second display of Exercise 1.14.36,
should be
. In the third display,
should be
.
- Page 258: Before (1.125): “chain of maximal ideals” should be “chain of prime ideals”. Bougliand should be Bouligand.
- Page 259: In Section 1.15.1, “k-dimensional subspace” should be “d-dimensional subspace”, and in the second paragraph
should be
throughout.
- page 260: In the fourth bullet point,
should be
. In the last two bullet points,
should be
.
- Page 262: In (1.128) and (1.129), a logarithm is missing in the numerator. In Exercise 1.15.7, the phrase “and any
” should be deleted.
- Page 265: In the first paragraph on this page of Section 1.15.2, “measre” should be “measure”.
- Page 266: In the paragraph before Exercise 1.15.9, “This quantity is increasing in
” should be “This quantity is decreasing in
“.
- Page 267: In the proof of Proposition 1.15.3,
should be
in the definition of
.
- Page 268: In the end of the proof of Lemma 1.15.4,
should be
, and the inequalities
and
should be swapped.
- Page 269: In Exercise 1.15.13,
should be
.
- Page 271: In the proof of Lemma 1.15.7, “Huausdorff” should be “Hausdorff”. In the second bullet point,
should be
. In Exercise 1.15.17, “compact support there” should be “compact support and there”, and “dimension at most
” should be “dimension at least
” (two occurrences); similarly at the end of Lemma 1.15.7.
- Page 273: In Exercise 1.15.20, the measure
should not just be compactly supported, but should be supported in
; and the integrals should be on
rather than
.
- Page ???: Before Theorem 1.8.4,
should be
.
- Page ???: In Definition 1.8.18,
should be
.
- Page ???: In the final paragraph of the proof of Theorem 1.8.23, “
takes” should be “the
take”, and in the final sentence,
should be
.
- Page 286: In the paragraph before 2.2.7, a right parenthesis is missing after “are amenable”.
- Page 287: In the first paragraph of Section 2.2.2, G should be in math mode.
- Page 288: In Lemma 2.2.18, replace the parenthetical with “the existence of which follows from the fact that
can be well-ordered”. In Exercise 2.2.11, the second part does not need to be in red.
- Page 289: In the proof of Proposition 2.2.19, the summation signs in and just after (2.6) should be union signs. Also add the sentence “By incrementing
if necessary, we can take
to be one of the
.”
- Page 290: add a right parenthesis to the end of Exercise 2.2.13.
- Page 291: In the proof of Corollary 2.2.26,
should be
.
- Page 293: In axiom (ii) at the start of 2.3, the second
should be
.
- Page 296: In the proof of Theorem 2.3.4, one of the B’s (in “map B to 1”) should be in math mode.
- Page 298: In the proof of Theorem 2.3.10, omit “one” in “Boolean algebra isomorphism one instead”.
-
Page 299. In Remark 2.3.11: N should be in math mode in “empty interior is in N”.
- Page 303: In (2.14),
should be
. In Exercise 2.4.2,
should be
.
- Page 305: In Proposition 2.4.13, “
and
” should be “
to
“.
- Page 307: In Remark 2.4.22, “Exercises 2.4.3 and 2.4.4” should be “Examples 2.4.6 and 2.4.7”.
- Page 308: In Exercise 2.4.10,
should be
.
- Page 311:In Definition 2.5.1,
should map from
to
, and
should be
.
- Page 317: in the second display after (2.17), the second
should be
.
- Page 319: In the last paragraph of 2.6.1, the term
should be
.
- Page 320: The factors of
should be
, and
should be
.
- Page 333: “whenever the right-hand side is convergent” should be “whenever the right-hand side is absolutely convergent”.
- Page 334: In the proof of (i) implies (ii) in Theorem 2.8.1,
should be
, and “and all
” should be omitted.
- Page ???: In the proof of Proposition 2.8.5, the definition of
should involve
rather than
.
Errata for Vol. II:
- Page 12: “a random complex number in
” should be “a random complex vector in
“.
- Page ???: Just before Theorem 1.4.5,
should contain
rather than
.
- Page 27: In the proof of Theorem 1.4.8,
should be
.
- Page ???: In Proposition 1.5.6, the dimension should be
rather than
.
- Page 40: In the statement of Proposition 1.5.7, a factor of 2 should be inserted in the right hand side, and the dimension should be
rather than
. After that proposition, insert “and dividing into whether
is larger than or smaller than
, and noting also that the claim is trivial for t small” before “…”.
- Page 41: prefactor
should instead be
(and conversely,
should be
), and the final bound of
should instead be
.
- Page 43: In Lemma 1.6.1, add “Let P be a finite set of points in R^2” in the first sentence, and replace “in the plane (which may or may not be in L)” with “in L, plus some additional open line segments not containing any points in P”. In section 1.6.2, “carve out O(r^2) cell” should be “carve out O(r^2) cells”. In the paragraph starting with “To fix the latter problem…”, add “Note that almost surely the open line segments added will not contain any points of P.” after the parenthetical sentence.
- Page 54: 30.7% should be 30.1% .
- Page 82, before (1.53):
should be
.
- Page 90, in the display before (1.61): the final
should be
.
- Page ???: In Section 1.10, “the bits of
on the support of
” should be “the bits of
on the support of
“.
- Page 112: In Remark 1.15.20, “incompleteness theory” should be “incompleteness theorem”.
- Page 177: After (2.19), “existence of a quadratic residue” should be “existence of a quadratic nonresidue”.
- Page 235: The proof of Lemma 2.as stated, because it is not demonstrated that the embedding of the A’ free group into the A group is injective. The proof can be salvaged by constructing the semidirect product first, and then constructing the isomorphism between that product and the free group. Details can be found at this post.
- Page 238: In the last display,
should be added at the end, and similarly for the first display on the next page; in the display after that,
should also be appended.
- Page 310: “all group elements
” should be “all group elements
“.
Thanks to Marcelo Aguiar, Adam Azzam, Ravi Bajaj, Farzin Barakat, Lucas Braune, Yunbai Cao, Nick Cook, Alex Dobner, Kun Dong, Sean Eberhard, Sylvester Eriksson-Bique, Shea Fairchild, Federico, Stephen Ge, Wengyin Gan, Julian Gold, Jordy Greenblatt, Cole Grunniger, Robert Hannah, Matthias Hübner, Joe Hughes, Ahmad Hussein, Ivo, Sune Kristian Jakobsen, Dominik Juestel, Deron Lessure, Zane Li, Dirk Lorenz, Martin Los, Cao Lu, Freddie Manners, Ian Martin, Ricardo Minares, Alexey Muranov, Sujit Nair, Nick, Seungly Oh, John Pearson, Qiang, Yudong Qiu, Rex, James Robinson, Agus Seonjaya, Lior Silberman, August Sonne, Dan Stroock, Jon Susice, Sunting, Yotas Trejos, Bruce Tu, Kent Van Vels, Anthony Verbitsky, Gerd Wachsmuth, Ben Wallis, Joshua Wilson, wilsonofgordon, xuhmath, Sunting Yan, and Yaoliang for corrections.

53 comments
Comments feed for this article
8 February, 2010 at 2:28 pm
An epsilon of room: pages from year three of a mathematical blog « What’s new
[…] Tao I have just finished the first draft of my blog book for 2009, under the title of “An epsilon of room: pages from year three of a mathematical blog“. It largely follows the format of my previous two blog books, “Structure and […]
17 February, 2010 at 12:55 am
גיקדום 17.02.2010 « ניימן 3.0
[…] כבר שלוש שנים, כשכל שנה הוא מייצר ספר מהחומר בבלוג. אז השבוע יצא הספר השלישי, שמדבר על אנליזה מודרנית ברמת הסטודנט, בעיות ברמות של […]
28 September, 2010 at 8:58 am
Ulrich
Terence, any news about the publishing date of this book?
Ulrich
28 September, 2010 at 9:55 am
Terence Tao
We are working on the galley proofs right now. For various reasons the book was delayed by a few months as compared against the previous volume in this series, but hopefully it will still be ready by the end of this year.
21 December, 2010 at 11:21 am
Anonymous
Is the second volume expected to contain the notes from your class on Random Matrix Theory (or are they available in pdf somewhere else?)?
21 December, 2010 at 11:28 am
Terence Tao
This will be part of the 2010 book, which I plan to start working in next month.
21 December, 2010 at 11:30 am
Honglang Wang
coungratulations!
21 December, 2010 at 11:42 am
Timothy
Will you include the article about group extensions in the 2010 book? E.g. who you talked about pixels and zooming in.
3 March, 2011 at 7:59 am
Ulrich
Terence, I am trying since weeks to order the book “A epsilon of room 1” but the book store always get “not available yet”, even Amazon is saying this to me. It is already sold out? If yes, will there be an new printing available?
Regards
Ulrich
4 March, 2011 at 7:54 am
Terence Tao
I received my own copies of the book about a week ago, so it should be currently available.
23 May, 2012 at 6:48 am
Ben
I think in theorem 1.2.4 and corollary 1.2.5 (Lebesgue-Radon-Nikodym) you want f:X -> R measurable, not f:X -> C measurable. If f takes complex values then the measure m_f isn’t going to be defined.
[Corrected, thanks – T.]
27 May, 2012 at 4:53 am
Ben
Thank YOU for the awesome book!
21 January, 2013 at 4:19 pm
Isaac Solomon
On page 49, Exercise 1.4.2 asks one to show that a Hermitian positive semidefinite matrix gives rise to an inner product. Does this require the Hermitian matrix to be positive definite? Thanks.
21 January, 2013 at 4:50 pm
Terence Tao
No, the exercise also works in the semi-definite case also. (Note that the are not required to be linearly independent.) One way to deal with the semi-definite case is to first construct a degenerate inner product in which some elements have norm zero, and then somehow fix the space to eliminate the degeneracy.
are not required to be linearly independent.) One way to deal with the semi-definite case is to first construct a degenerate inner product in which some elements have norm zero, and then somehow fix the space to eliminate the degeneracy.
5 February, 2013 at 8:27 pm
Isaac Solomon
On page 65, in the proof of Hahn-Banach (complex case), it says “optimising in \theta, we see that \tilde{\rho} has norm at most 1”. This seems like a typo, and that it should say “we see that \tilde{\lambda} has norm at most 1”.
[Correction added, thanks – T]
18 February, 2013 at 8:47 pm
Adam Azzam
Minor typo: On Page 103, two lines above Exercise 1.8.4, I believe that “property that for any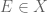 , exactly one of
, exactly one of  and
and  lies in
lies in  ” should instead read “property that for any
” should instead read “property that for any  , exactly one of
, exactly one of  and
and  lies in
lies in  ”
”
[Correction added, thanks – T.]
21 February, 2013 at 9:56 pm
Adam Azzam
I don’t intend to be pedantic, but on the optional part of Exercise 1.8.21 (Page 111), there is no explicit assumption that the space X is first countable [unlike all the other parts, which explicitly state the relevant topological assumptions]. I know is more or less implied since the problem statement introduces the notion of first countability (and is false otherwise), but I thought you might want to be aware of this.
[Correction added, thanks – T.]
4 June, 2013 at 6:39 pm
Yunfeng Zhang
Dear Prof. Tao,
The hint for the first part of Exercise 1.14.20 (Page 282) does not seem to work. I believe that one correct version of a counterexample could be
 with
with  supported on the annulus
supported on the annulus  .
.
4 June, 2013 at 6:50 pm
Yunfeng Zhang
I mean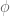 is a nonzero test function which is 1 on
is a nonzero test function which is 1 on 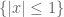 and is 0 on
and is 0 on  .
.
5 June, 2013 at 8:28 am
Terence Tao
Fair enough, the hint should be a bit looser, saying that one should try a function that is “something like” though not exactly this particular function. (Your example works; there are other options too.)
though not exactly this particular function. (Your example works; there are other options too.)
6 June, 2013 at 12:22 pm
Adam Azzam
Minor typo: In the second display equation of Exercise 1.14.36 on Page 254, I believe that should be
should be  .
.
[Correction added, thanks – T.]
7 January, 2014 at 10:54 pm
Adam Azzam
On Page 233, Exercise 1.13.40, I believe what is written “wave equation ” should perhaps be “wave equation
” should perhaps be “wave equation  ″.
″.
[Correction added, thanks – T.]
22 May, 2014 at 6:44 pm
Dimitris Ntalampekos
On this webpage, errata item: page 232, “Exercise 1.13.18” should be “Exercise 1.13.38”.
[Corrected, thanks – T.]
29 February, 2016 at 2:44 am
Jonathan Setinmann
What is the reason for studying complex Hilbert spaces in particular, complex $L_p$ spaces ?
I assume that something similar to basic matrix analysis or complex analysis happens here, where the results from the complex case can succesfully be applied to understand the reals case better (specifically, in the first case the fundamental theorem of algebra makes is compelling to analyse a matrix in the complex domain and then descend the results into the real domain and in the second case real integrals can be succesfully evaluated using methods from complex analysis).
These are the only two instances I know of, that motivate doing the work of extending a given theory (real matrix analysis or real analysis in this case) from the real case to the complex case.
In the case of complex Hilbert spaces, I don’t know of any such application, which makes studying the complex case seem a bit like an idle generalization of the real case. What compelling reasons exist, to take the theory of Hilbert spaces ,in particular the theory of the Lebesgue integral for $[0,+\infty)$- resp. $\overline{\mathbb{R}}$-valued functions, from the real case to the complex one ?
29 February, 2016 at 9:37 am
Terence Tao
One major application is quantum mechanics, which is most naturally phrased on a complex Hilbert space: https://en.wikipedia.org/wiki/Dirac%E2%80%93von_Neumann_axioms
As you note, complex Hilbert spaces also have a much better spectral theorem than their real counterparts, which is something one can already see in finite dimensions, when real normal matrices cannot always be diagonalised (e.g. a rotation matrix in two dimensions) whereas a complex normal matrix always can. Basically, with complex methods one can unify the three major linearised dynamics – exponential growth, exponential decay, and oscillation – into a single dynamic of complex exponentiation (with the qualitative behaviour of the dynamics then determined by whether the spectral parameter has positive real part, negative real part, or is purely imaginary).
Related to this, another major advantage of working with complex-valued function spaces is the ability to cleanly use the Fourier transform: https://en.wikipedia.org/wiki/Fourier_transform . More generally, the theory of Fourier integral operators and pseudodifferential operators, as well as the entirety of microlocal analysis, is best phrased for complex-valued functions.
6 March, 2016 at 11:02 am
Student
It seems that the order how concepts are introduced in the sentences “If $(c_{\alpha})_{\alpha\in A}$ is square-summable, then at most countably many of the $c_{\alpha}$ are non-zero (by Exercise 1.3.4).[…] we can then form the sum $\sum_{\alpha\in A}c_{\alpha}e_{\alpha}$ in an unambiguous manner.”, taken from pp. 55 from the above pdf, is not working. (Or at least I can’t see an immediate way to make them work).
This is because (square-)summability of a sequence, having possibly uncountable terms, is not defined at the point when it is mentioned. This as yet undefined notion of summability then has to be used to show that it can be exchanged with a usual, countable notion of summability (since “most” terms are zero). Also it is not clear, what Exercise 1.3.4, having to do with step functions, has to do with these summability issues.
7 March, 2016 at 12:24 pm
Terence Tao
Square-summability means that the coefficients lie in
lie in 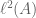 , which is
, which is  with counting measure. This was already constructed even when
with counting measure. This was already constructed even when  is uncountable.
is uncountable.
Note also that Exercise 1.3.4 is distinct from Example 1.3.4.
26 January, 2017 at 12:25 am
Maths student
I have a terminology question: I would think that the name “LCHA group” would be more appropriate than “LCA group”?
26 January, 2017 at 12:45 am
Maths student
And one more thing: On p. 186, it says that Lebesgue measure is a Haar measure (in ptic. a Radon measure), although Lebesgue measure should be defined on more than the Borel algebra?
28 January, 2017 at 9:27 am
Terence Tao
By abuse of notation, the restriction of Lebesgue measure to the Borel sigma-algebra is often also referred to as Lebesgue measure.
28 January, 2017 at 9:26 am
Terence Tao
With the modern definition of compactness, yes; I believe the terminology of LCA group (which is now heavily entrenched) dates back from the Bourbaki era in which “compact” was used to denote what we would now call “compact Hausdorff” (with “quasi-compact” used for what we now call “compact”).
14 March, 2022 at 6:31 pm
Cole Gruninger
In the proof of Proposition 1.15.3 on pg 267, should the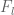 sets be defined as
sets be defined as
rather than
[Erratum added, thanks – T.]
27 March, 2022 at 6:25 am
Anonymous
TAO please in the future can you combine the measure theory book with this one and publish a single ultimate book on real analysis?
Thank you.
29 March, 2022 at 4:29 am
Aditya Guha Roy
Prof. Tao although in section 1.6 you have used the term “isolated points” (in definition 1.6.6) I think you have not defined them anywhere before that portion of the text where it appears.
[Erratum added, thanks – T]
11 April, 2022 at 5:12 am
Kent
I think there is a small typo on the example introducing the counting measure and the normalized counting measures. It is example 1.1.14 on page 7 in the text. I think the denominator of the normalized counting measure should be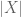 , it is written now as
, it is written now as 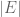 which would result in the normalized counting measure to almost always return unity.
which would result in the normalized counting measure to almost always return unity.
11 April, 2022 at 7:12 am
Kent
I am sorry, I see that this has already been posted as an Erratum. I thought I checked better.
13 April, 2022 at 10:08 am
Kent
I think there might be minor issue with Exercise 1.3.6 on page 35 in the manuscript that is posted online. It the exercise about defining a metric from a norm and that every translation-invariant homogeneous metric arises from a norm.
There is a sentence arises from precisely one norm in this manner” I think I have a counter example. First define a norm
arises from precisely one norm in this manner” I think I have a counter example. First define a norm  by
by  . And define a metric
. And define a metric  by
by  . Then
. Then 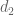 and
and  are both homogeneous and translation-invariant, but they don’t arise from the same norm.
are both homogeneous and translation-invariant, but they don’t arise from the same norm.
“Conversely, show that every translation-invariant, homogeneous metric on
[The question asks to show that each metric arises from a single norm, but does not prohibit the possibility that distinct metrics raise from distinct norms. -T]
19 April, 2022 at 8:52 pm
Kent
I see, that makes sense. Thanks clearing that up for me.
15 April, 2022 at 2:13 pm
Kent
A minor typo, in exercise, 1.4.8 on page 51 in the manuscript posted online, there is a parenthetical statement that doesn’t have a closing parenthesis. It the exercise about completing an inner product space to make a Hilbert space.
[Erratum added, thanks -T.]
15 April, 2022 at 4:16 pm
Kent
Another very minor issue. It is in exercise 1.4.16 on page 54 of the published manuscript. It is the exercise about the properties of Hilbert space adjoints of continuous linear operators. In the second and third bullet points, the various T’s are typeset differently even thought they refer to the same object.
[Erratum added, thanks – T.]
16 April, 2022 at 6:12 am
Kent
I think I have found a small issue with exercise 1.5.10 on page 63 of the manuscript that is posted online. It is the exercise about showing the matrix representation of transpose or linear operation is the “normal” transpose of the matrix. The domain and codomain, are C^n and C^m respectively, and the matrix has dimensions . I think that this is inconsistent. Shouldn’t it be $\latex m\times n$ (Or the domain and codomain could be switched, of cource).
. I think that this is inconsistent. Shouldn’t it be $\latex m\times n$ (Or the domain and codomain could be switched, of cource).
[Erratum added, thanks – T.]
13 June, 2022 at 2:39 pm
Kent
I have a question about the manuscript. On page 53 of the manuscript. There is Remark 1.4.14. This remark makes reference to another remark, Remark 1.26. I am reasonably sure that there isn’t a Remark 1.26 in the text. (The remarks are labelled like (X.Y.Z) ). I suspect that you meant equation 1.26 (on page 40). Is this correct?
Thanks.
[This reference should instead be to Remark 1.3.19. -T]
18 June, 2022 at 10:02 am
Kent
Thank you for clearing that up. The erratum that was posted might be incorrect, though. The reference to Remark 1.26 was in Remark 1.1.14 not Remark 1.1.4. and it was on page 55, not page 53. (At least in my book, I checked a few of the errata and they corresponded to the pages you have posted here so I think I have the correct edition of the book (not the free one I used to use). Thanks.
[Corrected, thanks – T.]
19 June, 2022 at 8:33 am
Kent
On page 209 (of the non-free manuscript) in the paragraph that discusses the discrete (fast) Fourier transform, the formula for the transform has a discrepancy between using and using
and using  . The sum is for
. The sum is for  but the argument of
but the argument of  (and the exponential) is an
(and the exponential) is an  .
.
[Erratum added, thanks – T.]
29 June, 2022 at 12:10 pm
Kent
In exercise 1.5.1 It say “all linear transformations from a finite-dimensional space, to a normed vector space are continuous”. Am I correct in assuming that the domain is vector space equipped with the topology from a norm?
For a counter example, let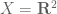 with the trivial (indiscreet) topology and
with the trivial (indiscreet) topology and  (with the usual metric topology), let
(with the usual metric topology), let  be the projection map defined by
be the projection map defined by  . Then it is straight forward to show that
. Then it is straight forward to show that  is not continuous.
is not continuous.
Even with this change I am having a hard time doing the exercise. Suppose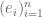 is a basis for
is a basis for  and
and  ,
,  denote the norms on
denote the norms on  and
and  respectively. Then if I define a new norm
respectively. Then if I define a new norm  as
as
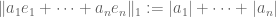 , then I can show that
, then I can show that 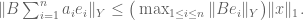 But then I need the fact that my
But then I need the fact that my  norm is at most a constant multiple of the “vanilla”
norm is at most a constant multiple of the “vanilla”  norm to conclude the continuity of
norm to conclude the continuity of  at the origin (and hence the continuity everywhere). This doesn’t seem correct to me because that fact is supposed to be consequence of what we are showing here (part 2 of the question). It seems easier and cleaner to show that all norms on finite dimensional spaces are equivalent first and then use that to show that linear transformations with a finite dimensional domain are continuous.
at the origin (and hence the continuity everywhere). This doesn’t seem correct to me because that fact is supposed to be consequence of what we are showing here (part 2 of the question). It seems easier and cleaner to show that all norms on finite dimensional spaces are equivalent first and then use that to show that linear transformations with a finite dimensional domain are continuous.
Should I use a different approach? I appreciate any help.
30 June, 2022 at 6:30 am
Terence Tao
Yes, in this exercise the finite dimensional space should also be assumed to be normed.
This approach will work. Hint: show that using the topology (i.e., the usual topology), the unit sphere
topology (i.e., the usual topology), the unit sphere  is compact and that the
is compact and that the  norm is continuous and non-zero on this sphere, hence bounded above and below.
norm is continuous and non-zero on this sphere, hence bounded above and below.
1 July, 2022 at 7:12 pm
Kent
Thank you, I see how that works now. I appreciate the response.
11 July, 2022 at 9:44 am
Kent
Hello professor.
I have decent collection of what I think are minor typos in this book. Would you rather I wrote individual messages here for them or gave them to you at once or something else. I want to make sure I don’t “miss the bus” if a new edition of the book is coming out soon.
Please let me know what would be best for you.
[I prefer to have a single list of errata rather than one separate comment for each erratum. -T]
3 April, 2023 at 6:15 am
Aditya Guha Roy
Although it’s understood, I think you might still like to add the definition.
4 April, 2023 at 8:03 pm
Aditya Guha Roy
On page 115 (of print; which is 123 of pdf) on the first line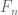 should be
should be 
[Added, thanks – T]
15 December, 2023 at 1:02 am
Shea Fairchild
sorry to bother you, and thank you very much for the inclusion! would it be possible to update ‘gamalf123’ to ‘Shea Fairchild’?
[Done – T.]
29 April, 2024 at 3:50 pm
Anonymous
Hello Professor,
I have a question about the proof of the Riesz representation theorem (Theorem 1.4.13). We have a functional for which we want to construct a vector that “acts the same way”.
for which we want to construct a vector that “acts the same way”.
Anyways, the proof constructs the vector but makes a choice of a vector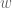 from the orthogonal complement of the null space of
from the orthogonal complement of the null space of  . It seems like we need to show that the vector we define is independent of the choice of
. It seems like we need to show that the vector we define is independent of the choice of 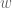 . Or is this a moot point because we already have uniqueness?
. Or is this a moot point because we already have uniqueness?
Thank you,
Kent Van Vel
10 May, 2024 at 8:16 pm
Terence Tao
For the purposes of establising existence, independence of the choice of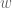 is not needed. As you note, in this proof we are establishing existence and uniqueness separately.
is not needed. As you note, in this proof we are establishing existence and uniqueness separately.