Last updated: Feb 18, 2023
Poincaré’s legacies: pages from year two of a mathematical blog (Volume I, Volume II)
Terence Tao
American Mathematical Society
Volume I: ISBN-10 0-8218-4883-6, ISBN-13 978-0-8218-4883-8
Volume II: ISBN-10 0-8218-4885-2, ISBN-13 978-0-8218-4885-2
This is a sequel to “Structure and Randomness: Pages from year one of a mathematical blog“, in two volumes.
A draft version of the MS can be found here (note that the printed version will have substantially different page and section numbering, in particular being split into two volumes).
The front cover for the first volume is here, and for the second volume is here.
See also this blog announcement.
— Errata for the first volume —
- Page 9: In Section 1.3, the sketch of proof of Green’s theorem (Theorem 1.3.7) has a serious gap; the problem is that the quotiented orbit of
may possibly have a constant image with respect to a horizontal character. It seems that to use this type of argument to obtain the full strength of Theorem 1.3.7 (and not just some special cases) one needs the more complicated quantitative van der Corput argument from [GrTa2009c].
- Page 21: In the first display after (1.19),
should be
.
- Page 23: In (1.23),
should simply be
.
- Page 24: After (1.30),
should be
.
- Page 25: In (1.32), (1.33), (1.34),
should be
.
- Page 27: In (1.37),
should be
.
- Page 64: In the two long displays the symbol P is missing just before the right bracket ] on most of the lines of the displays.
- Page 69: In the final paragraph, “
-chain” should be “
-chain”.
- Page 70: In the final display,
should be
. In the final paragraph, “
-cocycles and
-cochains” should be “
-cocycles and
-boundaries”.
- Page 76: In Example 2.1.3, delete the parenthetical reference to Example 2.1.1.
- Page 87: In Exercise 2.2.4, the last sentence should be phrased as a question, i.e. “Does there exist analogous claims in the categories of dynamical systems and measure-preserving systems?”.
- Page 90: In the proof of Lemma 2.3.3, add “By passing to a subsequence and relabeling, we may assume
converges to
” before “But then one verifies…”.
- Page 95: Remark 2.3.7 is inaccurate regarding the left-continuity of
(see this paper for the subtle issues arising here) and should be deleted.
- Page ???: In Exercise 2.13.4,
should be
.
- Page 99: Exercise 2.4.5 is not relevant at this juncture and should be deleted.
- Page 102: in the proof of Proposition 2.4.11,
should lie in
rather than
. In particular, the parenthetical remark about setting
equal to
should be deleted.
- Page 104: In the proof of Lemma 2.4.13,
should be
.
- Page 110: A similar ultrafilter proof also appears in Section 3 of N. Hindman’s paper “Problems and new results in the algebra of Beta S and Ramsey Theory” in “Unsolved problems on mathematics for the 21st century”, J. Abe and S. Tanaka eds., IOS Press, Amsterdam (2001), 295-305.
- Page 113: Lemma 2.5.14 should be called the Ellis-Numakura lemma rather than the Ellis-Namakura lemma. (Similarly for the index entry for this lemma.)
- Page 127: In Definition 2.6.16, it should be stressed that the fibre metrics
are compatible with (i.e. generate) the topology on the fibres inherited from the full space. (More generally, in this text, when we refer to a metric on a topological space, it should be understood that that metric generates the topology of that space unless otherwise specified.)
- Page 128: In the first paragraph,
should be
.
- Page 132: In Lemma 2.6.30,
should be
.
- Page 134: In Example 2.7.2,
should be
, and
should be
.
- Page 135: In Exercise 2.7.2(5), it should be explicitly stated that X is assumed to be distal.
- Page ???: In Exercise 2.7.6(3),
should be
.
- Page 137: After Exercise 2.7.8, the reference to Exercise 2.7.5 should be to Exercise 2.7.3 instead.
- Page 139: After (2.54), W should be K.
- Page 141: Exercise 2.7.14 is the same as 2.9.13 and should be deleted.
- Page 143: The last sentence of the proof of Theorem 2.8.2 is redundant and should be deleted. In Exercise 2.8.3,
should read
(two occurrences), and “any smaller” should be “any larger”.
- Page 144: The first proof of von Neumann’s ergodic theorem is due to F. Riesz, rather than von Neumann, and the text should be edited accordingly. After (2.63), “uniformly in
” should be “uniformly in
“. Also
should be
.
- Page 146: After (2.67),
should be
.
- Page 149: In Exercise 2.8.6(1), “
-valued” should be $latex {\mathcal X}-measurable”.
- Page 150: In Exercise 2.8.9, Corollary 2.8.12 should be Corollary 2.8.16.
- Page 152: In Theorem 2.9.1, in the definition of
, the summation should be from
to
, rather than from
to
.
- Page 153: In the first display, the equality sign should be a
sign instead.
- Page 157: In Exercise 2.9.6, the probability space should be assumed to be standard Borel (in order to define the countable product space properly).
- Page 158: In the first paragraph of Section 2.9.4, “Borel
-algebra of
” should be “Borel
-algebra of
“. In Exercise 2.9.10, “measure on
” should be measure on
“. For Exercise 2.9.9, “if and only if” should just be “only if”, and the additional hypothesis that
has a boundary of measure zero should be added.
- Page 159: In Exercise 2.9.13, one needs to add the additional hypothesis that the support of the invariant measure
is equal to the whole space
.
- Page 160: In Example 2.9.17, “from
to
and from
to
” should be “from
to
and from
to
“. Also, all integrals here should be over Y rather than over X.
- Page 162: In the right-hand side of (2.96), the factor
should be moved outside the inner integral (for clarity). In Exercise 2.9.14,
should be
.
- Page 163: In the final parenthetical of Exercise 2.9.15, add “, but I do not know of a way to prove Proposition 2.9.22 in full generality just from Choquet.”
- Page 167: After (2.100), the range
should be replaced with
.
- Pages 189, 194: In Exercise 2.12.15, and also in the first paragraph of Section 2.12.4, Corollary 2.12.8 should be Corollary 2.12.13. After Remark 2.12.24, Proposition 2.12.15 should be Proposition 2.12.14.
- Page 190: In footnote 44 in Theorem 2.12.14, “always has full measure” should be “always has full (outer) measure”.
- Page 191: Replace the first sentence in the paragraph preceding 2.12.17 by “Given a Hilbert space H, define its complex conjugate
to be the set of formal conjugates
of elements of
, with the addition structure
, the conjugated scalar multiplication structure
and the conjugated inner product
.”. In equation (2.130),
should then be
, and the second inner product should be subscripted by
.
- Page 195: In Exercise 2.12.22,
should be
.
- Page 203: In (2.159), the
term is unnecessary, and (2.151) and”and relative Cauchy Schwarz again” may be deleted from the preceding line. After (2.160), the parenthetical remark can be deleted, and after (2.161), “again” may be deleted.
- Page 207: In (2.168), the second
should be
.
- Page 208: the integration
is missing from the summand.
- Page ???: In Remark 2.14.4, the hypothesis that
is ergodic needs to be added.
- Page 210: In Proposition 2.14.11, the “weak operator topology” should be clarified to “the weak operator topology of
“, and it should also be parenthetically noted that the
are uniformly bounded in the Hilbert space
. In the statement of this proposition, “technology” should be “topology”. In Definition 2.14.13,
should be
.
- Page 216: After (2.188), “on a set of measure
” should be “outside of a set of measure
“.
- Page 218: In Exercise 2.16.1(7), “H/[H,K] and K/[H,K] become abelian” should be “the images of H and K become groups that commute with each other”.
- Page 221: In Example 2.16.9,
should just be
.
- Page 222: In Example 2.16.13, the group element g should have a coefficient of -1 instead of 1 in the third column, second row position.
- Page 223: In (2.203),
should be
.
- Page ???: The statement and proof of Corollary 2.16.21 and Corollary 2.16.22 need to be modified, because the character
in the proof of the former need not be primitive. In Corollary 2.16.21(2), one needs to partition the orbit
into finitely many suborbits
for various congruence classes
before the claim holds separately for each suborbit, and similarly for Corollary 2.16.22.
- Page 231: The proof of Lemma 2.17.5 is incomplete, because U and D do not fully generate
. To finish the argument, observe that
converges to the identity as
, and thus
. Using the D-invariance we conclude that
, and thus as before v is also invariant with respect to the group U’ generated by the
. Since U and U’ (and D, if desired) generate
, the claim follows.
- Pages 232-233: The proof of Lemma 2.17.9 requires some changes. In the penultimate paragraph, “any g in L” should be “any g in L with
sufficiently close to
“. The final paragraph needs to be changed to the following: “Suppose that
is not closed; then one can find a sequence
in
that converges to
but with the
staying bounded away from the identity for
. For a sufficiently small compact neighbourhood
of the identity in
, the sets
then are disjoint and all have the same measure for
large enough; since
, this forces these sets to be null. But then the invariant measure
annihilates
and is thus null as well, a contradiction.”
- Page 235: In Proposition 2.17.12,
should lie in
rather than
. In the proof of that proposition,
should be
.
— Errata for the second volume —
- Page ???: In Footnote 36,
should be
.
- Page 40: After (1.17), “multiply
by a scalar” should be “multiply
by a scalar”. Two pages previously, the display for U+E has an extraneous space. In (1.18), all appearances of
and
should be
and
instead.
- Page ???: In example (8) of Section 1.4,
should be
.
- Page 67: Before (2.11),
should be
.
- Page 71: In (2.29),
should be
.
- Page 74: In Definition 2.1.14 II,
should be $X^\alpha Y^\beta$.
- Page 77: Before (2.38): the heat equation
should be
.
- Page 78: In the second line of (2.45), the first negative sign should be positive, and the positive sign should be negative. In (2.48), the last two minus signs should be plus signs, and in (2.49),
should be
.
- Page ???: In the discussion before (2.53), the manifold should be complete in addition to smooth and connected.
- Page 81: After (2.60), $latex\phi^*(t) \dot \phi(t)$ should be
.
- Page ???: In (2.67),
should be
.
- Page 115: In (2.121),
should be
.
- Page 127: In (2.143), the factor of
should be deleted.
- Page 132: In (2.162),
should be
.
- Page 136: After (2.170), “slows down the flow of time by
” should be “slows down the flow of time by
“.
- Page 152: On the last line, (2.72) should be (2.73).
- Page ???: In Exercise 2.9.4,
should be
.
- Page ???: In (2.247),
should be
.
- Page ???: In (2.264),
should be
; in (2.266),
should be
. In (2.274),
should be
.
- Page 160: Strictly speaking, the derivation given of the log-Sobolev inequality is only valid for those
for which
is the backwards time evolution of a non-negative test function
by the backwards heat equation for time
. However, if one runs the argument with
the backwards evolution of
starting from time
, rather than starting from time 0, one obtains the log-Sobolev inequality for all test functions
. On the penultimate line, (2.239) should be (2.246).
- Page 175: In the second line,
should be
.
- Page ???: In equations (2.303)-(2.305),
should be
.
- Page 191: In (2.328), the two
signs should both be
.
- Page 205: “manifild” should be “manifold”.
- Page 213: In (2.416) and immediately afterwards,
should be
.
- Page 217: In the sentence after (2.437), “every
” should be “every
“.
- Page 229: The formulation of the Hamilton compactness theorem given here needs an additional hypothesis, namely a uniform lower bound on the Ricci curvature. More precisely, for any compact interval J there exists a K such that for every radius r one has
on
for all sufficiently large n. This is needed to prevent the length of a geodesic going off to infinity from collapsing to a finite length, causing incompleteness. (It was recently shown by Topping that the formulation of the compactness theorem give in the text can fail without such a hypothesis. However, in the applications to the Poincare conjecture one has the uniform lower bound on curvature, so this is ultimately not a major issue.)
- Page 234: In Corollary 2.16.11,
should be
.
- Page 257: Before Proposition 2.18.15, the final “oriented” should be “unoriented”.
- Page 263: In the sketch of proof of Proposition 2.19.9,
should be
.
- Page 270: “width of the necks goes to infinity” should be “width of the necks goes to zero”.
- Page 290: The reference [Zhang2007] should be “Zhang, Qi S., Strong noncollapsing and uniform Sobolev inequalities for Ricci flow with surgeries. Pacific J. Math. 239 (2009), no. 1, 179–200”.
Thanks to Ian Biringer, Terry Bollinger, Fransisc Bozgan, Tim Carson, Rex Cheung, Paul-Olivier Dehaye, Daoyuan Han, Neil Hindman, Asgar Jamneshan, Abhishek Khetan, Ioannis Kontoyiannis, Sajjad Lakzian, James Leng, Jeff Lin, Jun Ling, Xiaochuan Liu, Freddie Manners, Mizar, Ramis Movassagh, Hee Oh, Oskar, Pavel, Robert Tu, Siming Tu, Mate Wierdl, Yifan, Qi Zhang, Yunfeng Zhang, Tamar Ziegler, Yuming Zhang, Pavel Zorin, and an anonymous commenter for corrections and references.

15 comments
Comments feed for this article
23 November, 2008 at 3:53 pm
Structure and Randomness: pages from year one of mathematical blog « What’s new
[…] will form the bulk of that book, I have chosen the working title for that book to be “Poincaré’s legacies: pages from year two of a mathematical blog“. Possibly related posts: (automatically generated)Setting things up…The blog bookMy […]
23 November, 2008 at 6:34 pm
Jonathan Vos Post
I look forward to this… and I’m sure that many others do, as well.
31 July, 2009 at 9:23 pm
Manjil P. Saikia
Dear Prof. Tao,
Where can I get this book in India?
3 August, 2009 at 8:46 am
nightninja
Hey Professor Tao,
There isn’t any plans to get this on kindle is there?
8 February, 2010 at 2:28 pm
An epsilon of room: pages from year three of a mathematical blog « What’s new
[…] 7 February, 2010 in Mathematics, book | Tags: mathematical blogging | by Terence Tao I have just finished the first draft of my blog book for 2009, under the title of “An epsilon of room: pages from year three of a mathematical blog“. It largely follows the format of my previous two blog books, “Structure and Randomness“ and “Poincaré’s legacies“. […]
6 December, 2014 at 4:48 pm
Lam
Dear Terry,
On p.214, in the proof of Proposition 2.15.6, you say
“by monotone convergence, we can find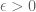 such that
such that  for all
for all  outside of a set
outside of a set  of measure at most
of measure at most  .”
.”
If the support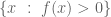 has measure
has measure  , shouldn’t the set
, shouldn’t the set  have smaller measure?, so its complement should have greater measure than
have smaller measure?, so its complement should have greater measure than 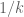 ? I am not sure I understand the argument.
? I am not sure I understand the argument.
Thanks!
6 December, 2014 at 9:40 pm
Terence Tao
The support has measure strictly greater than
has measure strictly greater than  , hence greater than
, hence greater than  (say) for some
(say) for some 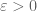 .
.
27 July, 2018 at 7:26 am
Maths student
Dear Prof. Tao,
after waking up from a sleep at noon, I found that in example 2.2.10, “minimal” should read “not minimal”.
W/BR
27 July, 2018 at 7:28 am
Maths student
(Technically, also an integer can’t be a vector, but this seems too trivial to report; I don’t think my previous post is a waste of your time, but this one may be.)
27 July, 2018 at 8:37 pm
Terence Tao
I believe the example is correct as it stands. For instance, when , the system is very far from minimal, and also
, the system is very far from minimal, and also  for every non-zero
for every non-zero  . (Note that the dot product of two vectors is a scalar, not a vector, so it makes sense to ask whether it is an integer or not.)
. (Note that the dot product of two vectors is a scalar, not a vector, so it makes sense to ask whether it is an integer or not.)
28 July, 2018 at 4:53 am
Maths student
Ah, I thought this was a topological dynamical system. Because then, if we think of the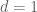 case, the closure is everything. I also thought one would start at a specific
case, the closure is everything. I also thought one would start at a specific  , which was my main mistake. (Even then, for minimality the periodicity would not suffice, because
, which was my main mistake. (Even then, for minimality the periodicity would not suffice, because  might not be prime. Anyway.)
might not be prime. Anyway.)
Another thing: In (2.6) I’m having trouble to see that the limit exists, though we don’t need it; we could pass to the lim inf, because we don’t need equality, only “grequality”. We could also pass to a subsequence and name it the same.
28 July, 2018 at 4:58 am
Maths student
Note: Above I indicated another correction.
28 July, 2018 at 6:27 am
Maths student
I mean, another supposed correction.
28 July, 2018 at 8:48 am
Terence Tao
Thanks for the additional correction. But regarding the torus shift, I am indeed thinking of this system as a topological dynamical system. In the one-dimensional case, for instance, the orbit of a shift
of a shift  in the unit circle
in the unit circle 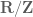 will be dense precisely when
will be dense precisely when  is irrational. (The higher-dimensional statement is basically Kronecker’s theorem.)
is irrational. (The higher-dimensional statement is basically Kronecker’s theorem.)
28 July, 2018 at 10:41 pm
Maths student
Dear Prof. Tao,
I had not the least doubt. (I’m sorry when my corrections are not always accurate, I’m trying to help. I will henceforth start to double check my amendments.)