Tamar Ziegler and I have just uploaded to the arXiv our paper, “The inverse conjecture for the Gowers norm over finite fields via the correspondence principle“, submitted to Analysis & PDE. As announced a few months ago in this blog post, this paper establishes (most of) the inverse conjecture for the Gowers norm from an ergodic theory analogue of this conjecture (in a forthcoming paper by Vitaly Bergelson, Tamar Ziegler, and myself, which should be ready shortly), using a variant of the Furstenberg correspondence principle. Our papers were held up for a while due to some unexpected technical difficulties arising in the low characteristic case; as a consequence, our paper only establishes the full inverse conjecture in the high characteristic case , and gives a partial result in the low characteristic case
.
In the rest of this post, I would like to describe the inverse conjecture (in both combinatorial and ergodic forms), and sketch how one deduces one from the other via the correspondence principle (together with two additional ingredients, namely a statistical sampling lemma and a local testability result for polynomials).
— Polynomials and the Gowers norm —
Let F be a finite field, and let be a vector space over that field. Given any function
taking values in the unit circle
, we define the additive derivative
of P in the direction h by the formula
.
Now let . A function
is said to be a polynomial of degree
if one has
for all
. Thus for instance, the only polynomial of degree <0 is the zero function, the only polynomials of degree <1 are the constants, the only polynomial of degree <2 are the affine characters, and so forth. If
is a field of prime order, and we make the additional assumption that P takes values in the
roots of unity (which we can identify with F in the usual manner), then we can express the polynomial P in the customary manner as
(1)
for some coefficients ; let us refer to these as classical polynomials of degree <k. However, if one does not require P to take values in
roots of unity, then the above definition also encompasses some non-classical polynomials. For instance, if
, the function
defined by P(0)=0 and P(1)=1/4 is of degree <3 (i.e. is a “quadratic” polynomial), but is not classical. [However, it is a nice exercise to show that in the high characteristic case
, every polynomial of degree
can be expressed as the sum of a classical polynomial and a constant; thus the genuinely non-classical polynomials are a purely low characteristic phenomenon. I may write more about the relationship between classical and non-classical polynomials in a future post.]
We can define multiplicative analogues of the above concept. Given a function , we define the multiplicative derivative
to be the function
and say that f is a phase polynomial of degree <k if for all
. It is not hard to show that f is a phase polynomial of degree <k if and only if
for some polynomial
of degree <k, where
is the standard character
.
The Gowers uniformity norms are a means to measure the extent to which an arbitrary function behaves like a phase polynomial; if
, they are defined by the formula
where denotes the average of f on A. Thus, for instance, if f is bounded in magnitude by 1, then
is a number between 0 and 1, and equals 1 if and only if f is a phase polynomial of degree <k.
We have just seen that exact extremisers of the Gowers norms are given by phase polynomials. This statement is in fact robust, in that near-exact extremisers of the Gowers norms are close to phase polynomials:
Theorem 1 (local testabilty of phase polynomials) Suppose that
is bounded in magnitude by 1 and obeys the bound
. Then there exists a phase polynomial g of degree <k such that
, where
denotes a quantity that goes to zero as
for fixed k, F, uniformly in the choice of f or n.
This fact is essentially due to Alon, Kaufman, Krivelevich, Litsyn, and Ron; their paper is focused on the case when and P is a classical polynomial, but it is not too difficult to extend the result to the generality of Theorem 1 (this is done in an appendix to our paper, as we need this local testability result in our arguments). One consequence of this theorem is that one can test (with high confidence) whether a given function is close to a phase polynomial of degree <k, by randomly computing some derivatives
and seeing whether they are consistently close to 1. Note that this test is local, in the sense that one only has to evaluate f at a bounded number of positions in
(even as
) in order to perform the test.
Theorem 1 describes what happens when a function “behaves like a phase polynomial 99% of the time”, in the sense that the Gowers norm is very close to 1. The inverse conjecture for the Gowers norm addresses the more general case in which a function “behaves like a phase polynomial 51% of the time”, in the sense that the Gowers norm is bounded below by some small constant . (Note that if
and
was a random boolean function, then
would equal +1 about 50% of the time and -1 for the other 50%, leading to a very small Gowers norm.) More precisely, we have
Inverse Conjecture for the Gowers norm over finite fields. Let
be a function bounded in magnitude by 1 such that
. Then there exists a phase polynomial g of degree <k such that
for some
independent of n.
This conjecture has a number of applications to the structural theory of additive patterns (e.g. arithmetic progressions) in subsets of ; see for instance this paper of Gowers-Wolf. It is also connected to various problems in computer science, such as generation of pseudorandom bits (see e.g. this paper of Bogdanov-Viola), and to polynomiality testing (see e.g. this paper of Samorodnitsky-Trevisan).
Previously, this conjecture had been verified for by Samorodnitsky (in even characteristic) and by Ben Green and myself (in odd characteristic). In high characteristic
, a partial result (assuming that f was already a classical polynomial of bounded degree) was obtained by Ben and myself; but in low characteristic, it was discovered in that paper and simultaneously by Lovett-Meshulam-Samorodnitsky that the conjecture can fail if one restricts g to be a classical phase polynomial. Nevertheless we believe the conjecture should still in the low characteristic case hold if we allow g to be non-classical.
Our main results are as follows:
Theorem 2. The inverse conjecture is true in the high characteristic case
.
Theorem 3. In general characteristic, a weaker form of the inverse conjecture is true, in which we allow g to be a phase polynomial of degree
rather than
, for some C(k) depending only on k.
As mentioned above, we expect that we should be able to take C(k)=k in any characteristic, but this seems to require a delicate algebraic analysis and we were not able to establish it here.
— Ergodic theory —
We were able to deduce the combinatorial results in Theorems 2, 3 from ergodic analogues of these results. Roughly speaking, these ergodic results correspond to “local” versions of the “global” theorems in Theorem 2, 3, because they involve averaging over only a small portion of the underlying space, as opposed to the global averages used to define the Gowers norms. [In this regard, the ergodic theory results are weaker than the combinatorial ones. However, there is another direction in which the ergodic results are stronger, in that they encode some additional “measurability” information that is not present in the combinatorial setting; roughly speaking, this information asserts that the function g appearing in the above conjecture can be “locally reconstructed” from f in some sense, as opposed to merely existing in some non-constructive sense.] Fortunately, thanks to some “local-to-global” principles (including the local testability result in Theorem 1), we are able to pass back and forth between the two types of theorems in a fairly “soft” manner.
Whereas the combinatorial results take place in the finitary setting of a finite-dimensional vector space , the ergodic theory results take place in the infinitary setting of a probability space
with a measure-preserving action
of the countably infinite vector space
. Given a measurable function
, one can define multiplicative derivatives
for , and we say that f is a phase polynomial of degree <k if
a.e. for all
. We can also define the Gowers-Host-Kra uniformity seminorm
for
by the formula
it can be shown that the limits exist and that this is indeed a seminorm. Thus for instance, as in the combinatorial setting, phase polynomials of degree <k have a Gowers-Host-Kra seminorm of 1.
There is an analogue of the inverse conjecture:
Ergodic Inverse Conjecture for the Gowers norm over finite fields. Suppose that X is ergodic. Let
be such that
. Then there exists a phase polynomial g of degree <k such that
.
In a forthcoming paper of Bergelson, Ziegler, and myself, we show
Theorem 2′. The ergodic inverse conjecture is true in the high characteristic case
.
Theorem 3′. In general characteristic, a weaker form of the ergodic inverse conjecture is true, in which we allow g to be a phase polynomial of degree
rather than
, for some C(k) depending only on k.
The aim of the current paper is to deduce Theorems 2, 3 from Theorems 2′, 3′ respectively.
— Outline of proof —
The main idea here is to use the compactness and contradiction argument as embodied in the Furstenberg correspondence principle (which was discussed in my previous blog post). Suppose for instance that Theorem 2 failed; then one would have a sequence of bounded functions (where
is going off to infinity) with Gowers norms of order k uniformly bounded from below, but such that
becomes increasingly orthogonal to all phase polynomials of degree <k. The idea is then to exploit weak compactness to take a “limit”, which would be a bounded measurable function
on some measure space X with an
action.
The problem in doing this is that the convergence given by weak compactness is only in the “weak” or “local” sense; for instance, one can establish convergence results for local statistics, e.g.
for any fixed , but one cannot immediately establish convergence results for global statistics, e.g.
(2)
for the limit objects X, f obtained by the traditional Furstenberg correspondence principle. To get around this, we first “shuffle” each of the original spaces by a randomly chosen general linear transformation before applying the correspondence principle argument (actually, to be more precise, we pull back
to
using a random linear transformation from the latter to the former, but never mind this technical detail). The point of doing this shuffling is that it makes local averages approximate global averages with high confidence, for exactly the same reason that random polls with moderately large sample sizes can be accurate even when the overall population is enormous (see my previous post for more discussion on this). To cut a long story short, this shuffling (or “statistical sampling”) enables one to obtain convergence results such as (2). This serves several useful purposes in our paper. For instance, it allows us to ensure that the limit system X is ergodic. But more importantly, it allows us to carry the information that each
has large Gowers norm into the limit, concluding that f has large Gowers-Host-Kra seminorm. Thus we are now in a position to apply the hypothesis Theorem 2′ (or Theorem 3′, if the objective is to prove Theorem 3) and conclude that f correlates with a phase polynomial g.
Now we want to pass back from the limit system to the original finitary systems and conclude the desired contradiction. A new problem emerges: the nature of the convergence of the latter to the former allows one to relate (local) statistics of to (local) statistics of
(which in turn relate to global statistics of
), but says nothing about g. Fortunately, the ergodic inverse theorems tell us that g is measurable, which turns out to imply that g is “nearly local” in the sense that it can be approximated to arbitrary accuracy as some function g’ of finitely many shifts of f, which is almost a phase polynomial and will continue to correlate with f if the approximation is good enough. This latter object can be passed back to the original finitary systems, creating functions
correlating with
which are also almost polynomials. To finish off the proof, we use the local testability (Theorem 1) to approximate
by a genuine phase polynomial; this means that the
do, after all, have significant correlation with a phase polynomial, contradicting our hypothesis and establishing the result.
It is tempting to try to use this type of argument to handle the inverse conjecture for the Gowers norm on the integers , especially since ergodic inverse conjectures in this setting are already known thanks to the work of Host-Kra (and also Ziegler). However, there are two non-trivial obstacles here. Firstly, one cannot “shuffle” the integers (or related objects, such as cyclic groups
) with the same degree of freedom as one can for a vector space, causing a difficulty in relating local and global statistics. Secondly, whereas polynomials are known to be local testable, the local testability of the analogous object for the integer case, namely that of nilsequences, is unknown. These difficulties do not appear to be totally insurmountable, but they would require some additional effort to resolve.

13 comments
Comments feed for this article
2 November, 2008 at 6:17 am
JSE
Ah, this puts in context the interesting questions Tamar was asking me about “fake polynomials,” (which I guess in this context have the classier name of “non-classical”) in situations where the degree is larger than the cardinality of the finite field. The problem of classifying these guys really does seem interesting, and perhaps hard. By “perhaps hard” I guess I mean “I have no idea how to do it, but I don’t see a conceptual barrier to someone having an immensely clever idea and just knocking it off somehow.” In this sense, though, it reminds me of the affine cap problem, which also tantalizes the algebraic geometer with the hope that it’ll yield to one clever idea, and which, so far, hasn’t.
So let me see if I understand: when you say
“Nevertheless we believe the conjecture should still in the low characteristic case hold if we allow g to be non-classical.”
do you mean to say, independent of any connection with classical polynomials (i.e. degree-k subvarieties), there should be a theorem that says “if f fails equidistribution in the Gowers norm sense by 1%, f is correlated with something which is maximally badly distributed in the Gowers norm sense?”
2 November, 2008 at 10:14 am
Terence Tao
Dear Jordan,
Yes, this is what we believe to be true. (It is already known to be true in the case of 99% non-equidistribution, as mentioned above.) I plan to post a bit more on these “non-classical” polynomials later; I think they aren’t as mysterious as, say, the capsets, because they already obey a very strong algebraic condition (their iterated derivatives always vanish) and so should be able to be studied by algebraic tools. Incidentally, a good example to keep in mind of such a polynomial is the function on
on 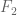 , where
, where 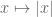 is the obvious map from
is the obvious map from 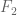 to
to 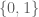 . It’s a nice exercise to see inductively that
. It’s a nice exercise to see inductively that  is a non-classical polynomial of degree
is a non-classical polynomial of degree 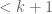 (thus
(thus  is linear,
is linear, 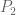 is quadratic, etc.). So I guess this corresponds to the “non-classical algebraic variety”
is quadratic, etc.). So I guess this corresponds to the “non-classical algebraic variety”  .
.
We are able to show that any non-classical polynomial of degree <k in a field of characteristic p is also equal to a function of C(k,p) classical polynomials of degree <C(k,p) for some C(k,p) depending in an explicit fashion on k and p, so non-classical algebraic varieties are also classical algebraic varieties of somewhat higher degree. (For instance, in the above example, if we expand in binary as
in binary as 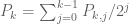 for
for 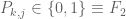 , then each
, then each  is a classical polynomial of degree C(k,j) for some explicit C(k,j) independent of n.)
is a classical polynomial of degree C(k,j) for some explicit C(k,j) independent of n.)
5 November, 2008 at 2:34 pm
Anonymous
I like the new banner Terry.
-Erik
[NB: the banner was intended for one day only, and has now reverted. -T.]
6 November, 2008 at 3:41 am
Anonymous
too bad, it was awesome :)
(the new banner that is)
jon
19 January, 2009 at 10:46 am
An inverse theorem for the uniformity seminorms associated with the action of F^infty_p « What’s new
[…] the action of “. This paper establishes the ergodic inverse theorems that are needed in our other recent paper to establish the inverse conjecture for the Gowers norms over finite fields in high characteristic […]
12 April, 2009 at 5:33 am
real estate
I happened upon your blog and was fascinated with the theorem and proof.
Can you, if you would be so kind, illustrate to a layman such as myself the potential practical applications of this theorem.
Or is it more in the way of a cerebral exercise rather than practical. Please excuse my ignorance but this level of maths is well beyond me
12 April, 2009 at 10:13 am
Terence Tao
Dear real estate,
These results are more in the area of pure mathematics than applied mathematics – they aim to improve one’s general understanding of a mathematical phenomenon (in this case, a form of pseudorandomness called “Gowers uniformity”). A secondary aim here is also to get better at transferring the powerful techniques of ergodic theory to attack combinatorial problems, a strategy which has proven quite fruitful in the past but is still not as fully exploited as I believe it could be.
However, there are some applications which are related to these results. Bogdanov and Viola observed that a variant of this result allows for a new construction of pseudorandom strings of bits that can be efficiently generated, and which are guaranteed to “look random” with regard to any “polynomial test”.
There is also a corresponding inverse conjecture for the Gowers norm over the integers (which is not yet completely proven), which would imply, among other things, some rather precise asymptotic statements about the number of solutions to a variety of linear equations involving primes, see
15 April, 2009 at 6:33 pm
Iverson
Dear Terry:
Last time, i read your and Green’s paper, you obtain the asymptotic value of the progression in prime under the assume Mn(s) and GI(s), it is great and beatuiful result. And the Mn(s) is solved, whethe GI(s) is more difficlut than Mn(s), and the recent paper you with Ziegler or with Bergelson solve the case in the finite filed or the case of the original GI(s)?
22 September, 2009 at 11:30 am
Ryan O'Donnell
This recent paper of Haramaty and Shpilka contains several interesting new results in the same vein:
http://eccc.hpi-web.de/report/2009/080/
24 December, 2011 at 11:31 am
Szemerédi’s regularity lemma « Disquisitiones Mathematicae
[…] are still being developed to generate what is being called higher-order Fourier analysis. See this post of Terence Tao for a discussion about this topic. Going back to what matters, let’s prove the Proposition 10 […]
23 July, 2015 at 7:33 pm
Deducing a weak ergodic inverse theorem from a combinatorial inverse theorem. | What's new
[…] the ergodic inverse theorem by a variant of the Furstenberg correspondence principle, as worked out by Tamar Ziegler and myself, however in the current context of -actions, the connection is less […]
27 May, 2022 at 2:13 pm
Notes on inverse theorem entropy | What's new
[…] field of prime order (so that ), then the inverse theorem of Ziegler and myself (available in both high and low characteristic) allows one to obtain an -inverse theorem for some and the collection of […]
10 March, 2023 at 9:00 am
A Host–Kra ${bf F}^omega_2$-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the $U^6({bf F}^n_2)$ norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse th
[…] compared to . One approach to this theorem proceeds via ergodic theory. Indeed it was observed in this previous paper of Ziegler and myself that for a given choice of and , the above theorem follows from the following ergodic […]