In the previous set of notes, we constructed the measure-theoretic notion of the Lebesgue integral, and used this to set up the probabilistic notion of expectation on a rigorous footing. In this set of notes, we will similarly construct the measure-theoretic concept of a product measure (restricting to the case of probability measures to avoid unnecessary technicalities), and use this to set up the probabilistic notion of independence on a rigorous footing. (To quote Durrett: “measure theory ends and probability theory begins with the definition of independence.”) We will be able to take virtually any collection of random variables (or probability distributions) and couple them together to be independent via the product measure construction, though for infinite products there is the slight technicality (a requirement of the Kolmogorov extension theorem) that the random variables need to range in standard Borel spaces. This is not the only way to couple together such random variables, but it is the simplest and the easiest to compute with in practice, as we shall see in the next few sets of notes.
— 1. Product measures —
It is intuitively obvious that Lebesgue measure on
ought to be related to Lebesgue measure
on
by the relationship
for any Borel sets . This is in fact true (see Exercise 5 below), and is part of a more general phenomenon, which we phrase here in the case of probability measures:
Theorem 1 (Product of two probability spaces) Let
and
be probability spaces. Then there is a unique probability measure
on
with the property that
for all
. Furthermore, we have the following two facts:
- (Tonelli theorem) If
is measurable, then for each
, the function
is measurable on
, and the function
is measurable on
. Similarly, for each
, the function
is measurable on
and
is measurable on
. Finally, we have
- (Fubini theorem) If
is absolutely integrable, then for
-almost every
, the function
is absolutely integrable on
, and the function
is absolutely integrable on
. Similarly, for
-almost every
, the function
is absolutely integrable on
and
is absolutely integrable on
. Finally, we have
The Fubini and Tonelli theorems are often used together (so much so that one may refer to them as a single theorem, the Fubini-Tonelli theorem, often also just referred to as Fubini’s theorem in the literature). For instance, given an absolutely integrable function and an absolutely integrable function
, the Tonelli theorem tells us that the tensor product
defined by
for , is absolutely integrable and one has the factorisation
Our proof of Theorem 1 will be based on the monotone class lemma that allows one to conveniently generate a -algebra from a Boolean algebra. (In Durrett, the closely related
theorem is used in place of the monotone class lemma.) Define a monotone class in a set
to be a collection
of subsets of
with the following two closure properties:
- If
are a countable increasing sequence of sets in
, then
.
- If
are a countable decreasing sequence of sets in
, then
.
Thus for instance any -algebra is a monotone class, but not conversely. Nevertheless, there is a key way in which monotone classes “behave like”
-algebras:
Lemma 2 (Monotone class lemma) Let
be a Boolean algebra on
. Then
is the smallest monotone class that contains
.
Proof: Let be the intersection of all the monotone classes that contain
. Since
is clearly one such class,
is a subset of
. Our task is then to show that
contains
.
It is also clear that is a monotone class that contains
. By replacing all the elements of
with their complements, we see that
is necessarily closed under complements.
For any , consider the set
of all sets
such that
,
,
, and
all lie in
. It is clear that
contains
; since
is a monotone class, we see that
is also. By definition of
, we conclude that
for all
.
Next, let be the set of all
such that
,
,
, and
all lie in
for all
. By the previous discussion, we see that
contains
. One also easily verifies that
is a monotone class. By definition of
, we conclude that
. Since
is also closed under complements, this implies that
is closed with respect to finite unions. Since this class also contains
, which contains
, we conclude that
is a Boolean algebra. Since
is also closed under increasing countable unions, we conclude that it is closed under arbitrary countable unions, and is thus a
-algebra. As it contains
, it must also contain
.
We now begin the proof of Theorem 1. We begin with the uniqueness claim. Suppose that we have two measures on
that are product measures of
and
in the sense that
for all and
. If we then set
to be the collection of all
such that
, then
contains all sets of the form
with
and
. In fact
contains the collection
of all sets that are “elementary” in the sense that they are of the form
for finite
and
for
, since such sets can be easily decomposed into a finite union of disjoint products
, at which point the claim follows from (4) and finite additivity. But
is a Boolean algebra that generates
as a
-algebra, and from continuity from above and below we see that
is a monotone class. By the monotone class lemma, we conclude that
is all of
, and hence
. This gives uniqueness. Now we prove existence. We first claim that for any measurable set
, the sets
are measurable in
. Indeed, the claim is obvious for sets
that are “elementary” in the sense that they belong to the Boolean algebra
defined previously, and the collection of all such sets is a monotone class, so the claim follows from the monotone class lemma. A similar argument (relying on monotone or dominated convergence) shows that the function
is measurable in for all
. Thus, for any
, we can define the quantity
by
A routine application of the monotone convergence theorem verifies that is a countably additive measure; one easily checks that (2) holds for all
, and in particular
is a probability measure.
By construction, we see that the identity
holds (with all functions integrated being measurable) whenever is an indicator function
with
. By linearity of integration, the same identity holds (again with all functions measurable) when
is an unsigned simple function. Since any unsigned measurable function
can be expressed as the monotone non-decreasing limit of unsigned simple functions
(for instance, one can round
down to the largest multiple of
that is less than
and
), the above identity also holds for unsigned measurable
by the monotone convergence theorem. Applying this fact to the absolute value
of an absolutely integrable function
, we conclude for such functions that
which by Markov’s inequality implies that
for -almost every
. In other words, the function
is absolutely integrable on
for
-almost every
. By monotonicity we conclude that
and hence the function is absolutely integrable. Hence it makes sense to ask whether the identity
holds for absolutely integrable , as both sides are well-defined. We have already established this claim when
is unsigned and absolutely integrable; by subtraction this implies the claim for real-valued absolutely integrable
, and by taking real and imaginary parts we obtain the claim for complex-valued absolutely integrable
.
We may reverse the roles of and
, and define
instead by the formula
By the previously proved uniqueness of product measure, we see that this defines the same product measure as previously. Repeating the previous arguments we obtain all the above claims with the roles of
and
reversed. This gives all the claims required for Theorem 1.
One can extend the product construction easily to finite products:
Exercise 3 (Finite products) Show that for any finite collection
of probability spaces, there exists a unique probability measure
on
such that
whenever
for
. Furthermore, show that
for any partition
(after making the obvious identification between
and
). Thus for instance one has the associativity property
for any probability spaces
for
.
Exercise 4 Let
be probability measures on
, and let
be their Stieltjes measure functions. Show that
is the unique probability measure
on
whose Stietljes measure function
is the tensor product
of
.
By writing as products of pairs of probability spaces in many different ways, one can obtain a higher-dimensional analogue of the Fubini and Tonelli theorems; we leave the precise statement of such a theorem to the interested reader.
It is important to be aware that the Fubini theorem identity
for measurable functions that are not unsigned, are usually only justified when
is absolutely integrable on
, or equivalently (by the Tonelli theorem) the function
is absolutely integrable on
(or that
is absolutely integrable on
. Without this joint absolute integrability (and without any unsigned property on
), the identity (5) can fail even if both sides are well-defined. For instance, let
be the unit interval
, and let
be the uniform probability measure on this interval, and set
One can check that both sides of (5) are well-defined, but that the left-hand side is and the right-hand side is
. Of course, this function is neither unsigned nor jointly absolutely integrable, so this counterexample does not violate either of the Fubini or Tonelli theorems. Thus one should take care to only interchange integrals when the integrands are known to be either unsigned or jointly absolutely integrable, or if one has another way to rigorously justify the exchange of integrals.
The above theory extends from probability spaces to finite measure spaces, and more generally to measure spaces that are -finite, that is to say they are expressable as the countable union of sets of finite measure. (With a bit of care, some portions of product measure theory are even extendible to non-sigma-finite settings, though I urge caution in applying these results blindly in that case.) We will not give the details of these generalisations here, but content ourselves with one example:
Exercise 5 Establish (1) for all Borel sets
. (Hint:
can be viewed as the disjoint union of a countable sequence of sets of measure
.)
Remark 6 When doing real analysis (as opposed to probability), it is convenient to complete the Borel
-algebra
on spaces such as
, to form the larger Lebesgue
-algebra
, defined as the collection of all subsets
in
that differ from a Borel set
in
by a sub-null set, in the sense that
for some Borel subset
of
of zero Lebesgue measure. There are analogues of the Fubini and Tonelli theorems for such complete
-algebras; see this previous lecture notes for details. However one should be cautioned that the product
of Lebesgue
-algebras is not the Lebesgue
-algebra
, but is instead an intermediate
-algebra between
and
, which causes some additional small complications. For instance, if
is Lebesgue measurable, then the functions
can only be found to be Lebesgue measurable on
for almost every
, rather than for all
. We will not dwell on these subtleties further here, as we will rarely have any need to complete the
-algebras used in probability theory.
It is also important in probability theory applications to form the product of an infinite number of probability spaces for
, where
can be infinite or even uncountable. Recall from Notes 0 that the product
-algebra
on
is defined to be the
-algebra generated by the sets
for
and
, where
is the usual coordinate projection. Equivalently, if we define an elementary set to be a subset of
of the form
, where
is a finite subset of
,
is the obvious projection map to
, and
is a measurable set in
, then
can be defined as the
-algebra generated by the collection
of elementary sets. (Elementary sets are the measure-theoretic analogue of cylinder sets in point set topology.) For future reference we note the useful fact that
is a Boolean algebra.
We define a product measure to be a probability measure on the measurable space
which extends all of the finite products in the sense that
for all finite subsets of
and all
in
, where
. If this product measure exists, it is unique:
Exercise 7 Show that for any collection of probability spaces
for
, there is at most one product measure
. (Hint: adapt the uniqueness argument in Theorem 1 that used the monotone class lemma.)
In the case of finite , the finite product constructed in Exercise 3 is clearly the unique product. But for infinite
, the construction of product measure is a more nontrivial issue. We can generalise the problem as follows:
Problem 8 (Extension problem) Let
be a collection of measurable spaces. For each finite
, let
be a probability measure on
obeying the compatibility condition
for all finite
and
, where
is the obvious restriction. Can one then define a probability measure
on
such that
for all finite
and
?
Note that the compatibility condition (6) is clearly necessary if one is to find a measure obeying (7).
Again, one has uniqueness:
Exercise 9 Show that for any
and
for finite
as in the above extension problem, there is at most one probability measure
with the stated properties.
The extension problem is trivial for finite , but for infinite
there are unfortunately examples where the probability measure
fails to exist. However, there is one key case in which we can build the extension, thanks to the Kolmogorov extension theorem. Call a measurable space
standard Borel if it is isomorphic as a measurable space to a Borel subset of the unit interval
with Borel measure, that is to say there is a bijection
from
to a Borel subset
of
such that
and
are both measurable. (In Durrett, such spaces are called nice spaces.) Note that one can easily replace
by other standard spaces such as
if desired, since these spaces are isomorphic as measurable spaces (why?).
Theorem 10 (Kolmogorov extension theorem) Let the situation be as in Problem 8. If all the measurable spaces
are standard Borel, then there exists probability measure
solving the extension problem (which is then unique, thanks to Exercise 9).
The proof of this theorem is lengthy and is deferred to the next (optional) section. Specialising to the product case, we conclude
Corollary 11 Let
be a collection of probability spaces with
standard Borel. Then there exists a product measure
(which is then unique, thanks to Exercise 7).
Of course, to use this theorem we would like to have a large supply of standard Borel spaces. Here is one tool that often suffices:
Lemma 12 Let
be a complete separable metric space, and let
be a Borel subset of
. Then
(with the Borel
-algebra) is standard Borel.
Proof: Let us call two topological spaces Borel isomorphic if their corresponding Borel structures are isomorphic as measurable spaces. Using the binary expansion, we see that is Borel isomorphic to
(the countable number of points that have two binary expansions can be easily permuted to obtain a genuine isomorphism). Similarly
is Borel isomorphic to
. Since
is in bijection with
, we conclude that
is Borel isomorphic to
. Thus it will suffice to to show that every complete separable metric space
is Borel isomorphic to a Borel subset of
. But if we let
be a countable dense subset in
, the map
can easily be seen to be a Borel isomorphism between and a Borel subset of
(note the image is the closure of the points
in the uniform norm). The claim follows.
Exercise 13 (Kolmogorov extension theorem, alternate form) For each natural number
, let
be a probability measure on
with the property that
for
and any box
in
, where we identify
with
in the usual manner. Show that there exists a unique probability measure
on
(with the product
-algebra, or equivalently the Borel
-algebra on the product topology) such that
for all
and Borel sets
.
— 2. Proof of the Kolmogorov extension theorem (optional) —
We now prove Theorem 10. By the definition of a standard Borel space, we may assume without loss of generality that each is a Borel subset of
with the Borel
-algebra, and then by extending each
to
we may in fact assume without loss of generality that each
is simply
with the Borel
-algebra. Thus each
for finite
is a probability measure on the cube
.
We will exploit the regularity properties of such measures:
Exercise 14 Let
be a finite set, and let
be a probability measure on
(with the Borel
-algebra). For any Borel set
in
, establish the inner regularity property
and the outer regularity property
Hint: use the monotone class lemma.
Another way of stating the above exercise is that finite Borel measures on the cube are automatically Radon measures. In fact there is nothing particularly special about the unit cube here; the claim holds for any compact separable metric spaces. Radon measures are often used in real analysis (see e.g. these lecture notes) but we will not develop their theory further here.
Observe that one can define the elementary measure of any elementary set
in
by defining
for any finite and any Borel
. This definition is well-defined thanks to the compatibility hypothesis (6). From the finite additivity of the
it is easy to see that
is a finitely additive probability measure on the Boolean algebra
of elementary sets.
We would like to extend to a countably additive probability measure on
. The standard approach to do this is via the Carathéodory extension theorem in measure theory (or the closely related Hahn-Kolmogorov theorem); this approach is presented in these previous lecture notes, and a similar approach is taken in Durrett. Here, we will try to avoid developing the Carathéodory extension theorem, and instead take a more direct approach similar to the direct construction of Lebesgue measure, given for instance in these previous lecture notes.
Given any subset (not necessarily Borel), we define its outer measure
to be the quantity
where we say that is an open elementary cover of
if each
is an open elementary set, and
. Some properties of this outer measure are easily established:
Exercise 15
- (i) Show that
.
- (ii) (Monotonicity) Show that if
then
.
- (iii) (Countable subadditivity) For any countable sequence
of subsets of
, show that
. In particular (from part (i)) we have the finite subadditivity
for all
.
- (iv) (Elementary sets) If
is an elementary set, show that
. (Hint: first establish the claim when the elementary set
is also compact , relying heavily on the regularity properties of the
provided by Exercise 14, then extend to the general case by further heavy reliance on regularity.) In particular, we have
.
- (v) (Approximation) Show that if
, then for any
there exists an elementary set
such that
. (Hint: use the monotone class lemma. When dealing with an increasing sequence of measurable sets
obeying the required property, approximate these sets by an increasing sequence of elementary sets
, and use the finite additivity of elementary measure and the fact that bounded monotone sequences converge.)
From part (v) of the above exercise, we see that every can be viewed as a “limit” of a sequence
of elementary sets such that
. From parts (iii), (iv) we see that the sequence
is a Cauchy sequence and thus converges to a limit, which we denote
; one can check from further application of (iii), (iv) that this quantity does not depend on the specific choice of
. (Indeed, from subadditivity we see that
.) From definition we see that
extends
(thus
for any elementary set
), and from the above exercise one checks that
is countably additive. Thus
is a probability measure with the desired properties, and the proof of the Kolmogorov extension theorem is complete.
— 3. Independence —
Using the notion of product measure, we can now quickly define the notion of independence:
Definition 16 A collection
of random variables
(each of which take values in some measurable space
) is said to be jointly independent, if the distribution of
is the product of the distributions of the
. Or equivalently (after expanding all the definitions), we have
for all finite
and all measurable subsets
of
. We say that two random variables
are independent (or that
is independent of
) if the pair
is jointly independent.
It is worth reiterating that unless otherwise specified, all random variables under consideration are being modeled by a single probability space. The notion of independence between random variables does not make sense if the random variables are only being modeled by separate probability spaces; they have to be coupled together into a single probability space before independence becomes a meaningful notion.
Independence is a non-trivial notion only when one has two or more random variables; by chasing through the definitions we see that any collection of zero or one variables is automatically jointly independent.
Example 17 If we let
be drawn uniformly from a product
of two Borel sets
in
of positive finite Lebesgue measure, then
and
are independent. However, if
is drawn from uniformly from another shape (e.g. a parallelogram), then one usually does not expect to have independence.
As a special case of the above definition, a finite family of random variables taking values in
is jointly independent if one has
for all measurable in
for
.
Suppose that is a family of independent random variables, with each
taking values in
. From Exercise 3 we see that
whenever are disjoint finite subsets of
,
is the tuple
, and
is a measurable subset of
. In particular, we see that the tuples
are also jointly independent. This implies in turn that
are jointly independent for any measurable functions
. Thus, for instance, if
are jointly independent random variables taking values in
respectively, then
and
are independent for any measurable
and
. In particular, if two scalar random variables
are jointly independent of a third random variable
(i.e. the triple
are jointly independent), then combinations such as
or
are also independent of
.
We remark that there is a quantitative version of the above facts used in information theory, known as the data processing inequality, but this is beyond the scope of this course.
If and
are independent scalar random variables, then from the Fubini and Tonelli theorems we see that
if and
are either both unsigned, or both absolutely integrable. We caution however that the converse is not true: just because two random variables
happen to obey (8) does not necessarily mean that they are independent; instead, we say merely that they are uncorrelated, which is a weaker statement.
More generally, if and
are random variables taking values in ranges
respectively, then
for any scalar functions on
respectively, provided that
and
are either both unsigned, or both absolutely integrable. This is the property of
and
which is equivalent to independence (as can be seen by specialising to those
that take values in
): thus for instance independence of two unsigned random variables
entails not only (8), but
,
, etc.. Similarly when discussing the joint independence of larger numbers of random variables. It is this ability to easily decouple expectations of independent random variables that make independent variables particularly easy to compute with in probability.
Exercise 18 Show that a random variable
taking values in a locally compact,
-compact metric space is independent of itself (i.e.
and
are independent) if and only if
is almost surely equal to a constant.
Exercise 19 Show that a constant (deterministic) random variable is independent of any other random variable.
Exercise 20 Let
be discrete random variables (i.e. they take values in at most countable spaces
equipped with the discrete sigma-algebra). Show that
are jointly independent if and only if one has
for all
.
Exercise 21 Let
be real scalar random variables. Show that
are jointly independent if and only if one has
for all
.
The following exercise demonstrates that probabilistic independence is analogous to linear independence:
Exercise 22 Let
be a finite-dimensional vector space over a finite field
, and let
be a random variable drawn uniformly at random from
. Let
be a non-degenerate bilinear form on
, and let
be non-zero vectors in
. Show that the random variables
are jointly independent if and only if the vectors
are linearly independent.
Exercise 23 Give an example of three random variables
which are pairwise independent (that is, any two of
are independent of each other), but not jointly independent. (Hint: one can use the preceding exercise.)
Another analogy is with orthogonality:
Exercise 24 Let
be a random variable taking values in
with the Gaussian distribution, in the sense that
(where
denotes the Euclidean norm on
), and let
be vectors in
. Show that the random variables
(with
denoting the Euclidean inner product) are jointly independent if and only if the
are pairwise orthogonal.
We say that a family of events are jointly independent if their indicator random variables
are jointly independent. Undoing the definitions, this is equivalent to requiring that
for all disjoint finite subsets of
. This condition is complicated, but simplifies in the case of just two events:
Exercise 25
- (i) Show that two events
are independent if and only if
.
- (ii) If
are events, show that the condition
is necessary, but not sufficient, to ensure that
are jointly independent.
- (iii) Given an example of three events
that are pairwise independent, but not jointly independent.
Because of the product measure construction, it is easy to insert independent sources of randomness into an existing randomness model by extending that model, thus giving a more useful version of Corollaries 27 and 31 of Notes 0:
Proposition 26 Suppose one has a collection of events and random variables modeled by some probability space
, and let
be a probability measure on a measurable space
. Then there exists an extension
of the probability space
, and a random variable
modeled by
taking values in
, such that
has distribution
and is independent of all random variables that were previously modeled by
.
More generally, given a finite collectionof probability measures on measurable spaces
, there exists an extension
of
and random variables
modeled by
taking values in
for each
, such that each
has distribution
and
and
are jointly independent for any random variable
that was previously modeled by
.
If theare all standard Borel spaces, then one can also take
to be infinite (even if
is uncountable).
Proof: For the first part, we define the extension to be the product of
with the probability space
, with factor map
defined by
, and with
modeled by
. It is then routine to verify all the claimed properties. The other parts of the proposition are proven similarly, using Proposition 11 for the final part.
Using this proposition, for instance, one can start with a given random variable and create an independent copy
of that variable, which has the same distribution as
but is independent of
, by extending the probability model. Indeed one can create any finite number of independent copies, or even an infinite number of
takes values in a standard Borel space (in particular, one can do this if
is a scalar random variable). A finite or infinite sequence
of random variables that are jointly independent and all have the same distribution is said to be an independent and identically distributed (or iid for short) sequence of random variables. The above proposition allows us to easily generate such sequences by extending the sample space as necessary.
Exercise 27 Let
be random variables that are independent and identically distributed copies of the Bernoulli random variable with expectation
, that is to say the
are jointly independent with
for all
.
- (i) Show that the random variable
is uniformly distributed on the unit interval
.
- (ii) Show that the random variable
has the distribution of Cantor measure (constructed for instance in Example 1.2.4 of Durrett).
Note that part (i) of this exercise provides a means to construct Lebesgue measure on the unit interval (although, when one unpacks the construction, it is actually not too different from the standard construction, as given for instance in this previous set of notes).
Given two square integrable real random variables , the covariance
between the two is defined by the formula
The covariance is well-defined thanks to the Cauchy-Schwarz inequality, and it is not difficult to see that one has the alternate formula
for the covariance. Note that the variance is a special case of the covariance: .
From construction we see that if are independent square integrable variables, then the covariance
vanishes. The converse is not true:
Exercise 28 Give an example of two square-integrable real random variables
which have vanishing covariance
, but are not independent.
However, there is one key case in which the converse does hold, namely that of gaussian random vectors.
Exercise 29 A random vector
taking values in
is said to be a gaussian random vector if there exists
and an
positive definite real symmetric matrix
such that
for all Borel sets
(where we identify elements of
with column vectors). The distribution of
is called a multivariate normal distribution.
- (i) If
is a gaussian random vector with the indicated parameters
, show that
and
for
. In particular
. Thus we see that the parameters of a gaussian random variable can be recovered from the mean and covariances.
- (ii) If
is a gaussian random vector and
, show that
and
are independent if and only if the covariance
vanishes. Furthermore, show that
are jointly independent if and only if all the covariances
for
vanish. In particular, for gaussian random vectors, joint independence is equivalent to pairwise independence. (Contrast this with Exercise 23.)
- (iii) Give an example of two real random variables
, each of which is gaussian, and for which
, but such that
and
are not independent. (Hint: take
to be the product of
with a random sign.) Why does this not contradict (ii)?
We have discussed independence of random variables, and independence of events. It is also possible to define a notion of independence of -algebras. More precisely, define a
-algebra of events to be a collection
of events that contains the empty event, is closed under Boolean operations (in particular, under complements
) and under countable conjunctions and countable disjunctions. Each such
-algebra, when using a probability space model
, is modeled by a
-algebra
of measurable sets in
, which behaves under an extension
in the obvious pullback fashion:
A random variable taking values in some range
is said to be measurable with respect to a
-algebra of events
if the event
lies in
for every measurable subset
of
; in terms of a probabilistic model
,
is measurable with respect to
if and only if
is measurable with respect to
. Note that every random variable
generates a
-algebra
of events, defined to be the collection of all events of the form
for
a measurable subset of
; this is the smallest
-algebra with respect to which
is measurable. More generally, any collection
of random variables, one can define the
-algebra
to be the smallest
-algebra of events with respect to which all of the
are measurable; in terms of a model
, we have
where is the range of
. Similarly, any collection
of events generates a
-algebra of events
, defined as the smallest
-algebra of events that contains all of the
; with respect to a model
, one has
Definition 30 A collection
of
-algebras of events are said to be jointly independent if, whenever
is a random variable measurable with respect to
for
, the tuple
is jointly independent. Equivalently,
is jointly independent if and only if one has
whenever
is a finite subset of
and
for
(why is this equivalent?).
Thus, for instance, and
are independent
-algebras of events if and only if one has
for all and
, that is to say that all the events in
are independent of all the events in
.
The above notion generalises the notion of independence for random variables:
Exercise 31 If
are a collection of random variables, show that
are jointly independent random variables if and only if
are jointly independent
-algebras.
Exercise 32 Let
be a sequence of random variables. Show that
are jointly independent if and only if
is independent of
for all natural numbers
.
Suppose one has a sequence of random variables (such a sequence can be referred to as a discrete stochastic process). For each natural number
, we can define the
-algebras
, as the smallest
algebra that makes all of the
for
measurable; for instance, this
-algebra contains any event that is definable in terms of measurable relations of finitely many of the
, together with countable boolean operations on such events. These
-algebras are clearly decreasing in
. We can define the tail
-algebra
to be the intersection of all these
-algebras, that is to say
consists of those events which lie in
for every
. For instance, if the
are scalar random variables that converge almost surely to a limit
, then we see that (after modification on a null set)
is measurable with respect to the tail
-algebra
.
We have the remarkable Kolmogorov 0-1 law that says that the tail -algebra of a sequence of independent random variables is essentially trivial:
Theorem 33 (Kolmogorov zero-one law) Let
be a sequence of jointly independent random variables. Then every event
in the tail
-algebra
has probability equal to either
or
.
As a corollary of the zero-one law, note that any real scalar tail random variable will be almost surely constant (because, for each rational
, the event
is either almost surely true or almost surely false). Similarly for tail random variables taking values in
or
.
Example 34 Let
be a sequence of jointly independent random variables in
(not necessarily identically distributed). The random variable
is measurable in the tail algebra, and hence must be almost surely constant, thus there exists
such that
almost surely. Similarly there exists
such that
. Thus, either we have
and the
converge almost surely to a deterministic limit, or
and the
almost surely do not converge. What cannot happen is (for instance) that
converges with probability
, and diverges with probability
; the zero-one law forces the only available probabilities of tail events to be zero or one.
Proof: Since are jointly independent, the
-algebra
is independent of
for any
. In particular,
is independent of
. Since the
-algebra
is generated by the
for
, a simple application of the monotone class lemma then shows that
is also independent of
. But
contains
, hence
is independent of itself. But the only events
that are independent of themselves have probability
or
, and the claim follows.
Note that the zero-one law gives no guidance as to which of the two probabilities actually occurs for a given tail event. This usually cannot be determined from such “soft” tools as the zero-one law; instead one often has to work with more “hard” estimates, in particular in explicit inequalities for the probabilities of various events that approximate the given tail event. On the other hand, the proof technique used to prove the Kolmogorov zero-one law is quite general, and is often adapted to prove other zero-one laws in the probability literature.
The zero-one law suggests that many asymptotic statistics of random variables will almost surely have deterministic values. We will see specific examples of this in the next few notes, when we discuss the law of large numbers and the central limit theorem.

142 comments
Comments feed for this article
28 September, 2023 at 1:06 am
Han Bing
Also, may I ask why is the compatibility condition (6) in the extension problem necessary if one is to find a measure obeying (7)?
obeying (7)?
[(7) follows from two applications of (6) since . -T.]
. -T.]
28 September, 2023 at 1:37 am
Han Bing
Finally, I have a question regarding the definition of product measure following Remark 5: , for it seems that the set
, for it seems that the set  in
in  is not unique.
is not unique.
The pre-image is uniquely determined by
is uniquely determined by 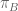 and
and  . -T.]
. -T.]
29 September, 2023 at 4:08 pm
Han Bing
Thank you Prof Tao, see it now.
30 September, 2023 at 6:50 pm
Anonymous
Dear Prof Tao: of sets on which $\mu_A$ and $\mu’_A$ agree is a monotone class containing the elementary sets, and hence is the entire
of sets on which $\mu_A$ and $\mu’_A$ agree is a monotone class containing the elementary sets, and hence is the entire  by the monotone class lemma. But then where is the compatibility condition on
by the monotone class lemma. But then where is the compatibility condition on  used?
used?
What differs the solution of Exercise 9 to that of Exercise 7? It seems that in both cases one directly show that the collection
30 September, 2023 at 6:59 pm
Terence Tao
The compatibility condition is not, strictly speaking, needed for the uniqueness aspect for Problem 8, but it is needed for existence.
30 September, 2023 at 10:02 pm
Han Bing
So we can use the same argument for both Exercise 7 and Exercise 9?
4 October, 2023 at 2:55 pm
Han Bing
Dear prof Tao: is measurable?
is measurable?
In the proof of Lemma 12, how do we show that the map
4 October, 2023 at 3:32 pm
Han Bing
And do we assume the fact that the binary expansion of points in![[0, 1]](https://s0.wp.com/latex.php?latex=%5B0%2C+1%5D&bg=ffffff&fg=545454&s=0&c=20201002) is essentially unique to be known?
is essentially unique to be known?
5 October, 2023 at 11:04 am
Terence Tao
Yes, broadly speaking I would permit anything covered in a standard undergraduate mathematics curriculum to be applied to these sorts of arguments.
5 October, 2023 at 11:03 am
Terence Tao
One can first show that each individual function $x \mapsto \frac{d(x,q_i)}{1+d(x,q_i)}$ is measurable.
6 October, 2023 at 3:52 pm
Han Bing
Thank you professor.
6 October, 2023 at 4:45 pm
Han Bing
Dear professor Tao: should be
should be  . And do we expect to do this Exercise after reading the next section on the proof of the original extension theorem?
. And do we expect to do this Exercise after reading the next section on the proof of the original extension theorem?
In the second display of Exercise 13 (the alternate Kolmogorov extension),
[Corrected, thanks. One can establish Exercise 13 using the Kolmogorov Extension Theorem (Theorem 10) as a “black box”; reading the proof may provide additional intuition but is not, strictly speaking, necessary. -T]
11 October, 2023 at 5:11 pm
Han Bing
Thank you professor. Following your hint, one first show that obeys the compatibility condition of Theorem 10 by showing that
obeys the compatibility condition of Theorem 10 by showing that  for any box
for any box  in
in  and any
and any  , is this what you mean by “black box”?
, is this what you mean by “black box”?
[Yes – T.]
16 October, 2023 at 3:05 am
Anonymous
Dear professor Tao: be the collection of Borel sets in the unit cube that can be approximated from inside by compact
be the collection of Borel sets in the unit cube that can be approximated from inside by compact 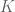 and from outside by open
and from outside by open  such that
such that  , then we want $latex $ to be the Borel
, then we want $latex $ to be the Borel  -algebra of the cube, can you give some further hint on how the monotone class lemma is being used to obtain this conclusion?
-algebra of the cube, can you give some further hint on how the monotone class lemma is being used to obtain this conclusion?
For Exercise 14, if we let
21 October, 2023 at 3:22 am
Anonymous
Hello professor Tao: Regarding the hint on part 4 of Exercise 15, I struggle to justify the fact that compact sets are elementary, given a compact![K \subset [0,1]^A](https://s0.wp.com/latex.php?latex=K+%5Csubset+%5B0%2C1%5D%5EA&bg=ffffff&fg=545454&s=0&c=20201002) , how can we express it as
, how can we express it as  ?
?
[Not all compact sets are elementary; but the intention of the hint is to first work with sets that are both compact and elementary. I will reword the hint to reduce confusion. -T]
26 October, 2023 at 5:59 pm
Anonymous
Thank you for clarification professor Tao. Can you provide some further hint on how to establish the claim for elementary sets? If is compact, then so is
is compact, then so is  , but I struggled to see how this helps.
, but I struggled to see how this helps.
30 October, 2023 at 2:28 am
Anonymous
After one shows the result for compact elementary sets, then one generalizes to all elementary sets by showing that outer measure is inner regular on elementary sets. May I ask if this is what the hint is suggesting?
1 November, 2023 at 4:57 pm
Terence Tao
That is what the second part of the hint is indicating. For the first part, you may find some of the techniques in https://terrytao.wordpress.com/2010/10/21/245a-problem-solving-strategies/ to be helpful.
3 November, 2023 at 4:33 am
Anonymous
Thank you so much for clarification, dear prof Tao. For any elementary set![E \subset [0,1]^A](https://s0.wp.com/latex.php?latex=E+%5Csubset+%5B0%2C1%5D%5EA&bg=ffffff&fg=545454&s=0&c=20201002) , we show that
, we show that  by noting that LHS
by noting that LHS 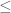 RHS by definition of outer measure, and LHS
RHS by definition of outer measure, and LHS 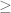 RHS by outer regularity of
RHS by outer regularity of  . From this can’t one derive the result for all elementary
. From this can’t one derive the result for all elementary  rather than
rather than  compact elementary?
compact elementary?
9 November, 2023 at 4:36 am
Anonymous
Dear professor Tao: be the collection of Borel sets of
be the collection of Borel sets of ![[0,1]^B](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5EB&bg=ffffff&fg=545454&s=0&c=20201002) on which $\mu_B$ is regular, can’t we show that
on which $\mu_B$ is regular, can’t we show that  is a
is a  -algebra and thus
-algebra and thus ![G = \mathcal{B}[[0,1]^B]](https://s0.wp.com/latex.php?latex=G+%3D+%5Cmathcal%7BB%7D%5B%5B0%2C1%5D%5EB%5D&bg=ffffff&fg=545454&s=0&c=20201002) ? Why is the monotone class lemma necessary for the solution?
? Why is the monotone class lemma necessary for the solution?
For Exercise 14 if one let
[Perhaps this can be done directly, but I don’t think it is completely obvious to show that is a
is a  -algebra just from the definitions. -T]
-algebra just from the definitions. -T]
9 November, 2023 at 11:27 pm
Anonymous
Set![\displaystyle G = \{E \in \mathcal{B}[[0,1]^B]: \forall \varepsilon > 0, \exists K \subset E \subset U\ \text{with}\ \mu_B(U \setminus K) < \varepsilon\}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+G+%3D+%5C%7BE+%5Cin+%5Cmathcal%7BB%7D%5B%5B0%2C1%5D%5EB%5D%3A+%5Cforall+%5Cvarepsilon+%3E+0%2C+%5Cexists+K+%5Csubset+E+%5Csubset+U%5C+%5Ctext%7Bwith%7D%5C+%5Cmu_B%28U+%5Csetminus+K%29+%3C+%5Cvarepsilon%5C%7D&bg=ffffff&fg=545454&s=0&c=20201002) ,
, 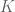 compact and
compact and  open. We can verify that
open. We can verify that  is a Boolean algebra. Let
is a Boolean algebra. Let  , with
, with  be such that
be such that  for all
for all  , we see that
, we see that  . From this and continuity from below we obtain
. From this and continuity from below we obtain  such that
such that  ,
,  with
with  ,
,  compact and
compact and  open. That is,
open. That is,  . Hence
. Hence  is a
is a  -algebra. Note that
-algebra. Note that  contains all open sets
contains all open sets  . For if
. For if ![U \subset [0,1]^B](https://s0.wp.com/latex.php?latex=U+%5Csubset+%5B0%2C1%5D%5EB&bg=ffffff&fg=545454&s=0&c=20201002) is open, then clearly it can be approximated from above by itself. By expressing
is open, then clearly it can be approximated from above by itself. By expressing  as the union of a sequence of closed boxes
as the union of a sequence of closed boxes  , and taking
, and taking  so the sequence is increasing, we see again by continuity from below that
so the sequence is increasing, we see again by continuity from below that  can be approximated from below by compact sets as well. As the Borel
can be approximated from below by compact sets as well. As the Borel  -algebra is generated by the open sets, we get the desired result.
-algebra is generated by the open sets, we get the desired result.
May I ask why the hint prefers the approach by the monotone class lemma? Or is this solution flawed?
25 November, 2023 at 7:58 pm
Anonymous
Dear professor Tao: As for for the last part of Exercise 15, can you provide a bit hint on how to construct the increasing sequence and how the finite additivity of the elementary measure is used to control
and how the finite additivity of the elementary measure is used to control  ?
?
27 November, 2023 at 1:36 pm
Anonymous
I meant to ask how should we construct the approximating sequence and how the hint on the finite additivity of elementary measure is used subsequently.
2 December, 2023 at 5:14 pm
Anonymous
Dear professor Tao: May I ask why do we also need an increasing sequence of elementary sets in the last part of Exercise 15? For an increasing sequence of
in the last part of Exercise 15? For an increasing sequence of  obeying the required property, and
obeying the required property, and  , don’t we have by triangle inequality and the fact that bounded monotone sequences converge, that
, don’t we have by triangle inequality and the fact that bounded monotone sequences converge, that  for large enough
for large enough  ?
?
[This argument works also. -T]
3 December, 2023 at 3:07 pm
Anonymous
Thank you so much professor Tao. Yet I realized to control the term , one needs to establish the superadditivity of $\mu^*$ too, can you provide a bit more explanation on your original hint on using an increasing sequence of
, one needs to establish the superadditivity of $\mu^*$ too, can you provide a bit more explanation on your original hint on using an increasing sequence of  and the finite additivity of elementary measure?
and the finite additivity of elementary measure?
4 December, 2023 at 8:00 am
Terence Tao
If one selects to be elementary increasing with
to be elementary increasing with  , then
, then  is summable (because the bounded monotone sequence
is summable (because the bounded monotone sequence  converges, and from this and countable subadditivity (and the triangle inequality) one can show that
converges, and from this and countable subadditivity (and the triangle inequality) one can show that  goes to zero as
goes to zero as 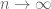 .
.
4 December, 2023 at 2:17 pm
Anonymous
Thank you so much professor Tao!
4 December, 2023 at 8:40 pm
Anonymous
For the approximating sequence , and
, and  , I use the increasing sequence
, I use the increasing sequence  , then the triangle inequality finally gives
, then the triangle inequality finally gives  for some big
for some big  . However I struggled to construct the initial approximating sequence
. However I struggled to construct the initial approximating sequence  to be increasing.
to be increasing.
5 December, 2023 at 12:57 am
Terence Tao
Actually it will be easier (and already enough) to show that it is increasing up to an error that goes to zero quickly as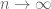 (e.g., up to an error of
(e.g., up to an error of 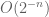 ).
).
6 December, 2023 at 6:14 pm
Anonymous
Dear professor Tao: should be
should be  instead of
instead of  .
.
A minor typo: A redundant word “from” in Example 17. Also, following the second display after Example 17, the domain for the measurable functions
11 December, 2023 at 9:42 am
qshuyu
Dear professor Tao: is drawn uniformly from say a parallelogram?
is drawn uniformly from say a parallelogram?
May I ask why we fail to have independence in Example 17 if
12 December, 2023 at 7:38 am
Terence Tao
If is drawn from a general shape (rather than a rectangle), then in general, knowing the value of
is drawn from a general shape (rather than a rectangle), then in general, knowing the value of  will give some information about
will give some information about 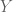 and vice versa. This is for instance the observation that powers Berkson’s paradox.
and vice versa. This is for instance the observation that powers Berkson’s paradox.
11 December, 2023 at 11:57 am
qshuyu
Also, can you elaborate more on your comment above Exercise 18 where you state “This is the property of and
and 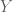 which is equivalent to independence (as can be seen by specialising to those
which is equivalent to independence (as can be seen by specialising to those  that take values in
that take values in 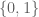 “)?
“)?
12 December, 2023 at 7:40 am
Terence Tao
If for instance and
and  then
then  and
and  .
.
12 December, 2023 at 9:09 am
qshuyu
Thank you so much.
13 December, 2023 at 12:51 am
Anonymous
Dear professor Tao: -compact space is Lindelöf, we can find a point
-compact space is Lindelöf, we can find a point 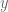 in the range of
in the range of  such that
such that  for arbitrarily small
for arbitrarily small  . Yet I’m not sure how to get from this to ${\bf P}(X = y) = 1$, does this involve the unused condition of local compactness?
. Yet I’m not sure how to get from this to ${\bf P}(X = y) = 1$, does this involve the unused condition of local compactness?
For Exercise 18, by the fact that every
13 December, 2023 at 10:59 am
Anonymous
It seems that once we get this, then continuity from above alone implies that , may I ask if I miss some technical detail regarding the local compactness part of the condition?
, may I ask if I miss some technical detail regarding the local compactness part of the condition?
16 December, 2023 at 8:25 am
Terence Tao
One can probably relax the topological conditions here somewhat (e.g., a common relaxation is to assume one is on a Polish space, rather than a locally compact, sigma-compact space), but for these notes I did not seek the absolutely minimal regularity hypotheses required to make the assertions valid, as these sorts of technicalities are not really the focus of this probability theory course.
15 December, 2023 at 1:25 am
Anonymous
Dear professor Tao:![(-\infty, t_i]](https://s0.wp.com/latex.php?latex=%28-%5Cinfty%2C+t_i%5D&bg=ffffff&fg=545454&s=0&c=20201002) to extend the independence property to the Borel algebra
to extend the independence property to the Borel algebra ![{\mathcal B}[{\bf R}^n]](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+B%7D%5B%7B%5Cbf+R%7D%5En%5D&bg=ffffff&fg=545454&s=0&c=20201002) , but run into issues in showing that this property is closed under complement and countable union, is this a valid approach?
, but run into issues in showing that this property is closed under complement and countable union, is this a valid approach?
Concerning Exercise 21, I was trying to induct on boxes of the form
15 December, 2023 at 1:26 am
Anonymous
I mean boxes of the form![\prod_{i=1}^n (-\infty, t_i]](https://s0.wp.com/latex.php?latex=%5Cprod_%7Bi%3D1%7D%5En+%28-%5Cinfty%2C+t_i%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
16 December, 2023 at 8:38 am
Terence Tao
Try working as an intermediate step with half-open rectangular boxes (which can be expressed as finite boolean combinations of boxes), and then with half-open elementary sets (finite boolean combinations of those boxes).
18 December, 2023 at 12:12 am
Anonymous
Dear professor Tao: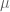 be the law of
be the law of  and
and  the product measure, if
the product measure, if  is the collection of Borel subsets
is the collection of Borel subsets  s.t
s.t  , then
, then  can be shown to be a monotone class. Are you suggesting we show that
can be shown to be a monotone class. Are you suggesting we show that  contains a Boolean algebra containing the half-open elementary sets, and use the monotone class theorem?
contains a Boolean algebra containing the half-open elementary sets, and use the monotone class theorem?
Thank you so much for replying. Let
19 December, 2023 at 10:39 am
Anonymous
Dear professor Tao: should be
should be 
A small typo: In Exercise 22, the random variables
19 December, 2023 at 2:53 pm
Anonymous
(I apologize for my misunderstanding, nothing is wrong here.)
20 December, 2023 at 4:53 pm
Anonymous
Dear professor Tao:
Can you give a bit hint on how linear independence can imply joint independence in Exercise 22?
23 December, 2023 at 5:26 pm
Anonymous
Without loss of generality, set with basis
with basis  , and
, and  . The event
. The event  with
with  corresponds to the system of linear equations
corresponds to the system of linear equations  , where
, where  is the
is the 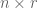 matrix with rows
matrix with rows  , and
, and  . If
. If  is the dimension of the span of
is the dimension of the span of  , then rank(
, then rank( ) is exactly
) is exactly  since it has
since it has  independent rows. Hence the dimension of the solution space equals
independent rows. Hence the dimension of the solution space equals  , and
, and  . Similarly
. Similarly  , so by Exercise 20 the random variables are jointly independent iff the
, so by Exercise 20 the random variables are jointly independent iff the  . i.e. iff the vectors are linearly independent. I don’t see how the non-degeneracy assumption is used here. Is this argument flawed?
. i.e. iff the vectors are linearly independent. I don’t see how the non-degeneracy assumption is used here. Is this argument flawed?
23 December, 2023 at 7:50 pm
Anonymous
I think I see where we need the non-degeneracy assumption. It ensures that we don’t get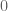 as row vectors of
as row vectors of  (since none of the
(since none of the  ), only then can we safely deduce that
), only then can we safely deduce that  has
has  linearly independent rows. Is this correct, professor Tao?
linearly independent rows. Is this correct, professor Tao?
29 December, 2023 at 11:02 am
Anonymous
Dear professor Tao:
Can you provide a little more directions on Exercise 24(orthogonality and independence)?
[First try the model case where are the standard coordinate bases
are the standard coordinate bases  . You can set
. You can set  if you wish to make things a little more concrete. -T]
if you wish to make things a little more concrete. -T]
2 January, 2024 at 1:09 am
Anonymous
Thank you for replying professor. I find it hard though to use the fact that is a Gaussian random variable. Are we supposed to show this by definition?
is a Gaussian random variable. Are we supposed to show this by definition?
2 January, 2024 at 12:53 pm
Terence Tao
Yes; for instance in the model case , one can compute the distributions of
, one can compute the distributions of  by direct computation (performing one-dimensional Gaussian integrals), and show that the product of these distributions agrees with the distribution of the joint random variable
by direct computation (performing one-dimensional Gaussian integrals), and show that the product of these distributions agrees with the distribution of the joint random variable  .
.
3 January, 2024 at 8:45 am
Anonymous
Let , then
, then  . By direct computation, are you suggesting one show that the integral splits over the intersection if and only if we have orthogonality, professor Tao?
. By direct computation, are you suggesting one show that the integral splits over the intersection if and only if we have orthogonality, professor Tao?
7 January, 2024 at 10:39 pm
Anonymous
Dear professor Tao: For this Exercise is it required to use the rotational invariance of the standard Gaussian distribution, and the linear change of variables formula?
[Yes – T.]
5 January, 2024 at 1:04 am
Anonymous
Dear professor Tao: and
and 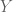 to be independent in the display tagged
to be independent in the display tagged  , because later it is said that “we caution however that the converse is not true…”
, because later it is said that “we caution however that the converse is not true…”
I believe we need the scalar r.v
[Corrected, thanks – T.]
11 January, 2024 at 9:30 pm
Anonymous
Dear professor Tao; should be modeled by
should be modeled by  .
.
In the proof of proposition 26,
22 January, 2024 at 9:34 pm
Anonymous
Dear professor Tao: be the eigenvalue decomposition of
be the eigenvalue decomposition of  , where
, where 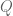 is orthogonal,
is orthogonal,  is diagonal with its
is diagonal with its 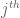 diagonal entry
diagonal entry  the eigenvalue of
the eigenvalue of  corresponding to the
corresponding to the 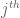 column of
column of 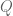 . Then by consecutive linear change of variables, one seems to get
. Then by consecutive linear change of variables, one seems to get  , where
, where  . In particular, the joint distribution splits into product of the marginal distribution of the components, and we get independence automatically, which is obviously incorrect, where did it possibly go wrong?
. In particular, the joint distribution splits into product of the marginal distribution of the components, and we get independence automatically, which is obviously incorrect, where did it possibly go wrong?
I have a conceptual misunderstanding of Exercise 29. Let
23 January, 2024 at 12:37 pm
Anonymous
Dear professor Tao: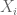 to calculate
to calculate  when the joint pdf does not readily split into product of the marginal pdfs?
when the joint pdf does not readily split into product of the marginal pdfs?
Actually I see the blunder in the derivation now. But may I still ask how should one get the marginal distribution of each component
26 January, 2024 at 11:33 am
Anonymous
Dear professor Tao: is the eigenvalue decomposition of
is the eigenvalue decomposition of  , and
, and  , then
, then  is a copy of
is a copy of  and the fact that
and the fact that  follows by linearity.
follows by linearity.
Regarding Exercise 29, if
This approach gives no information however on the marginal distribution of the components $X_i$, is there a way to calculate the marginal distributions without using the linear transformation theorem for multivariate normal distribution, the proof of which relies in turn on the use of generating functions or characteristic functions, which have not yet been fully developed at this point in the notes?
26 January, 2024 at 8:08 pm
Anonymous
Finally, by change of variables , I have some difficulties showing this evaluate to
, I have some difficulties showing this evaluate to  , can you provide some hint on this, professor Tao?
, can you provide some hint on this, professor Tao?
27 January, 2024 at 11:44 pm
Anonymous
Dear professor Tao: In the second part of Exercise 29, we should have the covariances vanish for all off-diagonal entries rather than just the entries above the diagonal.
30 January, 2024 at 9:10 pm
Anonymous
Dear professor Tao: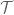 is independent of
is independent of  , may I ask what is the larger class containing the generators
, may I ask what is the larger class containing the generators  to which
to which 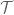 is independent, that allow us to use the said lemma? Why can’t we use induction in this case?
is independent, that allow us to use the said lemma? Why can’t we use induction in this case?
In the proof of the Kolmogorov zero-one law, the monotone class lemma is used to show that
[One applies the monotone class lemma to the collection of events that are independent of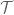 , which is easily seen to be a monotone class containing each of the
, which is easily seen to be a monotone class containing each of the  , and hence
, and hence  . Note that the latter
. Note that the latter  -algebra is not simply the union of the preceding ones, but is instead the
-algebra is not simply the union of the preceding ones, but is instead the  -algebra (or monotone class) generated by that union. -T]
-algebra (or monotone class) generated by that union. -T]