Today I’d like to discuss (in the Tricks Wiki format) a fundamental trick in “soft” analysis, sometimes known as the “limiting argument” or “epsilon regularisation argument”.
Title: Give yourself an epsilon of room.
Quick description: You want to prove some statement about some object
(which could be a number, a point, a function, a set, etc.). To do so, pick a small
, and first prove a weaker statement
(which allows for “losses” which go to zero as
) about some perturbed object
. Then, take limits
. Provided that the dependency and continuity of the weaker conclusion
on
are sufficiently controlled, and
is converging to
in an appropriately strong sense, you will recover the original statement.
One can of course play a similar game when proving a statement about some object
, by first proving a weaker statement
on some approximation
to
for some large parameter N, and then send
at the end.
General discussion: Here are some typical examples of a target statement , and the approximating statements
that would converge to
:
| The event |
The event |
| The statement |
The statement |
Of course, to justify the convergence of to
, it is necessary that
converge to
(or
converge to
, etc.) in a suitably strong sense. (But for the purposes of proving just upper bounds, such as
, one can often get by with quite weak forms of convergence, thanks to tools such as Fatou’s lemma or the weak closure of the unit ball.) Similarly, we need some continuity (or at least semi-continuity) hypotheses on the functions f, g appearing above.
It is also necessary in many cases that the control on the approximating object
is somehow “uniform in
“, although for “
-closed” conclusions, such as measurability, this is not required. [It is important to note that it is only the final conclusion
on
that needs to have this uniformity in
; one is permitted to have some intermediate stages in the derivation of
that depend on
in a non-uniform manner, so long as these non-uniformities cancel out or otherwise disappear at the end of the argument.]
By giving oneself an epsilon of room, one can evade a lot of familiar issues in soft analysis. For instance, by replacing “rough”, “infinite-complexity”, “continuous”, “global”, or otherwise “infinitary” objects with “smooth”, “finite-complexity”, “discrete”, “local”, or otherwise “finitary” approximants
, one can finesse most issues regarding the justification of various formal operations (e.g. exchanging limits, sums, derivatives, and integrals). [It is important to be aware, though, that any quantitative measure on how smooth, discrete, finite, etc.
should be expected to degrade in the limit
, and so one should take extreme caution in using such quantitative measures to derive estimates that are uniform in
.] Similarly, issues such as whether the supremum
of a function on a set is actually attained by some maximiser
become moot if one is willing to settle instead for an almost-maximiser
, e.g. one which comes within an epsilon of that supremum M (or which is larger than
, if M turns out to be infinite). Last, but not least, one can use the epsilon room to avoid degenerate solutions, for instance by perturbing a non-negative function to be strictly positive, perturbing a non-strictly monotone function to be strictly monotone, and so forth.
To summarise: one can view the epsilon regularisation argument as a “loan” in which one borrows an epsilon here and there in order to be able to ignore soft analysis difficulties, and can temporarily be able to utilise estimates which are non-uniform in epsilon, but at the end of the day one needs to “pay back” the loan by establishing a final “hard analysis” estimate which is uniform in epsilon (or whose error terms decay to zero as epsilon goes to zero).
A variant: It may seem that the epsilon regularisation trick is useless if one is already in “hard analysis” situations when all objects are already “finitary”, and all formal computations easily justified. However, there is an important variant of this trick which applies in this case: namely, instead of sending the epsilon parameter to zero, choose epsilon to be a sufficiently small (but not infinitesimally small) quantity, depending on other parameters in the problem, so that one can eventually neglect various error terms and to obtain a useful bound at the end of the day. (For instance, any result proven using the Szemerédi regularity lemma is likely to be of this type.) Since one is not sending epsilon to zero, not every term in the final bound needs to be uniform in epsilon, though for quantitative applications one still would like the dependencies on such parameters to be as favourable as possible.
Prerequisites: Graduate real analysis. (Actually, this isn’t so much a prerequisite as it is a corequisite: the limiting argument plays a central role in many fundamental results in real analysis.) Some examples also require some exposure to PDE.
Example 0. The “soft analysis” components of any real analysis textbook will contain a large number of examples of this trick in action. In particular, any argument which exploits Littlewood’s three principles of real analysis is likely to utilise this trick. Of course, this trick will also occur repeatedly in my 245B lecture notes.
Example 1. (Riemann-Lebesgue lemma) Given any absolutely integrable function , the Fourier transform
is defined by the formula
.
The Riemann-Lebesgue lemma asserts that as
. It is difficult to prove this estimate for f directly, because this function is too “rough”: it is absolutely integrable (which is enough to ensure that
exists and is bounded), but need not be continuous, differentiable, compactly supported, bounded, or otherwise “nice”. But suppose we give ourselves an epsilon of room. Then, as the space
of test functions is dense in
(a fact I will prove later in this course), we can approximate
to any desired accuracy
in the
norm by a smooth, compactly supported function
, thus
. (1)
The point is that is much better behaved than f, and it is not difficult to show the analogue of the Riemann-Lebesgue lemma for
. Indeed, being smooth and compactly supported, we can now justifiably integrate by parts to obtain
for any non-zero , and it is now clear (since
is bounded and compactly supported) that
as
.
Now we need to take limits as . It will be enough to have
converge uniformly to
. But from (1) and the basic estimate
(2)
(which is the single “hard analysis” ingredient in the proof of the lemma) applied to , we see (by the linearity of the Fourier transform) that
and we obtain the desired uniform convergence.
Remark 1. The same argument also shows that is continuous; we leave this as an exercise to the reader.
Remark 2. Example 1 is a model case of a much more general instance of the limiting argument: in order to prove a convergence or continuity theorem for all “rough” functions in a function space, it suffices to first prove convergence or continuity for a dense subclass of “smooth” functions, and combine that with some quantitative estimate in the function space (in this case, (2)) in order to justify the limiting argument.
Example 2. The limiting argument in Example 1 relied on the linearity of the Fourier transform . But, with more effort, it is also possible to extend this type of argument to nonlinear settings. We will sketch (omitting several technical details, which can be found for instance in my PDE book) a very typical instance. Consider a nonlinear PDE, e.g. the nonlinear wave equation
(3)
where is some scalar field, and the t and x subscripts denote differentiation of the field
. Formally – if u is sufficiently smooth, and sufficiently decaying at spatial infinity, one can show that the energy
(4)
is conserved, thus for all t. This can be formally justified by computing the derivative
by differentiating under the integral sign, integrating by parts, and then applying the PDE (3); we leave this as an exercise for the reader. (There are also more fancy ways to see why the energy is conserved, using Hamiltonian or Lagrangian mechanics or by the more general theory of stress-energy tensors, but we will not discuss these here.) However, these justifications do require a fair amount of regularity on the solution u; for instance, requiring u to be three-times continuously differentiable in space and time, and compactly supported in space on each bounded time interval, would be sufficient to make the computations rigorous by applying “off the shelf” theorems about differentiation under the integration sign, etc.
But suppose one only has a much rougher solution, for instance an energy class solution which has finite energy (4), but for which higher derivatives of u need not exist in the classical sense. (There is a non-trivial issue regarding how to make sense of the PDE (3) when u is only in the energy class, since the terms and
do not then make sense classically, but there are standard ways to deal with this, e.g. using weak derivatives, which we will not discuss further here.) Then it is difficult to justify the energy conservation law directly. However, it is still possible to obtain energy conservation by the limiting argument. Namely, one takes the energy class solution u at some initial time (e.g. t=0) and approximates that initial data (the initial position
and initial data
) by a much smoother (and compactly supported) choice
of initial data, which converges back to
in a suitable “energy topology” related to (4) which we will not define here. It then turns out (from the existence theory of the PDE (3)) that one can extend the smooth initial data
to other times t, providing a smooth solution
to that data. For this solution, the energy conservation law
can be justified.
Now we take limits as (keeping t fixed). Since
converges in the energy topology to
, and the energy functional E is continuous in this topology,
converges to
. To conclude the argument, we will also need
to converge to
, which will be possible if
converges in the energy topology to
. Thus in turn follows from a fundamental fact (which requires a certain amount of effort to prove) about the PDE to (4), namely that it is well-posed in the energy class. This means that not only do solutions exist and are unique for initial data in the energy class, but they depend continuously on the initial data in the energy topology; small perturbations in the data lead to small perturbations in the solution, or more formally that the map
from data to solution (say, at some fixed time t) is continuous in the energy topology. This final fact concludes the limiting argument and gives us the desired conservation law
.
Remark 3. It is important that one have a suitable well-posedness theory in order to make the limiting argument work for rough solutions to a PDE; without such a well-posedness theory, it is possible for quantities which are formally conserved to cease being conserved when the solutions become too rough or otherwise “weak”; energy, for instance, could disappear into a singularity and not come back.
Example 3. (Maximum principle) The maximum principle is a fundamental tool in elliptic and parabolic PDE (for example, it is used heavily in the proof of the Poincaré conjecture, see e.g. my lecture notes on this topic). Here is a model example of this principle:
Proposition 1. Let
be a smooth harmonic function on the closed unit disk
. If M is a bound such that
on the boundary
. Then
on the interior as well.
A naive attempt to prove Proposition 1 comes very close to working, and goes like this: suppose for contradiction that the proposition failed, thus u exceeds M somewhere in the interior of the disk. Since u is continuous, and the disk is compact, there must then be a point in the interior of the disk where the maximum is attained. Undergraduate calculus then tells us that
and
are non-positive, which almost contradicts the harmonicity hypothesis
. However, it is still possible that
and
both vanish at
, so we don’t yet get a contradiction.
But we can finish the proof by giving ourselves an epsilon of room. The trick is to work not with the function u directly, but with the modified function , to boost the harmonicity into subharmonicity. Indeed, we have
. The preceding argument now shows that
cannot attain its maximum in the interior of the disk; since it is bounded by
on the boundary of the disk, we we conclude that
is bounded by
on the interior of the disk as well. Sending
we obtain the claim.
Remark 4. Of course, Proposition 1 can also be proven by much more direct means, for instance via the Green’s function for the disk. However, the argument given is extremely robust and applies to a large class of both linear and nonlinear elliptic and parabolic equations, including those with rough variable coefficients.
Exercise 1. Use the maximum modulus principle to prove the Phragmén-Lindelöf principle: if f is complex analytic on the strip , is bounded in magnitude by 1 on the boundary of this strip, and obeys a growth condition
on the interior of the strip, then show that f is bounded in magnitude by 1 throughout the strip. (Hint: multiply f by
for some even integer m.)
Example 4. (Manipulating generalised functions) In PDE one is primarily interested in smooth (classical) solutions; but for a variety of reasons it is useful to also consider rougher solutions. Sometimes, these solutions are so rough that they are no longer functions, but are measures, distributions, or some other concept of “generalised function” or “generalised solution“. For instance, the fundamental solution to a PDE is typically just a distribution or measure, rather than a classical function. A typical example: a (sufficiently smooth) solution to the three-dimensional wave equation with initial position
and initial velocity
is given by the classical formula
where is the unique rotation-invariant probability measure on the sphere
of radius t, or equivalently, the area element dS on that sphere divided by the surface area
of that sphere. (The convolution
of a smooth function
and a (compactly supported) finite measure
is defined by
.)
For this and many other reasons, it is important to manipulate measures and distributions in various ways. For instance, in addition to convolving functions with measures, it is also useful to convolve measures with measures; the convolution of two finite measures on
is defined as the measure which assigns to each measurable set E in
, the measure
. (5)
For sake of concreteness, let’s focus on a specific question, namely to compute (or at least estimate) the measure , where
is the normalised rotation-invariant measure on the unit circle
. It turns out that while
is not absolutely continuous with respect to Lebesgue measure
, the convolution is:
for some absolutely integrable function f on
. But what is this function f? It certainly is possible to compute it from the definition (5), or by other methods (e.g. the Fourier transform), but I would like to give one approach to computing these sorts of expressions involving measures (or other generalised functions) based on epsilon regularisation, which requires a certain amount of geometric computation but which I find to be rather visual and conceptual, compared to more algebraic approaches (e.g. based on Fourier transforms). The idea is to approximate a singular object, such as the singular measure
, by a smoother object
, such as an absolutely continuous measure. For instance, one can approximate
by
where . It is clear that
converges to
in the vague topology, which implies that
converges to
in the vague topology also. Since
,
we will be able to understand the limit f by first considering the function
and then taking (weak) limits as to recover f.
Up to constants, one can compute from elementary geometry that is comparable to
, and
vanishes for
, and is comparable to
for
(and of size
in the transition region
) and is comparable to
for
(and of size about
when
. (This is a good exercise for anyone who wants practice in quickly computing the orders of magnitude of geometric quantities such as areas; for such order of magnitude calculations, quick and dirty geometric methods tend to work better here than the more algebraic calculus methods you would have learned as an undergraduate.) The bounds here are strong enough to allow one to take limits and conclude what f looks like: it is comparable to
. And by being more careful with the computations of area, one can compute the exact formula for f(x), though I will not do so here.
Remark 5. Epsilon regularisation also sheds light on why certain operations on measures or distributions are not permissible. For instance, squaring the Dirac delta function will not give a measure or distribution, because if one looks at the squares
of some smoothed out approximations
to the Dirac function (i.e. approximations to the identity), one sees that their masses go to infinity in the limit
, and so cannot be integrated against test functions uniformly in
. On the other hand, derivatives of the delta function, while no longer measures (the total variation of derivatives of
become unbounded), are at least still distributions (the integrals of derivatives of
against test functions remain convergent).

20 comments
Comments feed for this article
28 February, 2009 at 2:49 am
Harald
In the last paragraph of Example 3 you mean 4 epsilon rather than – 4 epsilon. [Corrected, thanks – T.]
28 February, 2009 at 4:13 am
Dima
In real algebraic geometry the -trick is pushed even further – one works over the field of real Puiseax series
-trick is pushed even further – one works over the field of real Puiseax series  i.e. formal rational-power sums, with the order induced by
i.e. formal rational-power sums, with the order induced by 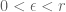 for all
for all  Justifying that the usual real analysis results hold over such a field can be done by Tarski’s transfer argument.
Justifying that the usual real analysis results hold over such a field can be done by Tarski’s transfer argument. is pure (algorithmic, too) algebra. This is all described in great detail in a recent book by S.Basu, R.Pollack, and M.-F.Roy “Algorithms in real algebraic geometry”, that has a free online version.
is pure (algorithmic, too) algebra. This is all described in great detail in a recent book by S.Basu, R.Pollack, and M.-F.Roy “Algorithms in real algebraic geometry”, that has a free online version.
An advantage is that exact computer algebra procedures can work with such objects, and then the final step of taking the limit
28 February, 2009 at 1:36 pm
less than epsilon
Thank you very much Prof. Tao for your wonderful post. I hope that you write some notes on ”generalized functions” and ”weak solutions of PDE”, too. You explain very well and it is very difficult to find such explanations in usuall text books or research papers.
Thanks again…
28 February, 2009 at 1:40 pm
Terence Tao
Dear less than epsilon:
Actually, I happen to have articles on these very topics at
and
I also plan to cover distributions in my class next quarter.
Dear Dima: Thanks for the comment! This trick you mention reminds me of the trick of adjoining a nonstandard infinitesimal to the real number system, and then setting it to zero as a substitute for the usual limit process. Incidentally, the link to download the book you mention seems to not be working right now, but this could be a temporary issue.
to the real number system, and then setting it to zero as a substitute for the usual limit process. Incidentally, the link to download the book you mention seems to not be working right now, but this could be a temporary issue.
28 February, 2009 at 8:46 pm
less than epsilon
Dear Prof. Tao,
I have read your articles on ”distributions” and ” generalized solutions”.
Thank you very much.
I am wondering whether you have written any notes on stochastic partial differential equations. I am working on this field for my Ph.D and it is really very confusing. Adding ”white noise” or ” space-time white noise” in a PDE, namely making the equation stochastic changes the story. But I have not found a nice paper so far on this topic which explains why we are adding noise, what the meaning of ”white noise” or ”space-time white noise” is, what the meaning of the solution is.
I hope you have already some notes on SPDE or one day you write and clarify our mind.
We appreciate your help for math community.
Thanks,
1 March, 2009 at 5:22 am
g
I had problems downloading the book from that page; this page
http://perso.univ-rennes1.fr/marie-francoise.roy/bpr-posted1.html
should work.
1 March, 2009 at 7:37 am
karabasov
Dear less than epsilon,
you may try looking at some of the “classical” books in the field, such as
G. Da Prato and J. Zabczyk, Stochastic equations in infinite dimensions, Cambridge UP 1992
B. Rozovskii, Stochastic evolution systems, Kluwer 1990.
The first book deals with the semigroup approach, the second one with the so-called variational approach (the book treats only linear equations, but the theory works for a rather wide class of nonlinear operators satisfying monotonicity and coercivity conditions).
Both books contain (some) motivation for studying SPDEs, and discuss what one means by “white noise” and “space-time white noise”.
Unfortunately I agree with you that there is a large “industry” that makes a living by taking a deterministic PDE, adding noise to it, and trying to say something about the resulting PDE, without even mentioning why, what for, and so on.
1 March, 2009 at 11:43 am
less than epsilon
Dear Karabasov,
Thank you for your suggestions. Indeed, I had looked at the first book.
Mostly I am looking for a” note” like a survey paper which shows the ”big picture” , addresses the main problems, main approaches, techniques , open problems and further directions.
1 March, 2009 at 1:11 pm
albuquerqueroberta
Very nice post! Thank you !
1 March, 2009 at 8:37 pm
RK
Hi Dr. Tao,
Thanks for the great article.
Small correction: Two paragraphs before “A variant”, the text that appears in square brackets: “It is important to aware” should be “It’s important to be aware”. [Corrected, thanks – T.]
2 March, 2009 at 1:40 am
karabasov
Dear less than epsilon,
unfortunately I do not know anything like that. Frankly speaking, what you are looking for should be provided by your advisor, i.e. he should be able to answer your very legitimate questions! Good luck
2 March, 2009 at 9:21 am
A semana nos arXivs… « Ars Physica
[…] Tricks Wiki: Give yourself an epsilon of room (será que alguém disse mollifier? ) […]
2 March, 2009 at 12:46 pm
nicolaennio
third formula of example one on the left side should not have xi rather than x?
thanks a lot for this clear and useful post
2 March, 2009 at 1:01 pm
Terence Tao
Dear nicolaennio: thanks for the correction!
26 March, 2009 at 7:20 pm
While I’m linking… « Feed The Bears
[…] A post on using statements “up to epsilon” and then letting to prove things. The issue is that sometimes you want to apply machinery to a situation where it doesn’t apply, so you tweak the situation by somehow so the machinery does apply and then let . This is a very standard trick that is even familiar to many undergraduate analysis students. (In opposition to the first two posts, which are more advanced and less prevalent in standard analysis course material.) […]
30 March, 2009 at 8:57 am
245C, Notes 1: Interpolation of L^p spaces « What’s new
[…] remove the assumption that goes to zero at infinity, we use the trick of giving ourselves an epsilon of room. Namely, we multiply by the holomorphic function for some . A little complex arithmetic shows […]
14 November, 2013 at 12:36 pm
Rigorous proofs | Gyre&Gimble
[…] Since for all positive $epsilon$, $f(x)lt f(a)+epsilon$, then $f(x)leq f(a)$. (See also Terry Tao’s article in Tricks […]
21 June, 2016 at 6:12 pm
Anonymous
In Example 1 can one use Schwartz functions instead of the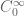 functions?
functions?
Is there any advantage that you use the uncountable family of functions to approximate
to approximate  instead of using a sequence of functions
instead of using a sequence of functions 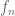 ?
?
22 June, 2016 at 9:11 am
Terence Tao
Yes, there are multiple ways to implement the epsilon of room argument in this case. Whether one uses or
or  as the approximating parameter is mostly a matter of personal taste. I find
as the approximating parameter is mostly a matter of personal taste. I find  to be a more natural parameter here than
to be a more natural parameter here than  (it measures the degree of approximation, whereas
(it measures the degree of approximation, whereas  is just an indexing parameter), but this is a minor aesthetic preference only. Having an uncountable directed set rather than a countable one can occasionally cause some minor technical difficulties, but these can usually be resolved by passing to a countable subset (e.g. restricting to
is just an indexing parameter), but this is a minor aesthetic preference only. Having an uncountable directed set rather than a countable one can occasionally cause some minor technical difficulties, but these can usually be resolved by passing to a countable subset (e.g. restricting to  s of the form
s of the form  for some natural number
for some natural number  ) whenever needed.
) whenever needed.
23 January, 2021 at 12:56 pm
246B, Notes 2: Some connections with the Fourier transform | What's new
[…] remove the assumption that goes to zero at infinity, we use the trick of giving ourselves an epsilon of room. Namely, we multiply by the holomorphic function for some . A little complex arithmetic shows […]