The celebrated Szemerédi-Trotter theorem gives a bound for the set of incidences between a finite set of points
and a finite set of lines
in the Euclidean plane
. Specifically, the bound is
where we use the asymptotic notation or
to denote the statement that
for some absolute constant
. In particular, the number of incidences between
points and
lines is
. This bound is sharp; consider for instance the discrete box
with
being the collection of lines
. One easily verifies that
,
, and
, showing that (1) is essentially sharp in the case
; one can concoct similar examples for other regimes of
and
.
On the other hand, if one replaces the Euclidean plane by a finite field geometry
, where
is a finite field, then the estimate (1) is false. For instance, if
is the entire plane
, and
is the set of all lines in
, then
are both comparable to
, but
is comparable to
, thus violating (1) when
is large. Thus any proof of the Szemerédi-Trotter theorem must use a special property of the Euclidean plane which is not enjoyed by finite field geometries. In particular, this strongly suggests that one cannot rely purely on algebra and combinatorics to prove (1); one must also use some Euclidean geometry or topology as well.
Nowadays, the slickest proof of the Szemerédi-Trotter theorem is via the crossing number inequality (as discussed in this previous post), which ultimately relies on Euler’s famous formula ; thus in this argument it is topology which is the feature of Euclidean space which one is exploiting, and which is not present in the finite field setting. Today, though, I would like to mention a different proof (closer in spirit to the original proof of Szemerédi-Trotter, and also a later argument of Clarkson et al.), based on the method of cell decomposition, which has proven to be a very flexible method in combinatorial incidence geometry. Here, the distinctive feature of Euclidean geometry one is exploiting is convexity, which again has no finite field analogue.
Roughly speaking, the idea is this. Using nothing more than the axiom that two points determine at most one line, one can obtain the bound
which is inferior to (1). (On the other hand, this estimate works in both Euclidean and finite field geometries, and is sharp in the latter case, as shown by the example given earlier.) Dually, the axiom that two lines determine at most one point gives the bound
(or alternatively, one can use projective duality to interchange points and lines and deduce (3) from (2)).
An inspection of the proof of (2) shows that it is only expected to be sharp when the bushes associated to each point
behave like “independent” subsets of
, so that there is no significant correlation between the bush
of one point and the bush of another point
.
However, in Euclidean space, we have the phenomenon that the bush of a point is influenced by the region of space that
lies in. Clearly, if
lies in a set
(e.g. a convex polygon), then the only lines
that can contribute to
are those lines which pass through
. If
is a small convex region of space, one expects only a fraction of the lines in
to actually pass through
. As such, if
and
both lie in
, then
and
are compressed inside a smaller subset of
, namely the set of lines passing through
, and so should be more likely to intersect than if they were independent. This should lead to an improvement to (2) (and indeed, as we shall see below, ultimately leads to (1)).
More formally, the argument proceeds by applying the following lemma:
Lemma 1 (Cell decomposition) Let
be a finite collection of lines in
, let
be a finite set of points, and let
. Then it is possible to find a set
of
lines in
, plus some additional open line segments not containing any point in
, which subdivide
into
convex regions (or cells), such that the interior of each such cell is incident to at most
lines.
The deduction of (1) from (2), (3) and Lemma 1 is very quick. Firstly we may assume we are in the range
otherwise the bound (1) follows already from either (2) or (3) and some high-school algebra.
Let be a parameter to be optimised later. We apply the cell decomposition to subdivide
into
open convex regions, plus a family
of
lines. Each of the
convex regions
has only
lines through it, and so by (2) contributes
incidences. Meanwhile, on each of the lines
in
used to perform this decomposition, there are at most
transverse incidences (because each line in
distinct from
can intersect
at most once), plus all the incidences along
itself. Putting all this together, one obtains
We optimise this by selecting ; from (4) we can ensure that
, so that
. One then obtains
We can iterate away the error (halving the number of lines each time) and sum the resulting geometric series to obtain (1).
It remains to prove (1). If one subdivides using
arbitrary lines, one creates at most
cells (because each new line intersects the existing lines at most once, and so can create at most
distinct cells), and for a similar reason, every line in
visits at most
of these regions, and so by double counting one expects
lines per cell “on the average”. The key difficulty is then to get
lines through every cell, not just on the average. It turns out that a probabilistic argument will almost work, but with a logarithmic loss (thus having
lines per cell rather than
); but with a little more work one can then iterate away this loss also. The arguments here are loosely based on those of Clarkson et al.; a related (deterministic) decomposition also appears in the original paper of Szemerédi and Trotter. But I wish to focus here on the probabilistic approach.)
It is also worth noting that the original (somewhat complicated) argument of Szemerédi-Trotter has been adapted to establish the analogue of (1) in the complex plane by Toth, while the other known proofs of Szemerédi-Trotter, so far, have not been able to be extended to this setting (the Euler characteristic argument clearly breaks down, as does any proof based on using lines to divide planes into half-spaces). So all three proofs have their advantages and disadvantages.
— 1. The trivial incidence estimate —
We first give a quick proof of the trivial incidence bound (2). We have
and thus by Cauchy-Schwarz
On the other hand, observe that
Because two distinct points are incident to at most one line, the right-hand side is at most
, thus
Comparing this with the Cauchy-Schwarz bound and using a little high-school algebra we obtain (2). A dual argument (swapping the role of lines and points) give (3).
A more informal proof of (2) can be given as follows. Suppose for contradiction that was much larger than
. Since
, this implies that that the
are much larger than
on the average. By the birthday paradox, one then expects two randomly chosen
to intersect in at least two places
; but this would mean that two lines intersect in two points, a contradiction. The use of Cauchy-Schwarz in the rigorous argument given above can thus be viewed as an assertion that the average intersection of
and
is at least as large as what random chance predicts.
As mentioned in the introduction, we now see (intuitively, at least) that if nearby are such that
are drawn from a smaller pool of lines than
, then their intersection is likely to be higher, and so one should be able to improve upon (2).
— 2. The probabilistic bound —
Now we start proving Lemma 1. We can assume that , since the claim is trivial otherwise (we just use all the lines in
to subdivide the plane, and there are no lines left in
to intersect any of the cells). Similarly we may assume that
, and that
is large. We can also perturb all the lines slightly and assume that the lines are in general position (no three are concurrent), as the general claim then follows from a limiting argument (note that this may send some of the cells to become empty). (Of course, the Szemerédi-Trotter theorem is quite easy under the assumption of general position, but this theorem is not our current objective right now.)
We use the probabilistic method, i.e. we construct by some random recipe and aim to show that the conclusion of the lemma holds with positive probaility.
The most obvious approach would be to choose the lines
at random from
, thus each line
has a probability of
of lying in
. Actually, for technical reasons it is slightly better to use a Bernoulli process to select
, thus each line
lies in
with an independent probability of
. This can cause
to occasionally have size much larger than
, but this probability can be easily controlled (e.g. using the Chernoff inequality). So with high probability,
consists of
lines, which therefore carve out
cells. The remaining task is to show that each cell is incident to at most
lines from
.
Observe that each cell is a (possibly unbounded) polygon, whose edges come from lines in . Note that (except in the degenerate case when
consists of at most one line, which we can ignore) any line
which meets a cell in
, must intersect at least one of the edges of
. If we pretend for the moment that all cells have a bounded number of edges, it would then suffice to show that each edge of each cell was incident to
lines.
Let’s see how this would go. Suppose that one line was picked for the set
, and consider all the other lines in
that intersect
; there are
of these lines
, which (by the general position hypothesis) intersect
at distinct points
on the line. If one of these lines
intersecting
is also selected for
, then the corresponding point
will become a vertex of one of the cells (indeed, it will be the vertex of four cells). Thus each of these points on
has an independent probability of
of becoming a vertex for a cell.
Now consider consecutive such points on
. The probability that they all fail to be chosen as cell vertices is
; if
, then this probability is
. Thus runs of much more than
points without vertices are unlikely. In particular, setting
, we see that the probability that any given
consecutive points on any given line
are skipped is
. By the union bound, we thus see that with probability
, that every line
has at most
points between any two adjacent vertices. Or in other words, the edge of every cell is incident to at most
lines from
. This yields Lemma 1 except for two things: firstly, the logarthmic loss of
, and secondly, the assumption that each cell had only a bounded number of edges.
To fix the latter problem, we will have to add some line segments to . First, we randomly rotate the plane so that none of the lines in
are vertical. Then we do the following modified construction: we select
lines from
as before, creating
cells, some of which may have a very large number of edges. But then for each cell, and each vertex in that cell, we draw a vertical line segment from that vertex (in either the up or down direction) to bisect the cell into two pieces. (If the vertex is on the far left or far right of the cell, we do nothing.) Note that almost surely this construction will avoid hitting any point in
. Doing this once for each vertex, we see that we have subdivided each of the old cells into a number of new cells, each of which have at most four sides (two vertical sides, and two non-vertical sides). So we have now achieved a bounded number of sides per cell. But what about the number of such cells? Well, each vertex of each cell is responsible for at most two subdivisions of one cell into two, and the number of such vertices is at most
(as they are formed by intersecting two lines from the original selection of
lines together), so the total number of cells is still
.
Is it still true that each edge of each cell is incident to lines in
? We have already proven this (with high probability) for all the old edges – the ones that were formed from lines in
. But there are now some new edges, caused by dropping a vertical line segment from the intersection of two lines in
. But it is not hard to see that one can use much the same argument as before to see that with high probability, each of these line segments is incident to at most
lines in
as desired.
Finally, we have to get rid of the logarithm. An inspection of the above arguments (and a use of the first moment method) reveals the following refinement: for any , there are expected to be at most
cells which are incident to more than
lines, where
is an absolute constant. This is already enough to improve the
bound slightly to
. But one can do even better by using Lemma 1 as an induction hypothesis, i.e. assume that for any smaller set
of lines with
, and any
, one can partition
into at most
cells using at most
lines such that each cell is incident to at most
lines, where
are absolute constants. (When using induction, asymptotic notation becomes quite dangerous to use, and it is much safer to start writing out the constants explicitly. To close the induction, one has to end up with the same constants
as one started with.) For each
between
and
which is a power of two, one can apply the induction hypothesis to all the cells which are incident to between
and
(with
set equal to the lines in
incident to this cell, and
set comparable to
), and sum up (using the fact that
converges, especially if
is restricted to powers of two) to close the induction if the constants
are chosen properly; we leave the details as an exercise.

24 comments
Comments feed for this article
13 June, 2009 at 12:06 pm
JSE
Is there at this point any proof of Szemeredi-Trotter via something like the polynomal method? This “Algebraic Methods…” paper of Guth and Katz is at least one instance where the method gives you some new insight into problems about the combinatorics of incidences.
13 June, 2009 at 12:36 pm
Terence Tao
I certainly think so! For one thing, there is a link between Szemeredi-Trotter and sum-product theorems (this is discussed in my crossing number article), so having a new approach to Szemeredi-Trotter, such as a polynomial approach, may well lead to new sum-product theorems, which is certainly of interest. Also, the current proof of Szemeredi-Trotter in the complex plane is rather messy; a clean proof would be good. Finally, the F_p Szemeredi-Trotter paper in my paper with Bourgain and Katz is only an epsilon better than trivial, and only applies to situations in which the number of lines and points is the same; improving either of these would be desirable (I understand that removing the latter would be helpful for some of the SL_d(F_p) product estimates).
There is also the problem of getting a good inverse theorem, i.e. when is Szemeredi-Trotter close to sharp? It’s unlikely that the polynomial method would help with that specific question, but having some other proof of Szemeredi-Trotter could also be useful for this purpose.
Finally, developing the polynomial method for its own sake seems worthwhile – it looks like an approach with a lot of potential for other combinatorial incidence geometry problems.
13 June, 2009 at 1:59 pm
JSE
You “certainly think so” meaning such a proof is already known, or that it would be good if it were? I’m wholeheartedly with you on the latter.
13 June, 2009 at 8:13 pm
Terence Tao
Ah, I misread your “Is there at this point any” as “Is there any point to have a” :-). No, I don’t know of such an argument, but I would love to hear of one.
13 June, 2009 at 10:10 pm
jozsef
Dear Terry. I think that the cutting lemma proof – which you presented here – tells us more about the structure of point-line arrangements with almost maximal number of incidences. Let me give an example. In your calculations you count lines being incident to two points in a cell it crosses. If the number of incidences is close to the Szemeredi-Trotter bound then using a cell decomposition one can guarantee that a typical line is incident to at least 3 points in a cell. Then a typical cell which has points has about
points has about  many collinear triples. Then, by Ruzsa-Szemeredi, it contains many (
many collinear triples. Then, by Ruzsa-Szemeredi, it contains many ( ) triangles. So, one can see that if an arrangement has many incidences then it contains many triangles.
) triangles. So, one can see that if an arrangement has many incidences then it contains many triangles.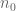 that if
that if  and the number of incidences between a set of n points, P, and a set of n lines, L, is at least
and the number of incidences between a set of n points, P, and a set of n lines, L, is at least  then there is a triangle, (i.e. three lines from L that the three crossing points are in P.)
then there is a triangle, (i.e. three lines from L that the three crossing points are in P.)
It would be nice to see a simple geometric proof for this; show (without using Ruzsa-Szemeredi) that for every positive c there is threshold
About Csaba Toth’s paper on the complex case; As far as I know the manuscript has been at COMBINATORICA for more than 8 years(!) without a final decision. I believe that Csaba’s result is correct, however it might be difficult to referee.
14 June, 2009 at 2:35 am
iosevich
Are there any recent results in the direction of improving Szemeredi-Trotter for points and circles of the same radius?
14 June, 2009 at 8:29 am
JSE
As far as I know the manuscript has been at COMBINATORICA for more than 8 years(!) without a final decision.
Time for the Polyreferee Project?
19 June, 2009 at 12:38 pm
E. Mehmet Kıral
Dear Professor Tao,
I fail to see how you could conclude that the proof of Szemeredi-Trotter theorem must essentially use some sort of topological or convexity argument from the finite field example you gave above.
The Szemeredi-Trotter theorem given above involves an asymptotic inequality on the number of points and lines. However in the finite plane these are bounded and by choosing the hidden constant sufficiently large, we may let the inequality be satisfied.
Or is there some reason to believe that a generalization of Szemeredi-Trotter theorem to finite fields must involve a constant that is independent of the field (or maybe only dependent on the characteristic)?
Perhaps by observing that this result does not hold in “infinite characteristic p” fields, or maybe in fields with a quite different topology such as the p-adics we may deduce that the convexity arguments were necessary. Maybe it does.
Best Regards,
19 June, 2009 at 1:47 pm
Terence Tao
Dear Mehmet,
Well, if a proof of Szemeredi-Trotter did not use anything special about the ambient field, such as topology or convexity, then it would apply uniformly for all fields, and the finite field examples show that this is not the case; one cannot make the implied constant C the same for every choice of finite field, though of course as you say one can trivially find a C for any fixed choice of finite field for which Szemeredi-Trotter holds.
Also, it is not difficult to pack a lot of finite field examples (with the same characteristic) into an infinite field example. Consider for instance the algebraic closure of a finite field. This contains arbitrary large finite subfields G, just take any finite extension of F. For each such subfield G, one can create a Szemeredi-Trotter counterexample in the plane
of a finite field. This contains arbitrary large finite subfields G, just take any finite extension of F. For each such subfield G, one can create a Szemeredi-Trotter counterexample in the plane  and hence in the plane
and hence in the plane  by the construction in the post; thus Szemeredi-Trotter fails (for any choice of constant) for the field
by the construction in the post; thus Szemeredi-Trotter fails (for any choice of constant) for the field  . Thus any proof of Szemeredi-Trotter must use some property of the real line which is not shared by
. Thus any proof of Szemeredi-Trotter must use some property of the real line which is not shared by  , which seems to rule out most of the purely algebraic approaches to the problem, and is consistent with the fact that all known proofs use either topological or convexity methods.
, which seems to rule out most of the purely algebraic approaches to the problem, and is consistent with the fact that all known proofs use either topological or convexity methods.
[Actually, there is a loophole here. There is known to be a link between Szemeredi-Trotter theorems and sum-product theorems. The latter can be established by algebraic (and combinatorial) means, the main ingredient being a hypothesis that the ambient field contains no finite subfields, a statement which does indeed distinguish the real line from examples such as ; this is done for instance in my book with Van Vu. It is also known that sum-product theorems can yield some non-trivial results of Szemeredi-Trotter type (see e.g. my paper with Bourgain and Katz) but there is no known way of using this technology to establish the full Szemeredi-Trotter theorem.]
; this is done for instance in my book with Van Vu. It is also known that sum-product theorems can yield some non-trivial results of Szemeredi-Trotter type (see e.g. my paper with Bourgain and Katz) but there is no known way of using this technology to establish the full Szemeredi-Trotter theorem.]
24 June, 2009 at 6:51 am
Points and lines « Konrad Swanepoel’s blog
[…] June 2009 in Discrete Geometry Terry Tao has a great post about the Szemeredi-Trotter theorem on the maximum number of incidences between m points and n […]
20 November, 2010 at 1:11 pm
The Guth-Katz bound on the Erdős distance problem « What’s new
[…] number methods (as discussed in this previous blog post) or by cell decomposition (as discussed in this previous blog post). In both cases, the order structure of (and in particular, the fact that a line divides a plane […]
18 February, 2011 at 6:41 am
The Szemeredi-Trotter theorem via the polynomial ham sandwich theorem « What’s new
[…] (as discussed in this previous post) or via a slightly different type of cell decomposition (as discussed here). The proof given below is not that different, in particular, from the latter proof, but I believe […]
20 March, 2011 at 8:47 am
Taole Zhu
Does the cell decomposition lemma have a multidimensional analogue?
20 March, 2011 at 3:22 pm
Terence Tao
Yes. See for instance
8 February, 2012 at 6:17 am
iitdelhireport
Dear Terry, I know I am almost three years late to notice, but why can we guarantee that the cardinality of R is O(r)? My problem is that in your proof we might add r^2 vertical segments when we “fix the latter problem”.
At other places (e.g. Matousek’s book) it is only claimed that the number of cells is O(r^2). I wonder if this stronger version also holds.
8 February, 2012 at 8:05 am
Terence Tao
Well, the only reason we needed R have cardinality O(r) is so that we have only O(r^2) cells, and we keep that latter property when the vertical line segments are added, so the cardinality of the modified R is no longer relevant. (I guess it would be more precise to say that we are not modifying R, but rather modifying how the cells are constructed from R.)
8 February, 2012 at 9:04 am
iitdelhireport
Thank you for your fast reply. I agree with you completely but in this case Lemma 1 is quite misunderstandable as you stated it in the post. It suggests that the cells are derived by partitioning the plane by r lines, which is not the case.
8 February, 2012 at 9:27 am
Terence Tao
Ah, a fair point; I’ve reworded the text accordingly.
9 February, 2012 at 9:50 pm
Mistery solved! « iitdelhireport
[…] https://terrytao.wordpress.com/2009/06/12/the-szemeredi-trotter-theorem-and-the-cell-decomposition/#c… Share this:TwitterFacebookLike this:LikeBe the first to like this post. […]
14 July, 2012 at 5:30 am
Is the cutting lemma true with O(r) lines? | Q&A System
[…] The cutting lemma (a.k.a. cell decomposition lemma) states that given $n$ lines within the plane you’ll be able to divide it into $O(r^2)$ regions (even triangles) for just about any $1le rle n$ so that the inside associated with a region is intersected by $O(n/r)$ lines. For additional see e.g. Matousek’s book Lectures on Discrete Geometry or this publish. […]
20 April, 2013 at 5:48 pm
Is the cutting lemma true with O(r) lines? | Question and Answer
[…] The cutting lemma (a.k.a. cell decomposition lemma) states that given $n$ lines in the plane it is possible to divide it into $O(r^2)$ regions (even triangles) for any $1le rle n$ such that the interior of any region is intersected by $O(n/r)$ lines. For more see e.g. Matousek’s book Lectures on Discrete Geometry or this post. […]
26 September, 2016 at 7:43 am
Incidence Bounds and Interlacing Eigenvalues | Anurag's Math Blog
[…] some constant . This result can be proved in several ways (including polynomial method), all of which use some topological property of the real plane. The same result does not hold over […]
4 October, 2022 at 3:43 pm
Natalie Behague
Hello! I have a question about the induction step at the end. I believe you are saying that for each ‘bad’ cell with more than C|L|/r lines intersecting it, we add to the set R the lines R’ given by the induction hypothesis, where L’ is the set of lines intersecting this cell.
For k a power of 2 say a cell has ‘badness’ k if it has between k C|L|/r and 2k C|L|/r lines intersecting it. The number of cells with badness k is about r^2e^{-k}. So in total we add about sum(r^2 e^{-k} 2Ck) new lines, summing over k being all powers of 2. This is O(r^2) lines added. Isn’t this too many? Have I misunderstood the inductive step?
Thank you!
4 October, 2022 at 8:38 pm
Terence Tao
Hmm, you’re right, the inductive argument does not close as stated. One can omit this induction and just settle for a weaker lemma in which one allows, for each , to have a small number (
, to have a small number ( 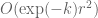 or so) cells in which one has as many as
or so) cells in which one has as many as  lines per cell, and this is still good enough for most applications. (Looking back at the Clarkson et al. paper, I now see that they also only control incidences per cell on the average, although they do cite other results of Chazelle-Friedman and Matousek that get the uniformity by a more complicated argument.)
lines per cell, and this is still good enough for most applications. (Looking back at the Clarkson et al. paper, I now see that they also only control incidences per cell on the average, although they do cite other results of Chazelle-Friedman and Matousek that get the uniformity by a more complicated argument.)